基于深度神經網(wǎng)絡的橫流轉捩預測1)

胡震宇 王子路 陳堅強 袁先旭 向星皓

(空氣動力學國家重點實驗室,四川綿陽 621000)

引言

轉捩是一個連續(xù)演化的流動過程,是一種從簡單分層穩(wěn)定狀態(tài)向復雜多變湍流狀態(tài)的過渡[1].轉捩研究不僅具有重要的理論意義,還具有重要的工程應用價值.轉捩過程受多種模態(tài)影響[2],由于其復雜性,將長期作為現(xiàn)代流體力學重點關注的前沿領域而存在[3].

關于流體力學的研究,飛行試驗、地面實驗具有直觀、真實的特點,能夠為穩(wěn)定性理論、數(shù)值計算提供較為準確的驗證數(shù)據(jù)[4-6].直接數(shù)值模擬(direct numerical simulation,DNS)方法[7-10]直接求解N-S 方程,能夠準確捕捉流場結構,但對計算資源要求較高;大渦模擬(large eddy simulation,LES)方法[11]對大尺度渦進行解析、對小尺度渦進行模化,計算結果較為準確,但依然要求較高的網(wǎng)格分辨率;雷諾平均N-S (Reynolds averaged Navier-Stokes,RANS)方法[12-14]中,利用湍流模型封閉雷諾應力項,降低了對網(wǎng)格分辨率的要求,應用較為廣泛.

基于RANS 方法的k-ε,k-ω,SSTk-ω等傳統(tǒng)湍流模型,能夠一定程度上滿足工程需要,但無法捕捉邊界層內轉捩的過程.對于轉捩過程的描述,通常用到間歇因子γ[15]

式中,I(x,y,z,t)表征某一空間點在某一時刻的流動狀態(tài),處于湍流狀態(tài)時I(x,y,z,t)=1,處于層流狀態(tài)時I(x,y,z,t)=0.

間歇因子γ表征某一空間點處于湍流狀態(tài)的時間占總時間T的比例.通過求解間歇因子γ的輸運方程,可以獲得間歇因子γ在流場中的分布情況.轉捩模型通過對間歇因子γ或其他參數(shù)進行建模,并與湍流模型耦合求解,實現(xiàn)對轉捩過程的預測.

Steelant 等[15]針對bypass 轉捩,構建了間歇因子γ的輸運方程,計算結果能夠與實驗數(shù)據(jù)較好地吻合.目前應用較廣的轉捩模型,也是通過構建間歇因子γ的輸運方程來實現(xiàn)轉捩預測的.例如Langtry等[16]建立的γ-Reθ轉捩模型,王亮等[17]建立的k-ω-γ轉捩模型.

神經網(wǎng)絡通過模仿生物的大腦神經元結構和功能,使計算機對數(shù)據(jù)信息能夠進行智能處理,構建復雜、非線性映射關系[18].相比于求解輸運方程,深度神經網(wǎng)絡(deep neural networks,DNN)所需的計算資源更少,顯著提高計算效率,在湍流模型化工作中具有良好的前景[19-20].

Templeton 等[21]提出了張量基神經網(wǎng)絡 (tensor based neural network,TBNN) 架構,并用于預測低速的管流、周期山流動.任海杰等[22]基于文獻[21]搭建的 TBNN 內核構建了神經網(wǎng)絡模型,并針對Boussinesq 假設難以準確捕捉雷諾應力各向異性張量的問題,利用Pope[23]給出的各向異性張量b與基張量T(n)之間的本構關系,構建了張量不變量λ1～λ5與標量函數(shù)g(n)間的映射關系,對高超聲速平板進行預測,得到的各向異性張量分布與DNS 計算結果吻合較好.Wei 等[24]提出了基于深度強化學習的流體力學微分方程統(tǒng)一求解框架,求解了流體力學Burgers 方程、穩(wěn)態(tài)N-S 方程.Sekar 等[25]基于深度學習方法,針對具有不同外形的機翼,構建了繞流流場預測模型.Zhu 等[26]通過徑向基函數(shù)神經網(wǎng)絡以及深度神經網(wǎng)絡,對渦黏系數(shù)進行了預測,并用于封閉湍流模型.張珍等[27]提出了一種基于組合神經網(wǎng)絡預測渦黏系數(shù)和雷諾應力各向異性張量的修正方法,對雷諾應力的線性部分進行了求解.Beetham等[28]運用傳統(tǒng) RANS 方法求解RANS 模型線性部分,運用神經網(wǎng)絡預測RANS 模型非線性部分,但缺乏足夠精度.

目前人工智能在計算流體力學領域的研究,主要集中在重構或修正湍流渦黏性和雷諾應力[29].隨著學科間的交叉與發(fā)展,將神經網(wǎng)絡應用于邊界層轉捩問題求解,成為一個新的熱門研究方向.鄭天韻等[29]基于深度殘差網(wǎng)絡(deep residual network,ResNet),構建了間歇因子γ與流場平均量間的映射關系,并與spallart allmaras (SA)湍流模型耦合,發(fā)展了一種類代數(shù)轉捩模型,性能接近SST-γ-Reθ模型,但收斂到同一精度節(jié)省了超過30% 的計算成本.Foroozan 等[30]運用Johns Hopkins 湍流數(shù)據(jù)庫(Johns Hopkins turbulence databases,JHTDB)構建了訓練數(shù)據(jù)集,采用無監(jiān)督機器學習的方法,實現(xiàn)了對邊界層bypass 轉捩的識別.

本文DNN 基于Pytorch 平臺.數(shù)值計算基于Chant 2.0 平臺[31-32],該平臺部署了橫流拓展γ-Reθ轉捩模型[33].橫流拓展γ-Reθ轉捩模型在原始γ-Reθ轉捩模型[16]上進行改進,在NLF(2)-0415 后掠翼、6 : 1 標準橢球體、鐮刀翼和DLR-F4 翼身組合體等典型橫流轉捩算例上均有著良好的計算效果,能做到與實驗數(shù)據(jù)極大程度吻合[34-35].后文直接使用γ-Reθ轉捩模型,代指部署于Chant 2.0 平臺的橫流拓展γ-Reθ轉捩模型.

本文運用γ-Reθ轉捩模型對橫流轉捩模態(tài)下間歇因子γ的數(shù)值與分布進行計算,并對DNN 進行監(jiān)督學習,構建從層流流場物理量到轉捩流場間歇因子γ間的映射關系,從而得到一種新的數(shù)據(jù)驅動轉捩模型.僅需將數(shù)據(jù)驅動轉捩模型與SSTk-ω湍流模型耦合,即可對橫流不穩(wěn)定性主導的邊界層轉捩進行預測,簡化計算過程.

本文采用數(shù)據(jù)驅動轉捩模型與湍流模型耦合求解的手段,研究了人工智能轉捩計算方法對橫流轉捩的預測能力,以期為今后的人工智能算法與CFD耦合工作提供方法參考.

1 模型構建

1.1 DNN 監(jiān)督學習框架

本文參照γ-Reθ轉捩模型求解間歇因子γ,修正SSTk-ω模型湍動能k輸運方程的生成項與耗散項,進而實現(xiàn)轉捩預測的思路,利用DNN 構建來流條件、壁面信息和流場結構等物理信息與間歇因子γ間的映射關系,用新的數(shù)據(jù)驅動轉捩模型替代γ-Reθ轉捩模型,實現(xiàn)人工智能建模框架下的三維邊界層橫流轉捩的高效準確預測.

目前已有許多基于層流解的邊界層轉捩研究工作[36-39].以本文所用的γ-Reθ轉捩模型構造為例,在發(fā)生轉捩前流場處于全層流狀態(tài),通過迭代層流流場的物理量從而開啟橫流源項DSCF實現(xiàn)轉捩預測,即層流流場中存在能夠用于判斷橫流轉捩起始位置的點.因此本文選擇使用層流流場物理量映射轉捩流場間歇因子,訓練數(shù)據(jù)的具體獲取方式如下.首先對層流狀態(tài)進行計算,快速得到收斂穩(wěn)定的層流流場,并提取訓練所需的物理量.再通過SSTk-ω湍流模型與γ-Reθ轉捩模型計算轉捩流場,提取各個流場點對應的γ值.將γ與上一步提取的層流流場物理量進行匹配,用于監(jiān)督學習.DNN 通過梯度下降法,計算γ預測值與監(jiān)督學習的γ真實值(即γ-Reθ轉捩模型計算得到的γ值)之間的損失函數(shù),并對DNN各節(jié)點的超參數(shù)進行修正,使損失函數(shù)降低至設定值以下,從而獲得能夠滿足轉捩計算精度要求的映射關系,該映射關系即為本研究的數(shù)據(jù)驅動轉捩模型.DNN 監(jiān)督學習功能實現(xiàn)的具體過程見圖1.

1.2 湍流與轉捩模型

本文以RANS 方程對變雷諾數(shù)、變后掠角的NFL(2)-0415 后掠翼以及6 : 1 標準橢球體進行求解,采用兩方程的剪切應力輸運SSTk-ω湍流模型,并與γ-Reθ轉捩模型耦合.γ-Reθ轉捩模型由間歇因子γ輸運方程、轉捩動量厚度雷諾數(shù)輸運方程構成,具體構造如下

橫流轉捩源項的常系數(shù)CCF參照文獻[35]的研究結果取0.2,其余常系數(shù)、參數(shù)與文獻[34]保持一致.

γ-Reθ模型與SSTk-ω湍流模型的耦合,通過有效間歇因子γeff對湍動能k方程生成項和耗散項修正實現(xiàn).SSTk-ω湍流模型的湍動能k方程被修改為

SSTk-ω湍流模型中的融合函數(shù)F1也需要修改

式中,Pk,Dk和Florig均為SSTk-ω湍流模型的原始形式[40].

1.3 模型計算能力驗證

本文利用γ-Reθ轉捩模型對間歇因子γ進行計算,并將計算結果作為γ真實值進行監(jiān)督學習,參與DNN 訓練與測試.得到的數(shù)據(jù)驅動轉捩模型與SSTk-ω湍流模型耦合,用于預測變后掠角的NFL(2)-0415 后掠翼、6 : 1 標準橢球體的三維邊界層橫流轉捩.首先需要對γ-Reθ模型性能進行校驗,以證明其計算結果的可靠性.

NFL(2)-0415 后掠翼在?4°攻角(attract of angle,AoA)、45°后掠角(sweep angle,Λ)下[41],上翼面的轉捩由橫流不穩(wěn)定性主導,是低速橫流轉捩典型算例[42].選取該算例,運用γ-Reθ轉捩模型對變雷諾數(shù)的NFL(2)-0415 后掠翼上翼面轉捩位置進行預測,并將計算所得的γ分布與層流流場物理量進行匹配,參與DNN 的訓練、測試.具體計算工況見表1.

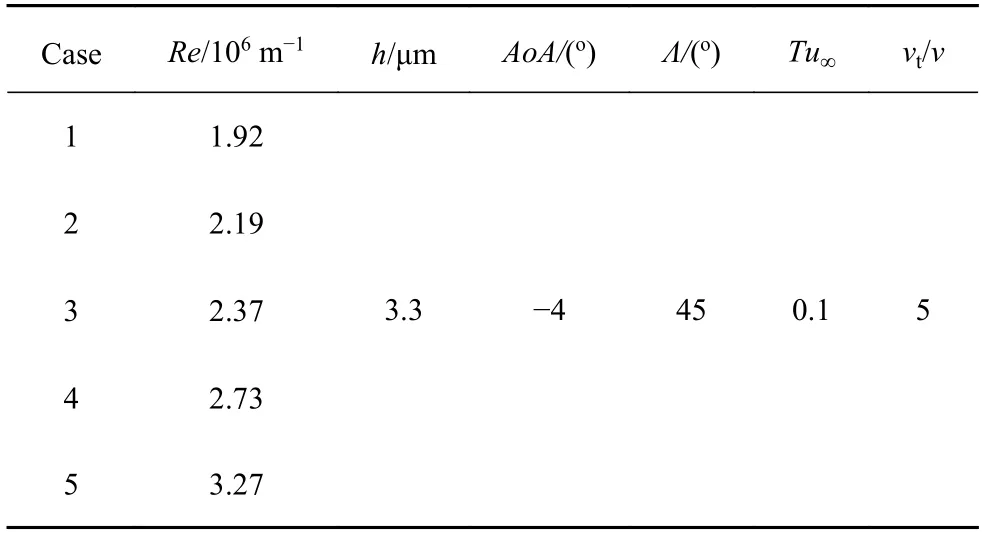
表1 NFL(2)-0415 后掠翼計算條件Table 1 Conditions of NFL(2)-0415 airfoil

如圖2 所示,C 型結構化網(wǎng)格流向i共有400 網(wǎng)格點,其中上、下翼面、上、下尾跡各分布100 網(wǎng)格點,網(wǎng)格法向j共有151 網(wǎng)格點,第1 層網(wǎng)格法向間距y+<1,網(wǎng)格展向k為二層網(wǎng)格,網(wǎng)格數(shù)量為120 800.計算采用周期邊界條件,以實現(xiàn)無線展長后掠翼的數(shù)值模擬.網(wǎng)格在邊界層內及邊界層附近保證了良好的正交性,粗黑曲線與壁面間的網(wǎng)格點數(shù)據(jù)用于神經網(wǎng)絡的訓練.

圖2 NLF(2)-0415 后掠翼計算網(wǎng)格Fig.2 Computing mesh for NLF(2)-0415 airfoil

本文采用層流區(qū)域與轉捩區(qū)域Cf曲線延長線交點的無量綱化坐標x/c作為轉捩位置xtr,如圖3所示.圖4 給出了本研究γ-Reθ轉捩模型的計算結果與實驗結果[41]、langtry-menter-CFH 模型[42]計算結果對比.

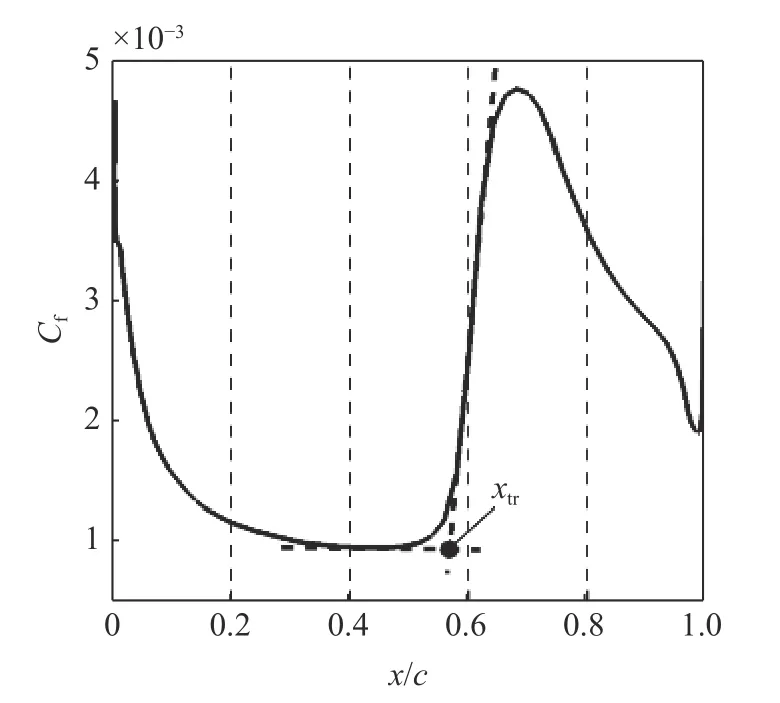
圖3 轉捩位置判定Fig.3 Determination of transition location

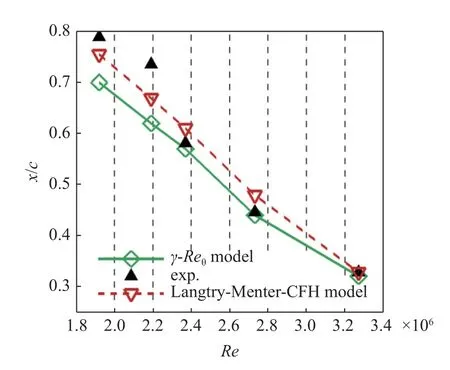
圖4 轉捩位置對比Fig.4 Comparison of transition location

由圖4 可知,γ-Reθ轉捩模型計算轉捩位置xtr在各工況下均小幅度先于Langtry-Menter-CFH 模型.γ-Reθ轉捩模型在低雷諾數(shù)下,計算轉捩位置xtr相較于實驗結果略微提前,隨著雷諾數(shù)增大,計算轉捩位置xtr逐漸與實驗結果貼近,最后幾乎重合.Langtry-Menter-CFH 模型在低雷諾數(shù)下計算轉捩位置xtr同樣存在略微提前的問題,隨著雷諾數(shù)增大,計算轉捩位置xtr出現(xiàn)滯后,雷諾數(shù)繼續(xù)增大,計算轉捩位置xtr逐漸與實驗結果貼近并重合.

轉捩模型計算結果與實驗結果間的差異,與模型本身構建、模型中部分參數(shù)的標定等諸多因素有關,且不同研究中轉捩點坐標xtr的判定方式同樣存在區(qū)別.盡管存在以上影響,γ-Reθ轉捩模型計算結果依然能與實驗數(shù)據(jù)吻合較好,與Langtry-Menter-CFH 模型具有相仿的計算性能,能夠滿足預測精度和DNN 訓練的需求.

2 深度神經網(wǎng)絡

2.1 深度神經網(wǎng)絡超參數(shù)

DNN 的輸入層為選定的層流流場物理量,并用γ-Reθ模型計算得到的間歇因子γ進行監(jiān)督學習.輸入層單個樣本的特征量為V[0]=(v1,v2,v3,···,vn),經過隱藏層時,在神經元節(jié)點經歷線性變換與激活函數(shù)的非線性變化,并將輸出值作為下一隱藏層的輸入,直至輸出最終結果,如圖5 所示.其中上角標[j]表示第j個隱藏層,下角標i表示該隱藏層的第i個神經節(jié)點.

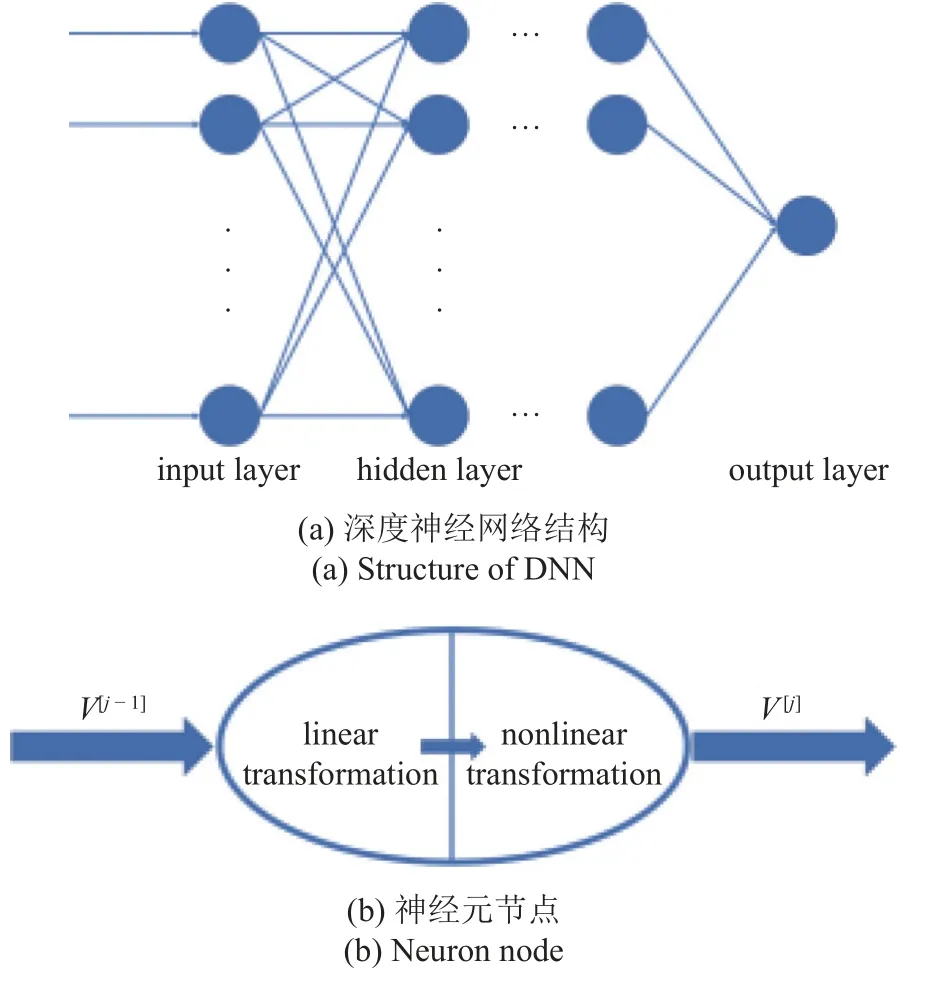
圖5 深度神經網(wǎng)絡正向傳播Fig.5 Positive propagation of DNN

訓練樣本集中的單個樣本首先經過如下線性變換與非線性變換

經測試,在本研究中選取sigmoid 函數(shù)作為激活函數(shù)學習效果比ReLU 函數(shù)、tanh 函數(shù)更佳.非線性變換過程中的激活函數(shù)σ選取sigmoid 函數(shù),函數(shù)曲線如圖6 所示,定義如下

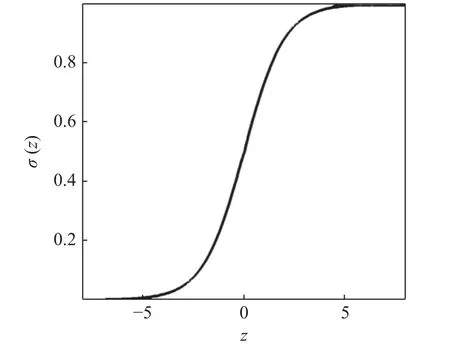
圖6 Sigmoid 函數(shù)Fig.6 Activation function of sigmoid

對于共有m個樣本的數(shù)據(jù)集,損失函數(shù)定義如下

通過梯度下降法,對神經網(wǎng)絡的超參數(shù)進行修正,使得損失函數(shù)L降低至設定值以下,從而實現(xiàn)神經網(wǎng)絡的自主學習過程.

權重W修正如下

閾值b修正如下

其中函數(shù)f與Adam 優(yōu)化器有關,在數(shù)據(jù)梯度較小的場景以較大的學習率進行更新,在數(shù)據(jù)梯度較大的場景以較小的學習率進行更新,比標準的SGD算法更有效地收斂.設置默認學習率α=0.001,ε=1 × 10?10.

根據(jù)多次訓練結果分析,當隱藏層層數(shù)等于輸入層變量個數(shù),每層神經元節(jié)點數(shù)等于輸入層變量個數(shù)3 倍時,能獲得較好的訓練效果.本文共選取7 個輸入變量,故DNN 隱藏層取7 層,每層均設置21 個神經元節(jié)點,輸出層為單一變量γpredict.

2.2 深度神經網(wǎng)絡訓練

本文DNN 訓練基于Pytorch 平臺,構建了層流流場物理量與間歇因子γ間的映射關系,目的在于實現(xiàn)數(shù)據(jù)驅動轉捩模型對三維流場橫流轉捩的精確預測.輸入層7 個變量V=R,Ωstreamwise),各變量定義如下.

用于尋找間歇因子在流向上增長位置的流向雷諾數(shù)

如圖7 所示,以NLF(2)-0415 后掠翼為例,特征距離s是翼型前緣點A到指定點B,壁面曲線的長度積分,點B處壁面法線L上所有點特征距離s與點B相同.將壁面曲線AB按照網(wǎng)格劃分進行離散,點A作為第1 個離散點,點B作為第n個離散點,特征距離s如下

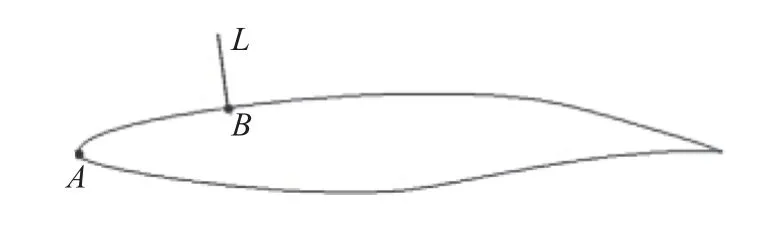
圖7 特征距離s 計算Fig.7 Calculation method of characteristic length s

用于尋找間歇因子在壁面法向上增長位置的無量綱壁面法向距離y+[34](通過程序Y+wall distance est imation 計算)

用于尋找間歇因子在壁面法向上增長位置的無量綱化的合速度

用于在流場結構層面確定間歇因子增長位置、無量綱速度對應的應變率張量、旋轉率張量的模S,R[34]

在γ-Reθ轉捩模型中用于構造無量綱橫流強度Hcrossflow、無量綱速度對應的流向渦強度Ωstreamwise[34]

本文D N N 所用的訓練數(shù)據(jù)為4 5°后掠角NLF(2)-0415 后掠翼層流狀態(tài)的計算數(shù)據(jù),以γ-Reθ轉捩模型計算得到的間歇因子γ進行監(jiān)督學習.前文已經給出45°后掠角下5 種不同雷諾數(shù)工況,并對γ-Reθ轉捩模型計算的準確性進行了校驗.對于CFD 計算結果而言,影響占比較大的是邊界層內以及邊界層附近的間歇因子γ分布情況,因此每種雷諾數(shù)下,取上翼面近壁面處i·j=101 × 81=8181 個網(wǎng)格點的數(shù)據(jù)用作訓練以及測試,如圖8 所示,即圖中白色邊線范圍內網(wǎng)格點的計算數(shù)據(jù),由速度分布可知,該區(qū)域包含了上翼面全部邊界層.

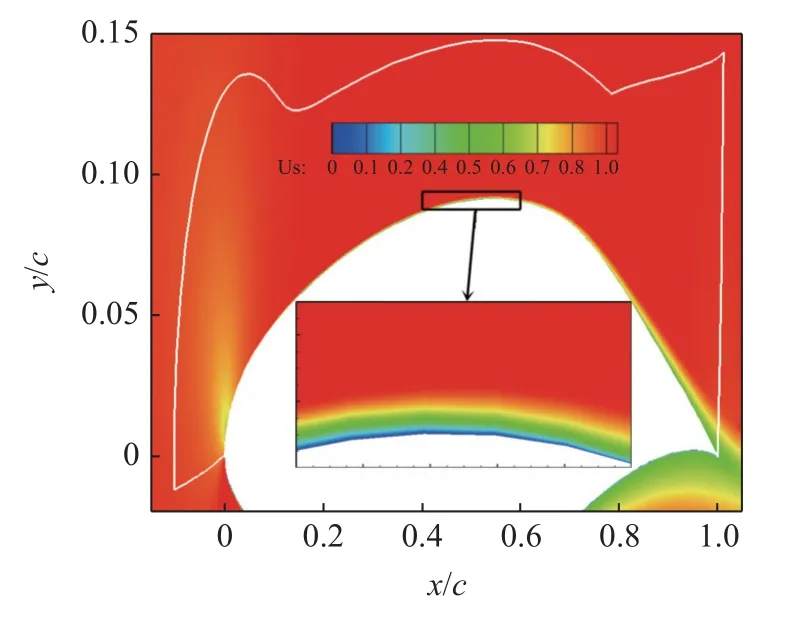
圖8 訓練數(shù)據(jù)所處區(qū)域Fig.8 The zone of data for DNN

2.3 深度神經網(wǎng)絡擬合校驗

隨著隱藏層層數(shù)以及隱藏層節(jié)點數(shù)的增加,神經網(wǎng)絡的學習能力增強,容易過度挖掘訓練樣本中特有的映射關系,并將其視為普適性規(guī)律,亦或是在已經挖掘出恰當映射關系后,進一步學習并擬合噪音樣本,從而導致訓練得到的DNN 泛化能力差,出現(xiàn)過擬合現(xiàn)象.現(xiàn)采用5 折交叉驗證的方法,以確保本研究訓練的DNN 沒有發(fā)生過擬合,5 折交叉驗證方法如圖9 所示.

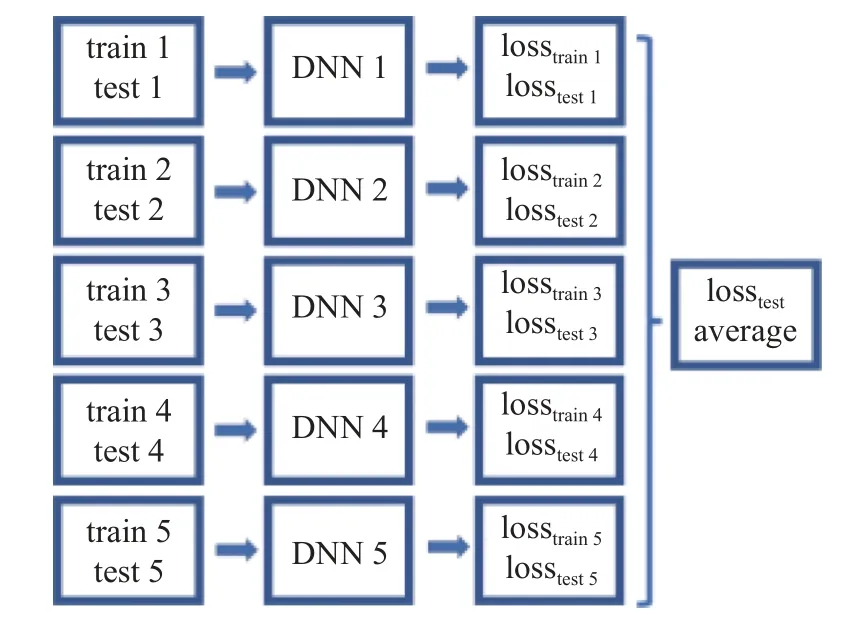
圖9 5 折交叉驗證Fig.9 5-fold cross validation

5 種工況下共提取了40905 個數(shù)據(jù)樣本,隨機均勻劃分為5 組,每組包含8181 個數(shù)據(jù)樣本.依次將每組數(shù)據(jù)樣本作為測試集,余下的4 組數(shù)據(jù)樣本作為訓練集,訓練得到DNN1～ DNN5,并計算訓練集、測試集的損失函數(shù)以及測試集損失函數(shù)的均值.5 折交叉驗證的結果見表2.

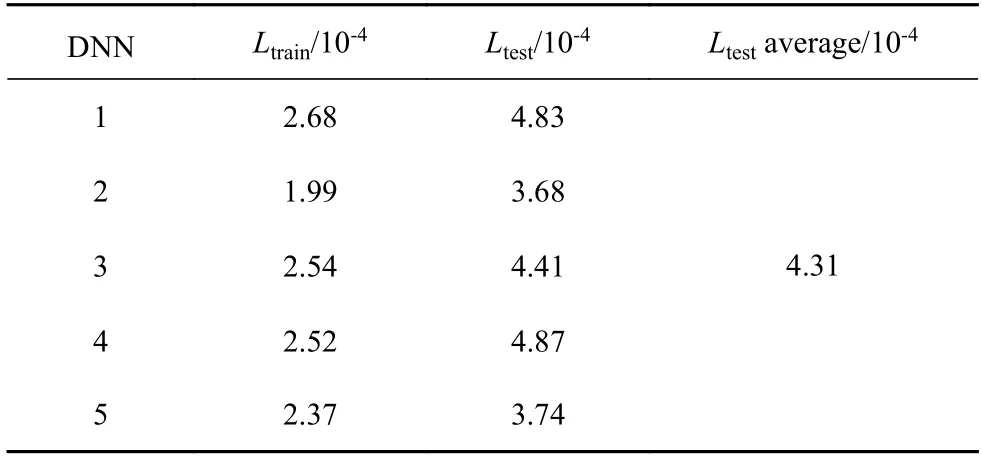
表2 交叉驗證結果Table 2 Result of cross validation

由于測試集中的數(shù)據(jù)樣本沒有參與DNN 訓練,且DNN 必然存在對特有映射關系的構建以及對訓練集噪音樣本的學習,交叉驗證中測試集損失函數(shù)高于訓練集是完全合理的.測試集損失函數(shù)、損失函數(shù)均值均維持在較低的水平,且與訓練集損失函數(shù)間的差異遠未到跨越一個或多個量級的程度,說明DNN 并沒有發(fā)生過擬合,能夠較為精準地預測間歇因子γ的分布.

3 算例分析

3.1 變雷諾數(shù)NLF(2)-0415 后掠翼測試

將NLF(2)-0415 后掠翼Re=2.37 × 106以外的其他4 種工況共32724 個數(shù)據(jù)樣本作為訓練集,對DNN 進行訓練.損失函數(shù)設置為7.50 × 10?3,完成30000步訓練后,深度神經網(wǎng)絡模型實際損失函數(shù)為2.0 ×10?4,將其作為本研究算例分析所用的數(shù)據(jù)驅動轉捩模型.以數(shù)據(jù)樣本是否參與DNN 訓練作為內插與外推的判別標準,分別用Re=2.73 × 106,Re=2.37 ×106工況下的上翼面近壁區(qū)域數(shù)據(jù)樣本對數(shù)據(jù)驅動轉捩模型進行內插與外推測試.圖10 給出了兩種工況下數(shù)據(jù)驅動轉捩模型對間歇因子預測值與γ-Reθ轉捩模型計算值的對比.

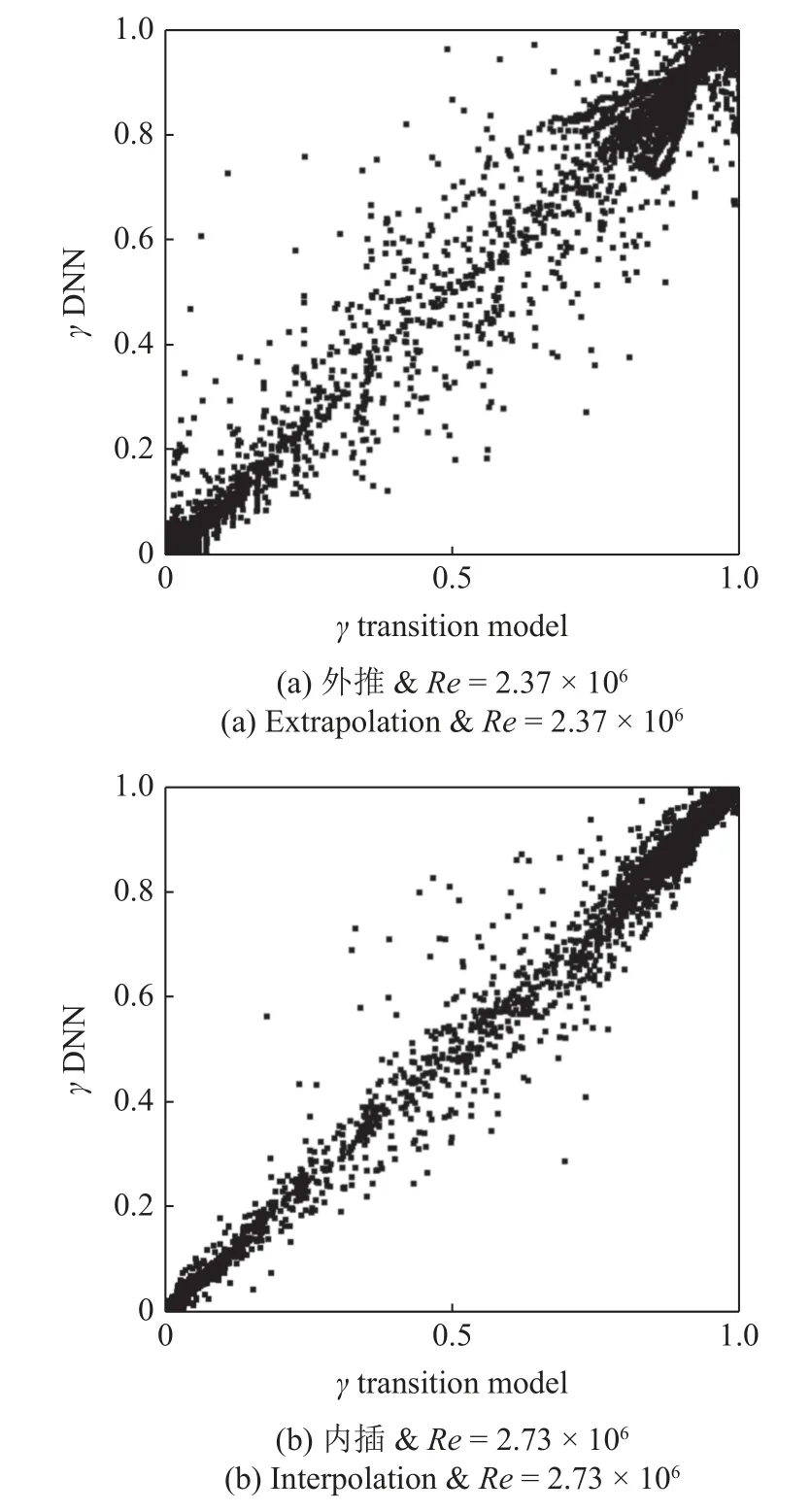
圖10 間歇因子預測值與計算值對比Fig.10 Comparison between predicted value and calculated value of intermittency

間歇因子預測值與計算值間誤差越低,散點分布越接近線性函數(shù)y=x.以此為評判標準,兩種工況下數(shù)據(jù)驅動轉捩模型對間歇因子的預測均取得了較好的效果.由于沒有參與DNN 訓練,用作外推測試的工況Re=2.37 × 106間歇因子預測結果在線性函數(shù)y=x附近離散程度較高,這與第2.3 節(jié)中測試集損失函數(shù)高于訓練集損失函數(shù)的原因一致.由圖10 可知,兩種工況下近壁區(qū)域間歇因子散點,均較為均勻地分布在線性函數(shù)y=x兩側,說明兩種工況下間歇因子預測值雖然存在不同程度的離散,但與計算值變化規(guī)律基本一致,具有良好的預測效果.

運用數(shù)據(jù)驅動轉捩模型對Re=2.73 × 106,Re=2.37 × 106工況下全流場的間歇因子γ進行預測,并與SSTk-ω湍流模型耦合,計算NLF(2)-0415 后掠翼上翼面橫流轉捩.定義Δγ為數(shù)據(jù)驅動轉捩模型間歇因子預測值減去γ-Reθ轉捩模型間歇因子計算值,用于表征數(shù)據(jù)驅動轉捩模型計算結果在空間分布上相較于γ-Reθ轉捩模型的偏差.圖11給出了上翼面近壁區(qū)域Δγ的空間分布.

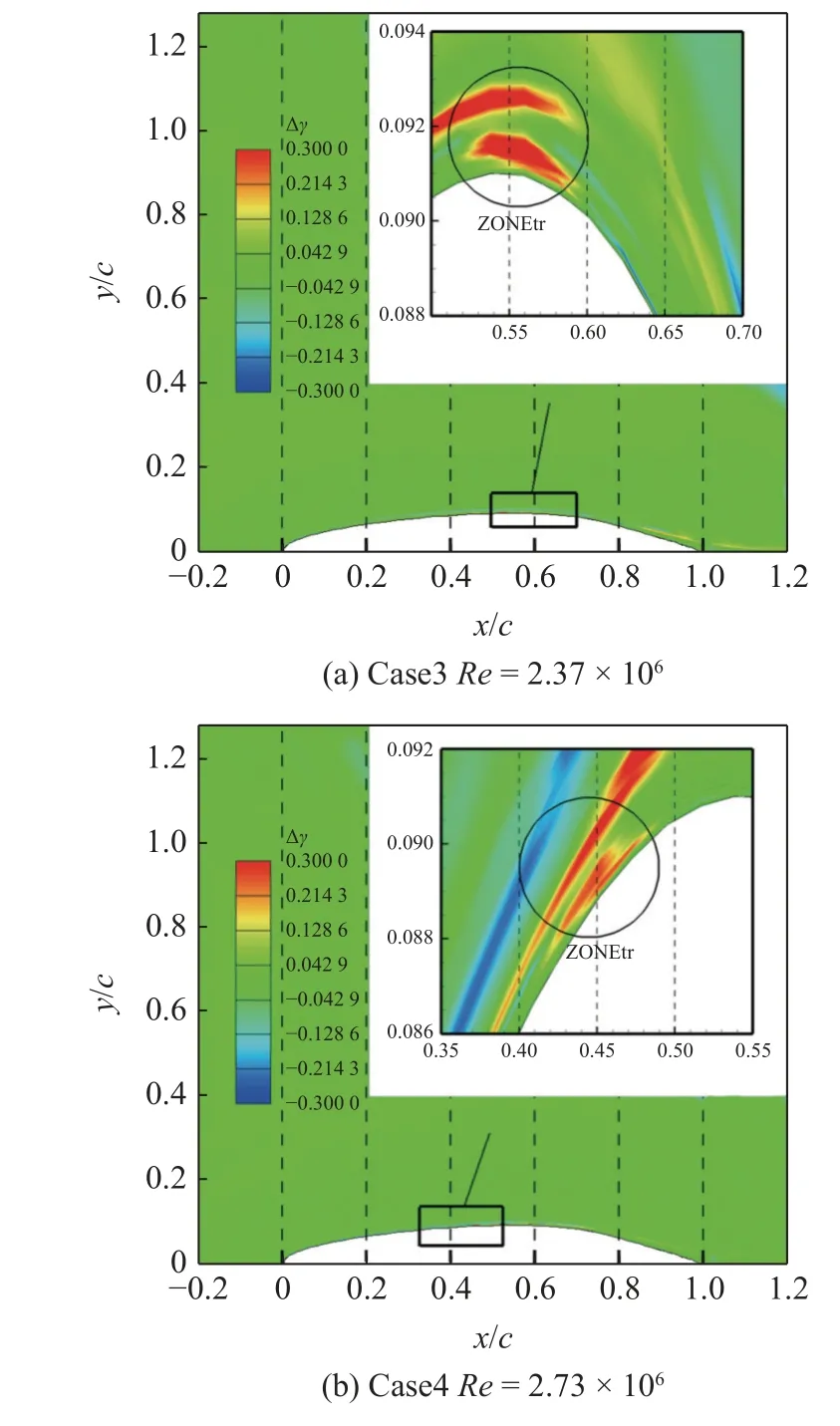
圖11 近壁區(qū)域Δγ 分布Fig.11 Distribution of Δγ near the wall

觀察圖11,在轉捩區(qū)域(即圖11 中ZONEtr)貼近壁面處,少部分網(wǎng)格點Δγ大于0,說明數(shù)據(jù)驅動轉捩模型存在將近壁區(qū)域間歇因子低值點預測出高值的問題.其中工況Re=2.37 × 106的數(shù)據(jù)未參與DNN 訓練,數(shù)據(jù)驅動轉捩模型預測出現(xiàn)誤差的網(wǎng)格點數(shù)量多于工況Re=2.73 × 106.

以上翼面的Cf曲線作為數(shù)據(jù)驅動轉捩模型預測精度的判斷標準,兩種工況下耦合測試的結果如圖12 所示.

由圖12 可以看出,兩種工況下數(shù)據(jù)驅動轉捩模型計算得到的Cf上翼面分布曲線與γ-Reθ轉捩模型計算結果吻合較好,其中數(shù)據(jù)驅動轉捩模型計算的轉捩位置略微提前.

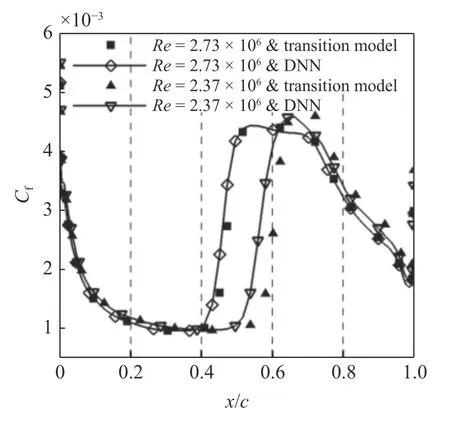
圖12 數(shù)據(jù)驅動轉捩模型與γ-Reθ 轉捩模型Cf 計算結果Fig.12 Cf of data driven transition model and γ-Reθ transition model

對數(shù)據(jù)驅動轉捩模型預測轉捩位置出現(xiàn)提前的問題進行分析.由圖12 可知,工況Re=2.37 ×106下,外插測試的轉捩位置提前幅度偏大.前文已經對間歇因子預測值的誤差進行了分析,將近壁區(qū)域內少量間歇因子低值點預測出較高的值,會導致渦黏性系數(shù)μt的高值區(qū)域范圍增大,使得μt在網(wǎng)格流向與壁面法向上的增長提前,從而導致預測的轉捩位置更為靠前.

以工況Re=2.37 × 106下的NLF(2)-0415 后掠翼轉捩預測過程為例,采用CPU 時間作為參照標準,使用本研究的預測方法,層流流場計算2 萬步至收斂需要3467 s,數(shù)據(jù)驅動轉捩模型輸出間歇因子的時間忽略不計(不足10 s),耦合SST 模型計算5 萬步至收斂需要14796 s,共需要計算7 萬步,耗時約18000 s;使用γ-Reθ轉捩模型與SST 模型耦合計算5 萬步至收斂,耗時22660 s.對比可知,本研究提出的轉捩預測方法可以節(jié)約近20%的CPU 時間,一定程度提高了計算效率.

3.2 變后掠角NLF(2)-0415 后掠翼預測

NLF(2)-0415 后掠翼在后掠角足夠小時,邊界轉捩主要為流向轉捩,轉捩位置靠近機翼后緣;隨著后掠角的增大,邊界層橫流轉捩位置逐漸前移,并在后掠角為55°左右時橫流轉捩位置最靠近機翼前緣,隨后逐漸后移[43].延用圖2 的計算網(wǎng)格,保持其他工況不變,運用數(shù)據(jù)驅動轉捩模型預測后掠角為45°～65°,Re=2.73 × 106工況下NLF(2)-0415 后掠翼上翼面的橫流轉捩過程,上翼面流線如圖13 所示.

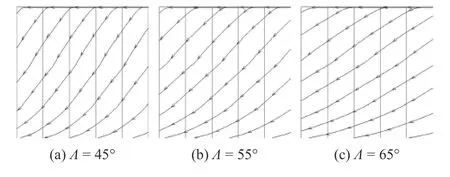
圖13 上翼面流線Fig.13 Streamline of upper wing

表3 給出了數(shù)據(jù)驅動轉捩模型與Zlow 平臺γ-Reθt-CF-模型對轉捩位置的計算結果[43]的對比.

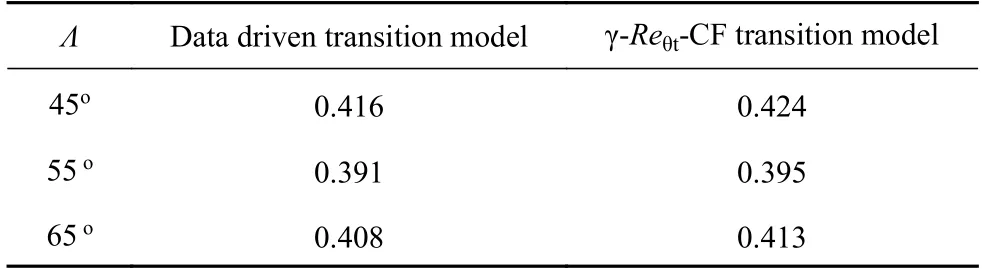
表3 數(shù)據(jù)驅動轉捩模型與γ-Reθt-CF 轉捩模型對轉捩位置的計算結果對比Table 3 Comparison of xtr between data driven transition model and γ-Reθt-CF transition model

由表3 可知,數(shù)據(jù)驅動轉捩模型在不同后掠角工況下計算得到的轉捩位置與γ-Reθt-CF 轉捩模型基本一致,證明本研究的數(shù)據(jù)驅動轉捩模型對改變來流條件的橫流轉捩預測具有一定的泛化能力.

后掠角從45°向65°增大,數(shù)據(jù)驅動轉捩模型計算的轉捩位置出現(xiàn)了先向機翼前緣移動,再向機翼后緣移動的現(xiàn)象,其中后掠角55°時轉捩位置最為靠前,與文獻[43]給出的轉捩位置變化規(guī)律完全一致.相較于后掠角45°,后掠角65°下轉捩位置略微靠前,盡管區(qū)別很小,但數(shù)據(jù)驅動轉捩模型依然準確識別了這個細微的差異.

以上分析表明,僅用NLF(2)-0415 后掠翼45°后掠角計算數(shù)據(jù)訓練得到的數(shù)據(jù)驅動轉捩模型能夠用于不同后掠角下的橫流轉捩預測,具備一定的泛化能力,下一步將針對不同外形的橫流轉捩進行模型測試.

3.3 6 : 1 標準橢球體預測

6 : 1 標準橢球體是典型低速三維轉捩標模.在迎角為15°,單位雷諾數(shù)為6.5 × 106/m,馬赫數(shù)為0.136 的工況下,橢球體表面邊界層轉捩由橫流轉捩主導[42],具體計算工況見表4.現(xiàn)將數(shù)據(jù)驅動轉捩模型用于預測6 : 1 標準橢球體表面的轉捩過程,以進一步校驗其泛化能力.

表4 橢球體計算工況Table 4 Conditions of ellipsoid

本文共對橢球體劃分3 套計算網(wǎng)格,如圖14所示,網(wǎng)格量分別為43 萬、180 萬和330 萬,在保證網(wǎng)格法向j上第1 層網(wǎng)格y+≈3 的前提下,通過改變流向i、法向j、周向k的網(wǎng)格數(shù)量、增長率來改變網(wǎng)格總量,分別命名為Mesh A,Mesh B,Mesh C.

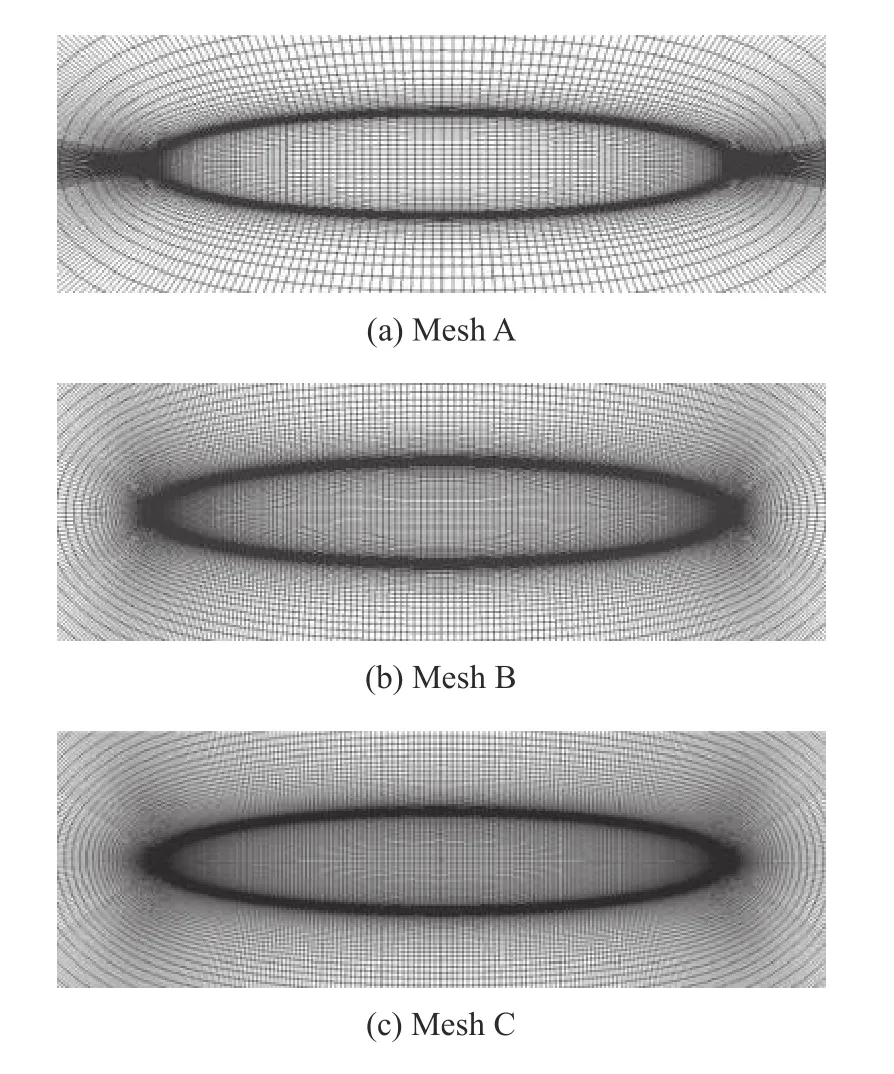
圖14 橢球體計算網(wǎng)格Fig.14 Computing mesh for ellipsoid

圖15 給出了本文3 套網(wǎng)格下,橢球體上下表面交界線上,層流流場、湍流流場和轉捩流場的Cf分布.

由圖15 可知,對于層流狀態(tài)和湍流狀態(tài),3 套網(wǎng)格計算得到的Cf分布并無明顯差異,但求解γ-Reθ轉捩模型后,高分辨率Mesh B,Mesh C 計算得到的Cf分布基本重合,與低分辨率Mesh A 存在較大差異.以上分析表明,對于層流與湍流流場的計算,低分辨率的Mesh A 已經滿足網(wǎng)格無關性,但運用γ-Reθ轉捩模型求解轉捩流場,要求網(wǎng)格分辨率達到Mesh B 以上.由于數(shù)據(jù)驅動轉捩模型輸入數(shù)據(jù)為層流流場物理量,輸出量γ直接與湍流模型耦合,因此層流流場與湍流流場計算結果準確與否,對數(shù)據(jù)驅動轉捩模型預測結果影響較大.

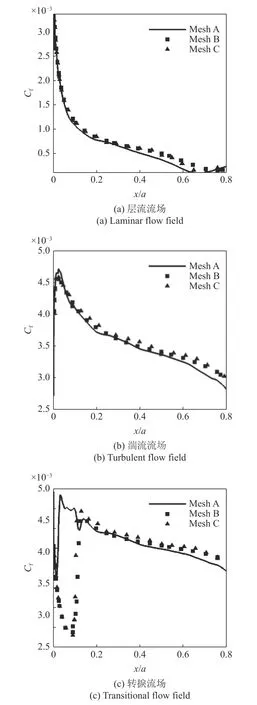
圖15 不同流動狀態(tài)的Cf 分布Fig.15 Cf distribution in different flow states

現(xiàn)采用低分辨率Mesh A 計算層流流場,并提取層流流場物理量輸入數(shù)據(jù)驅動轉捩模型,用于預測間歇因子γ.圖16 給出了y+≈30 處數(shù)據(jù)驅動轉捩模型預測的間歇因子分布,并與中等分辨率Mesh B 計算的轉捩流場間歇因子分布進行對比.

觀察圖16,數(shù)據(jù)驅動轉捩模型對橢球體迎風面橫流轉捩的起始位置預測略微提前,但仍具有較高預測精度.在2 次預測出橫流轉捩后,均發(fā)生了不同程度的再層流化.造成這個問題的可能原因如下.

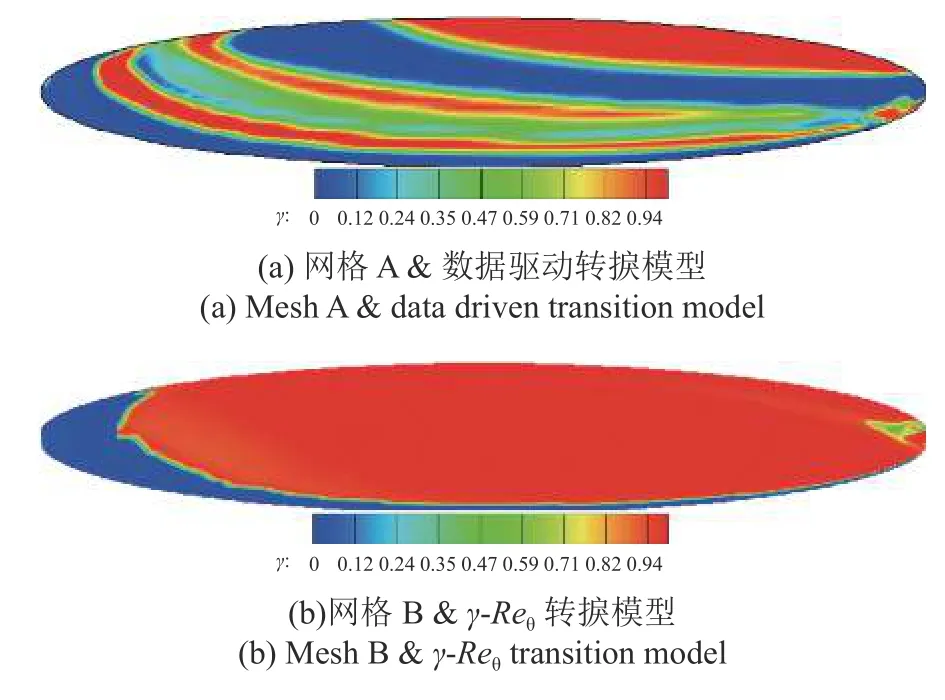
圖16 y+≈30 處間歇因子分布Fig.16 Distribution of γ in y+≈30

DNN 僅依靠單一網(wǎng)格點的輸入物理量對該點間歇因子進行孤立預測,在預測出大范圍轉捩后,無法進一步考慮擾動在流向上的傳遞、疊加,進而修正轉捩區(qū)域后側流場間歇因子的預測值.

基于上述推論,本研究對數(shù)據(jù)驅動轉捩模型補充了考慮擾動傳遞、疊加的算法限制,使其輸出的間歇因子預測值在自由來流方向上不會錯誤地產生衰減,如圖17 所示.

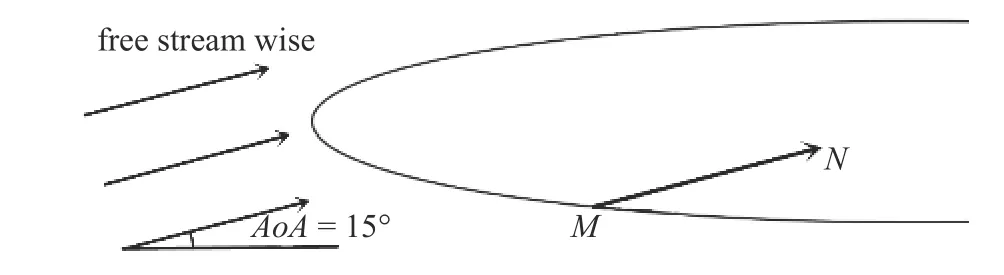
圖17 算法限制原理Fig.17 The theory of algorithm

首先利用數(shù)據(jù)驅動轉捩模型對流場中所有網(wǎng)格點的間歇因子γ進行預測.在自由來流方向,即圖17中MN指向上,若某網(wǎng)格點的間歇因子γ預測值低于前側距離最近的網(wǎng)格點,則使用前側網(wǎng)格點的γ預測值對其重新賦值,從而保證自由來流方向上間歇因子γ預測值始終遞增.考慮到橢球體最前端存在少量γ接近1 的高值點,直接啟用此算法會導致大量網(wǎng)格點間歇因子被錯誤地賦為高值,因此算法僅對x/a＞0.05 (橢球體長軸a=2.4 m,即x＞0.12 m)的網(wǎng)格點預測值進行限制.圖18 給出了補充算法限制后y+≈30 處間歇因子預測值.

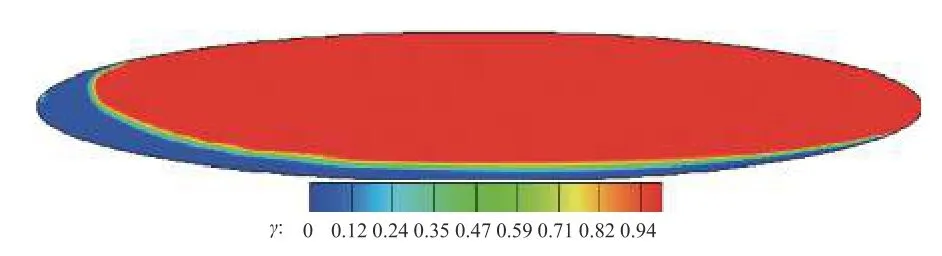
圖18 補充算法限制后間歇因子分布Fig.18 Distribution of γcorrect

補充算法限制后的間歇因子分布與圖16(b)基本一致,具有較高的預測精度.繼續(xù)采用低分辨率Mesh A,將數(shù)據(jù)驅動轉捩模型預測的間歇因子γ以及補充算法限制后的間歇因子γcorrect分別與SSTk-ω湍流模型耦合,計算橢球體表面轉捩過程,并與本研究使用的γ-Reθ轉捩模型、Chant 平臺橫流模型[35]、BCDF-CF 代碼[34]、OVERFLOW-CF 代碼[34]計算結果、實驗結果[44]對比,如圖19 所示.

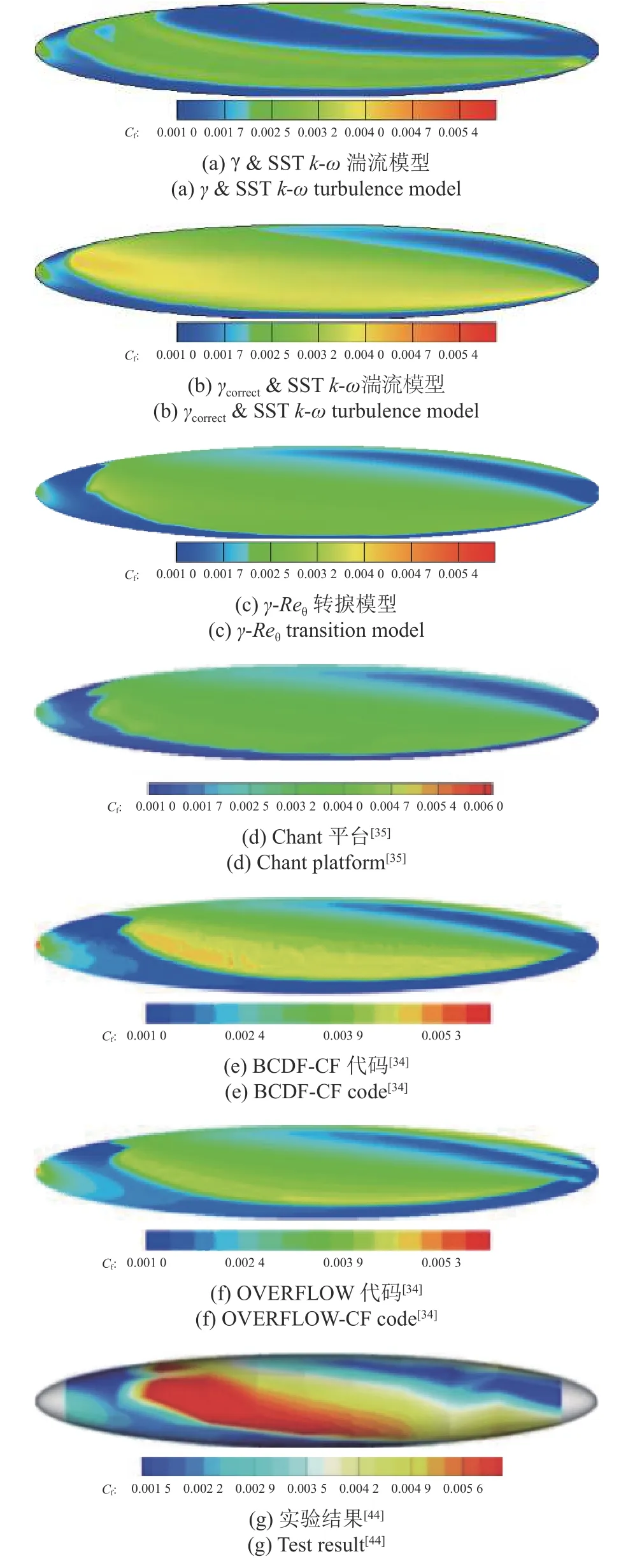
圖19 不同算法對Cf 的預測結果以及實驗結果Fig.19 Cf of different methods and test

觀察圖19(a),對數(shù)據(jù)驅動轉捩模型補充限制修正前,橢球體表面Cf分布依然能夠反映出轉捩陣面的形狀,但轉捩與湍流區(qū)域Cf峰值較低,且第2 次預測出橫流轉捩后發(fā)生的再層流化較為明顯.觀察圖19(b),對數(shù)據(jù)驅動轉捩模型補充算法限制后,對轉捩陣面形狀的預測能力與本研究使用的γ-Reθ轉捩模型、Chant 平臺橫流轉捩模型[35]、Langtry 等[34]給出的兩套代碼相仿,但在轉捩位置預測上依然存在一定程度的提前;層流區(qū)域Cf谷值約為0.001,轉捩與湍流區(qū)域Cf峰值大于0.003,與本研究使用的γ-Reθ轉捩模型、Chant 平臺橫流轉捩模型[35]、Langtry等[34]使用的兩套代碼計算結果基本一致,Cf值均略低于實驗結果[44].

以上結果表明,數(shù)據(jù)驅動轉捩模型在顯著降低計算成本的同時,具有良好的橫流轉捩預測能力,實現(xiàn)了對橢球體表面橫流轉捩的預測.

4 結論

本文運用數(shù)據(jù)驅動對三維橫流轉捩進行了預測,結論如下.

(1) 選取層流流場轉捩相關物理量對DNN 進行訓練,獲得的數(shù)據(jù)驅動轉捩模型能夠預測變雷諾數(shù)的NLF(2)-0415 后掠翼上翼面橫流轉捩過程,預測轉捩位置有小幅度提前,具有較高預測精度.

(2) 由變雷諾數(shù)的NLF(2)-0415 后掠翼計算數(shù)據(jù)訓練得到的數(shù)據(jù)驅動轉捩模型具有較好的泛化能力,可以預測變后掠角NLF(2)-0415 后掠翼上翼面的轉捩位置,以及橢球體的三維邊界層橫流轉捩.

(3) 數(shù)據(jù)驅動轉捩模型與湍流模型耦合的轉捩預測方法,需保證層流、湍流流場的計算精度,在減少整個計算過程所需求解輸運方程數(shù)量的同時,進一步降低了對網(wǎng)格分辨率的要求,實現(xiàn)高效轉捩預測.使用同一套計算網(wǎng)格,相比于γ-Reθ轉捩模型,數(shù)據(jù)驅動轉捩模型能夠節(jié)省近20%的計算時間.

各種因素與邊界層轉捩間具有復雜的影響機理,如提高粗糙度會導致橫流轉捩起始位置前移,如流動分離也會引發(fā)邊界層轉捩.針對某個表面粗糙度設計,僅具備較強橫流轉捩模態(tài)識別能力的數(shù)據(jù)驅動轉捩模型,難以完全滿足工程應用或科研工作的需求.在下一步工作中,將針對變粗糙度、多轉捩模態(tài)下間歇因子的預測展開研究工作,嘗試在保證數(shù)據(jù)驅動轉捩模型橫流轉捩預測精度的前提下,實現(xiàn)對包括橫流轉捩在內的多轉捩模態(tài)識別,并適用于不同加工精度的表面,提高數(shù)據(jù)驅動轉捩模型的應用范圍.