基于收斂-約束法的軟巖隧道初支時機估算
——以義永公路楓坑隧道為例

梁譯文， 查文華*， 吳波， 劉造保， 楊明， 劉小虎

(1.東華理工大學土木與建筑工程學院， 南昌 330013； 2.東北大學資源與土木工程學院， 沈陽 110819； 3.中煤第三建設(集團)有限責任公司市政工程分公司， 合肥 230031； 4.安徽理工大學土木建筑學院， 淮南 232001)

地下空間支護結構設計的發展，經歷了力學模型從粗略到精細、結構從單一到多樣、從經驗設計逐步上升到理論分析的過程[1]；現代支護理論則[2-3]是將圍巖與支護結構作為一個整體，最大限度發揮圍巖自承載能力；而支護結構的本質作用在于：調動、協助圍巖的承載作用。

支護結構調動、協助的前提是合理施作支護時機及支護剛度；收斂-約束法[4-5]所闡述的圍巖縱向變形曲線能直觀地、有效地反映了隧道開挖過程中洞壁圍巖變形受掌子面前端空間效應的影響，并為支護結構最佳時機施作提供理論依據。

當前許多學者基于收斂-約束法原理探討了隧道開挖過程中圍巖變形、支護壓力、支護時機等相關問題：張光偉等[6]通過采用現場監測和數值模擬相結合的方法，提出高地應力作用下軟巖隧道初支合理施作時機。梁鵬等[7]通過引入巖體破壞接近度指標FAI(failure approach index)和考慮巖體應變軟化特性，建立了隧道最優支護時機方法。唐雄俊[8]通過引入初支屈服軸力與圍巖變形折減率作為合理支護時機的判據，分析不同圍巖質量、支護類型、初始應力、臨界塑性軟化系數、剪脹角下，給出深埋隧道合理支護時機；王永剛等[9]通過對比現場監測數據，從應力釋放、降低二襯擠壓形變壓力的角度，開展了炭質板巖隧道二襯施作時機研究；唐霞等[10]通過分析監測數據和建立圍巖蠕變特性模型，推導了二次襯砌合理時機；周建等[11]通過考慮空間效應、襯砌時效以及支護結構施加時機，構建隧洞力學模型，推導出洞壁位移以及支護壓力解析解；蘇凱等[12-13]通過構建荷載釋放率和掌子面與監測斷面間的關系式，研究了最佳初支時機和開挖面空間效應等問題。張妍珺等[5]基于收斂-約束法在分析隧道開挖過程中圍巖變形規律，發現圍巖位移的收斂規律與圍巖質量相關，提出隧洞縱向變形曲線的修正公式，并對合理設置初支時機進行估算。但針對考慮掌子面前端空間效應作用下，圍巖縱向變形曲線和不同圍巖支護時機等問題，學者們并沒有給出很好的解釋。

基于此，現以永康市義永公路楓坑軟巖大斷面隧道為例：①通過對比分析現場監測數據和理論計算數據，在綜合考慮泊松比和彈性模量以及黏聚力、內摩擦角、爆破參數等，針對Unlu和Gercek推導的圍巖縱向變形曲線方程提出改進；②通過試驗和數值擬合給出擴大收斂函數的相關參數；③運用FLAC3D分析改進的圍巖縱向變形曲線方程的合理性和有效性；④提出位移增量出現陡增點時的圍巖位移釋放系數值為施加支護的最佳時機，得出不同圍巖施加支護與掌子面之間的控制距離。

1 收斂-約束法與空間效應及位移釋放系數特性分析

1.1 收斂-約束法基本原理

隧道的開挖是一個時間與空間上動態變化的復雜過程，有效地掌握圍巖前期變形和開挖后巖體與支護結構的相互作用關系以及有效地估算巖體與支護體系的各項應力與位移，依據現場監控量測資料，設計出最佳支護時機和支護體系，是收斂-約束法理論分析的主要目的。

收斂-約束法基本原理[14-15]如圖1所示，其包括圍巖特征曲線(ground reaction curve，GRC)、圍巖縱向變形曲線(longitudinal deformation profile，LDP)、支護結構特征曲線(support characteristic curve，SCC)。

(1)圍巖特性曲線(GRC)：闡述了隧道圍巖徑向位移與徑向壓力之間的關系，當徑向位移為0時，圍巖壓力等于初始地應力P0；當圍巖壓力為0時，隧道徑向最大umax，此時為無任何支護的情況。圍巖特性曲線大體上可分為3個階段，直線段為彈性變形階段，曲線段為塑性變形階段，虛線段為失穩破壞階段。

(2)縱斷面變形曲線(LDP)：刻畫了位于掌子面前后方一定距離內x(一般為3～5倍洞徑)，未開挖的圍巖對已開挖的圍巖存在空間約束作用，u0為監測斷面圍巖前期變形量。

(3)支護特征曲線(SCC)也稱約束變形曲線，是指不同剛度的支護結構作用過程，交點D的縱坐標pD為作用在支護結構上的最終圍巖壓力，交點D的橫坐標uD為圍巖的最終變形量。

1.2 空間約束效應

隧道開挖是空間與時間組成的四維變化問題[16]，特別是在掌子面附近，前方未開挖的巖體對后方一定距離的圍巖有半穹頂的空間約束效應，而且圍巖壓力的釋放不是瞬間完成的，而是隨著掌子面的逐漸遠離而逐漸釋放的。

隧道開挖支護施作的模擬過程[17]如圖2所示，其中，隧道掘進方向自左向右，開挖一個進尺后開始施作支護，而后支護與開挖協同并進，斷面A-A′為監測斷面；xa為掌子面對前后圍巖方影響距離，一般取3倍洞徑。t=t0時刻，受空間效應的影響A-A′斷面處圍巖開始產生變形，圍巖應力開始釋放；t=t1時刻，監測斷面A-A′恰好位于掌子面處且無支護，圍巖壓力迅速釋放，圍巖產生一定的隱性位移u0(無法監測位移)，但由于前方圍巖的約束作用，圍巖位移沒有達到最大值umax，圍巖應力小于原巖應力p0；t=t2時刻，掌子面對監測斷面A-A′不在有空間約束效應，此階段支護結構不足或不當將導致圍巖過大變形出現坍塌、冒頂等事故，同時也是圍巖與支護結構相互作用達到平衡的階段。

1.3 位移釋放系數分析

對于復雜的彈塑性問題，其應力與應變之間的關系不再滿足簡單的胡克公式，而是取決于其材料的塑性本構關系[18]；為了更加清晰直觀地研究隧道掌子面的空間效應，定義位移釋放系數λ(x)來描述掌子面的空間效應；位移釋放系數λ(x)是掌子面一定距離x處某點的圍巖徑向位移u(x)與掌子面距離足夠遠(不受掌子面空間約束效應影響)的同一位置、同一方向上的徑向位移u(∞)之比。

(1)

圍巖徑向位移u(∞)，可由經驗公式求出，即

(2)

式(2)中：M=2P0sinφ+2ccosφ，為彈塑性邊界應力差；P0為原始應力；R為隧道開挖半徑；R0為隧道開挖塑性區半徑；G為巖體剪切模量；φ為巖體內摩擦角；c為巖體黏聚力。

能否有效地將位移釋放系數λ(x)運用到計算圍巖縱向變形曲線，是當前學者一直探討的重點；目前針對移釋放系數λ(x)在表示圍巖縱向變形曲線的計算公式如下。

Panet等[19]利用三維有限元彈性分析，獲得了x≥0時的位移釋放系數關系式，即

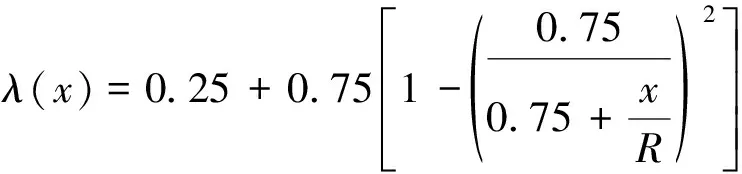
(3)

Corbetta等[20]采用彈性應力分析方法，提出了x≥0時的位移釋放系數關系式為

(4)

式(3)和式(4)在掌子面處的位移釋放系數分別0.25和0.29；其只適合x≥0段，與實際工程相悖。

實際地下工程施工中圍巖常常會出現塑性變形，研究圍巖塑性變形階段的位移釋放系數顯得更加重要。關于圍巖在彈塑性變形情況下，圍巖位移釋放系數的關系式如下。

Vlachopoulos等[21]基于彈塑性模型和H-B強度準則，運用FLAC3D進行模擬演算，構建以塑性半徑R為基礎的V-D(09)位移釋放系數，即

(5)

式(5)中：相對半徑R*=R/r；相對位置x*=x/r；λ0為距掌子面x=0處的位移釋放系數。

Hoek等[22]采用最佳擬合的方法，建立了洞壁徑向位移與掌子面距離之間的經驗關系公式為

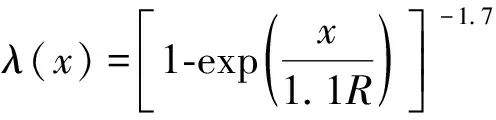
(6)

式(6)在掌子面的位移釋放率為0.31。

雖然式(5)和式(6)在描述圍巖縱向變形曲線取得了一定成果，但多是經驗推測和數值擬合獲得，沒有考慮隧道開挖過程圍巖參數的變化所帶來的影響，具有一定的局限性。

Unlu等[23]考慮泊松比的影響，提出較為符合工程實際的位移釋放系數關系式，其分段性更便于實際工程的應用；但該關系式僅考慮泊松比對位移釋放系數的影響，未對巖體其他參數給予解釋，其他參數的影響有待進一步研究。

(7)

式(7)中：υ巖體的泊松比；x為到掌子面的距離；R為隧洞開挖半徑。

2 圍巖縱向變形曲線求解分析

2.1 工程概況

楓坑隧道位于浙江省金華市永康市境內為一分雙體洞隧道，進出洞口位于丘陵斜坡和溝谷附近，植被發育自然坡度20°～45°，設計斷面半徑為7 m。圍巖多為強風化-中風化巖體，青灰色、綠灰色，巖體呈碎塊狀鑲嵌結構，裂隙發育，較破碎；依據勘測報告和隧道設計施工圖可知：隧道右線斷面ZK30+480、ZK30+590、ZK30+905所在位置圍巖[BQ]=310～450，綜合評定為Ⅲ級，埋深約100～160 m，其上覆地層的平均密度約為2 300 kg/m3；斷面ZK31+485、ZK31+560、ZK31+650所在位置圍巖[BQ]=254～310，綜合評定為Ⅳ級，埋深約60～120 m，其上覆地層的平均密度約為2 000 kg/m3。其中隧道規劃及現場情況如圖3所示。

實際施工過程中，針對Ⅲ級圍巖采用長臺階法開挖支護，Ⅳ級圍巖采用CRD工法進行開挖支護，隧道開挖步距約為3.5 m，拱頂監測點布設在距掌子面0.2 m處；隧道開挖支護示意圖如圖4所示，圍巖與支護結構參數，如表1所示。

圖3 隧道開挖示意圖Fig.3 Schematic diagram of tunnel excavation

圖4 隧道開挖示意圖Fig.4 Schematic diagram of tunnel excavation

表1 圍巖與支護物理力學參數Table 1 Physical and mechanical parameters of

2.2 現場數據監測分析

新奧法施工原則是少擾動、早噴錨、勤量測、緊封閉，即在充分利用圍巖自身的承載能力，通過錨噴鋼拱架等柔性支護，使圍巖-支護結構體系共同承擔應力釋放產生的荷載，并通過監控量測的數據分析、預測和反饋，來實現隧道施工的信息化。

圍巖與支護結構的許多特性，都可以通過變形來宏觀反映，即通過監控量測獲取圍巖的收斂位移是評價圍巖承載能力最直觀、最有效的信息元素。隧道監測項目分為：必測項目和選測項目；根據現場實際情況，現場采用高精度全站儀結合棱鏡或反光片進行測量。如圖5所示。

對Ⅲ級圍巖斷面ZK30+480、ZK30+590、ZK30+905以及Ⅳ級斷面ZK31+485、ZK31+560、ZK31+650的拱頂、凈空等變形數據研究，繪制其變形與持續時間的圍巖變形曲線。如圖6所示。

圖5 現場監測量測圖Fig.5 Field monitoring and measurement map

通過分析圍巖變形曲線可知：①各斷面在掌子面開挖后無論是拱頂還是凈空位移初期呈近似線性變化，下導開挖時位移出現彎折突增的現象；②現場實測各斷面監測位移變形量為Ⅲ級圍巖斷面ZK30+480、ZK30+590、ZK30+905拱頂累計沉降分別為10.86、12.32、13.28 mm；凈空累計收斂分別為9.88、10.14、12.02 mm。Ⅳ級斷面ZK31+485、ZK31+560、ZK31+650拱頂累計沉降分別為11.92、12.2、14.16 mm凈空累計收斂分別為9.28、10.16、11.2 mm。

由于開挖擾動和掌子面“空間效應”，支護結構施作前或監測點埋設前，圍巖已經發生了前期變形。其變形位移計為u0，根據Unlu等[23]提供給的位移釋放系數公式[式(7)]。

取x=0.2 m，可求得各斷面圍巖位移總的變形量，如表2所示。

圖6 監測斷面拱頂和凈空圍巖變形曲線Fig.6 Deformation curve of arch crown and clearance surrounding rock of monitoring section

表2 圍巖擬合參數圍巖整體變形量Table 2 Overall deformation of surrounding rock

2.3 數據對比及公式優化分析

2.3.1 實際與理論對比分析

依據現場監測資料，將Ⅲ級圍巖斷面ZK30+480、ZK30+590、ZK30+905和Ⅳ級圍巖斷面ZK31+485、ZK31+560、ZK31+650的監測數據與理論公式[式(7)]計算數據進行對比分析，如圖7所示。

對圖7中的曲線進行擬合，得到各擬合曲線的方差和相關系數如表3所示。

結果顯示：其整體效果較好，但存在一定誤差，特別在距監測面的距離比0～2，式(7)的位移陡增速率相對緩慢，與工程實際施工監測數據存在一個滯后的時差(監測數據顯示該段位移釋放系數出現陡增，辨明了掌子面空間效應存在性)，并且與陡增后存在逐步增加段的規律也不符。以此為出發點，為提高擬合精度，在式(7)的基礎上特對x≥0段函數進行優化改進。

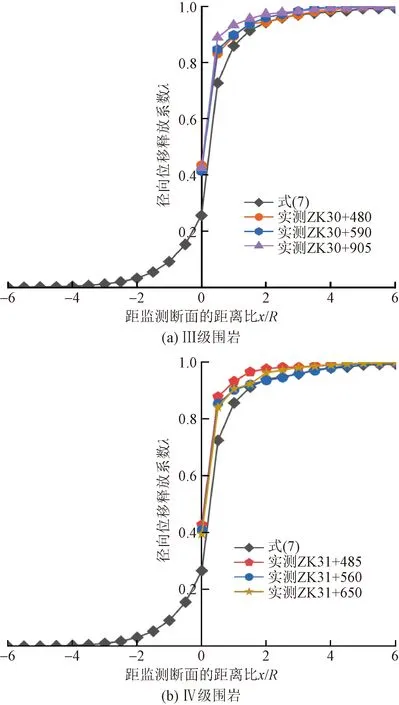
圖7 拱頂位移釋放系數監測與理論擬合圖Fig.7 Monitoring and theoretical fitting diagram of vault displacement release coefficient

2.3.2 公式優化改進

監測數據與理論計算對比顯示，隧道實際施工時圍巖變形較理論推導要提前：表明圍巖位移釋放系數除與泊松比有關，還與彈塑性模量E和內摩擦角φ、黏聚力c以及爆破參數等有關。

(1)抗剪強度與莫爾圓相互關系如圖8所示：刻畫了相同內摩擦角φ下，黏聚力c越大，圍巖強度包線范圍越廣，則圍巖承載能力較好；同理相同黏聚力c下，內摩擦角φ越大，圍巖強度包線范圍越廣，則圍巖承載能力較好；推測位移釋放系數與內摩擦角φ和黏聚力c呈非線性正比關系。

(2)由巖體抗壓強度試驗可知：圍巖的承載性與體積模量K和剪切模量G有關；在泊松比一定的情況下，體積模量K和剪切模量G與彈性模量E呈正比關系[K=E/(1-2υ)，G=E/2(1+υ)]；推測位移釋放系數與彈性模量E呈非線性正比關系。

(3)爆破使得巖體的完整性遭到巨大破壞，大大降低了巖體的彈性模量E和黏聚力c；推測位移釋放系數與爆破參數呈非線性反比關系。

掌子面附近存在如下規律：由于施工爆破和應力釋放使巖體受損，導致巖體內部產生裂隙圍巖承載能力降低，這是監測數據與理論計算存在偏差的主要原因；所以針對理論公式(7)在x≥0段提出增加擴大收斂函數，提高理論公式的實用性；已知的基本函數中指數函數(y=e-x)在x≥0是一個最大值為(y0=1)的收斂減函數，其變形規律滿足擴大收斂函數的要求；得到擴大收斂函數，即

k(x)=m+exp(-nx/R)

(8)

式(8)中：m、n為與彈性模量E、內摩擦角φ、黏聚力c和爆破參數有關的擬合參數。

圖8 巖體M-C屈服強度準則Fig.8 M-C yield strength criterion of surrounding rock

表3 圍巖擬合參數Table 3 Fitting parameters of surrounding rock

將擴大收斂函數、抗剪強度與莫爾圓其相關關系繪制在同一個坐標軸上，其相互關系如圖9所示。

通過聯立求解擴大收斂函數、抗剪強度與莫爾圓式[式(9)]交點A(a1、b1)、B(a2、b2)關系，可獲得帶有參數的擬合參數表達關系式[式(10)]。

(9)

(10)

式中：x為到掌子面的距離；R為隧洞開挖半徑；τ為巖體抗剪強度；σ1、σ3為巖體的最大最小主應力，其值可通過試驗獲取；彈性模量E、內摩擦角φ、黏聚力c和爆破參數等可通過地質勘測獲得；a1、a2為擬合參數。

通過上述分析，將提出的擴大收斂函數公式(8)與Unlu等[23]給出理論公式(7)，相結合得到修正公式(11)(根據提出優化改進的特點，改進的公式主要適合于軟巖或圍巖較破碎巖體，特別是隧道開挖后圍巖變形破壞較嚴重，相關參數變化較大的巖體)。

圖9 擴大收斂函數、抗剪強度與莫爾圓相互關系圖Fig.9 Relationship between expanded convergence function， shear strength and Mohr circle

(11)

為進一步驗證擴大收斂函數的合理性，開展了巖體的單軸壓縮試驗；試驗在DSCC-5000多通道電液伺服閉環控制系統上進行，選取3個試樣標號為N-1～N-3，N代表凝灰巖。試驗加載方式通過荷載控制，加載速率控制在0.5 MPa/s。如圖10所示將制備好的巖樣放置在平臺上，以0.5 MPa/s沿軸向施加荷載，直至試樣破壞。

圖11為圍巖應力應變關系曲線，分析除N-2以外，其余兩個中風化凝灰巖試樣單軸抗壓強度均在20 MPa以下，表現出軟巖的力學性質。通過計算獲得中風化凝灰巖平均彈性模量約3.0 GPa，屈服應力約6.0 MPa，峰值應力約為15.85 MPa。其他相關參數如表1所示；經擬合對比分析得到擴大收斂函數相關參數取m=1.001、n=3.0較合理。

2.3.3 理論公式優化結果分析

將Ⅲ級圍巖斷面ZK30+480、ZK30+590、ZK30+905和Ⅳ級圍巖斷面ZK31+485、ZK31+560、ZK31+650的監測數據與式(7)計算數據和修正公式(11)計算數據對比分析，如圖12所示。

對圖12中的曲線進行擬合，得到各擬合曲線的方差和相關系數如表4所示。

結果顯示：通過增加擴大收斂函數有效地提高了理論公式的擬合效果(相關系數由原來的0.8提高到0.97)；擬合結果證實了圍巖的變形規律不僅與泊松比有關，還與彈塑性模量、內摩擦角、黏聚力以及爆破參數等有關；同時也驗證了圍巖的質量越差裂隙越多，承載能力越低，空間約束效應越不顯著，開挖過程中圍巖的徑向位移產生的越早，圍巖最終變形越大，達到最終收斂越晚。

表4 圍巖擬合參數Table 4 Fitting parameters of surrounding rock

圖10 試驗儀器及巖樣Fig.10 Uniaxial compression test of rock

圖11 巖樣單軸壓縮σ-ε圖Fig.11 Uniaxial compression test diagram of rock sample

圖12 拱頂位移釋放系數監測與理論擬合圖Fig.12 Monitoring and theoretical fitting diagram of vault displacement release coefficient

2.4 數值模擬及驗證分析

運用FLAC3D建立數值模型，模型具體尺寸：模型寬取42 m，高取35 m，長度取84 m，根據斷面所在位置的地應力情況，模擬開始時在x、y、z方向上分別施加不同的初始應力來模擬開挖前初始地應力平衡，如圖13所示。

運用FLAC3D模擬Ⅲ級和Ⅳ級圍巖的開挖全過程，每次開挖進尺為3.5 m，整個過程共循環開挖24次，并監測隧道斷面A-A/處拱頂的徑向位移，其監測斷面位移變形過程圖如圖14所示。

監測結果顯示：掌子面在距監測面5倍洞半徑時，監測斷面上的監測點開始出現徑向位移，但位移值很小；隨著掌子面的推進，監測斷面上的測點圍巖位移迅速增大，隨后逐漸趨于穩定；分析Ⅲ級圍巖在采用長臺階法開挖時測得斷面ZK30+480、ZK30+590、ZK30+905的拱頂最終沉降量分別為19.1、19.7、20.7 mm；Ⅳ級圍巖在采用CRD工法開挖時測得斷面ZK31+485、ZK31+560、ZK31+650的拱頂最終沉降量分別為18.6、21.5、24.1 mm；其上述模擬結果與現場實際監測數據較接近，證實了現場隧道開挖采用工藝的有效性。

圖13 隧道模型及監測斷面示意圖Fig.13 Schematic diagram of tunnel model and monitoring section

圖14 監測斷面拱頂位移模擬變化圖Fig.14 Simulated change diagram of vault displacement of monitoring section

將模擬數據與監測數據和理論計算數據對比分析，獲得不同斷面處的位移釋放系數變形曲線，如圖15所示。

分析不難看出修正后的式(11)能夠更好地與實際監測數據和模擬數據相吻合，其曲線變化形式也得到改進，能夠更真實地應用到實際工程中；進一步證實了圍巖的位移釋放系數的變化規律不僅與泊松比有關，還與彈塑性模量、內摩擦角、黏聚力以及爆破參數等有關。

3 初支時機預測

3.1 理論分析

掌子面的時空效應可劃分為空間效應和時間效應2個階段[24](圖16)，“空間效應”主要作用在S1段；時間效應則對應圍巖的流變性，主要體現在S3

圖15 拱頂位移釋放系數模擬與理論擬合圖Fig.15 Simulation and theoretical fitting diagram of displacement release coefficient of arch crown

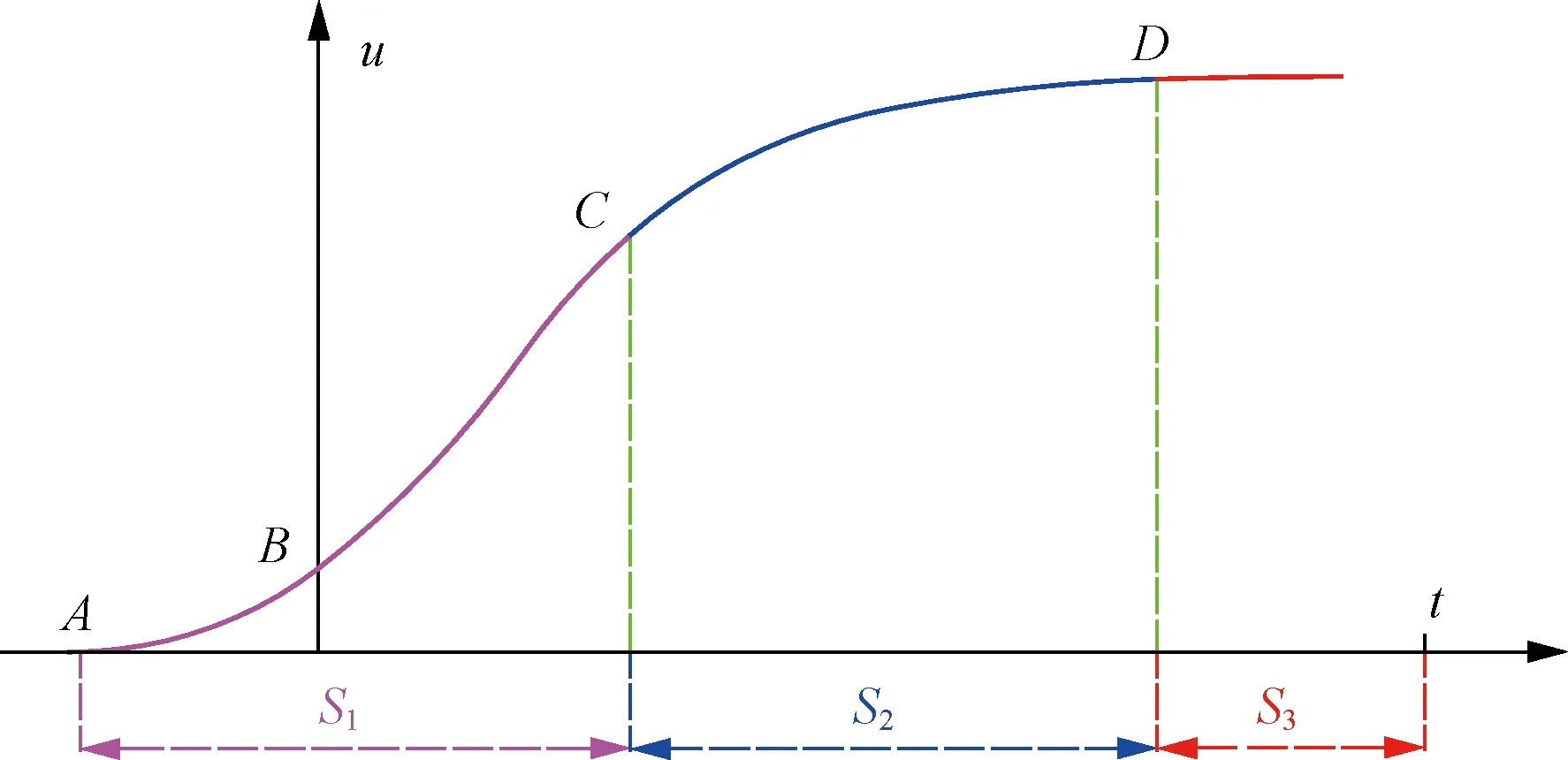
圖16 圍巖變形全過程曲線Fig.16 Whole process curve of surrounding rock deformation

段。然而隧道初支一般在BC段內完成，CD段主要是圍巖與支護結構相互作用的平衡穩定階段。

由于軟巖隧道支護設計采用的本構關系與硬巖隧道支護設計采用的本構關系截然不同[12-13，25]，因硬巖隧道設計的支護時機是不允許圍巖出現塑性變形(圍巖一旦進入塑性狀態就喪失承載能力)，而軟巖隧道具有相反的獨特之處：因軟巖本身具有巨大的塑性能(如膨脹變形能、高應力變形能等)，如果通過塑性變形有效地釋放出來，能夠很好地確保軟巖自穩承載能力。

基于軟巖獨特的彈塑性變特性，在考慮空間效應的作用下其支護結構施作時機可通過圍巖位移釋放系數和位移增量變化來判斷：在此提出掌子面附近圍巖位移增量出現陡增點時，所對應的位移釋放系數值，即為支護結構施作的最佳時機。

3.2 初支時機選擇

依據上述理論分析，隧道在開挖過程中位移增量曲線出現陡增點時所對應的位移釋放系數值即為最佳支護時機；根據數值模擬和現場監測拱頂位移增量變化曲線顯示，如圖17和圖18所示。

Ⅲ級圍巖在長臺階法施工工藝施作下距監測面的距離比在0～0.5位移增量達到最大值；采用線性插分法可求得此時所對應的位移釋放系數為λ(x)=0.81，將求得的位移釋放系數帶入修正后的式(10)可得：x/R=0.35，即隧道開挖后由于掌子面“空間效應”的作用，可確保在距掌子面x=2.45 m處開始施作支護的安全性。

圖17 模擬斷面位移增量曲線圖Fig.17 Displacement increment curve of simulated section

圖18 實測斷面位移增量曲線圖Fig.18 Displacement increment curve of measured section

同理分析可求得Ⅳ級圍巖在采用CRD工法開挖下距監測面的距離比在0～0.5位移增量達到最大值，采用線性插分法可求得此時所對應的位移釋放系數為λ(x)=0.76，代入修正后的式(10)可得x/R=0.25，即在距掌子面x=1.75 m處開始施作支護是安全的。

實際施工過程中考慮到調動圍巖自承載能力，支護結構與掌子面實行錯步開挖推進；其中III級圍巖在采用長臺階法施工時，量測到支護結構距上導掌子面約2.5 m，IV圍巖在采用CRD工法施工時，量測到支護結構距上導掌子面約1.5 m，并觀察發現圍巖未見明顯裂縫和松動等現象；其結果與采用理論修正公式求得的支護結構設置距離有很好的一致性，證實了理論公式推導出最佳支護時機選擇的合理性；現場支護結構與掌子面設置距離，如圖19所示。

4 結論

實際工程對支護理念往往只注重片面地提高支護結構強度，忽略合理施作支護結構的時機；然而合理確定支護施作時機，是確保圍巖-支護結構體系共同響應的基礎。

圖19 實測支護-圍巖間距圖Fig.19 Measured support surrounding rock spacing diagram

(1)摒棄了前人一貫依據工程經驗和模擬等方法，通過對比斷面監測數據與理論計算數據，發現Unlu等[23]推導的圍巖縱向變形曲線方程在x≥0段偏差較大，在綜合考慮彈塑性模量、泊松比、黏聚力、內摩擦角、爆破參數等因素的影響，提出增加擴大收斂函數進行優化改進。

(2)通過試驗和擬合給出了擴大收斂函數的相關參數，并指出優化改進的圍巖縱向變形曲線方程，主要適合于軟巖或較破碎巖體，特別是隧道開挖后圍巖變形破壞較嚴重，相關參數變化較大的巖體。

(3)將現場監測數據、原理論公式求解數據、優化改進理論公式求解數據以及數值模擬，進行對比分析，證實了改進后的圍巖縱向變形曲線方程能更好地與其相吻合，進一步證實改進后的圍巖縱向變形曲線方程更具有合理性和實用性。

(4)從軟巖與硬巖能量釋放和變形特性出發，依據軟巖具有巨大的塑性能，使其通過塑性變形有效地釋放出來，能夠更好地發揮其自穩承載能力；提出位移增量出現陡增點時的位移釋放系數值為施加支護的最佳時機，得出Ⅲ級圍巖在長臺階法施工施作時，距掌子面x=2.45 m處開始施作支護為最佳，Ⅳ級圍巖在采用CRD工法施作時，距掌子面x=1.75 m處開始施作支護為最佳。