基于ELM-SVR模型的裝備關鍵部件壽命預測
范小虎, 趙愛罡, 許強, 葛春, 李瑞帥, 張猛, 劉茜萱
(火箭軍士官學校, 青州 262500)
現代化精導武器裝備中,兼有導航制導、環境感知、自主決策及毀傷評估等作戰任務,主要由一些傳感器、測量裝置、導航裝置、執行機構等關鍵部件組成。武器裝備長時間服役時,其中各關鍵部件是決定武器系統壽命的主要原因,因此,研究眾多關鍵部件的剩余壽命預測,不僅能夠預估武器系統的可靠性,降低發生事故的概率,而且可為科學制訂武器系統維護保養計劃提供參考和依據,為科學合理地使用武器系統提供有力保障。
剩余使用壽命預測方法中,基于機器學習的數據驅動預測方法是目前行業研究的主流方向,眾多學者對剩余使用壽命預測進行了深入研究。裴洪等[1]分析了基于機器學習的剩余壽命預測方法,根據機器學習模型隱層神經元的層數,分為淺層機器學習模型和深度學習模型。周俊[2]將數據驅動的預測方法細分為基于人工智能的方法、基于隨機過程的方法、基于時間序列分析的方法和基于狀態估計的方法,并將RUL(remaining useful life)預測方法進行融合研究。時間序列預測[3]方法主要有移動平均自回歸(autoregressive integrated moving average, ARIMA)[4]模型、支持向量回歸機(support vector regression, SVR)[5-6]模型、極限學習機(extreme learning machine, ELM)[7-9]模型、深度學習[10-11]模型等,一階灰度[GM(1,1)]模型為指數模型,可描述時間序列長期的變化趨勢,對局部劇烈的變化無法預測;ARIMA[12]模型可以擬合序列相鄰之間的相關性,但對序列要求比較苛刻,要求序列是平穩性;SVR可以對序列核變換之后的線性關系進行描述,但是對非線性變化預測不佳;ELM[13]訓練簡單,對非線性變化擬合效果好,但隨機參數的選擇也一定程度影響了預測精度。
武器裝備關鍵部件較多,因受環境、震動、運動等因素影響,即使屬于同廠家同批次產品,其綜合性能指標也可能是不同的。綜合性能指標序列的平穩性、線性及變化趨勢等特性均無法預知,因此無法直接使用ARIMA及GM(1,1)模型,ELM及SVR單一模型對非線性序列的預測精度不高,因此,現將ELM模型與SVR模型融合建立ELM-SVR模型,對ELM模型的神經元輸出使用核函數進一步將特征映射到高維空間,提高特征的辨識度,輸出擬合采用SVR[14]模型的軟間隔函數,以進一步提高預測精度。
1 ELM模型
ELM相比傳統的BP神經網絡,將參數迭代優化過程轉化為隨機生成隱層網絡權值和神經元偏置,線性規劃問題,降低了參數優化不收斂的風險和難以調節的難度。網絡結構如圖 1所示。


ai,j、bj為隨機生成權值和神經元偏置;βj為線性規劃參數圖1 ELM模型網絡結構Fig.1 ELM model network structure
(1)

GβELM=Y
(2)
式(2)中:G為神經元矩陣;Y為輸出向量;βELM為輸出權值。其值分別為
(3)
Y=[y1y2…yN]T
(4)
βELM=[β1β2…βL]T
(5)
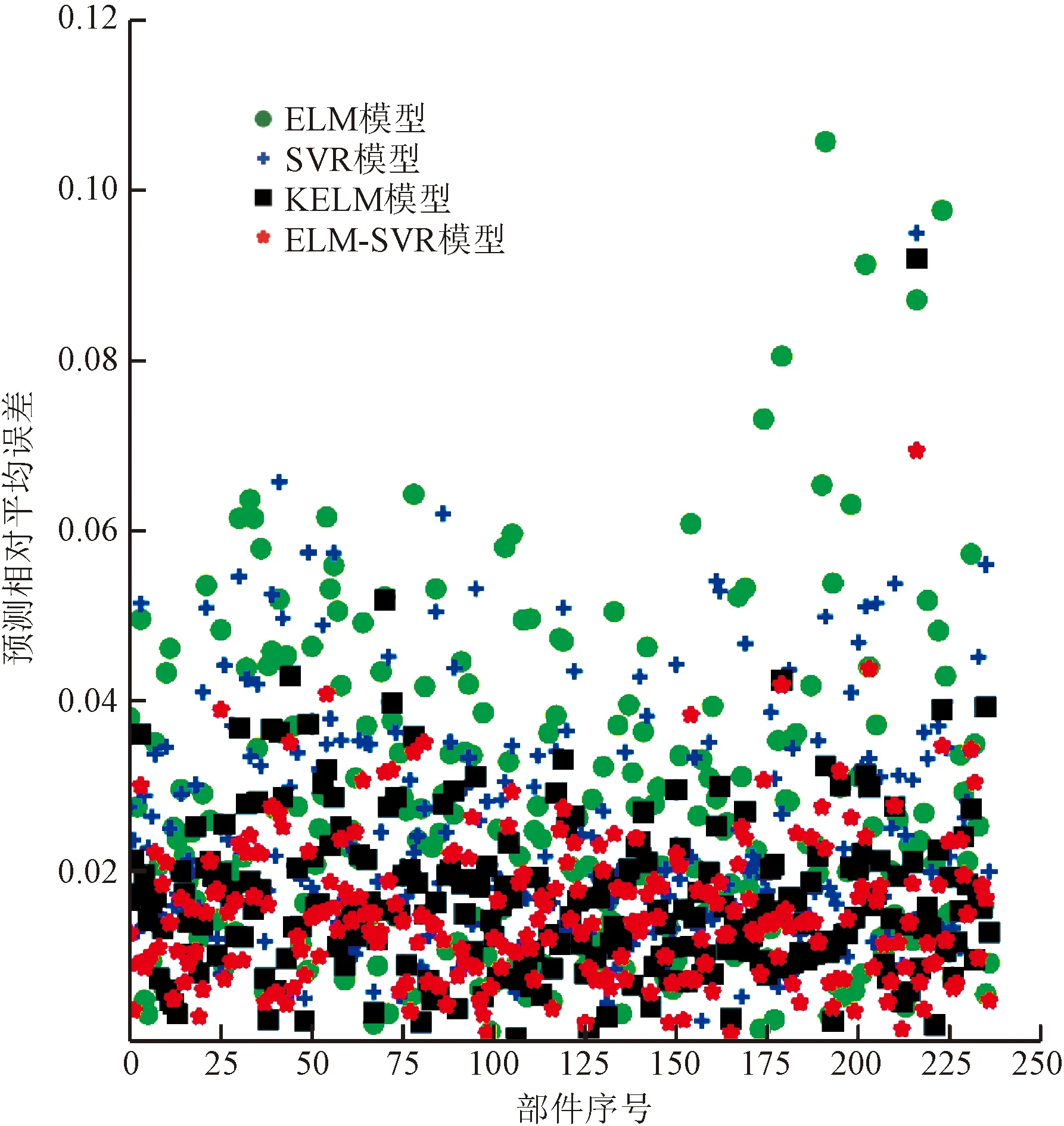
實際應用中,隱層神經元數量一般小于訓練樣本數量,即L βELM=G?Y (6) 式(6)中:G?為矩陣G的廣義逆,為防止出現相同訓練樣本導致廣義逆矩陣不穩定的情況,引入正則化系數λ及單位矩陣I,則網絡輸出權值的最小二乘解為 βELM=GT(GGT+I/λ)-1Y (7) 為進一步提高特征的區分度,在ELM模型的基礎上,使用核函數對神經元矩陣進行處理,將神經元矩陣G中的行特征,即將經過神經元激活函數映射后的特征,再次向更高維空間映射,則式(3)中神經元矩陣變為 (8) 相應的式(7)中GGT換為HHT,稱為核矩陣,其表達式可寫為 (9) 式(9)中:φ[f(xi)]=φ[f(a1xi+b1],…,f(aLxi+bL)],因為高維空間的向量內積可使用低維空間的核函數等價計算,核函數為 κ[f(xi),f(xj)]=<φ[f(xi)],φ[f(xj)]> =φ[f(xi)]Tφ[f(xj)] (10) 經過以上分析,KELM模型的輸出權值計算公式為 βKELM=HT(ΩKELM+I/λ)-1Y (11) 式(11)中:H的映射φ(·)無需確定具體形式,在預測中使用核函數替代。 KELM模型求解步驟為:①隨機生成輸入權值ai和隱層神經元偏置系數bi,i=1,2,…,L,選定核函數類型κ(·);②計算隱層神經元矩陣G;③計算核矩陣ΩELM;④輸出預測值計算公式為yKELMpredict={κ[f(x),f(x1)],…,κ[f(x),f(xN)]}1×N×(ΩKELM+I/λ)-1Y。 h(x)=wTφ(x)+b (12) 式(12)中:w、b為模型的系數及偏置;φ(·)為映射函數,將低維特征映射到高維空間,以便增強特征的區分度。SVR模型容許預測值h(x)與真實值yi之間存在偏差ε,預測值超出容許偏差的樣本值,距離超平面距離越近精度越高,SVR最優化問題可描述為 (13) (14) 具體求解過程中,給定嵌入維M,將時間序列生成訓練樣本集,給定待預測特征向量x,SVR模型求解步驟如下。 步驟1確定參數。C、ε、γ需要根據訓練樣本的擬合結果進行迭代選定最優參數,核函數選擇RBF函數,表達式為 κ(xi,xj)=exp(-γ‖xi-xj‖2) (15) 步驟3對新特征向量x預測。按照式(14)計算預測值。 ELM模型屬于單隱層神經網絡,其訓練過程為:隱層神經元輸入權值及偏置為隨機產生,經過L個神經元激活后,輸入的M維特征向量映射為L維特征向量,增加了特征維度,特征之間的區分度增強了,有利于分類和回歸問題。ELM模型輸出網絡權值以L維特征向量為輸入,以實際輸出yi為響應,建立線性回歸,以均方誤差為優化函數,使用最小二乘法求得輸出網絡權值βELM。 ELM-SVR模型中特征向量映射到高維空間,將最后的線性回歸模型使用SVR回歸代替。即式(12)變為 h(x)=wTφ(f(x))+b (16) 式(16)中:f(x)=[f(a1xi+b1),…,f(aLxi+bL)]T,即經過ELM隱層神經元激活后的特征向量,優化過程是相同的,相應的預測表達式為 (17) ELM-SVR模型使用SVR回歸代替線性回歸,這樣處理避免了對所有訓練樣本計算損失,對符合預測精度的樣本即偏差ε內的樣本不計算損失,對擬合偏差在ε以外的樣本計算損失,優化模型的參數,突出某些樣本的重要性,這是支持向量的含義,在預測特征向量時,可只與支持向量計算核函數,降低了計算量,增強了模型的泛化能力。 ELM-SVR模型的訓練復雜度較高,預測時間均為毫秒級。模型訓練的時間復雜度與SVR相同,因為 ELM模型神經元輸出的復雜度為O(nLM),其中n為樣本數量,L為神經元個數,M為嵌入維的維數,本應用中M、L一般較小,故ELM模型時間復雜度一般為O(n)。SVR典型訓練算法的時間復雜度為O(N3+nN2+NnM),其中N是支持向量的個數,n是訓練集樣本的個數,M是每個樣本的維數。故ELM-SVR模型的訓練復雜度約為O(N3+nN2)。 圖2 ELM-SVR模型流程圖Fig.2 ELM-SVR model flow chart 某批次武器裝備共有關鍵部件230個,在使用期間,連續執行任務,每隔15 d進行一次全面測試,結合測試數據及相應標準,最終形成綜合性能指標,當指標大于0.7時,壽命終止。 如圖 3所示,為230個同類關鍵部件綜合性能指標全壽命曲線,每條曲線變化趨勢相似,但局部變化不同,變化快慢差異明顯,導致同批次關鍵部件,不同使用環境下,壽命也是不同。 圖3 關鍵部件綜合性能指標全壽命曲線Fig.3 Comprehensive performance index’s full life curve of key components 如圖 4所示,隨機3個關鍵部件的綜合性能指標曲線,在曲線前半段,曲線大致在[0.1,0.3]范圍內震蕩,是穩定使用期階段;在某次測試之后,指標逐漸升高,直至壽命終止,進入了急速退化期階段;急速退化期中的曲線變化步長逐漸變大,某些測試周期會出現下降的反復現象。根據以上分析,對剩余使用壽命相關性最大的是急速退化期,所以需要對急速退化期實現自動提取,簡化預測模型,對剩余使用壽命進行預測。根據綜合性能指標曲線特點,如圖 4所示,采用歸一化曼哈頓距離最大值方法提取急速退化期,提取步驟如下。 (1)選取終點。在綜合性能指標曲線上任取大于0.4的一點為終點B,坐標(xB,yB)。 LX為曲線上任一點距離起點A的水平距離(即X軸的跨度); LY為曲線上任一點距離終點B的垂直距離(即Y軸的跨度)圖4 急速退化期示意圖Fig.4 Schematic diagram of rapid degeneration period (2)計算曲線上任一點的歸一化曼哈頓距離。起點為A點,坐標為(xA,yA)=(0,0.2),點C為曲線AB中間任一點,坐標為(xC,yC),則歸一化曼哈頓距離為: (18) 式(18)中:α為權重系數,取值一般為[0.5,0.65]。 (3)確定歸一化曼哈頓距離最大的點為急速退化期起點。 如圖 4所示為隨機3個關鍵部件的綜合性能指標,虛線標注的為使用曼哈頓距離最大值方法提取的急速退化期起點,可以看出能夠自動捕捉曲線的拐點,急速退化期內曲線趨勢走向明顯,變化模式相對簡單,降低了預測難度。 可靠性要求極高的武器裝備系統長期預測不確定因素較多,一般結合定期測試數據進行短期預測。為驗證預測模型的效果,將全壽命綜合性能指標序列的最后兩個數據作為驗證數據,序列其余部分作為訓練樣本,對模型參數進行優化。 ELM模型參數包括:嵌入維大小、神經元數量、神經元激活函數,根據多樣本擬合的經驗值,神經元激活函數為sigmoid函數,嵌入維范圍:[2,6],神經元數量范圍:[5,20],每個綜合性能指標搜索最佳參數。SVR模型參數采用網格化搜索機制,每個指標序列的嵌入維與對應的ELM模型一致,核函數取值為RBF函數,容許誤差ε取值為[0.000 05,0.000 1,0.000 2],參數C的取值為[0.5,1.0,5.0,10],參數γ取值為[0.5,1.0,1.5],在參數的組合中以擬合誤差最小為準則選擇最佳參數組合。KELM的核函數采用RBF函數,其余參數與對應的ELM模型一致。為對比模型預測效果,對每個指標序列進行預測時,ELM-SVR模型均采用與ELM、SVR模型一致的參數。 圖5為4種模型對關鍵部件19、146、212急速退化期的預測結果對比圖,從圖5可以看出,4種預測模型均能夠擬合曲線的變化趨勢,但在局部劇烈變化處,4種模型擬合均存在滯后現象,在曲線平穩段誤差較小,影響剩余使用壽命的最后兩個數據一般變化比較平緩,預測精度較高。4種模型對比,關注最后兩個預測數據,特別是圖5(b)和圖5(c)中,ELM-SVR預測精度最高,其次為KELM模型,ELM與SVR模型在圖5(b)中預測值與真值誤差較大。 圖6為ELM-SVR模型對多個關鍵部件綜合性能指標序列的擬合、預測曲線,黑色為樣本真值,紅、綠、藍色曲線為ELM-SVR模型的擬合、預測曲線(后兩個數據為預測值)。可以看出在達壽指標0.7附近曲線變化較為平緩,ELM-SVR模型預測精度比較高,未影響剩余使用壽命的預測精度。 圖5 4種模型對某些部件的預測結果對比Fig.5 Comparison of the prediction results of the four models for certain parts 圖6 ELM-SVR模型的預測結果Fig.6 Prediction results of ELM-SVR model 在230個關鍵部件綜合性能指標的擬合與預測中,與ELM、SVR、KELM模型相比,擬合精度分別提高了30.61%、20.93%、5.56%,預測精度分別提高了57.14%、44.44%、11.76%。ELM-SVR對多個關鍵部件綜合性能指標序列的擬合、預測精度比較一致,表明ELM-SVR模型具有一定的魯棒性。 圖7為4種模型對230個關鍵部件綜合性能指標序列的預測相對平均誤差。ELM模型與SVR模型的相對平均誤差較大,KELM模型與ELM-SVR模型預測相對誤差較小,均處于點圖的下方,ELM-SVR預測相對平均誤差更為集中,對全部關鍵部件預測相對平均誤差集中在0.02以下,表明了ELM-SVR模型的魯棒性。 圖8為4種模型對達壽時綜合性能指標的預測對比,即對樣本序列最后一個值的預測。從圖8可以看出,黑色曲線的SVR模型比真值偏大,藍色曲線的ELM比真值偏小,KELM模型預測值比真值稍大,ELM-SVR模型預測值與真值最為接近。 對于序列末位達不到0.7的,繼續逐步預測,直至末位數據大于0.7為止。計算樣本真值、4種模型預測序列綜合性能指標大于0.7時的檢測次數,次數減1即為測試次數,使用壽命計算公式為 S(i)={j-1|xi,j≥0.7}×15,i∈[1,237] (19) 式(19)中:S(i)為對應關鍵部件的使用壽命;xi,j為第i個序列的第j次測量的綜合性能指標。 綠色為樣本真值圖7 4種模型的預測相對平均誤差對比Fig.7 Comparison of the relative mean error of prediction of the four models 圖8 4種模型達壽指標對比Fig.8 Comparison of life expectancy indicators of four models 表1 4種模型對綜合性能指標、壽命預測的相對平均誤差Table 1 Relative average error of four models for comprehensive performance index and RUL prediction 表1為4種模型對綜合性能指標擬合與預測的相對平均誤差,最終使用壽命預測的相對誤差,ELM-SVR模型在3種對比項目中均為最優。ELM-SVR模型將輸入特征兩次向高維空間映射,設置容許誤差,只對偏離回歸值較大的支持向量計算損失函數,這種組合模型與ELM、SVR、KELM模型相比,能夠顯著提高擬合與預測精度,實驗仿真驗證了ELM-SVR模型的泛化能力與魯棒性。 針對復雜武器裝備的關鍵部件較多,其綜合性能指標數據變化各異,為進一步提高壽命預測精度,提出了通過歸一化曼哈頓距離最大值法提取影響壽命的急速退化期數據,并采用ELM-SVR模型對多個關鍵部件剩余使用壽命進行預測,通過對230個關鍵部件的綜合性能指標進行建模預測,可得到如下結論。 (1)采用歸一化曼哈頓距離最大值法提取綜合性能指標的急速退化期,能夠準確捕捉綜合性能指標的變化拐點,精準識別急速退化階段,有利于提高模型對剩余使用壽命的預測精度。 (2)ELM-SVR模型能夠融合ELM、SVR模型的優勢,通過使用神經元激活函數與核函數實現兩次將輸入特征向高維空間映射,增強了特征的區分度,提高了模型的預測能力。 (3)通過230個關鍵部件綜合性能指標的預測結果,ELM-SVR模型的平均擬合與預測精度最高,與單一模型相比,其魯棒性與泛化能力具有優勢。2 KELM模型
3 SVR模型

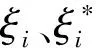

4 ELM-SVR模型
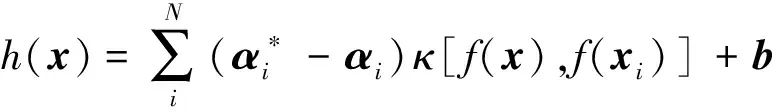

5 關鍵部件剩余壽命預測

5.1 急速退化期提取
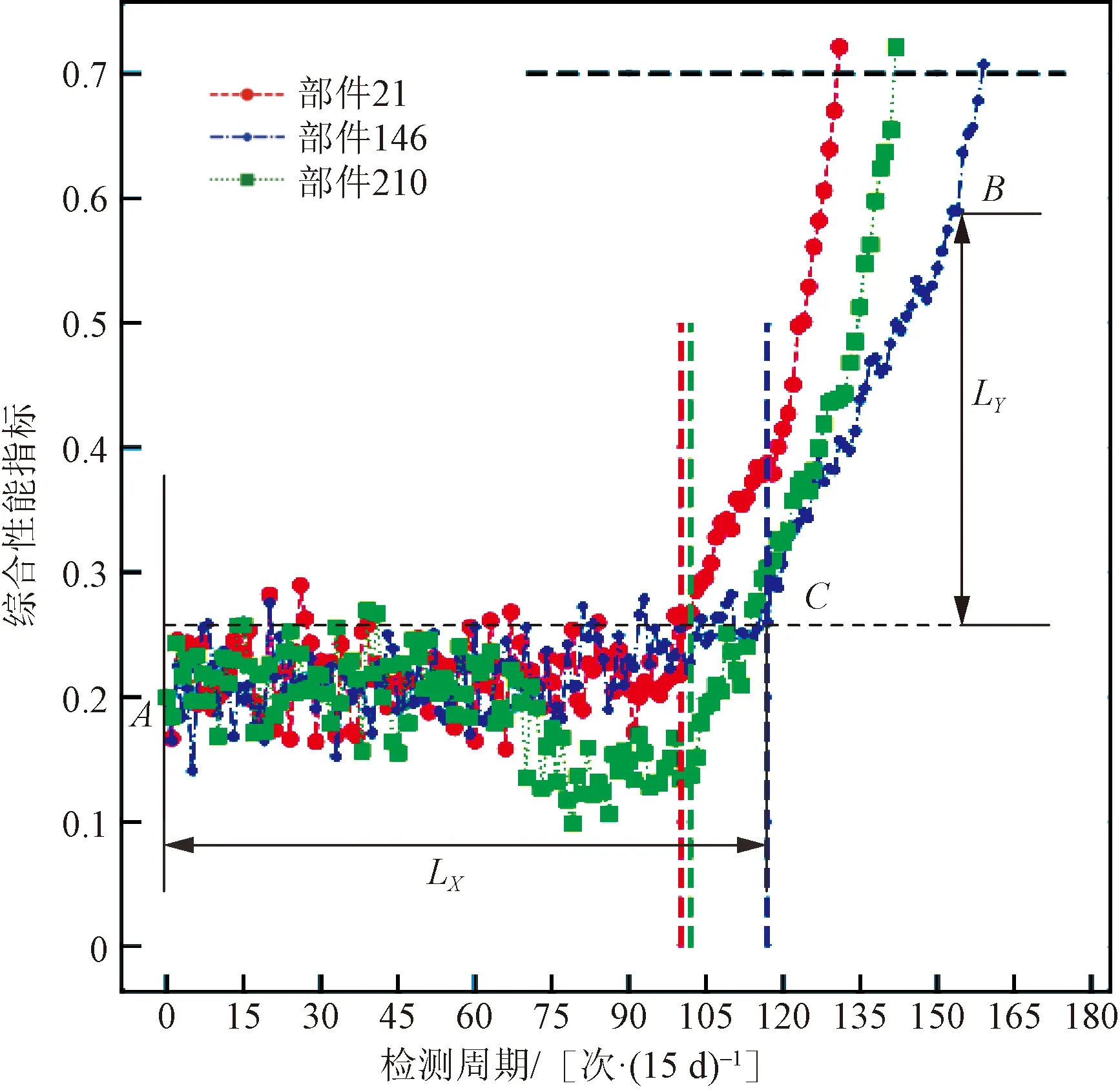
5.2 ELM-SVR模型預測結果
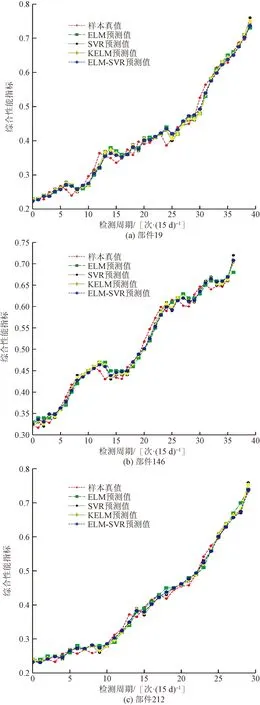

5.3 不同模型預測性能對比


6 結論

