基于改進SAC算法的移動機器人路徑規劃

李永迪，李彩虹，張耀玉，張國勝

（山東理工大學 計算機科學與技術學院，山東 淄博 255049）

0 引言

在移動機器人自主導航中，路徑規劃是一個重要的組成部分，可以描述為在一定的約束條件下，尋找一條從起點到目標點的最優路徑。常見的路徑規劃方法有人工勢場法［1］、A*算法［2-3］、蟻群算法［4-5］、遺傳算法［6］、粒子群優化算法［7］等。這些算法大都需要建立地圖模型，工作在已知環境下；另外在復雜環境中存在運算時間長、迭代次數多以及在未知環境下實時性差或者容易陷入局部最優等問題。

近年來，深度學習（Deep Learning，DL）［8］和強化學習（Reinforcement Learning，RL）［9］成為機器學習領域重要的研究熱點，將深度學習和強化學習相結合的深度強化學習（Deep Reinforcement Learning，DRL）［10］算法在移動機器人路徑規劃中得到了廣泛使用。深度強化學習具有深度學習的感知優勢和強化學習的決策優勢，其中，深度學習負責通過傳感器獲取周圍環境信息來感知機器人當前的狀態信息，而強化學習負責對獲取的環境信息進行探索、做出決策，從而實現移動機器人路徑規劃的智能化需求。

SAC（Soft Actor-Critic）算法是Haarnoja 等［11］提出的一種穩定高效的DRL 算法，適用于現實世界的機器人技能學習并能與機器人實驗要求高度契合，能夠滿足實時性的需求；Haarnoja 等［12］在SAC 算法中加入了熵權重的自動調整，在訓練前期熵的權重較大，在后期逐漸衰減熵的權重，讓智能體收斂更加穩定；De Jesus 等［13］將SAC 算法應用到ROS（Robot Operating System）環境下，實現了移動機器人在不同環境下的局部路徑規劃，但算法存在訓練時間長和環境獎勵稀疏的問題；肖碩等［14］引入智能體通信機制，有效降低了環境不穩定性對算法造成的影響，但樣本利用率低、收斂慢；單麒源等［15］優化了算法的狀態輸入，改善了訓練次數越多獎勵值越低的問題，但應用場景簡單，面對復雜環境算法效率無法保證；胡仕柯等［16］通過在原有算法中引入內在好奇心機制，提高智能體探索能力與樣本利用效率，同樣存在應用場景簡單且收斂速度較慢。

針對上述算法的不足，本文對SAC 算法進行了改進，首先，提出的PER-SAC 算法使用三層全連接神經網絡，通過雷達傳感器獲取環境信息和目標點信息，并且令環境中障礙物的距離信息、機器人的角速度和線速度、機器人與目標點之間的距離和角度，作為網絡的輸入，輸出為機器人的角速度和線速度；進而結合優先級經驗回放（Prioritized Experience Replay，PER），對經驗池中不同樣本的重要程度進行區分，使重要程度較高的樣本更頻繁地回放，進一步提高了原始算法中樣本的利用率，從而進行更有效的學習，提高算法的收斂速度；然后設計改進的獎勵函數，克服環境獎勵稀疏的缺點；此外，設計了不同的仿真環境（無障礙物、離散障礙物和特殊障礙物），提高算法的泛化性；考慮到在不同障礙物環境下實驗的重復性，引入遷移學習，將收斂后的無障礙物模型作為離散型障礙物與特殊障礙物環境的初始化模型，加快算法收斂。

1 SAC算法

SAC 算法使用了AC（Actor-Critic）體系結構［17］。傳統強化學習的目標是使獎勵的期望最大，而SAC 使獎勵期望和熵值同時最大化：

其中：E是當前狀態的回報期望，r是當前狀態的回報值，ρπ為t=0 到T所有的狀態和動作的集合，H是當前動作的熵，τ是溫度系數，π是通過網絡得到的當前狀態的所有動作概率。

SAC 算法為了減小值函數的估計誤差，在Actor-Critic 體系的基礎上增加了價值網絡，由1 個Actor 網絡（策略網絡）和4 個Critic 網絡構成，分別是狀態價值估計V和TargetV網絡，由VCritic 表示；動作-狀態價值估計Q0和Q1網絡，由QCritic 表示。SAC 算法網絡構架如圖1 所示。

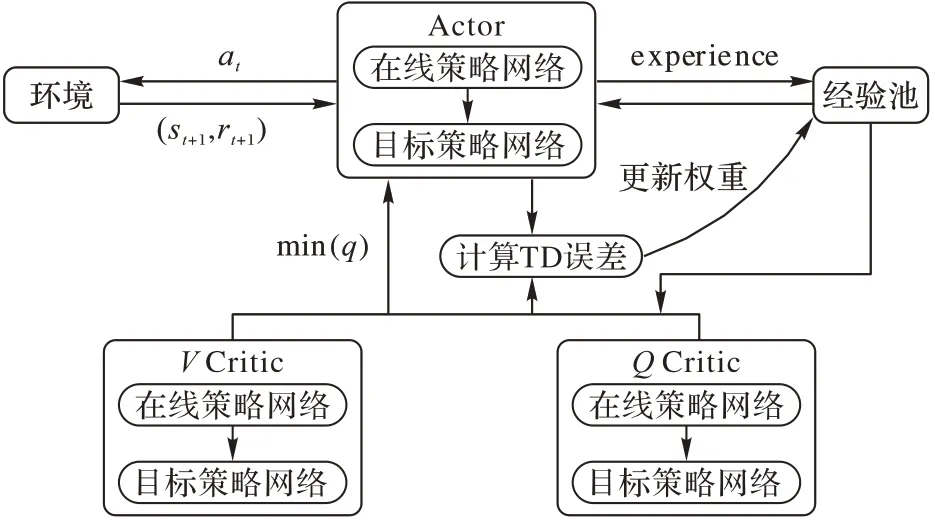
圖1 SAC算法網絡構架Fig.1 Network framework of SAC algorithm

已知一個狀態st，通過Actor 網絡得到所有動作概率π(a|st)，依概率采樣得到動作at∈a，將at輸入到環境中得到st+1和rt+1，獲得1 個experience：（st，at，st+1，rt+1），放入到經驗池中。

在QCritic 網絡中，從經驗池中采樣出數據（st，at，st+1，rt+1），進行網絡參數ω的更新，將動作at的q（st，at）值作為st的預測價值估計，根據最優Bellman 方程得到作為st狀態的真實價值估計：

其中Eπ為當前狀態的累計回報期望。

用均方損失函數作為損失，對QCritic 網絡進行訓練，損失函數定義為：

其中B為從經驗池中取1 個batch 的數據。

在VCritic 網絡中，從經驗池采樣出數據（st，at，st+1，rt+1），進行網絡參數θ的更新，Vcritic 網絡輸出的真實值為：

其中：為Actor 網絡的策略π預測的下一步所有可能動作；lnπ(，θ)為熵。

根據真實值計算Vcritic 網絡的損失：

在Actor 網絡中，進行梯度下降訓練的損失函數定義為：

強化學習通過時序差分（Temporal-Difference，TD）誤差衡量算法修正幅度，采用計算TD 誤差的形式對策略選擇的動作at進行評估：

其中：Q為Critic 的狀態價值，γ為折扣因子。

2 改進SAC算法

為提高訓練速度和穩定性，本文設計了PER-SAC 算法，將優先級經驗回放引入SAC 算法中，使從經驗池中等概率隨機采樣變為按照優先級采樣，增大重要樣本被采樣的概率。利用重要性采樣權重來修正優先回放引入的誤差，并更新網絡的損失函數，減少模型的錯誤率。PER-SAC 算法包含了網絡結構、獎懲函數、連續的狀態空間和動作空間的設計。

2.1 網絡結構

PER-SAC 算法所采用的神經網絡有14 個輸入和2 個輸出，如圖2 所示。

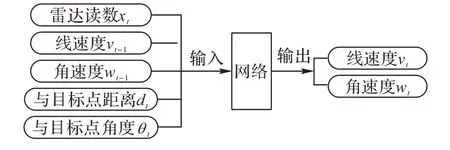
圖2 網絡的輸入和輸出Fig.2 Network input and output

網絡的輸入包括：雷達10 個方向上的讀數xt，機器人的線速度vt-1和角速度wt-1，機器人的相對位置與目標點的標量距離dt和角度θt；網絡的輸出為機器人的線速度vt和角速度wt。

SAC 網絡結構包括策略網絡（Actor）、Q網絡（QCritic）和價值網絡（VCritic）三個部分，如圖3 所示。

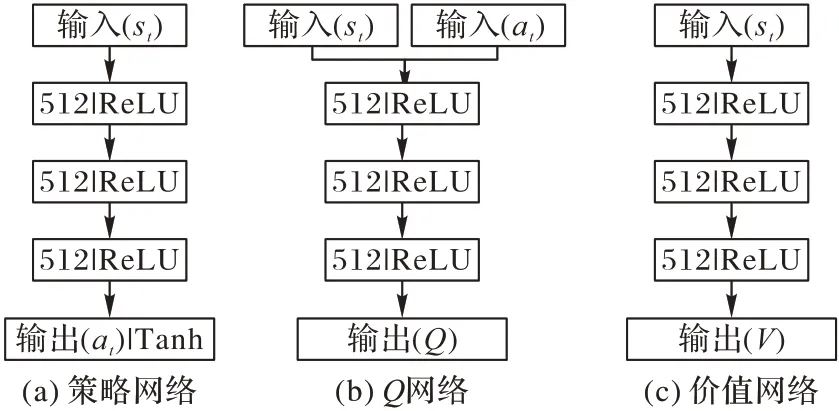
圖3 SAC網絡結構Fig.3 SAC network structure

策略網絡的輸入是機器人在環境中的當前狀態；隱藏層是3 個具有512 個節點的全連接層；輸出層生成發送給機器人要執行的動作。

Q網絡、價值網絡和策略網絡的隱藏層相同。Q網絡給出機器人當前狀態和動作的Q值，而價值網絡預測當前狀態值。

2.2 結合優先級經驗回放

優先級經驗回放賦予每個樣本一個優先級。從經驗池采樣時，使優先級越高的樣本被采樣的概率越大，提高訓練速度，并引入SumTree 來存儲樣本的優先級。

樣本的優先級用TD 誤差定義。TD 誤差越大，優先級越高。TD 誤差δt的計算如式（7）所示，樣本抽取的概率定義為：

其中：a用于對優先程度的調節；pi=|δi|+ε是第i個樣本的優先度，δi是第i個樣本的TD 誤差，加入ε用于避免概率為0。

計算TD 誤差時要考慮SAC 算法中3 個網絡的情況，由于Q網絡和價值網絡輸出的值遠大于策略網絡的值，將3 個網絡的誤差直接相加將導致策略網絡的誤差對總誤差影響較小，因此引入調整系數Tα和Tβ對Q網絡和價值網絡的值進行調整：

由于優先級經驗回放改變了樣本采樣方式，因此使用重要性采樣權重來修正優先回放引入的誤差，并計算網絡進行梯度訓練的損失函數，減小模型的錯誤率。重要性采樣權重計算如下：

其中選取了樣本j的權重wj，并進行歸一化處理，方法是除以所有樣本中權重最大的樣本i，用maxi（wi）表示；N為樣本容量；β是wj的調整系數。

最后使用重要性采樣權重對Q網絡和價值網絡的損失函數進行更新。對式（3）和（5）的更新如下：

2.3 連續的動作空間和狀態空間設計

設計恰當的連續狀態空間和動作空間作為神經網絡的輸入和輸出，通過傳感器返回周圍環境信息。

狀態空間是對智能體所處環境的反饋，是智能體選擇動作空間的依據。機器人搭載的激光雷達，探測范圍為360°，探測距離為3.5 m。考慮到機器人不后退、雷達數據多和計算量大的問題，只使用機器人前方180°的探測范圍和10 個方向上的雷達數據。激光雷達數據的采集方向設置結構如圖4 所示。

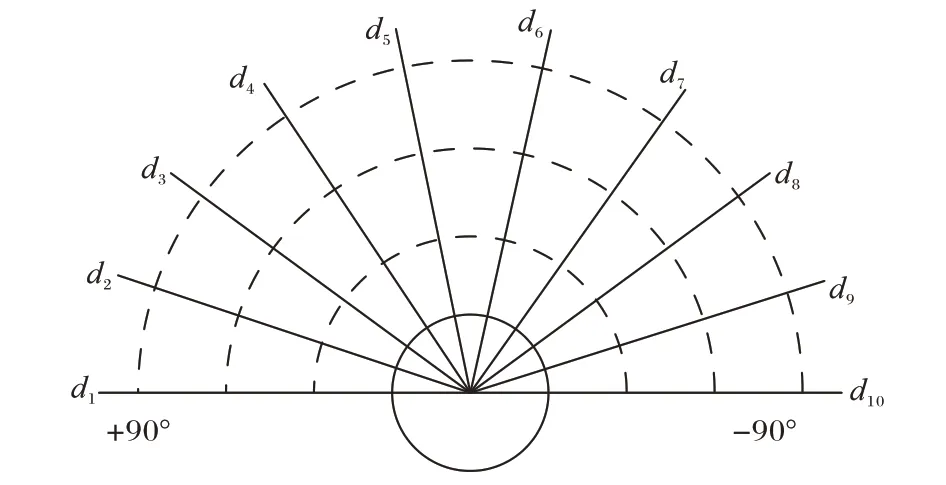
圖4 激光雷達數據采集結構Fig.4 Lidar data acquisition structure

機器人的位姿信息由10 個方向雷達返回的最近障礙物的距離信息di以及機器人與目標點之間的距離Dg和角度θg組成，所以移動機器人狀態空間sj定義為：

機器人運動學模型使用的是Turtlebot3 的Burger 版本，運動參數包含線速度［vmax，vmin］、角速度［wmax，wmin］、最大加速度a。線速度的取值范圍為［0.0，2.0］，單位m/s；角速度的取值范圍為[-2.0，2.0]，單位rad/s。動作空間定義為線速度v和角速度w。

2.4 獎懲函數設計

獎懲函數的設計決定在某一狀態下移動機器人執行一個動作的好壞程度。通過設計一種連續性獎懲函數來解決獎勵稀疏問題。獎懲函數如下：

其中：rarrival表示到達目標點的正向獎勵；dt表示當前時刻機器人到目標點的距離；dt-1表示上一個時刻機器人到目標點的距離；cd表示到達目標點的閾值，小于此值代表到達了目標點；rcollision表示碰到障礙物的負獎勵；minx表示激光雷達的最小距離；co表示碰撞障礙物的安全距離，低于這個值表示觸碰障礙物；cr1和cr2是設置的兩個獎勵參數。

如果機器人通過閾值檢查到達目標，則給予正獎勵；如果通過最小距離讀數檢查與障礙物碰撞，則給予負獎勵。兩種情況都足以結束訓練。否則，獎勵是基于從目標到最后一個時間步的距離差(dt?1?dt)。如果差值是正的，獎勵等于經過的距離乘以參數cr1，否則乘以參數cr2。這種措施激勵移動機器人更接近目標位置，并鼓勵其避開環境中的障礙物。

2.5 遷移學習

局部路徑規劃中的大部分任務存在相關性，在不同地圖環境中利用參數遷移來初始化相關任務中的參數，可以加快移動機器人在不同場景下策略的學習。

首先加載預訓練模型，獲取全部的模型參數。通過隨機初始化訓練獲得趨向目標點的模型參數ωi，將ωi初始化為離散場景ωs和特殊障礙物場景的模型參數ωt，完善避障規則vs與vt，實現局部路徑規劃。本文所設計的遷移學習框架如圖5 所示。

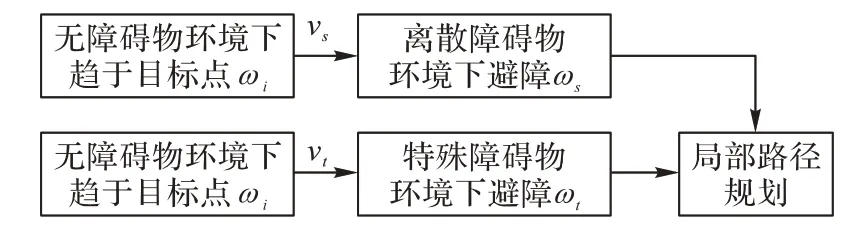
圖5 遷移學習結構Fig.5 Transfer learning structure

3 算法仿真

基于Python 語言，驗證所設計的PER-SAC 算法完成移動機器人局部路徑規劃任務的有效性。在ROS 平臺上利用Gazebo 搭建4 種仿真環境（無障礙物、離散型障礙物、一型障礙物和U 型障礙物環境）來進行PER-SAC 算法和原始SAC 算法的對比實驗。

為了更清晰地觀察仿真結果，將繪制兩種算法訓練的每輪平均回報值對比圖。在Rviz 中，機器人初始位置為起點，方框代表目標點，圓柱體代表障礙物，實線代表機器人的運行軌跡。實驗模型部分參數設置如表1 所示。

表1 仿真參數設置Tab.1 Simulation parameter setting

3.1 無障礙物下的仿真

Gazebo 中無障礙物仿真環境和移動機器人如圖6 所示，在5 m×5 m 的范圍內隨機生成目標點進行訓練。

圖6 無障礙仿真環境Fig.6 Obstacle-free simulation environment

根據設定的參數，移動機器人初始階段在無障礙物環境中訓練，達到預設訓練次數后，抽取批量經驗進行學習，在探索率上升到預設峰值后，探索率保持不變，繼續訓練到預訓練次數，輸出每輪的平均回報值（一輪中的回報值除以本輪步數），如圖7 所示。從圖7 中可以看出，PER-SAC 算法的平均回報值在30 輪左右開始上升，說明算法開始收斂，收斂速度明顯快于原始SAC 算法，而收斂后的PER-SAC 算法相較于原始算法更穩定。

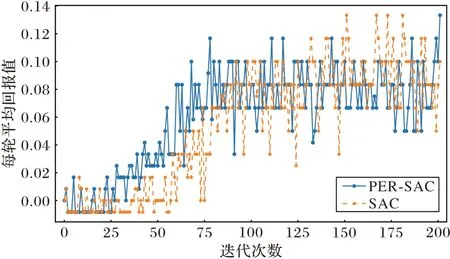
圖7 無障礙環境下每輪的平均獎勵對比Fig.7 Comparison of average reward per round of obstacle-free environment

用兩種算法收斂后模型進行路徑規劃，起點為（1，0.6），終點為（1.2，1.2），并且在Rviz 中繪制路徑，規劃結果分別如圖8（a）和（b）所示。PER-SAC 算法從起點到終點所用步數為115，原始SAC 算法為118，兩種算法的路徑基本一致，PER-SAC 算法路徑略短。

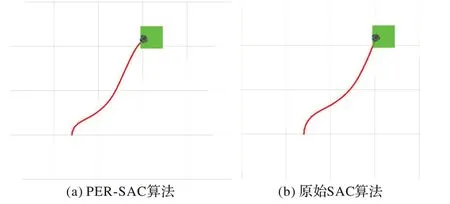
圖8 無障礙環境下的路徑規劃Fig.8 Path planning in obstacle-free environment

3.2 離散障礙物下的仿真

Gazebo 中離散障礙物環境和移動機器人如圖9（a）所示，在Rviz 中如圖9（b）所示。起點為機器人初始位置，坐標為（-2，-2），目標點坐標為（2，1）。

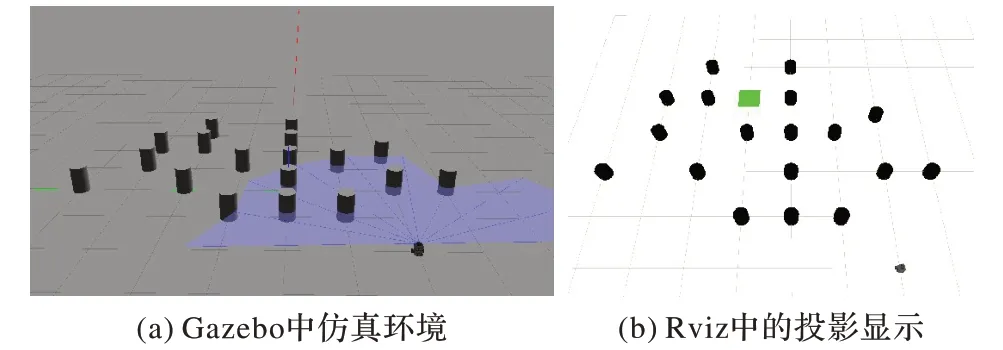
圖9 離散障礙物仿真環境Fig.9 Discrete obstacle simulation environment

利用遷移學習將兩種算法在無障礙物環境下訓練好的模型遷移到7 m×7 m 的離散障礙物環境中作為初始訓練模型，各進行200 輪，每輪500 步的訓練后，輸出每輪平均回報值，如圖10 所示。

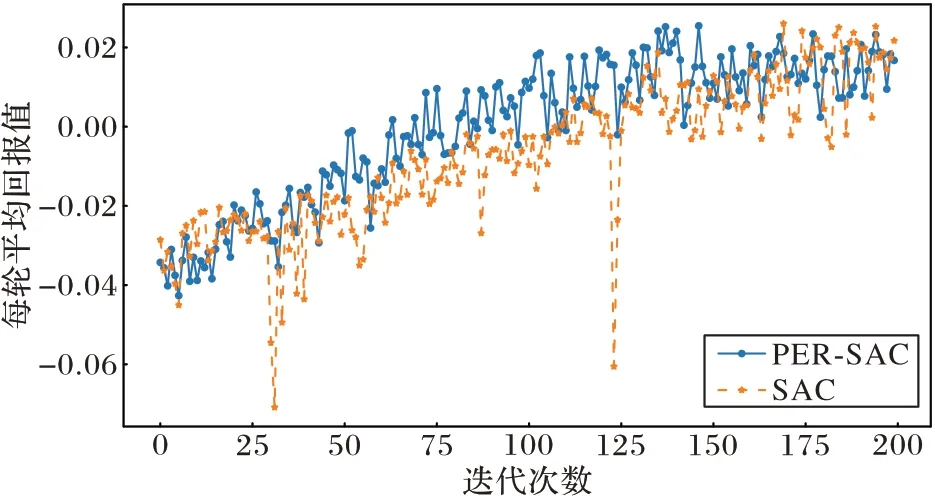
圖10 離散障礙環境下每輪的平均獎勵對比Fig.10 Comparison of average reward per round in discrete obstacle environment

PER-SAC 算法在30 輪后每一輪的平均回報值明顯比原始SAC 算法高，說明PER-SAC 算法每輪中機器人到達目標點的次數更多，并且在140 輪左右模型開始收斂。相較于原始SAC 算法，PER-SAC 算法收斂后每輪的平均回報值波動范圍小，更加穩定。

用兩種算法收斂后的模型進行路徑規劃，規劃結果如圖11 所示。PER-SAC 算法從起點到終點所用步數為248，原始SAC 算法為257。相較于原始SAC 算法，PER-SAC 算法能夠規劃出趨向目標點的相對更短路徑。

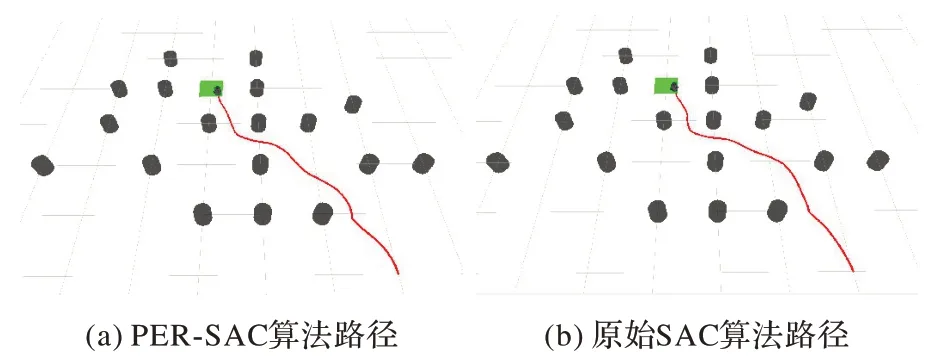
圖11 離散障礙環境下的路徑規劃Fig.11 Path planning in discrete obstacle environment

3.3 U型障礙物下的仿真

如離散障礙物下的訓練過程，同樣利用遷移學習將兩種算法在無障礙物環境下訓練好的模型遷移到5 m×5 m 的U型障礙物環境中作為初始化訓練模型。Gazebo 中U 型障礙物環境和移動機器人如圖12（a）所示，在Rviz 中如圖12（b）所示。起點為機器人初始位置，坐標為（-1.2，0），目標點坐標為（1.2，0）。

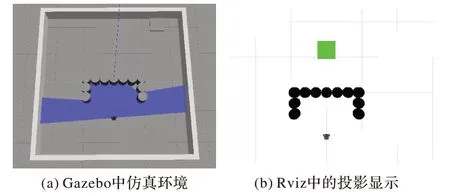
圖12 U型障礙物仿真環境Fig.12 U-shaped obstacle simulation environment

兩種算法各進行200 輪，每輪500 步的訓練后，同樣輸出平均回報值，如圖13 所示。

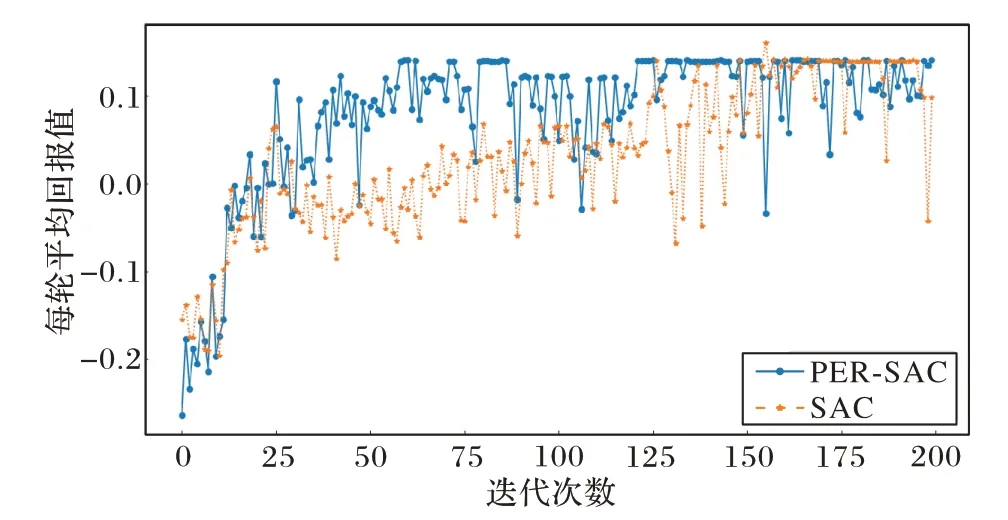
圖13 U型障礙環境下每輪的平均獎勵對比Fig.13 Comparison of average reward per round in U-shaped obstacle environment

PER-SAC 算法在25 輪后每一輪的平均獎勵明顯比原始SAC 算法高，說明每一輪機器人到達目標點的次數更多；PER-SAC 算法在140 輪左右收斂趨于穩定，而原始SAC 算法在180 輪左右，模型的訓練和收斂速度更快。

用兩種收斂后的模型進行路徑規劃，并且在Rviz 中繪制路徑，分別如圖14（a）和（b）所示。PER-SAC 算法從起點到終點所用步數為274，原始SAC 算法為298。相較于原始SAC 算法，PER-SAC 算法能更快走出障礙物，規劃出趨向目標點的相對較優路徑。

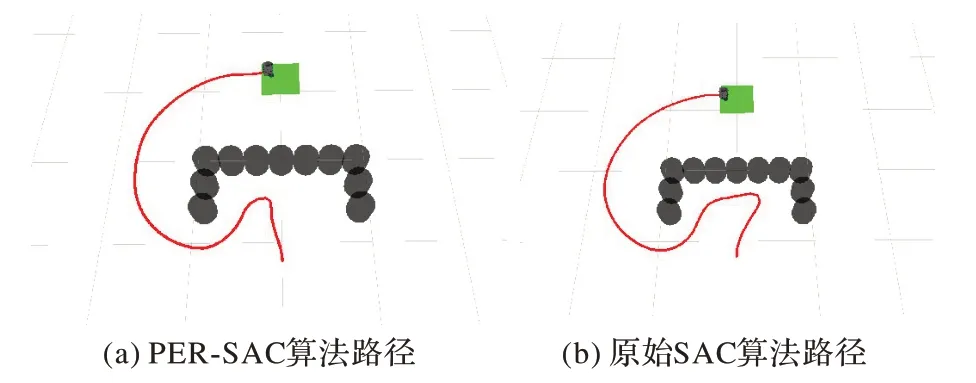
圖14 U型障礙環境下的路徑規劃Fig.14 Path planning in U-shaped obstacle environment

3.4 一型障礙物下的仿真

Gazebo 中一型障礙物環境和移動機器人如圖15（a）和（b）所示。起點為機器人初始位置，坐標為（-1.2，0），目標點坐標為（1.2，0）。

圖15 一型障礙物仿真環境Fig.15 1-shaped obstacle simulation environment

U 型障礙物是特殊的一型障礙物，使用3.3 節中U 型障礙物環境下訓練好的模型進行路徑規劃，檢測已經訓練好的算法的泛化性。如圖16 所示，在U 型障礙物環境下訓練好的算法同樣適用于一型障礙物環境，不需要重新訓練即可很好地完成路徑規劃任務。PER-SAC 算法從起點到終點所用步數為183，原始SAC 算法為226。PER-SAC 算法表現較好，在U 型環境中二者的模型就表現出選擇動作的差異，在一型障礙物中表現得更加明顯，機器人能更快繞出障礙區域。

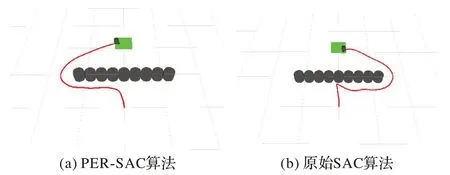
圖16 一型障礙環境下的路徑規劃Fig.16 Path planning in one-shaped obstacle environment

3.5 混合障礙物算法模型驗證

搭建兩個混合障礙物環境對算法進行驗證，混合障礙物是離散型、一型和U 型三種障礙物的組合。

混合障礙物環境一和移動機器人如圖17（a）和（b）所示。起點為機器人初始位置，坐標為（-2.2，-2.5），目標點為（1.8，1.3）。

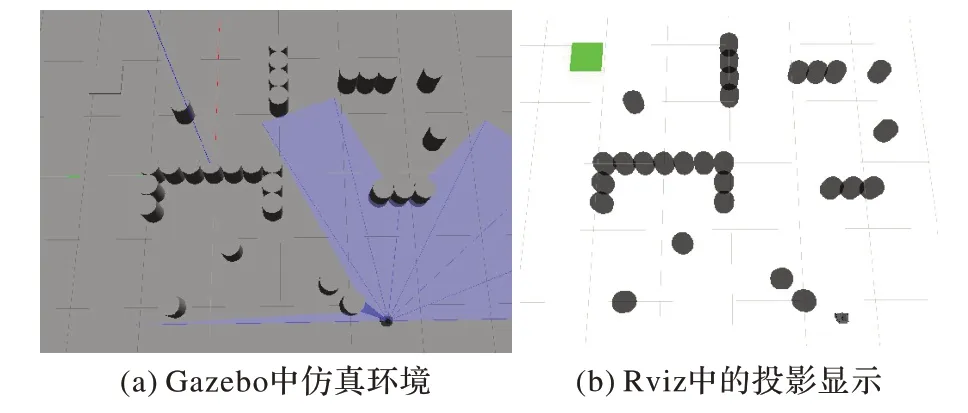
圖17 混合障礙環境一Fig.17 The first mixed obstacle environment

使用3.3 節中經過遷移學習從無障礙物到離散障礙物、再到U 型障礙物環境下訓練好的模型進行路徑規劃，如圖18所示，同樣不需要重新訓練即可很好地完成路徑規劃任務，并且PER-SAC 算法規劃的路徑較優。PER-SAC 算法從起點到終點所用步數為271，原始SAC 算法為304。

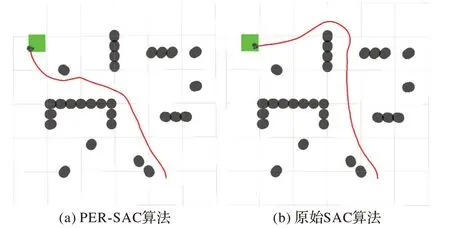
圖18 混合障礙環境一下的路徑規劃Fig.18 Path planning in the first mixed obstacle environment

混合障礙物環境二中，調整了障礙物和目標點的布局，使移動機器人更容易經過U 型障礙物，如圖19（a）和（b）所示。起點和目標點分別為（-2.2，-2.5）和（1.25，2）。

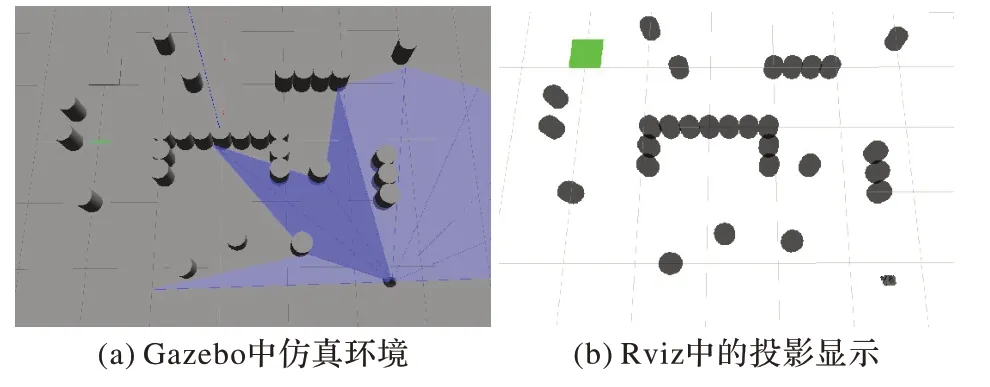
圖19 混合障礙物環境二Fig.19 The second mixed obstacle environment

路徑規劃結果如圖20（a）和（b）所示。PER-SAC 算法從起點到終點所用步數為279，原始SAC 算法為310。PER-SAC 算法規劃的路徑較優，能較好地規避障礙物。

圖20 混合障礙環境二下的路徑規劃Fig.20 Path planning in the second mixed obstacle environment

PER-SAC 算法經過遷移學習后訓練得到的模型，能夠在不同的環境中規劃一條從起點到目標點的路徑，算法具有一定的泛化能力，同時驗證了算法的有效性。

最后將兩種算法在上述三種仿真環境下的訓練時間進行匯總，如表2 所示。從表2 中可以看出，在每種環境下，所設計的PER-SAC 算法訓練或收斂時間更快。

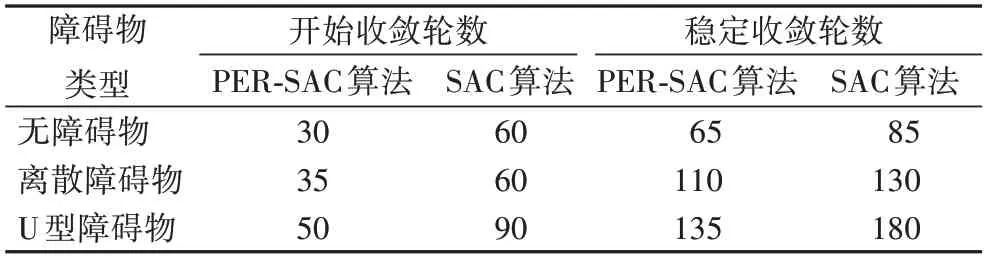
表2 算法收斂時間Tab.2 Algorithm convergence time

再對5 個仿真環境中路徑規劃時從起點到目標點的步數進行匯總，如表3 所示。從表3 中可以看出，在每種障礙物運行情況下，PER-SAC 算法均比原始SAC 算法所用步數少。

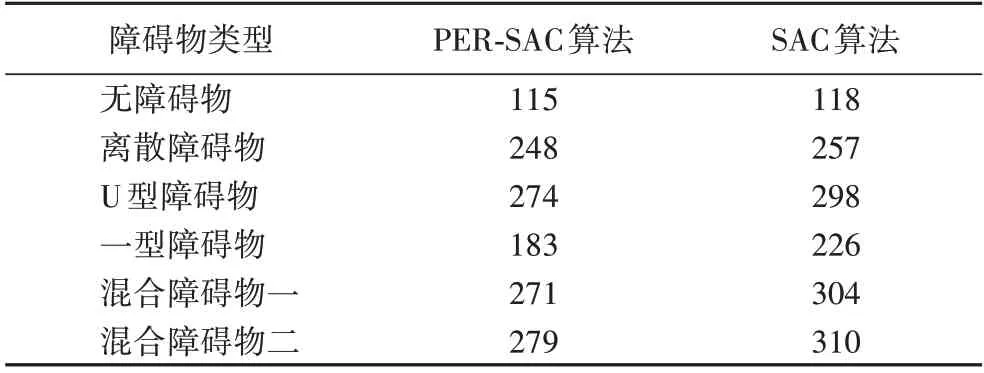
表3 到達目標所用步數Tab.3 Number of steps reaching target

4 結語

對于未知環境下的移動機器人局部路徑規劃問題，本文提出了一種基于SAC 和優先級經驗回放的PER-SAC 算法，并且在不同的仿真環境中與原始算法進行了對比實驗，驗證了新算法的有效性。PER-SAC 算法具有以下特點：

1）優先級經驗回放機制使經驗池中的每個樣本擁有了優先級，增加了重要程度較高的樣本被采樣的頻率，提高了訓練效率和穩定性。

2）在線運行時間和訓練時間沒有關聯，并且充分訓練后得到的收斂模型，實際運行時不需要再進行訓練。機器人通過傳感器實時感知當前環境信息，經訓練模型可以求出一條合理的局部規劃路徑，滿足運行的實時性需求。

3）利用參數遷移初始化不同障礙物環境下的模型參數，縮短訓練進程，加快模型收斂，模型的泛化性增加。

PER-SAC 算法目前還存在一些局限性，在計算網絡的損失函數時直接將重要性采樣權重與損失函數相乘，可能導致訓練的信息不夠充分。下一步的研究方向將考慮優化損失函數，進一步提升算法的性能，使機器人在更加復雜的環境下（多U 型、高混合型）實現局部路徑規劃任務。