Interface-induced topological phase and doping-modulated bandgap of two-dimensioanl graphene-like networks

Ningjing Yang(楊檸境), Hai Yang(楊海),?, and Guojun Jin(金國鈞),2,?

1School of Physics Science and Technology,Kunming University,Kunming 650214,China

2National Laboratory of Solid State Microstructures,Department of Physics,and Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China

Keywords: polyphenylene,interface,band structure,Zak phase,edge state

1. Introduction

Topological materials have maintained a hot topic in the last two decades. Common topological materials include topological insulators, topological superconductors, topological semimetals,topological metals,and magnetic topological insulator.[1–6]The general feature of topological materials is that they have topologically protected edge states, which are generated by non-trivial bulk bands. The earliest topological materials all have non-zero Berry curvature caused by spin–orbit coupling and are protected by time-reversal symmetry.[7]Integrating over the momentum space results in a topological invariant characterized by the Chern number.[8]Later on,new topological systems were discovered,which are protected by space inversion symmetry. In these topological systems,although the Berry curvature is zero, their topological edge states are protected by the non-zero vectored Zak phase.[9–13]The Zak phase refers to the integration of Berry connection,resulting in strongly non-trivial topological effects.[14,15]This kind of topological materials protected by space inversion symmetry regardless of spin–orbit coupling has attracted more and more attention.

Since it was prepared in 2004, graphene has started a research upsurge in carbon-based materials. At present, various carbon allotropes are being investigated in experimental measurements and theoretical calculations.[16–19]Among them, biphenylene is a newly prepared carbon monolayer,[20]which has been confirmed to be a topological material.[21]Moreover, biphenylene exhibits polarization, that is, its topological edge states appear in one direction and trivial behavior in the other. As is well known,for graphene carbon nanotubes and nanoribbons at finite scales, it has been predicted that they have a 3p-rule.[22,23]For their topological properties,both armchair nanoribbon junction states and nanotube systems have the topological rule related to their system size.[24–27]In addition, the 3prule is also exhibited in bilayer and twodimensional carbon materials.[28–31]The origin of this rule is inseparable from the nature of graphene itself and the additional restrictions. Researches on carbon-based materials emerge in an endless stream,including Dirac fermions,nodal rings, Weyl semimetals, etc., but most of them are demonstrated by numerical calculations, and there are lacking of physical analyses.[32,33]Moreover, many of the Dirac materials with topological properties are confirmed in the type-I,in contrast to other possible types.

In this paper, we theoretically study a series of network structures polymerized by polyphenyls, which has 3ptopological periodicity. It can be found that one third of them are topological material protected byC2space inversion symmetry and have a non-zero Zak phase. The topological rule is verified by first-principles calculations. Simultaneously, the topological phase has the Dirac point. Then, we obtain two kinds of topological phases in the band structures, one has gapless bulk dispersion and the other with gapped bulk dispersion. The gapped bulk dispersion with a non-trivial edge state is rare in space-inversion symmetric systems.[10,21,32,33]This topological property is caused by the periodic interface conditions. For a bulk gapless non-trivial phase,we construct a virtual potential in nanoribbon by doping B and N atoms,so as to open a gap in the bulk and make the system change from the gapless phase to the gapped phase.

2. Computational method

The electronic properties of the polyphenylene networks are calculated by the toolkit ATK’s first-principles method.[34,35]In the first-principles calculations, Perdew–Burke–Ernzerhof (PBE) functional is chosen under the generalized gradient approximation(GGA),the cut-off energy of 150 Ry and 10×10×1k-points grid are used. The lattice parameters and atomic positions are completely relaxed,and the convergence standards for energy and force are set to 10-5eV and 10-3eV/?A, respectively. The temperature is chosen at room temperature. We use a sufficiently large vacuum interval and add at least 15 ?A in the direction perpendicular to the electron transport plane to avoid interactions between layers.

3. Results and discussion

3.1. Structure and stability

We first characterize the structure of a polyphenylene network,as shown in Fig.1(a),and correspondingly the first Brillouin zone(BZ)shown in Fig.1(b).It can be seen that in a unit cell there are serial benzene rings connected by two quaternary rings at their periodic interface.Of course,the possible experimental preparation of these carbon allotropes is always important.In the recent experiments,net C and net Y,corresponding toN= 1 and 2, have been successfully prepared.[20,36]Especially for net C, which has been discussed as a topological material,[21]it has a topological phase with unidirectional charge polarization. Unlike the Chern topological insulators,it is protected by the space inversion symmetry. Topological adjustability in graphene nanoribbons and graphene nanotubes has recently attracted much attention,[24,25]especially for the armchair-type boundary conditions. Therefore, the unidirectional polarized topological properties similar to net C will appear for the systems withN ＞1 as well. For 2D monolayer materials,the structural stability is very important in the applications of practical electronic devices. Although biphenyl(net C)and net Y have been successfully prepared,we also need to find more graphene structures. We use the formation energy to evaluate their stability,defnied asEform=,whereEtotis the total energy of an allotrope,ECis the energy of a single carbon atom,andnCis the number of carbon atoms in the system. We calculate several sets of data and compare them with graphene,as shown in Fig.1(c). Moreover,the mechanical properties of allotropes are discussed(see the supplement material III).

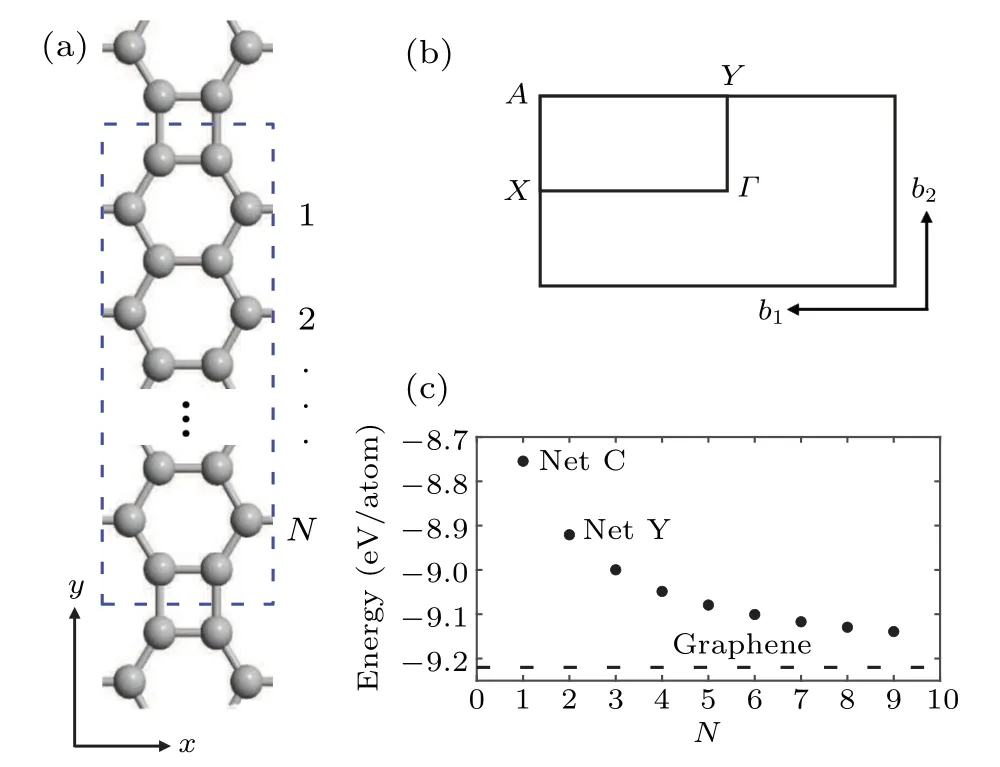
Fig.1. (a) Structural diagram of a polyphenylene network, forming a four-membered ring at the splicing. (b) The first Brillouin zone in the two-dimensional reciprocal space. (c)Formation energy of polyphenylene networks.

3.2. Origin of topological properties

Starting from a low-energy effective model, we investigate a polyphenylene network, which consists of finite polyphenyl molecules spliced together by four-membered rings at the longitudinal interface and is periodic in the transverse direction. By choosing the length and width of the quaternary rings to be equal,we can derive its wave function(for a detailed derivation,see supplement material I)

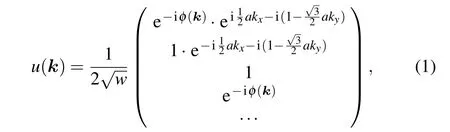
wherew=2N+1, which represents the number of rows of carbon atoms andais the lattice constant. The phase factor has the form

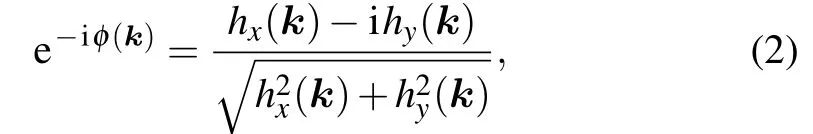
with

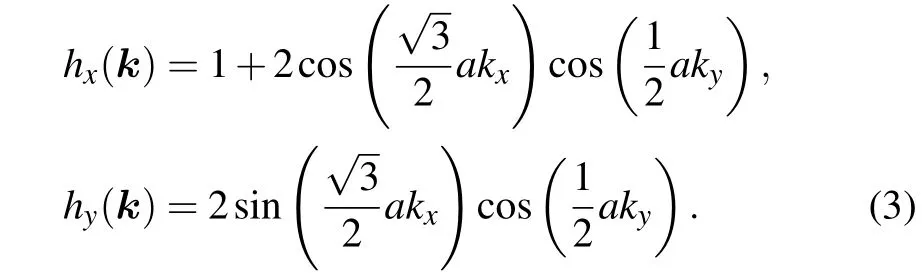
We definef(k)= e-iφ(k)as an eigenvalue of the parity operatorP,Pun(Γ)=fn(Γ)un(Γ). Taking the periodicity of the polyphenylene network in the vertical direction,kyneeds to be discretized,i.e.,

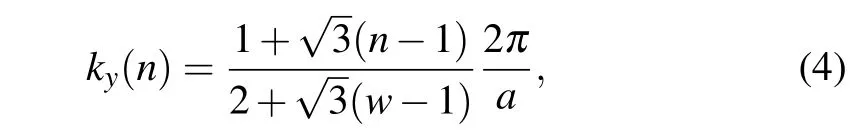
where the subband indexn=1,2,3,...,wrepresents all the occupied states. We discuss the importance of the interface condition in the supplement material II and confirm the robustness of this topological interface condition by means of density functional theory(DFT)calculations.

In fact, the topological property of this system is characterized by the non-zero Zak phase, which is defined as the integral of the Berry connection. The Berry connection of thenth band is defined asAn=〈unk|i?k|unk〉. When the Zak phase is non-zero, the system has charge polarization, resulting in topologically protected boundary states. The electric polarization is the quantization of the Zak phase,which is also the wave polarization given by the expression

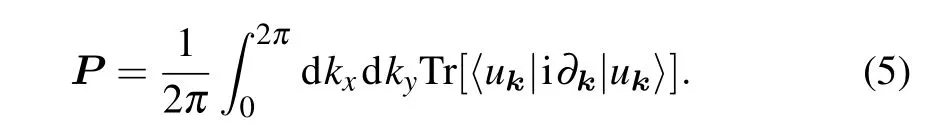
In a two-dimensional crystal system, the electric polarization can be viewed as a vectorP=(Pi,Pj),whose components depend on the direction of the wave vectorki(j). Since the polyphenylene network hasC2(πrotation along the out-ofplane direction)symmetry,hereki=kx,kj=ky,andPx/=Py.From the topological properties of biphenylene,it can be seen that the bulk–edge correspondence appears in the direction of the armchair boundary, while at the zigzag boundary, due to the intervention of the quaternary ring,the original bulk–edge correspondence in this direction is broken. That is to say,the charge is unidirectional polarized,and its electric polarization can be expressed as (0, 1/2). The space inversion symmetry has a strong constraint on the value ofP, which is independently determined by the parity of theΓpoint and theX(Y)point,[14]i.e.,

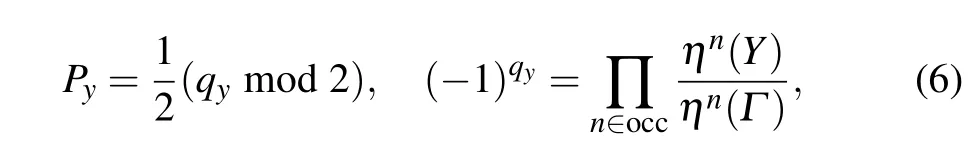
whereηrepresents parity,andqyis a topological invariant,0 or 1,so the value of the Zak phase depends on the electric polarization,which depends on the parity of the high symmetry point. From Eq.(6),we calculate thePyof the polyphenylene network,and its expression is

The above formula reveals the topological rule of theyaxis electric polarization of the polyphenylene network with a period of 3: if the number of benzene rings takes the remainder of 3 to be 1, we getPy=1/2, which is the topological phase. On the other hand,the remainder is 0 or 2,Py=0,and the system is a trivial phase. That is to say, the polyphenylene network can be further divided into topological phase and trivial phase according to the electric polarization parameters.

3.3. DFT calculation results

According to the above theoretical analyses, we calculate the band structures of polyphenylene networks at different cell-sizes. It is found that the electronic properties of these structures have a 3prepetition rule. When the remainder ofNto 3 is 1, the Dirac points appear near the Fermi level of the two-dimensional carbon allotropes, and along the high symmetry line ofΓ–Y, as shown in Figs. 2(a)–2(c). For other sizes,the valence or conduction bands of the two-dimensional carbon allotropes cross the Fermi level,so they are all metallic states(see the supplement material IV).All the DFT calculation results are consistent with the results in Refs.[21,37]. It is interesting to note that the Dirac cone undergoes a transition from type-II to type-III and then to type-I as the unit cell size increases,shown by the enlarged views at the Dirac point in Figs. 2(j)–2(l). Actually, this property is derived from the square rings,which brings the anisotropy to the whole system.As the size increases, the proportion of the projected density states of the quaternary ring gradually decreases,as shown in Figs.2(d)–2(f).The trend of the bond angles of the central carbon atom shows that the anisotropy of the system reduces with the increase of the cell size,as shown in Figs.2(g)–2(i).Therefore,the Dirac cone shifts toward isotropy. In fact,the 3p-rule has also been found in other similar 2D materials.[30,31]It can be understood that the key element of this topological 3p-rule is the periodic interface condition.

In order to verify its real topological properties, for the topological phase with unidirectional polarization in theyaxis, there must be a bulk–edge correspondence in the onedimensional nanoribbon system. We calculate the dispersion relations of nanoribbons for the two topological phase systemsN=1 and 4,as shown in Figs.3(a)and 3(b). The Bloch wave functions at the two pointsD1andD2are shown in Figs.3(c)and 3(d). It can be seen that they are non-trivial edge states near the Fermi level. But one is bulk gapless and the other is bulk gapped, the latter band gapEgis about 125 meV.This gapped phase ofN= 4 is a very good result and discovery,because such a large band gap is rare for space inversion symmetry-protected topological systems,which are usually bulk gapless.[10,21,32,33,38,39]An ideal quantum Hall device is internally non-conductive, but when a topological phase is bulk gapless,the interior will conduct electrically,and will inevitably affect the quantized conductance. This is unfavorable for observation and applications. It is also the difference between this system and a Chern topological insulator, which can open the bulk band gap through the spin–orbit coupling,thereby realizing edge states for a gapped bulk. For topological materials protected by space inversion symmetry,it is difficult for edge states to appear with a gapped bulk dispersion.

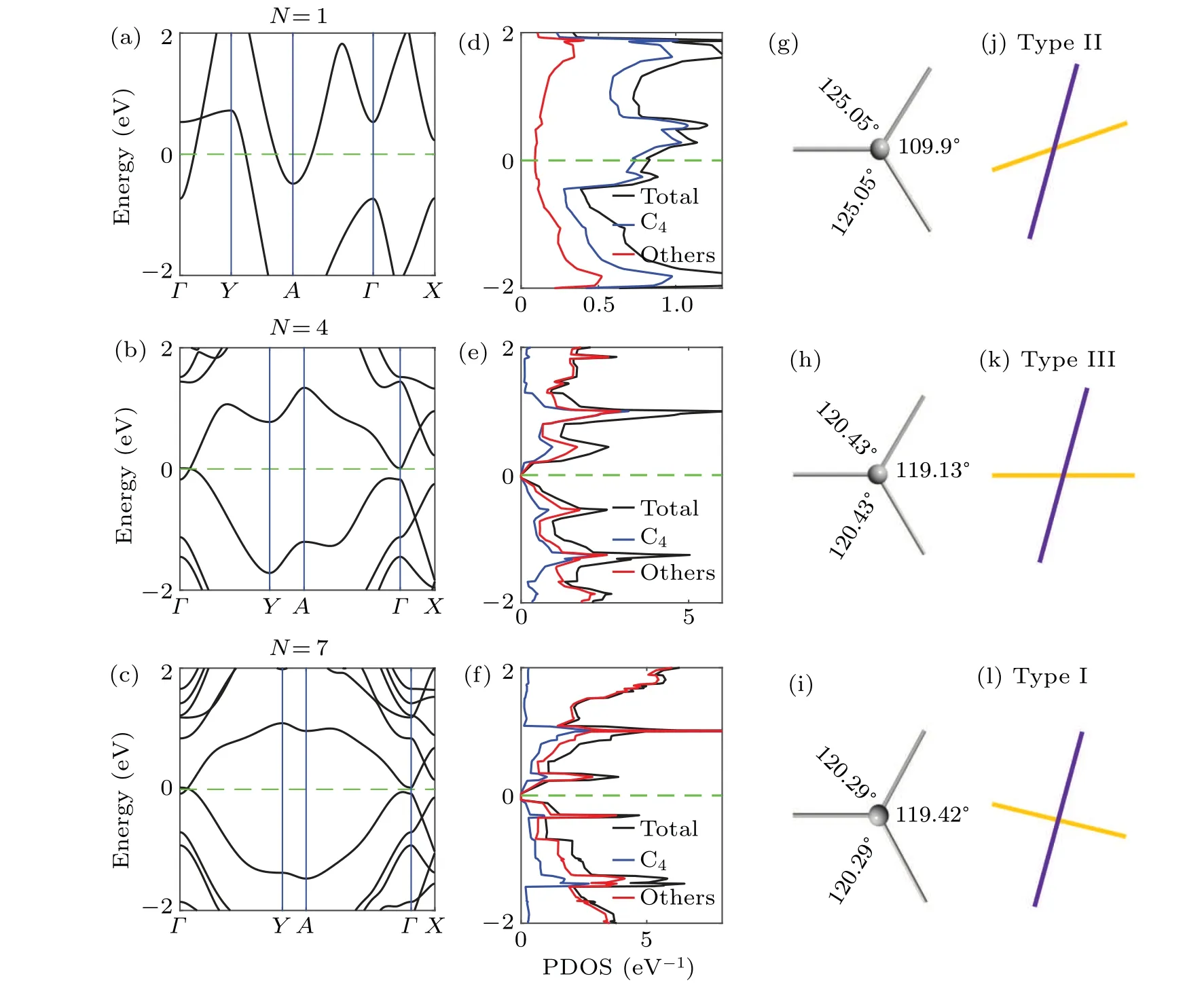
Fig.2. Band structures corresponding to N =1, 4, 7 polyphenylene networks are shown in (a), (b) and (c); (d), (e) and (f) correspond to the PDOSs of the left systems, where the blue lines represent the carbon atoms in the quaternary ring, the red lines represent the remaining six-membered ring carbon atoms, and the black lines represent the whole; (g), (h) and (i) correspond to the three bond angles of the carbon atoms at their central positions,respectively. The enlarged views of the Dirac points in the energy band structures are shown in(j),(k)and(l).

Fig.3. (a),(b)Dispersion relations of two nanoribbons for N=1 and N=4,respectively. Bulk(edge)states are indicated by solid black(red)lines. The gap between the upper and lower bands is labeled as Eg. (c),(d)The Bloch waves corresponding to D1 and D2 points,respectively.

3.4. Regulation of the build-in electric field

Although we obtain a very nice topological phase forN=4, it is still desirable to investigate the caseN=1, i.e.,a biphenylene nanoribbon as well. In favor of experimental observation,we consider to open the gapless bulk band by introducing a potential difference. For simplicity, we utilize a tight-binding model to perform the calculations for the dispersion relation. The Hamiltonian is

The first term is the transition term,andEiin the second term is the on-site energy. For this two-dimensional periodic system,we can see that the linearly intersecting bands are opened when an electric field is applied in theydirection with the strength of 0.2 V/?A, as shown in Fig. 4(a). But such a theoretical model is very difficult to realize in practice, so we can apply a virtual electric field by doping B and N atoms within the cell. This is easy to achieve experimentally.[40]At this time,Eiis expressed as the on-site-potential energy at the grid point position. With the help of the previous DFT calculation results,[41]we takeEB=3.34 eV,EN=-1.4 eV,tCN=2.6 eV,tCB=2.89 eV.At the same time,in order to well characterize the edge polarization scale of the wave function at each wave vector position,we refer to the inverse participation ratio(IPR),[42]which is defined as

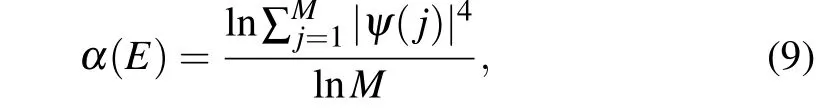
whereMis the total number of lattice points in the nanoribbon. Its value ranges from-1 to 0,and the more closer to 0,the more polarized wave function,as shown in Fig.4(c).When we only dope B and N atoms at the two ends of the biphenylene nanoribbon, we can open a small band gap, and the previously merged edge states are separated from each other, as shown in Fig.4(b). When the built-in electric field increases,we find that the bulk states are compressed, and the original dispersion relation of edge modes becomes a linear intersection, as shown in Fig.4(c). The wave-function moduli of the two selected points are shown in Fig. 4(d), which are indeed polarized at the boundaries. Besides,we reproduce the results very well by first-principles calculations for doping, see supplement material V.

From the response of the biphenylene nanoribbon to the built-in electric field,we can see that the voltage strength has a powerful and effective effect on the system. We then return to a more systematic discussion about the 2D graphene nanoribbon withN=4. We integrate over a unit cell to obtain the potential by accumulating the built-in electric field,guaranteed not to be canceled. It is worth noting that here each unit cell of the nanoribbon is doped, which is different from the form of constructing an electric field at both ends of a nanoribbon. We can move the position of the B atoms to adjust the distribution and magnitude of the built-in electric field,and obtain their band structures shown Figs.5(a)and 5(b). As the field is changed, the concurrence of the dispersion curves of the two edge modes decreases and becomes linear at the intersection. Under the built-in electric field,the original space inversion symmetry is broken,and the intrinsic topological polarization property will not be protected. The built-in electric field caused by doping modifies the original bulk polarization.From this, we can make the edge localized states disappear or degenerate by setting the form of the built-in electric field,as shown in Fig. 5(c). With intrinsic polarization, the edge modes of the nanoribbon will be regulated by the built-in electric field. For the discussion of the built-in electric field, rich energy spectrum and polarization properties are exhibited. A more detailed discussion will be provided in supplement material V.

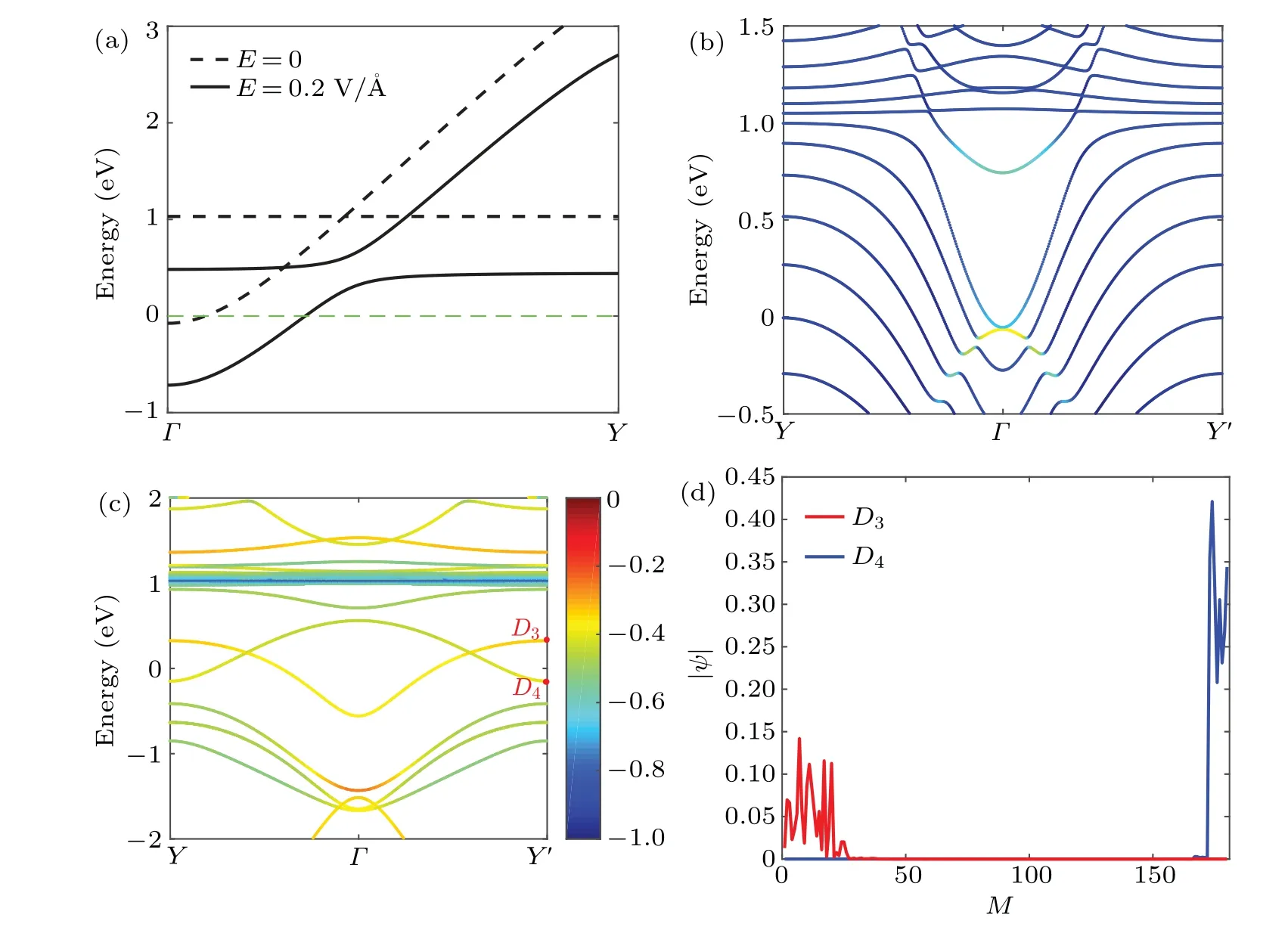
Fig.4. (a)The band structures of the biphenyl network under transverse electric fields of 0 and 0.2 V/?A. (b)The dispersion relation of doping B and N atoms at both ends of the nanoribbon. (c)Band structure at high doping rate. (d)Wave-function moduli corresponding to D3 and D4 in panel(c).

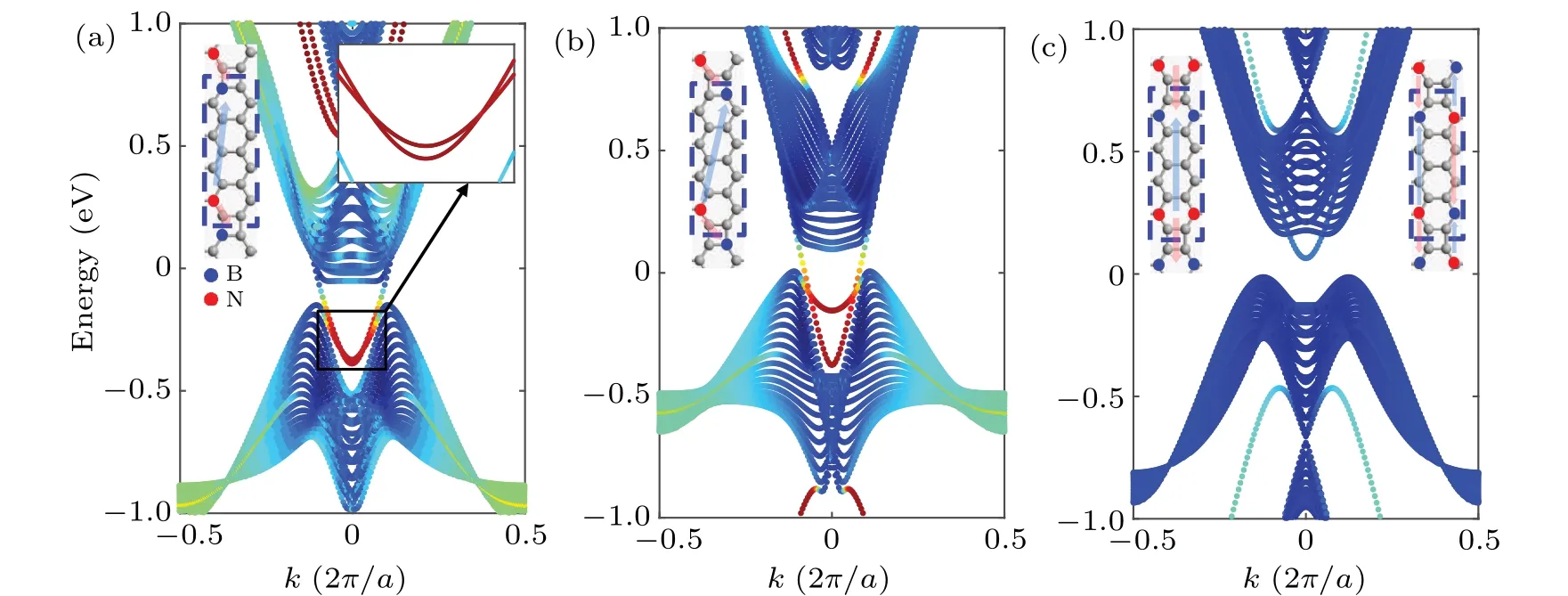
Fig.5. (a),(b)Band structures under two different built-in electric fields,where the doping positions of B and N atoms are shown in the upper left corners. (c)Band structure with the total potential of per unit cell being zero.

4. Conclusions

In summary,through the theoretical researches above,we have constructed a series of two-dimensional materials in the form of polyphenylene networks. The 3prule for these topological polyphenylene networks has been found: when the remainder of 3 for the number of benzene rings in each unit cell is 1, the system is a topological phase protected byC2space symmetry, accompanied by the Dirac point. The reliability and robustness of the 3prule have been verified by firstprinciples calculations. For the bulk–edge correspondence of the quasi one-dimensional nanoribbons of the topological 2D graphenes,we have further analyzed the two kinds of topological edge states. Meanwhile,through the tight-binding model,we have predicted that the bulk bandgap can be opened by doping B and N atoms, which is also verified by first-principles calculations. By adjusting the strength of the built-in electric field, the dispersion relations of the boundary modes become linearly intersecting Dirac shape. Our results suggest a strategy for searching carbon allotropes with topological properties, and an efficient approach for the experimental modulation and observation of space-inversion symmetry-induced edge states.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.12074156 and 12164023)and the Yunnan Local College Applied Basic Research Projects(Grant No.2021Y710).