例析高中數學與“圓”有關的最值問題

傅樹兵

(福建省漳州招商局經濟技術開發區海濱學校 363122)

與“圓”有關的最值問題解題思路靈活多變，其中函數視角、圖形視角、對稱視角、坐標視角、向量視角是解題的常用視角.不同視角適合分析的問題類型不同，解題細節存在較大差別，為使學生掌握不同解題視角的關鍵，教師應以經典例題為載體展開教學活動.

1 基于函數視角解題

基于對函數單調性的認識與理解不難發現，運用函數單調性解題時關鍵需把握兩點：(1)構建正確的函數類型；(2)以函數為依托探討最值問題需圍繞自變量開展.能否正確地確定自變量范圍，關系著求解結果的正確性，需根據習題情境以及實際情況，因此，應認真確定自變量的上限與下限.

例1 已知圓M和N的方程分別為：(x-cosθ)2+(y-sinθ)2=1(0≤θ<2π)，x2+y2-2x-4y=0.若兩圓交于A，B兩點，則tan∠ANB的最大值為____.

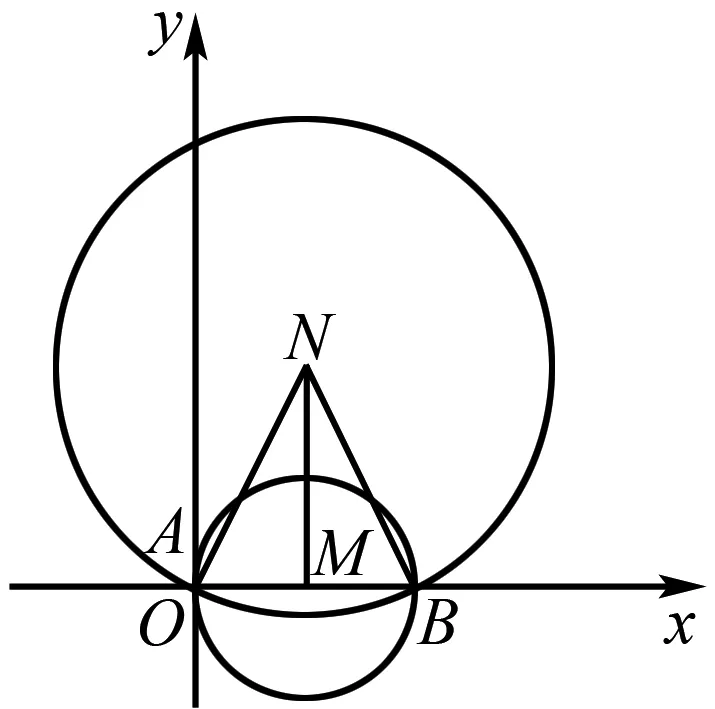
圖1

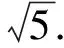
2 基于圖形視角解題

例2 已知直線x+y=4上存在一動點P.過點P向圓O：x2+y2=4引兩條切線，切點分別為A，B.在圓G：(x-4)2+(y-5)2=1上存在一動點M，則M到直線AB距離的最大值為____.

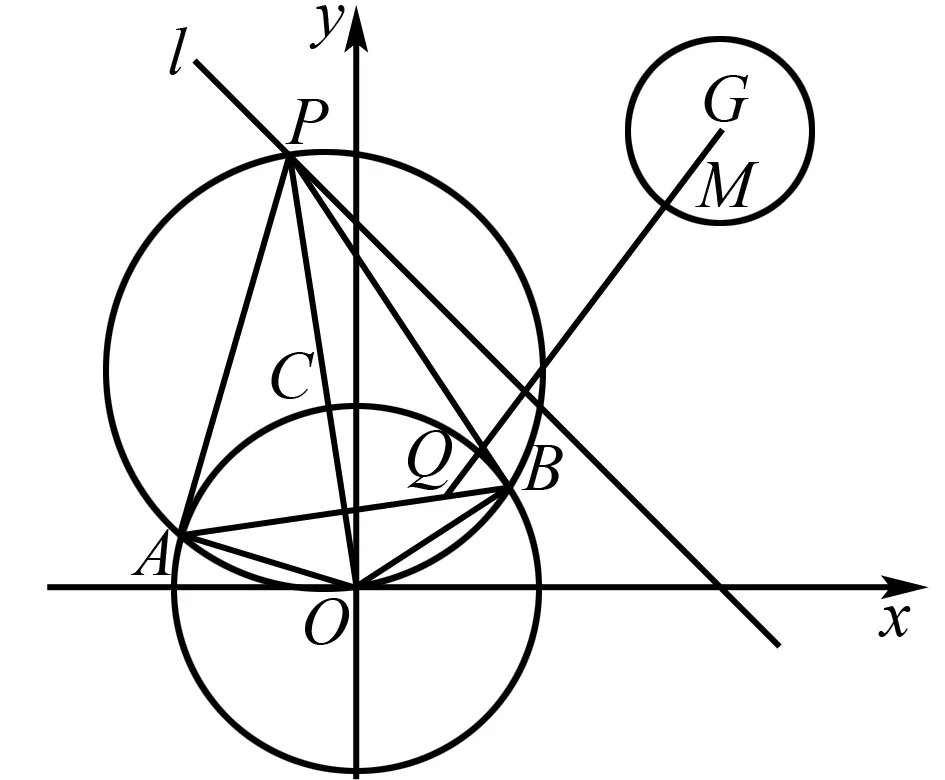
圖2

3 基于對稱視角解題

基于對稱視角解答與“圓”有關的最值問題，首先應突破如何尋找對稱關系這一重點.尋找對稱關系基于相關經驗以及對圖形關系的深入洞察，尤其需思考找到“對稱”對象后接下來該怎么處理，是否實現了化難為易的目的.根據經驗，經過“對稱”處理后，最值點往往出現在點的共線上，并且這一共線關系和一些圓的圓心關系密切.在這一方向指引下不難尋找到正確思路，接下來只需認真計算即可.

圖3

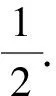
4 基于坐標視角解題

對于與“圓”有關最值問題的求解，可根據實際情況從坐標視角進行分析，通過坐標計算與圖形關系的結合不難尋找到解題思路.眾所周知，平面圖形中點的坐標與平面直角坐標系位置密切相關.為降低計算復雜度應首先依托現有的圖形、線段關系構建平面直角坐標系.在此基礎上合理設出相關參數，對相關點的位置加以準確刻畫.根據經驗一些點的位置往往是動態變化的，其軌跡會形成一個圓或圓的一段弧.對于圓弧而言可借助圓的方程以及對應參數范圍加以限定.以此為基礎充分利用題干中的已知條件逐漸向要求解的問題靠攏，直到經過運算能夠運用熟悉的知識順利得出結果.

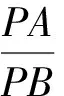
圖4

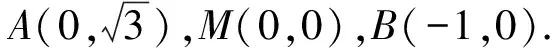
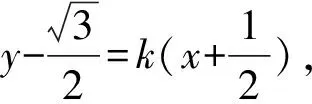
新課改思想對于教育教學有重要的指導作用，其要求的尊重學生學習成長階段，循序漸進的指導學生學習的觀點對于學生閱讀能力的培養也有指導作用。在探索數學閱讀之道的過程中，不能忽視新課改思想的應用，也不能忽視學生的身心發展階段性，要循序漸進的指導學生閱讀行為，培養學生閱讀習慣。

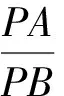
5 基于向量視角解題

向量與線段的區別在于向量具有方向性，使得其運算必須遵循自身的法則，但是向量的模與線段的長度是統一的.針對這一情況，可從向量視角解決一些與“圓”有關的最值問題.一般情況下，基于向量視角解決與“圓”有關的最值問題時，一般題干中都會有提示，如以向量的形式給出已知條件或者要求與向量相關的最值等.當然僅僅知道這一點是不行的，需充分運用已知條件通過抽象、運算、整理等處理，使得一些隱含的關系清晰地展示出來，為向量知識的運用做好鋪墊.

綜上所述，高中數學與“圓”有關的最值問題是非常重要的一類問題.該類問題又被進一步細分為多種情境，而且不同情境應用的解題思路有時存在較大差別.實踐中為使學生能夠舉一反三，實現解題能力以及解題靈活性的提升，在做好相關情境類似問題的基礎上講解常用的解題視角，并依托習題做好各視角在解題中的應用展示，鼓勵學生多思考、多揣摩，將相關細節理解到位，把控到位.