巧用六大模型 輕松解決四面體外接球問題

黃偉亮

(廣東省佛山市南海區石門中學 528248)

幾何體外接球問題是高中數學的一個難點，對學生空間想象能力有較高的要求，能很好地考查學生的數學素養，因此成為了高中階段各類考試的高頻考點.幾何體外接球的球心必在經過幾何體任意一個平面的外心且與該平面垂直的垂線上，兩個平面的外心的垂線相交于一點，該點就是幾何體的球心.四面體是空間中最基本的幾何體，且四面體一定有外接球.本文介紹解決四面體外接球問題的六大模型，利用這六大模型，能大大降低四面體外接球問題的難度，從而能輕松解決四面體外接球問題.

1 正方體模型

常見的能夠轉化為正方體模型的有3種四面體，特征如下：

圖1 圖2 圖3

(1)墻角三棱錐——三條兩兩互相垂直的線段(線段長度相等)，如圖1；

(2)鱉臑——三條兩兩互相垂直的線段(線段長度相等)，如圖2；

(3)正四面體，如圖3.

例1 (2019年全國新課標Ⅰ卷)如圖4，已知三棱錐P-ABC的四個頂點在球O的球面上，PA=PB=PC，△ABC是邊長為2的正三角形，E，F分別是PA，AB的中點，∠CEF=90°，則球O的體積為( ).

解法1不妨設側棱長為2a，則EF=a.

CE2=CF2-EF2=3-a2.

圖4

從而PA，PB，PC兩兩垂直.

解法2 三棱錐P-ABC為正三棱錐，因為正三棱錐的對棱互相垂直，所以PB⊥AC.

因為EF⊥CE，EF∥PB，

所以PB⊥CE.

又AC∩CE=C，所以PB⊥平面PAC.

解析如圖5，取AC中點M，連接SM，BM，因為AB=BC，SA=SC，所以SM⊥AC，BM⊥AC.

圖5

所以∠SMB就是二面角S-AC-B的平面角.

設S在底面ABC上的射影為S1，則S1在BM的延長線上，且S1M=SMcos(π-∠SMB)=1，于是四邊形ABCS1是正方形.

2 長方體模型

常見的能夠轉化為長方體模型的有3種四面體，特征如下：

圖6 圖7 圖8

(1)墻角三棱錐——三條兩兩互相垂直的線段(線段長度不完全相等)，如圖6；

(2)鱉臑——三條兩兩互相垂直的線段(線段長度不完全相等)，如圖7；

(3)對棱相等，如圖8.

評注正方體模型是長方形模型的特殊情況，圖1-圖3分別是圖6-圖8的特殊情況.

解析該三棱錐對棱相等，可轉化為長方體模型.設長方體的長寬高分別為a，b，c，則a2+b2=20，a2+c2=20，b2+c2=8.

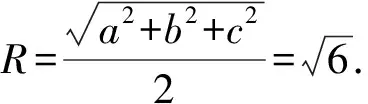
于是球心到平面ABC的距離為

例4(2022年衡水金卷一模)如圖9，兩個腰長均為10cm的等腰直角三角形拼成一個四邊形ABCD，現將四邊形ABCD沿BD折成直二面角A-BD-C，則三棱錐A-BCD的外接球的體積為____cm3.

圖9

3 圓柱模型

常見的能夠轉化為圓柱模型的四面體特征為：有一條棱垂直于一個平面，如圖10.

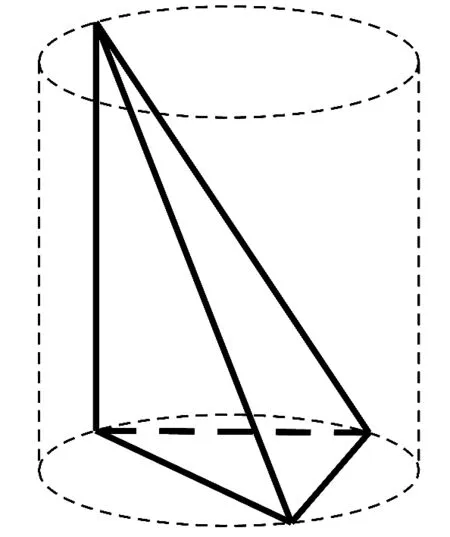
圖10

評注長方形模型是圓柱模型的特殊情況，圖3和圖6是圖10的特殊情況.

例5(2019年汕頭一模)三棱錐P-ABC中，PA⊥平面ABC，∠ABC=30°，△APC的面積為2，則三棱錐P-ABC的外接球體積的最小值為____.

于是△ABC的外接圓半徑r=x.

4 圓錐模型

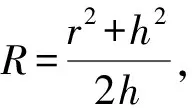
常見的能夠轉化為圓錐模型的四面體特征為：一個頂點在平面α(設另外三個點所在的平面為α)上的射影是這三個點的外接圓圓心，如圖11.

圖11

評注該四面體的特征也可以是3條棱相等.

解析由PA=PB=PC=4可知點P在平面ABC上的射影就是△ABC的外心，所以四面體P-ABC可轉化為圓錐模型.

5 二面角模型

證明如圖12，設△ABC和△BCD的外接圓圓心分別為O1和O2，過點O1和O2分別作平面ABC和平面BCD的垂線，兩垂線交于點O，則點O就是四面體A-BCD的外接球球心.

圖12

BC中點為M，O，O1，M，O2四點共圓，其外接圓直徑就是MO.

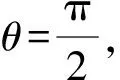
由于一般的二面角模型公式比較難記，建議按照以下步驟進行計算：

第1步：計算公共棱長度l；

例7(2015年江西高考)在矩形ABCD中，AB=4，BC=3，沿AC將矩形ABCD折成一個直二面角B-AC-D，則四面體ABCD的外接球的體積為( ).

例8 三棱錐P-ABC中，平面PAC⊥底面ABC，AB⊥AC，AB=BC=2，PA=PC=3，則三棱錐P-ABC外接球的表面積為____.

解析平面PAC⊥底面ABC，△ABC是直角三角形且直角是公共棱所對的角，所以三棱錐P-ABC外接球半徑等于△PAC的外接圓半徑.

6 建系模型

選擇適當的空間直角坐標系，設球心坐標為O(x,y,z)，外接球半徑為R，根據OA=OB=OC=OD=R，構建一個四元二次方程組，解出球心坐標以及球的半徑.一般地，只要我們建立適當的坐標系，使得球心的坐標未知數只有一個，同時使得某些點的坐標較容易寫，就能得到比較簡單的方程，從而能快速求出球心坐標及外接球半徑.

A.100π B.108π C.110π D.111π

圖13

所以外接球的表面積為111π.故選D.

根據四面體的不同特征，將四面體轉化為不同的模型，就能使用相應的模型公式迅速解決四面體外接球問題.六大模型部分內容是兼容互通的，同一個四面體，根據其特征的不同往往可以轉化為多種模型.如例1的2019年全國新課標Ⅰ卷的題目，由PA=PB=PC可將四面體轉化為圓錐模型.又如例9的2022年佛山一模的題目，由側面PAC⊥底面ABC，∠BAC=90°可知BA⊥平面PAC，由此可將四面體轉化為圓柱模型(以△ABC外接圓圓面為底面，PA為母線長的圓柱).總而言之，利用六大模型，能快速地解決四面體外接球問題，而對模型的甄別是解決四面體外接球問題的關鍵.