平面圖形翻折 解題思維展示
——一道立體幾何題的探究

劉金剛

(甘肅省禮縣第二中學 742201)

立體幾何是高中數學的主線之一，也是高考考查的主干內容之一．近年高考對立體幾何的考查，在直觀想象與創新意識等方面的要求較高，而平面圖形翻折成立體幾何的問題，就是其中一種比較吻合的考點．對于這類平面圖形的翻折問題，我們要化“動”為“靜”，“動”中取“靜”,“動”“靜”結合，找到點、直線、平面等相關要素之間變與不變的量，以及翻折過程中關鍵點的變化軌跡，合理切入，巧妙應用．

1 問題呈現

此題以一個直角三角形所對應的平面圖形為問題背景，結合線段上的動點與頂點所對應的直線進行翻折變化，構建相應的立體幾何圖形，利用另一線段中的存在點滿足線面垂直關系來合理創設，進而確定線段長度的變化情況，結合不等式恒成立引入參數，巧妙確定參數的最值問題，內涵豐富，知識交匯，形成一個“動”“靜”結合、“定值”“最值”鏈接的創新情境問題．

2 問題破解

解法1 (運動直觀法)由運動相對性，不妨固定△ABM，將△BCM繞BM翻折，作點C關于BM的對稱點C1，連接CC1，交BM點E，則點C在翻折時的軌跡為以E為圓心，CE為半徑的圓.

由題意CN⊥平面ABM，可知點C在底面ABM的投影點N在CC1上.

又點N在線段AB上，所以點N為線段CC1與AB的交點，當且僅當∠CBC1≥∠CBA時滿足題意.

如圖1所示，當點M從點C移動到點A的變化過程中，BN的長度由大變小，所以當點M與點A重合時，此時NBmin=1(因不含端點，故最小值1取不到).要使得NB>λ恒成立，則實數λ的最大值為1.

圖1

解后反思根據平面圖形翻折的變化規律，抓住“折痕”以及與“折痕”垂直的直線，借助輔助線的構建以及圖形的對稱性，可以巧妙直觀地確定相應翻折點的軌跡，以及直線與平面垂直條件下的投影情況．

設∠C′BN=φ，因為CN⊥平面ABM，所以∠C′BN為C′B與平面ABM所成的線面角.

則有NB=C′Bcosφ.

由三余弦定理，可得

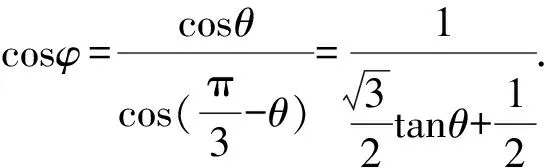
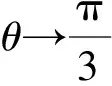
解后反思根據平面圖形的翻折變化，從角的視角入手，將線段長度轉化為角的三角函數，利用三余弦定理是點睛之筆與溝通橋梁，巧妙地將幾個對應的三角函數值聯系在一起，從而實現變形與轉化．

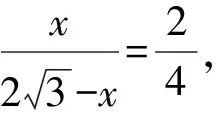
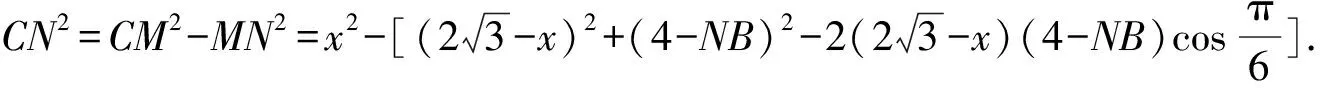
又CN2=CB2-NB2=4-NB2，

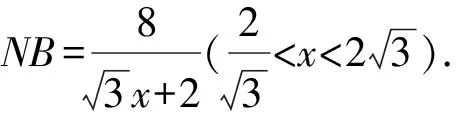
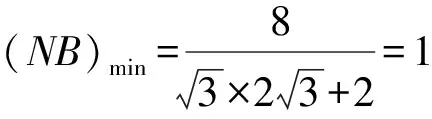
解后反思根據平面圖形的翻折過程，在不同平面內，引入線段長度的參數，利用解三角形思維，借助勾股定理與余弦定理的應用，巧妙表示對應線段長度的函數表達式，結合函數的單調性來確定對應的最值問題．

解法4 (四點向量定理法)如圖1所示，由CN⊥平面ABM，可得CN⊥BM.

設CM=x，結合四點向量定理，可得

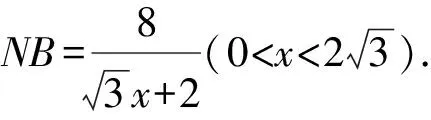
解后反思根據平面圖形翻折前后的變化規律確定平面上的四點，引入線段長度的參數，利用四點向量定理合理構建對應的平面向量關系式，通過垂直關系的確定，結合向量的模的轉化來構建對應的函數關系式，結合函數的單調性來確定對應的最值問題．

借助極端思維，易知要滿足CN⊥平面ABM，有兩個極限狀態:第一是BM為∠ABC的角平分線時，此時要滿足條件，趨近于BC與BA重合，可得NB→2；第二是點M與點A重合(或點C重合)時，此時NB→1；綜上分析可知NB∈(1，2)，要使得NB>λ恒成立，則實數λ的最大值為1.

解后反思根據平面圖形翻折過程中的動態變化規律，借助極端思維，從兩個極端狀態來特殊化分析，進而以“靜”促“動”，化“動”為“靜”，利用極端狀態下對應的線段長度來確定線段長度的取值情況，得以確定參數的最值問題．

3 變式拓展

平面圖形翻折過程中，涉及點、直線、平面等相關要素之間變與不變的量，可以從參數值情況、位置關系判斷、角度大小等多個不同視角加以變式與拓展．

A．存在某個位置，使得直線BD與直線AC垂直

B．存在某個位置，使得直線AB與直線CD垂直

C．存在某個位置，使得直線BC與直線AD垂直

D．對任意位置，三對直線“AC與BD”“CD與AB”“AD與BC”均不垂直

答案B．

4 教學啟示

4.1 抓住變化實質，挖掘運動軌跡

對于平面圖形翻折成立體幾何的問題，要分清翻折前后圖形的位置和數量關系的變與不變．一般地，位于“折痕”同側的點、線、面之間的位置和數量關系不變，而位于“折痕”兩側的則會發生變化．

而在變化過程中，需要抓住關鍵點的軌跡，所謂關鍵點是指翻折過程中變化的點，因為這些點的位置變化會帶動其他點、直線和平面的位置、數量關系的變化．只有分析清楚關鍵點的準確位置，才能確定其他點、線、面的關系，進而進行有關的推理、證明與計算等.

4.2 總結解題規律，全面提升能力

破解平面圖形翻折成立體幾何的問題，其關鍵是找準“動”與“靜”的相對關系，瞄準“變”與“不變”的確定關系，架起“平面”與“立體”的聯系橋梁，結合相關的知識加以推理與分析．在此過程中，借助空間的轉化，思維的跳躍，提升學生的數學能力，優化學生的思維品質，培養學生的數學核心素養．