品味提問藝術，優化解題教學

蘇州高新區第一初級中學校 王 珍

有效教學是當前教育教學領域中最為熱門的話題之一，更是一線數學教師十分關注的目標.眾所周知，教師若不諳熟提問的藝術，其教學就談不上有效，課堂教學的成功很大程度上取決于教師的巧妙提問及智慧點撥.由此可見，藝術性的提問對構建有效教學的作用不可低估.筆者在多年的教學實踐中十分注重提問的藝術性，也積累和總結出一定的經驗，下面就解題教學這一視角具體闡述.

1 凸顯層次性

在教學的過程中，我們偶爾會面臨這樣的情形：一個問題提出后，學生個個面面相覷，呈現無人應答的“冷場”局面.面對這樣的情形，一些教學經驗尚淺的教師則會埋怨學生不夠靈活，思維能力薄弱.事實上，造成這種“冷場”現象有時是因為教師設計的問題門檻過高.此時，需要教師針對問題的特征，設計一連串階梯性提問，層層遞進地引領學生的思維不斷延伸，循循善誘，助力學生更好地解決問題，提高學生的解題能力.

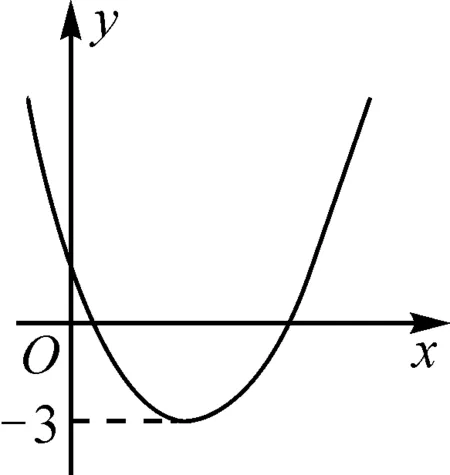
圖1

案例1圖1為二次函數y=ax2+bx+c(a≠0)的圖象，若關于x的方程|ax2+bx+c|=k(k≠0)有兩個不等實根，試求k的取值范圍.

由于學生初學二次函數，因而對此問題感覺到生疏且有難度.為了更好地促進學生理解，筆者精心設計如下問題串進行點撥：

問題1說一說y=ax2+bx+c的圖象是什么？

問題2y=|ax2+bx+c|的圖象呢？你能畫一畫嗎？

問題3那y=k的圖象呢？也請畫一畫.

問題4方程|ax2+bx+c|=k有兩個不等實根用圖象表示的意義是什么？

解題是檢驗學生知識掌握情況的有效標準.以上案例中，教師問題的拋出并非隨性而為，而是經過對具體學情的了解而精心設計的.正是由于有了各種思慮，教師才能針對原題巧妙點撥與誘導.這樣，通過一組拾階而上的問題引領學生思維不斷攀爬，逐步攀上一個嶄新的高度，從而使復雜問題迎刃而解，讓學生品嘗到解題成功的愉悅感，同時提高學生發現與挖掘的意識，讓學生掌握創新解題的一般方法[1].

2 體現探究性

初中數學教學效率低的癥結到底何在？筆者認為，從根本上來說就是不善變通的解題策略和鋪天蓋地的題海戰術.創新是民族進步的靈魂.因此，教師在設計數學問題時，需基于學生的“最近發展區”精心設計能體現探究性的數學問題，利用富有探究價值的習題促使學生都能竭盡所能地“跳一跳”，試著“摘桃子”.這樣深入探索的過程，不僅滿足了學生的求知欲望，還能給予學生解題的信心，這樣的問題才能達到“以一敵百”的效果.反之，教師若僅僅以解題的數量來論長短，教學效率低下的現狀根本無法得到改善，還會導致學生學習興趣的喪失，提高創新能力更是無從談起.這里需要重點關注的是，過難的問題會打消學生的積極性，過易的問題會影響學生的探索熱情，這就需要教師深鉆教材、了解學生，巧妙設計，方能提高學生的解題能力.

案例2以完全平方公式的拓展運用為例

此時的學生可以熟練運用公式進行多項式的運算，為了給學生提供更多的應用體驗來深化學生的認知，提升學生思維的靈活性，筆者精心設計了以下問題串：

問題1已知a+b=3，ab=2，求a2+b2，a-b.

問題2已知ab=3，試求a2+b2的最小值.

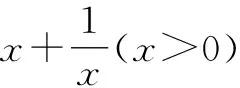
以上案例中，教師的問題設計是對教學內容的深度挖掘，關注到了問題的自然性，而并非人為創造的一些難題.通過這樣具有探究性的問題串，讓學生深刻明晰完全平方公式對于多項式運算的各種簡便，讓學生在靈活運用中學會思維、學會多角度去理解，更重要的是這里的活用也為后續“求代數式的最值”提供了方法上的借鑒.如此問題引領，讓整個課堂變得完美，讓學生真正進入思考與探索的境地，培養了學生的探究精神，真可謂效能豐富.

3 注重針對性

對于數學解題而言，教師設計的問題不僅需具有探究性，還需具有一定的針對性，才能讓學生在數學探究的過程中深入思考，多層次、多角度地探究，從而充分發揮問題的價值，讓學生通過解決問題全面而深刻地掌握知識，收獲真理，培養他們的創造性思維[2].

案例3以“四邊形問題中的折疊類問題”為例

問題1請試著通過折疊探尋矩形紙片的對稱中心，并找尋它的對稱軸.

問題2請利用剪刀剪一次，將矩形紙片分成面積相等的兩個部分.你能找到多少種不同的剪法？

問題3請從理論角度證明“過矩形對稱中心的直線平分矩形的面積”.

問題4上述理論除了以上角度，是否還能從圖形變化的角度予以證明？

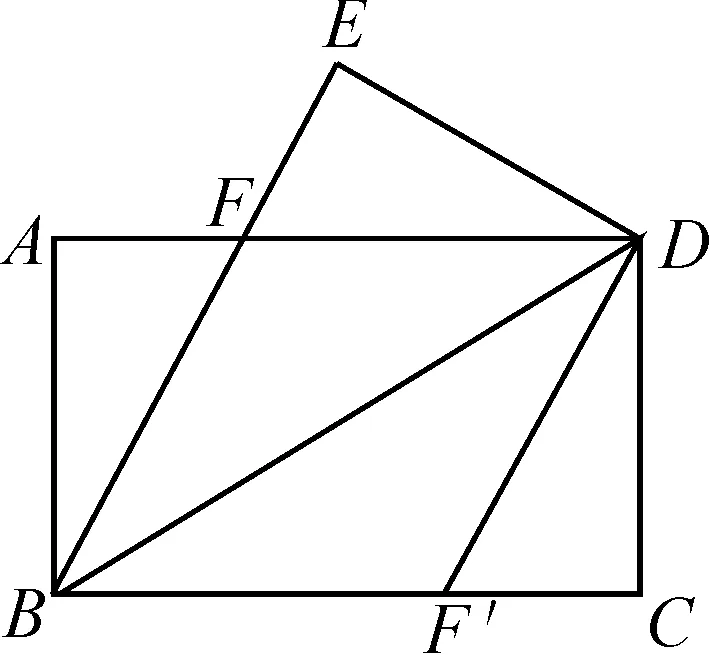
圖2

問題5如圖2，將矩形ABCD紙片沿著對角線BD折疊，將不重疊的部分剪掉，再展開重疊部分，將不重疊的兩個部分，即△ABF與△EDF拼成一個圖形，作圖并說一說拼出的圖形名稱.

問題6請試著從圖形變換的角度說明這些圖形是如何變換得到的.

問題7請試著將這些圖形進行分類.

問題8上述活動中，用到了什么數學思想方法？

問題9請試著用折紙法驗證“直角三角形斜邊上的中線等于斜邊的一半”.

問題10沿著BD剪開剛才的重合部分，得出△BDF.你是否能將這張紙片折疊成一個矩形？

不少教師在提問時只是微觀地考慮問題是否具有探究性，卻往往忽視了從宏觀上對知識本質的考量.以上案例中，教師設計的每一個問題都是經過了深思熟慮的.通過問題的解決不僅讓每個學生都能深化對四邊形的認識，而且培養了學生的創造性思維，建構了高效數學課堂，提高了學生的數學素養[3].

4 彰顯主體性

教學活動是一種雙邊活動，其中教師起到了主導作用，而作為教育客體的學生，也是教學的主體.如何在教學的過程中彰顯其主體地位呢？筆者認為，學生的主體性主要體現在積極動口、動手和動腦，在以動腦為核心的多感官參與下習得知識、生長能力、發展思維.課堂中可以引發學生多感官參與的一定是教師提出的體現教師創造性勞動成果的數學問題.因此，教師需設計彰顯主體性的數學問題，引起學生積極主動地思考，促使其在思考中辨析、在辨析中生成，讓學生的思維得到鍛煉與發展.

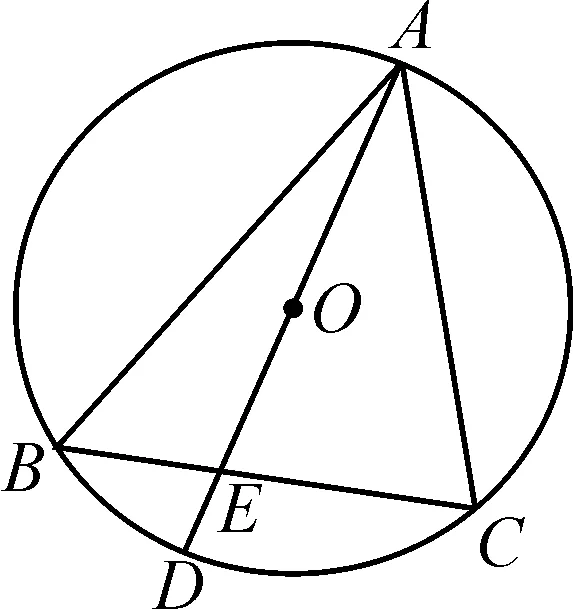
圖3

案例4如圖3，已知△ABC內接于⊙O，AD為⊙O的一條直徑，且與邊BC相交于點E.若OE=3，DE=2，試求tanC·tanB的值.

本題具有一定的難度.為了不造成學生無從下手的局面，筆者設計了以下問題串：

問題1試求BE∶CE的值.

問題2看到直徑，通常都會怎么作輔助線？

問題3tanB與tanC該如何轉化？

問題4你覺得tanC·tanB可以轉化為什么？

課堂中，有了教師的提問，才有了學生的深度思考；有了教師的提問，才有了學生的積極探索.以上案例中，教師以問題串為載體進行啟發與誘導，給予學生極大的思維支撐.更重要的是，在問題拋出后，教師充分留白，讓學生進行充分的思考、充分的討論和充分的表達，從而讓問題的解決水到渠成.如此提問，不僅彰顯了主體性，同時也較好地達成了教學目標，從而培養了學生的核心素養.

總之，在學生學習的道路上，教師充當的是引路人的角色，因此，教師需要深度鉆研、思考與反思提問的技巧與策略，讓學生通過精心設計的問題得到更好的訓練與展示，以達到優化教學的效果.對于解題教學而言，面對不同題目，教師需要針對具體的學情，針對性地精心設計，這樣才能發揮提問的作用，優化解題教學，培養學生的思維能力.