水利樞紐對水文水力特性的影響分析
郭健常
(大同泰瑞集團建設有限公司,山西 大同 037000)
1 概 述
水利樞紐是保障水利灌溉、畜牧養殖等生產生活的重要保障,通過在江、河合適的河段修建的壩、水電站等建筑,達到水利發電、蓄水引水、旅游養殖等目的。水利樞紐的興建關系到民生問題,直接或間接地影響著周邊居民的生產生活。但水利樞紐的修建同樣會在短期或長期內對當地的水文水力特性造成一定的影響,這種影響或利或弊,通過對其影響機理的研究,進而對水利樞紐以及當地水文情況進行有利調節,能夠造福民生;相反,則可能對當地生態及人民財產造成破壞[1-4]。因此,研究水利樞紐對當地水文特征的影響成為當務之急。
在此背景下,許多學者針對水利樞紐對上游或下游水文特征的影響情況進行了研究。劉金星[5]以東莊水利樞紐為例,通過三維的紊流雙方程模型對該水利樞紐的表孔寬尾墩的消洪性能進行了計算并進行試驗,發現計算得出的結果與試驗結果吻合度較高,該水利樞紐具備較好的消洪性能。龔麗[6]基于老龍口水利樞紐工程的豎縫與堰組合式魚道的水力性能,采用湍流模型對該水利樞紐的流速和紊動能進行了研究,發現該魚道內水流結構穩定,主流衰減較為明顯,具有一定的消洪效果。包中進[7]通過對蕭山水利樞紐進行研究,并采用物理模型及平面二維模型對其進水口引渠進行了分析論證,該樞紐原方案布置的引水渠存在較大范圍的回流。胡春明[8]研究了紅花爾基水利樞紐對下游伊敏河水文情勢的影響,并采用IHA及RVA法評估水文總體變化的程度,結果表明伊敏河降水徑流響應較為顯著,該水利樞紐整體上對伊敏河及下游流域形成較為積極的影響。柴軍瑞[9]基于黃河大柳樹壩區的松動巖體,采用統計學方法,確定了壩基巖體的參數分布,并對滲透系數張量進行了修正,驗證了壩區巖體滲透性較大。
本文以某地水利樞紐工程為例,借助該地水文實測資料,對該樞紐在蓄水前后的斷面變化進行了研究,揭示了水利樞紐對水文水力特性的演變規律,為類似水利樞紐及水文特性的調節提供一定參考依據。
2 工程概況
水利樞紐A位于某市河道下游4km處,主要由電站、沖沙閘、船閘、泄水閘、擋水壩5部分構成,具有蓄水、水運、泄洪等功能。該樞紐于上世紀50年代進行規劃,并于70年代開工,修建至今共抽水1 800×108m3,控制水域達100×104km2,壩區總庫容為15.1×108m3。電站擁有發電機組20臺,發電功率271.8×104kW,年發電量150×108kW·h。由于其施工條件較差,土石方挖填量巨大,總計達7×108m3,主體及附屬結構混凝土澆筑達1×108m3,鋼筋消耗量約為7.7×104t。樞紐包含3座船閘、27座沖沙閘與15座泄水閘,當閘體全部開啟時,其最大泄洪量約為10×104m3。其中,3個船閘均為單級船閘,1號、2號船閘長寬分別為270、30m;3號船閘長寬分別為120、15m;擋水壩長2 588m,壩體最高點達45m。
水利樞紐A在其整體水系規劃中主要起反調節作用,分別從航運與發電量兩個方面體現。在航運方面,枯水期時,由于下游水位不穩定,波動幅度較大,不利于船舶停泊與運輸,因此需要借助該水利樞紐進行反調節;在發電方面,水系主電站枯水期發電負荷較大,同樣需要借助該樞紐電站進行負荷分擔。
3 研究方法
對于水利樞紐A在豐水期蓄水前后的水位與流量關系,由于豐水期中水流具體表現為典型的漸變不恒定流動模式,因此本文采用反映非恒定漸變水流運動規律的偏微分方程組,即Saint Venant方程組,其連續方程為:
(1)
其運動方程為:
(2)
式中:Q為流量;x為水流路程;A為過水橫斷面積;t為水流時間;v為流速;y為水體深度;g為重力加速度(9.8N/kg);i0為水利樞紐底部坡度;C為謝才系數;R為水力半徑。
聯立式(1)、式(2),可得到Saint Venant動力方程:
(3)
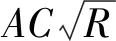
(4)
當水流方式為均勻流時,可將式(4)變為:
(5)
式中:Q0為水流方式,為均勻流中的流量。
4 結果分析
4.1 豐水期水位-流量變化分析
該水利樞紐在豐水期水庫中蓄水之后,其下游河道的水文水力特性發生改變。一旦下游河道的水文水力特性發生變化,該市水利樞紐A所在河段的水流作用力必然會隨之改變,并帶動水波類型的改變。本文通過當地實測水文資料,分別選取1974、1981、1987及2004共4個水流量達到6 000m3/s的年份進行分析比較,并將其歸類為蓄水前和蓄水后年份。其中,蓄水前年份為1974與1981年,蓄水后年份為1987與2004年,蓄水前后流量與水位的變化圖見圖1。
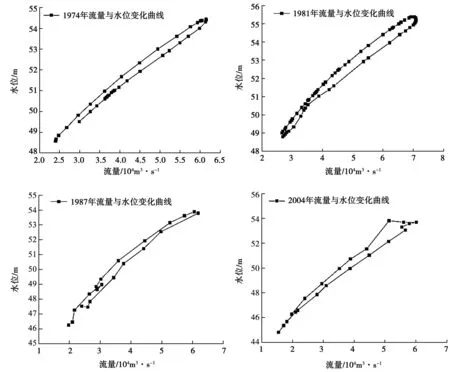
圖1 蓄水前后水位與流量變化圖
從蓄水前的1974與1981年的水位流量變化圖可以看出,蓄水前年份的水位與流量變化呈現出光滑的繩套狀,符合Saint Venant方程組中式(5)所描述的均勻流運動規律。究其原因在于該河段受人為因素較少,呈現出天然流態,上游水流經過該水利樞紐時,攜帶的能量會均勻分布于河道兩側,因此慣性項對其影響效果較小,可忽略不計,因此該種水波屬于擴散波類型,其水流的水力特性主要由阻力項和河底比降構成。在該水利樞紐蓄水完成后,即在1987和2004年后,水位流量曲線呈現出明顯的變化,由之前的光滑繩套狀演變為不規則形狀,之前天然的連續性水流模式被破壞,河道兩側的能量產生變化,在壩區前河道水流勢能增大,一部分轉化為電能,另一部分轉化為機械能繼續向前流動,導致水流在流過壩區后流速明顯增大,因此Saint Venant方程組中所描述的慣性項不能被忽略。但由于其整體趨勢仍大致表現為繩套狀,說明河底比降仍然存在,因此該種水波屬于動力波類型。
4.2 蓄水前后的斷面形狀分析
由于該河段在第四紀沖積后基本斷面已經定型,因此主要的形狀變化來源于人為活動。通過實測記錄資料,繪制蓄水前后形狀及高程變化,見圖2。

圖2 蓄水前后斷面形狀變化圖
圖2為蓄水前后通過高程于起點距所反映的蓄水前后斷面形狀變化圖。從圖2中可以看出,蓄水前斷面形狀整體上變化規律較為不明顯,形狀變化不大,但在蓄水后的年份如1985、1995年斷面變化較為顯著。
為了更進一步得出具體的水位變化趨勢,本文通過實測記錄數據,繪制蓄水前1975年與蓄水后1995年的水位隨斷面面積變化曲線,見圖3。
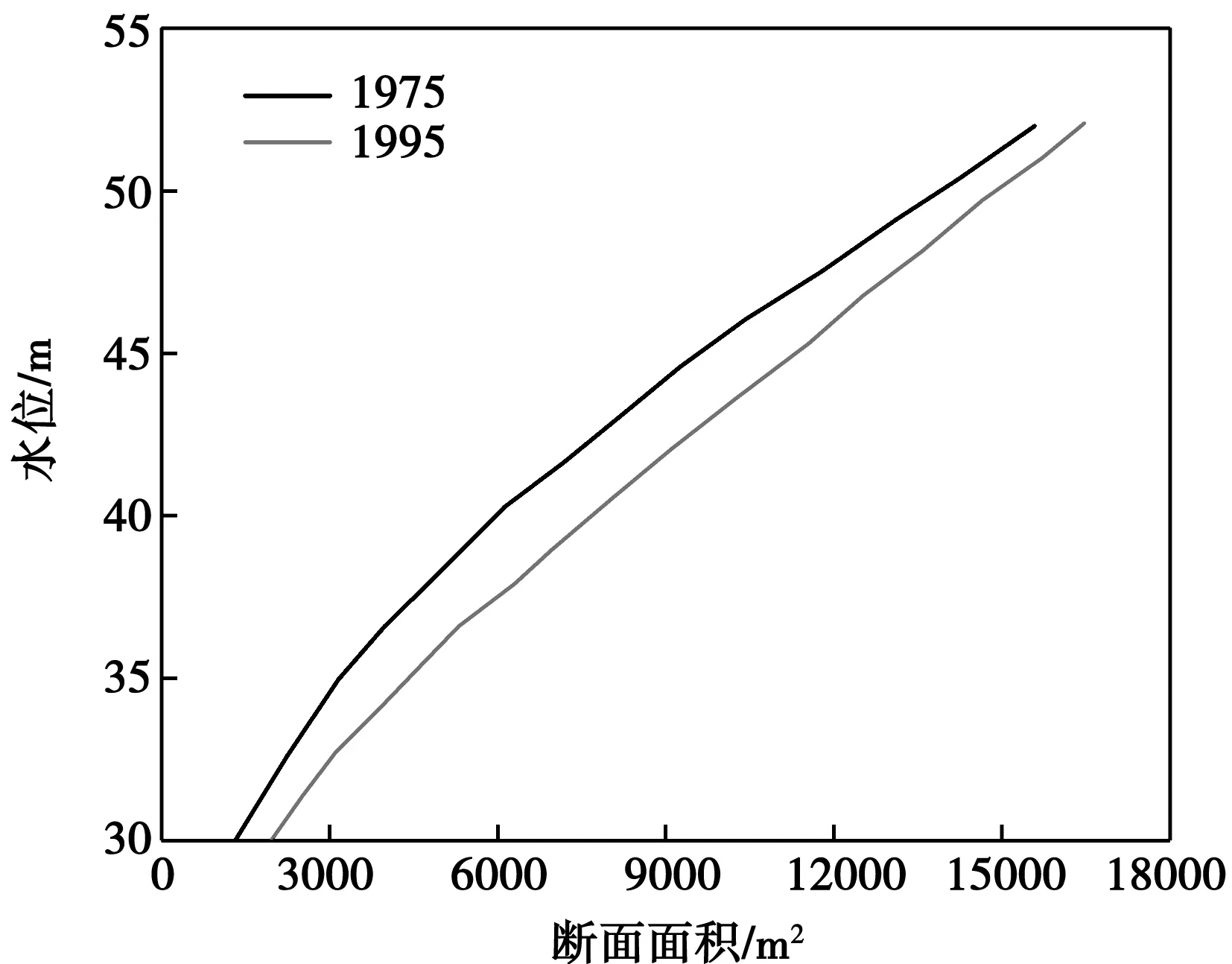
圖3 水位隨斷面面積變化曲線
從圖3中可以看出,隨著蓄水的完成,曲線會向右偏移,說明河床形狀發生了變化,在上游水流沖擊的作用下,同一水位條件下的斷面面積會變大。其原因是蓄水后水位會升高,壩區前的河段水流流速降低,導致水流挾沙能力下降,下游的輸沙量銳減,壩體的阻隔使得泥沙堆積導致斷面增大。同樣由于蓄水后,壩區后由于勢能轉化的機械能增加,流速增大使得壩區后的水流挾沙能力比天然狀態下增加,天然狀態下無法被帶走的泥沙會被帶走,使得河道變深,因此增加的水流流速改變了該段的斷面形狀。
4.3 蓄水前后的斷面水位分析
為了分析斷面形狀變化對水位及流量的變化規律,選取水流較為平緩的流量條件進行分析。由于5 000m3/s流量下水流平穩,受慣性力影響較小,因此本文通過1960年以來該地記錄的5 000m3/s流量下的水位變化數據繪制成圖4。
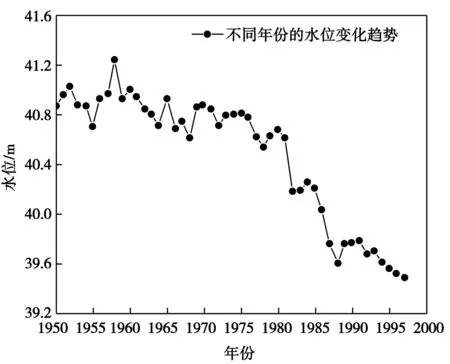
圖4 5 000m3/s流量下的不同年份水位變化圖
從圖4中可以看出,蓄水前的年份所在水位整體上處于較高狀態,雖然隨年份不同會產生一定波動,但總體上變化不大。在1981年蓄水之后,水位逐年呈現出降低的趨勢。該趨勢說明在水位相同的情況下,斷面面積增大,在水流流量一定的情況下水位會出現降低的情況。
為了對高水位下的水文特征進行分析,本文采用3次多項式曲線擬合的方法,對蓄水前后4個相似年份水位流量進行分析,并繪制成圖5。從圖5中可以看出,在水流流量較低的情況下,蓄水后水位會出現明顯的降低,隨著流量的逐漸增大,水位變化效果逐漸不明顯,在達到最大流量后,水位變化幾乎可以忽略不計。原因可能是低水位時,流量較小,整個流段較為平穩,因此水流攜帶的能量小,河床在沖擊下變深,導致在流量相同下水位會變低;在水位居中時,上游水流攜帶的能量較低水位時增多,水流通過壩體后慣性力增大,加之斷面形狀的改變使得水位下降幅度達到峰值;在高水位下,由于水頭高,勢能最大,使壩區前水位增加的能量占比降低。
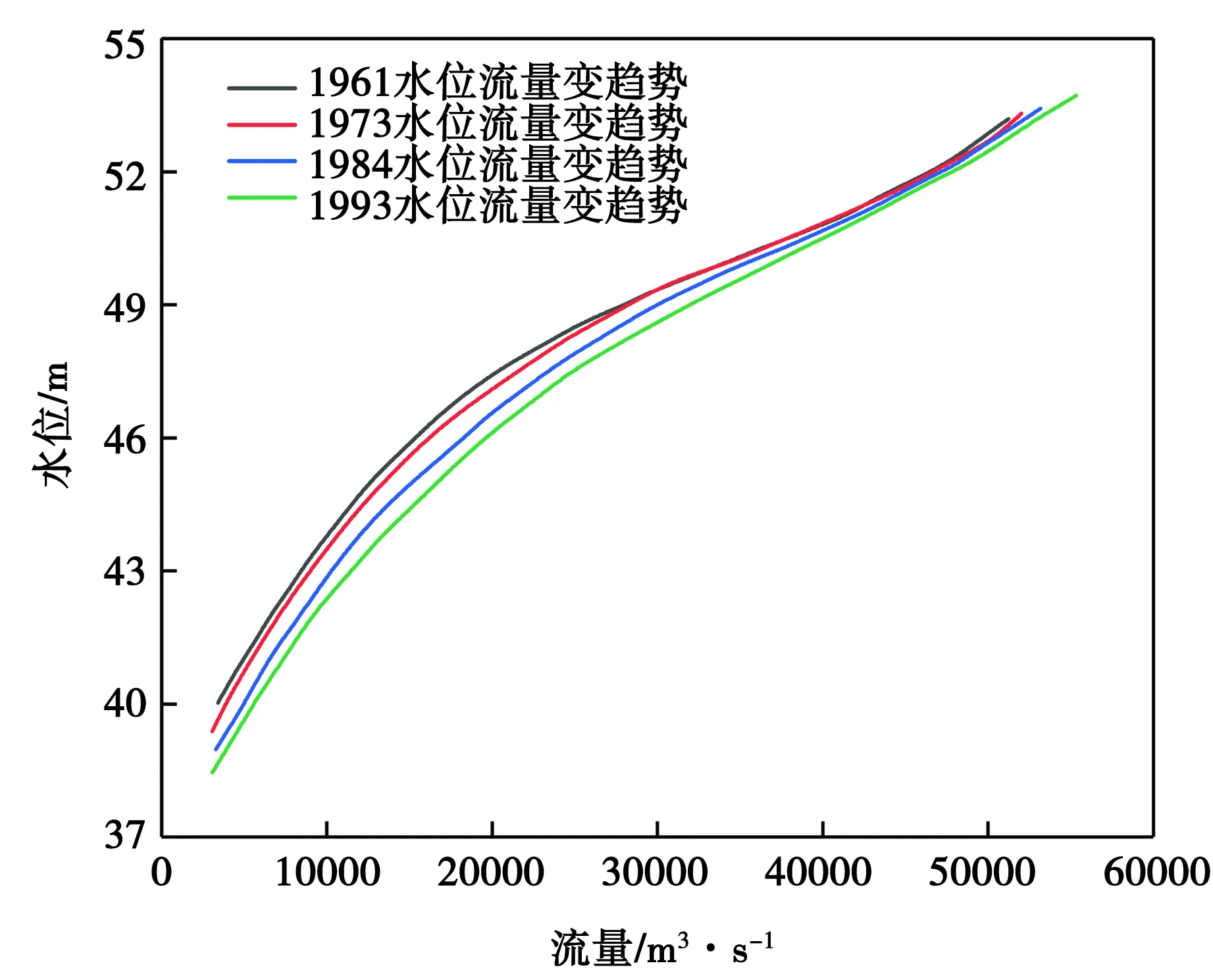
圖5 不同斷面下的水位隨流量變化趨勢
4 結 論
本文以某地水利樞紐A為研究對象,借助Saint Venant運動模型以及水利樞紐A多年蓄水前后的實測數據,通過對該水利樞紐蓄水前后的水位-流量、斷面面積變化,斷面面積變化下的水位特征進行研究分析,結論如下:
1)該水利樞紐的水波在蓄水前屬于擴散波形式,在蓄水后轉變為動力波形式。
2)該水利樞紐在蓄水前,壩區前水流流速較為平穩,水流流速較低,導致水流挾沙能力下降,下游輸沙量銳減,壩體的阻隔使泥沙堆積,導致斷面增大;蓄水后,壩區后由于勢能轉化的機械能增加,流速增大使壩區后的水流挾沙能力比天然狀態下增加,天然狀態下無法被帶走的泥沙會被帶走,使河床變深,進而改變該段斷面形狀。
3)在水流流量較低的情況下,蓄水后水位會出現明顯的降低,隨著流量的逐漸增大,水位變化效果逐漸不明顯,在達到最大流量后,水位變化幾乎可以忽略不計。

