基于內外回流污泥形態參數的水質預報

谷精華，劉 健，范文玉*，趙立杰，左 越，司文豪

(1.沈陽化工大學機械與動力工程學院，遼寧 沈陽 110142；2.沈陽化工大學環境與安全工程學院，遼寧 沈陽 110142；3.沈陽化工大學信息工程學院，遼寧 沈陽 110142)

1 材料與方法

1. 1 活性污泥及水樣采集

本試驗的活性污泥樣本采自沈陽某A2O工藝污水處理廠，為了保持試驗的一致性，每次均在固定點液面下50 cm處采集內、外回流活性污泥樣本。為了與內、外回流污泥建立直接的聯系，在采集活性污泥樣本的同時，也在好氧池出水口采集了瞬時水樣進行測定。每次活性污泥樣品和出水樣品均采集500 mL，為了減小微生物對水質的影響，樣品采集、圖像采集與水質指標測定之間的間隔時間不超過3 h。本試驗共進行6個月，共采集樣本91組。期間收集了污水處理廠的運行參數，具體見表1。

表1 試驗期間污水處理廠的運行參數

1. 2 水質指標及測定方法

由于所采集的水樣為泥水混合液，所以在測定前需要對其進行預處理，即首先將水樣過濾，取濾液調節其pH值至中性，然后將水樣稀釋至合適的待測范圍。水樣中BOD、COD、TN和TP的測定分別采用《水質 五日生化需氧量(BOD5)的測定 稀釋與接種法》(HJ 505—2009)中的稀釋接種法、《水質 化學需氧量的測定 重絡酸鹽法》(GB 11914—89)中的重鉻酸鉀法、《水質 總氮的測定 堿性過硫酸鉀消解紫外分光光度法》(GB 11894—89)中的過硫酸鉀紫外分光光度法和《水質 總磷的測定 鉬酸銨分光光度法》(GB 11893—89)中的鉬酸銨分光光度法。

1. 3 活性污泥絮體圖像處理與分析

1.3.1 圖像采集

為了保證較大活性污泥絮體的通過，首先使用帶有尖端截面槍頭的校準移液槍，取10 μL活性污泥樣品于載玻片上[14]，并用18 mm×18 mm的蓋玻片覆蓋；然后使用倒置光學顯微鏡(NikonEclipse TS100)和工業數碼相機(ToupTekTou Camucoms03100kpa)對活性污泥樣品進行圖像采集。為了提高活性污泥信息的代表性，每個活性污泥樣品使用3張載玻片進行形態學表征，并在總100×放大倍數下對載玻片上、中、下3個不同位置分別采集12張圖像，保存為2 048×1 536像素的TIF格式圖片，每個活性污泥樣品總共獲得108張圖片(12×3×3)。試驗期間，得到91個活性污泥樣品，共19 656張圖片(108×91×2)。

1.3.2 圖像處理

根據Amaral等[15]開發的活性污泥絮體圖像處理程序，使用深度卷積網絡DeepLabv3+方法構建活性污泥絮體分割模型，實現活性污泥絮體的分割。首先，對活性污泥絮體圖片背景進行校正；然后，根據活性污泥絮體確定其二值圖像；最后，對活性污泥絮體二值化圖像的邊緣進行檢測，確定測量區域，并提取活性污泥絮體的形態參數。活性污泥絮體圖像處理的過程，見圖1。

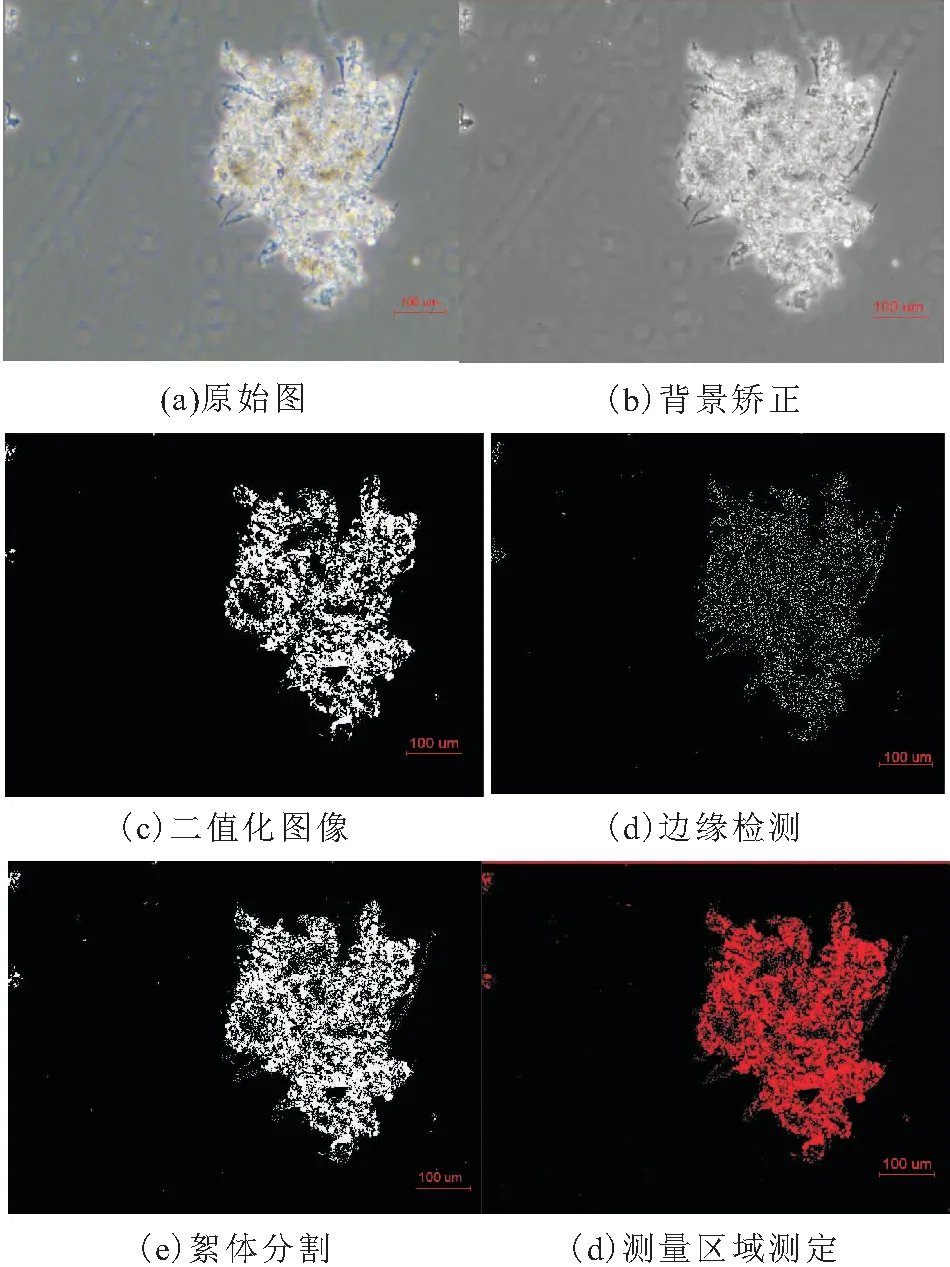
圖1 活性污泥絮體圖像處理的過程

在本研究中，基于do Amaral[8]對活性污泥絮體的研究，對選取的25個活性污泥絮體形態參數進行相關性分析，并去除多重相關系數大于|0.90|的變量和相關系數較低的變量，最終確定了14個活性污泥絮體形態參數，具體詳見表2。

表2 活性污泥絮體形態參數

1.4 偏最小二乘(PLS)法

偏最小二乘(PLS)法通過提取輸入矩陣X基本特征的線性組合，同時根據輸入矩陣X對輸出矩陣Y進行建模，是一種監測復雜過程的有效方法[17-18]。同時，PLS法也是一種兼顧多元線性回歸分析、典型相關分析和主成分分析功能的多元統計分析方法，尤其適用于觀測數據(樣本量)較少的情況。PLS法除了可以建立更為合理的回歸模型，還可以提供更大、更深層次的信息。

本文采用PLS法使用SIMCA軟件對內、外回流污泥絮體形態參數與好氧池出水水質指標(CODe、BODe、TNe和TPe)進行PLS回歸分析，分別建立了內回流污泥回歸模型(PLS1模型)和外回流污泥回歸模型(PLS2模型)，并通過擬合系數R2和預測系數Q2來判斷兩個回歸模型的適用性，最后根據預測系數Q2來確定最佳擬合模型。

擬合系數R2表示因變量與所有自變量之間的總體關系，可以體現出對回歸模型的解釋能力，其計算公式為

(1)

式中：SSR表示回歸平方和；SST表示總平方和。

預測系數Q2表示對因變量的預測能力，其計算公式為

(2)

式中：PRESSh為每一個維度的預測誤差平方和；SSh-1為前一個維度的殘差平方和[19]。

一般認為，當R2>0.5且Q2>0.5時，回歸模型的擬合效果較好[20]。在本研究中，輸入矩陣X包含表1中9個污水處理廠運行參數和表2中14個活性污泥絮體形態參數；輸出矩陣Y由好氧池出水水質指標CODe、BODe、TNe和TPe組成。本次試驗共得到91個活性污泥樣本，使用前80個活性污泥樣本作為訓練集，其余11個活性污泥樣本作為驗證集用于驗證回歸模型的預測效果。

2 結果與討論

2.1 PLS模型的建立

基于PLS法的建模原理，根據預測系數Q2來確定需要提取的主成分的個數，當所提取的主成分Q2<0時，停止提取。提取主成分的目的是盡可能地保留數據本質屬性，尋找原數據的內在低維結構，從而采用低維數據表征原數據，為后期研究分析提供依據。

對于內回流污泥模型(PLS1模型)，共提取4個主成分，輸出矩陣Y的累計擬合系數R2=0.752，累計預測系數Q2=0.694；對于外回流污泥模型(PLS2模型)，共提取4個主成分，輸出矩陣Y的累計擬合系數R2=0.775，累計預測系數Q2=0.720。兩個回歸模型輸出矩陣中輸出變量的R2和Q2值，見表3。

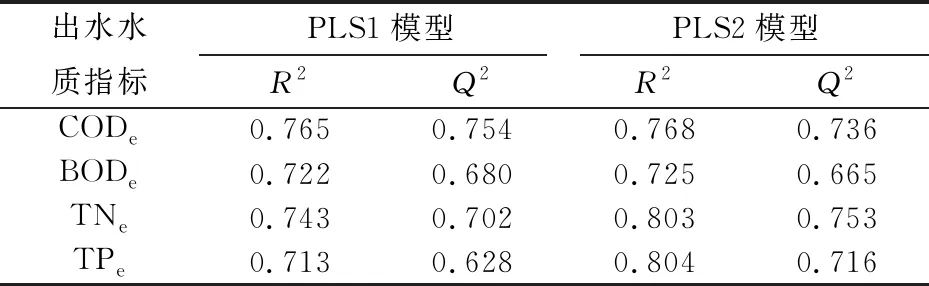
表3 PLS1模型和PLS2模型出水水質指標的擬合系數R2和預測系數Q2

由表3可知，兩個回歸模型對于出水中各輸出變量的預測系數Q2相差不大，但PLS1模型對于CODe、BODe有更好的預測能力，而PLS2模型則對TNe、TPe有更好的預測能力。

2. 2 模型擬合及預測效果評價

為了驗證回歸模型的預測效果，使用相對誤差r和確定性系數dy來確定回歸模型的擬合及預測程度。模型的相對誤差越小，確定性系數越大，表示回歸模型預測得越準確。相對誤差r和確定系數dy的計算公式如下：

(3)

(4)

為了分析兩個回歸模型的擬合效果，將PLS1模型和PLS2模型訓練集樣本的預測值與實測值進行了對比，見圖2。

由圖2可見，兩個回歸模型對輸出變量的預測能力大致相同，但是從相對誤差數據的波動來看，PLS2模型相對誤差數據的波動要小于PLS1模型，即從模型的擬合角度來看，PLS2模型的擬合效果要稍優于PLS1模型。

為了分析兩個回歸模型的預測效果，將驗證集樣本分別代入PLS1模型、PLS2模型計算其預測值，并與實測值進行了對比，見圖3。

由圖3可見，兩個回歸模型中CODe、BODe、TNe、TPe預測值與實測值的變化趨勢基本一致，這意味著通過活性污泥絮體形態參數預測出水水質具有可行性，表明模型有著很好的預測能力。

PLS1模型和PLS2模型訓練集和驗證集的合格率E(即小于給定相對誤差的樣本數占總樣本數的百分比)和確定性系數dy,見表4。

由表4可知，兩個回歸模型訓練集和驗證集的確定性系數dy都達到了0.60以上，說明兩個回歸模型對出水水質均有較好的預測效果；但是從對比情況來看，在PLS2模型中CODe、TNe、TPe的確定性系數dy均高于PLS1模型，且合格率E<20%的樣本比例更高，說明PLS2模型的計算結果更為可靠，證明從活性污泥絮體微觀角度建立出水水質預測模型的可行性。通過該模型，可以更好地指導實際污水處理設施的運行，從而為污水處理廠水質監測提供理論依據。

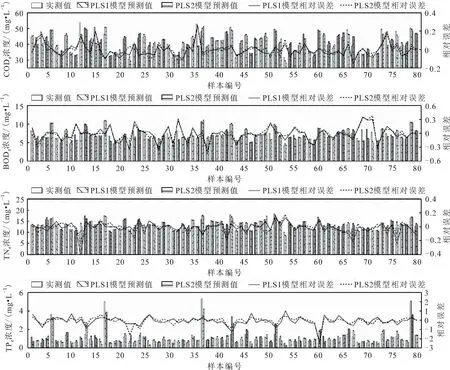
圖2 PLS1模型和PLS2模型訓練集樣本的預測值與實測值的比較

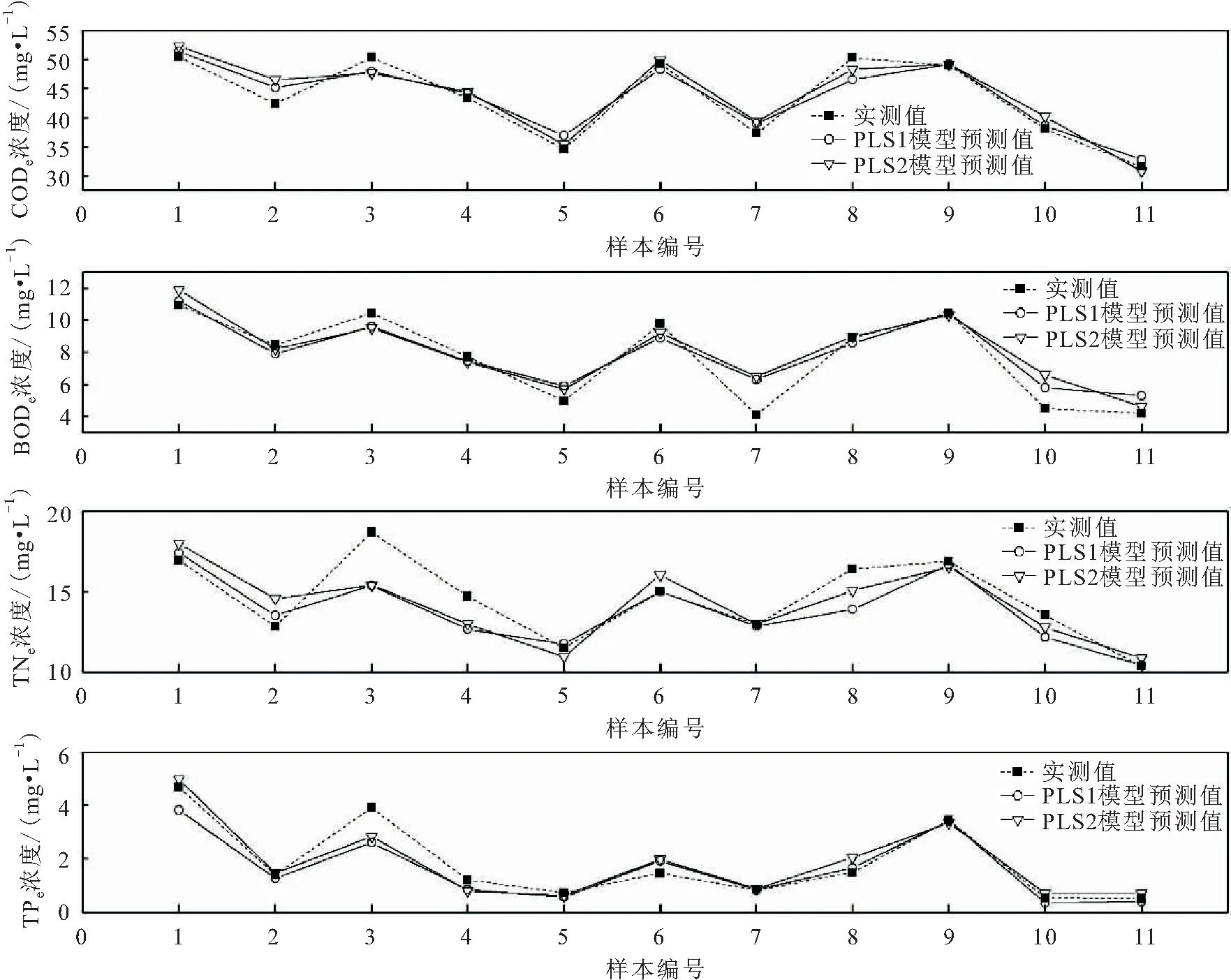
圖3 PLS1模型和PLS2模型驗證集樣本的預測值與實測值的比較

表4 PLS1模型和PLS2模型出水水質指標的擬合及預測效果對比

2. 3 數據相關性分析

2.3.1 輸入變量之間的相關關系

活性污泥絮體的形態特征與污水處理廠運行參數密切相關，為了研究它們之間的關系，對它們之間的相關關系進行了討論，各參數間相關系數取絕對值后得到的相關系數矩陣，見圖4。

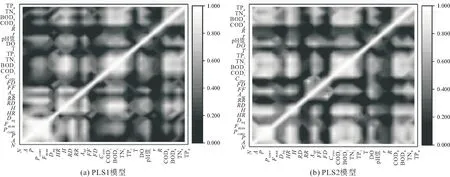
圖4 PLS1模型和PLS2模型輸入變量與輸出變量之間的相關系數矩陣圖

由圖4可以看出：

(1) 總的來看，活性污泥絮體不同形態參數間具有一定的相關關系。其中，用于表征絮體數量的參數N與用于表征絮體大小的參數A、P、Pconv、Fmax、Deq之間呈負相關關系，相關系數絕對值大于0.6(p<0.05)；表征絮體密實度、絮體大小和絮體規則性的參數之間也同樣具有較強的相關關系(相關系數>0.5，p<0.05)。由此來看，在不同的客觀條件下，表征絮體大小、絮體密實度和絮體規則性的參數變化較為同步。另外，進水水質指標之間也存在著較強的相關關系，其中CODi、BODi、TNi之間的相關系數都在0.85以上(p<0.05)，說明進水中污染物成分較為穩定。而好氧池運行參數T、pH值與活性污泥絮體形態參數之間的相關關系較為一般，推測變量T和pH值并沒有達到能夠顯著影響活性污泥絮體微觀特征的水平。

(2) 對比來看，PLS2模型中輸入變量之間的相關性更強，除了變量RD、RR、FD和R外，其他變量之間均具有較好的相關性(相關系數>0.5，p<0.05)。通過對比分析發現，對于內回流污泥，當絮體面積較大時，絮狀物的密實度和圓度也較高；而對于外回流污泥，絮體面積越大，絮狀物的密實度和圓度則越低。這可能與好氧池和二沉池的環境狀態有關，在好氧池中，好氧微生物快速生長，所以內回流污泥較為緊實；在二沉池中，相比于污泥中的其他微生物，絲狀菌對水中DO、有機碳源有更強的競爭能力，絲狀菌的繁殖同樣會導致絮體面積增大，但此時絮體的密實度會下降，嚴重時還會影響二沉池內泥水分離，導致出水水質惡化。

2.3.2 輸入變量與輸出變量之間的相關關系

表5列出了部分輸入變量與輸出變量的相關系數，從表中刪除了輸入變量RR、FD、T、pH值、r、R，因為它們與輸出變量沒有顯著的相關性。

由表5可知，外回流污泥絮體形態參數與出水水質指標之間的相關性更強，在所篩選的變量中，絮體的密實度參數(孔率HR)、進水水質指標(CODi、BODi、TNi)與出水水質指標之間的關系更加密切。

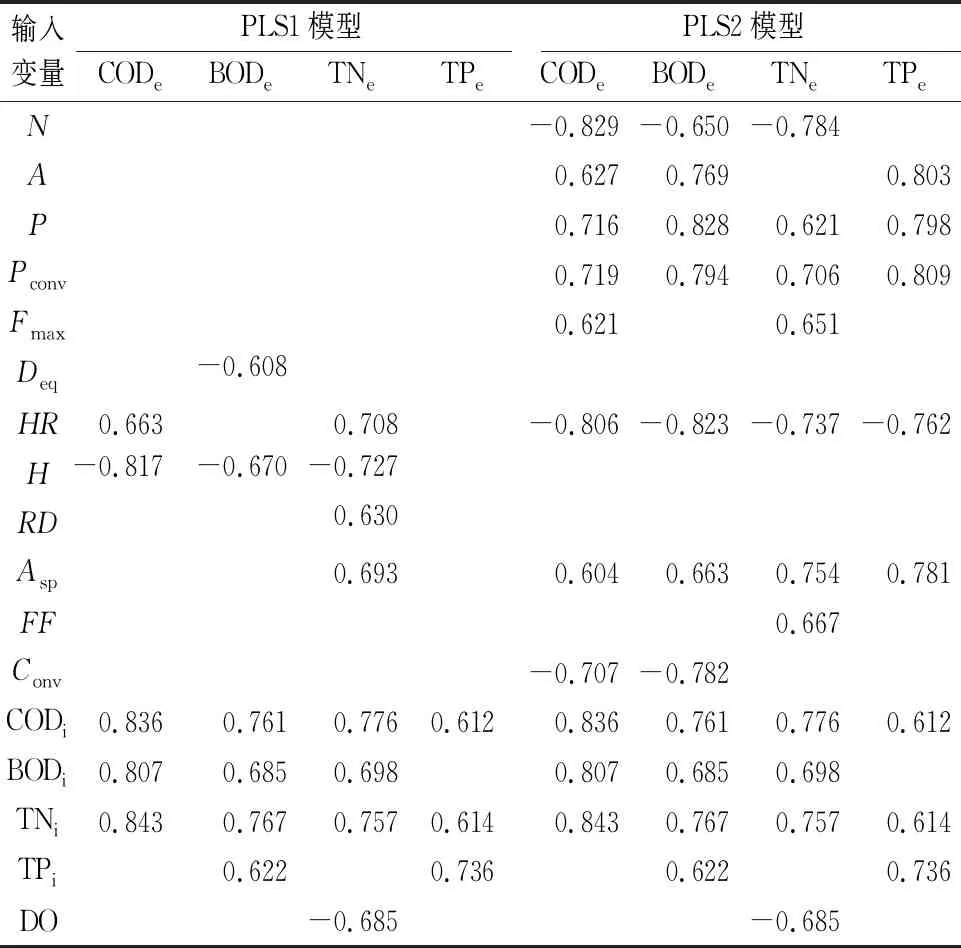
表5 PLS1模型和PLS2模型輸入變量與輸出變量之間的相關系數

具體來看，對于COD、BOD來說，它們都表示水中有機物的含量，活性污泥絮體中微生物將有機物作為碳源，將其降解為無機物或合成自身細胞，從而去除水體中的有機物。在PLS1模型中，CODe、BODe與絮體密實度參數孔率HR呈正相關關系，與變量絮體密實度參數孔數H呈負相關關系，說明當活性污泥絮體結構緊密、內部孔洞數量少時，出水中CODe、BODe含量高。這主要是因為在活性污泥中，菌膠團細菌為嚴格好氧菌，絲狀菌是好氧和微量好氧菌，而內回流污泥中DO含量較低，所以絲狀菌呈優勢生長，造成絮體面積增大，引起污泥膨脹現象，致使出水水質變差[21]。與此同時，大量菌膠團會通過膠質狀胞外多聚物(EPS)黏附在絲狀菌上，由于細菌相互堆積，會導致絮體密實度增加。另外，CODe和BODe與CODi、BODi、TNi呈正相關關系，說明CODe和BODe很大程度上取決于進水污染物的濃度。在PLS2模型中，CODe、BODe與選擇的輸入變量都有一定的相關性，但值得注意的是，與PLS1模型不同，在PLS2模型中，CODe、BODe與HR呈負相關關系。

TN表示水體中各種有機氮和無機氮的總量，其主要通過硝化反硝化去除。在PLS1模型中，TNe與HR呈正相關關系，與DO呈負相關關系。在活性污泥法中，一般要求內回流污泥中DO含量在0.5 mg/L以下，當內回流污泥中DO的含量較高時，會影響反硝化細菌的脫氮過程[22]。而對于PLS2模型來說，TNe與HR呈負相關關系。當活性污泥絮體密實度較低，外回流污泥孔洞內部攜帶的DO會造成異氧菌大量繁殖，消耗有機碳源，引起后段反硝化碳源不足，影響反硝化的正常進行，導致出水中TNe含量升高[23]。

磷對微生物生長至關重要，當水體中磷含量超過0.2 mg/L時，會引起水體的富營養化。在PLS1模型中，僅TPe與進水參數的相關性較大，這主要是因為內回流污泥主要是起到脫氮的作用，與除磷效果的相關關系較弱。而在PLS2模型中，TPe與多個輸入變量呈較強的相關關系，這是因為外回流污泥中攜帶的硝酸鹽氮含量會影響聚磷菌的釋磷過程，從而影響后續的除磷過程[24]。

3 結 論

(1) 在本試驗中，分析了內、外回流污泥絮體形態參數與好氧池出水水質指標的關系，并結合污水處理廠運行參數對出水中CODe、BODe、TNe、TPe進行了預測，并通過對比PLS1模型與PLS2模型的擬合效果和預測效果，結果發現PLS2模型的擬合效果和預測效果均要優于PLS1模型。其中，PLS2模型對CODe、BODe、TNe、TPe的預測系數Q2分別為0.736、0.665、0.753、0.716，表明該模型具有良好的預測效果，可以更好地指導實際污水處理設施的運行，為污水處理廠的水質監測提供了一種新的方法。

(2) 通過對模型的驗證，結果發現PLS1模型和PLS2模型兩個回歸模型驗證集的確定性系數都達到了0.60以上，說明兩個回歸模型對出水水質指標均有較好的預測效果，證明了從活性污泥絮體微觀角度建立水質預報模型的可行性。但是對比來看，PLS2模型中的確定性系數均高于PLS1模型，且E<20%的樣本比例更高，說明PLS2模型的計算結果更為可靠。

(3) 相關性分析表明：在PLS1模型中，當活性污泥絮體面積越大、密實度越高、形狀越規則時，出水中CODe、BODe、TNe、TPe越高；在PLS2模型中，當活性污泥絮體面積越大、絮體密實度越低、絮體形狀與圓偏差越大時，出水中CODe、BODe、TNe、TPe越高。在實際污水處理廠的運行中，一方面可以對這些活性污泥絮體的形態參數進行分析，判斷出水水質；另一方面，可以通過調整模型中提及的運行參數，來改善出水水質。