基于智能電表的量測數據實時狀態監測估計

王 坤，趙永生，趙愛華，余小飛，張 緯

(1.國網安徽省電力有限公司，安徽 合肥 230000；2.國網安徽省電力有限公司 電力科學研究院，安徽 合肥 230601；3.國網安徽省電力有限公司 亳州供電公司，安徽 亳州 236800；4.國網安徽省電力有限公司 阜陽供電公司，安徽 阜陽 236001)

配電網已從傳統無源電網轉向高度復雜的有源電網。在這種背景下，分布式電源的集成將使配電網的運行瀕臨極限，面臨非計劃停電的風險。因此基于實時狀態估計方法實現配電網運行狀態的快速感知已成為供電公司較為迫切的需求[1-4]。

配電網的實時狀態估計需要以高分辨率的測量數據為基礎。配電網中已經部署了大量智能電表，能夠采集海量的測量數據。但是智能電表的測量數據主要被用來計算電費，因此其數據采集周期一般設定為每天采集3～4次，這顯然遠遠不能滿足實時狀態估計的要求[5-6]。由于PMU能夠提供高時間分辨率的測量數據，因此現有電網實時狀態感知方法大多是基于PMU測量數據[7-9]。但是在配電網中使用這種方法顯然將面臨部署大量PMU的成本，不具備大規模推廣的可行性，為此提出一種基于智能電表的實時配電網狀態估計的低成本解決方案。智能電表所采集的數據存在時間分辨率較低的問題，因此使用部署在中低壓變電站的PMU所提供的高時間分辨率的測量數值對智能電表的測量數據進行插值處理，以提高智能電表測量值的時間分辨率。仿真分析結果表明，該方案能夠以較低的成本有效提升配電網狀態估計的實時性。

1 加權最小二乘狀態估計

加權最小二乘狀態估計是常用的電力系統狀態估計方法[10-12]。在加權最小二乘狀態估計公式中，狀態變量與可用測量向量的數學關系：

z=h(x)+e

(1)

式中：z是一個包含所有可用測量值的向量；h(x)是一個包含非線性函數的向量，其中非線性函數在數學上將狀態變量與測量值相關聯；x是狀態向量；e表示影響測量值的高斯噪聲(即測量誤差)。加權最小二乘狀態估計法通過最小化j(x)獲得狀態向量：

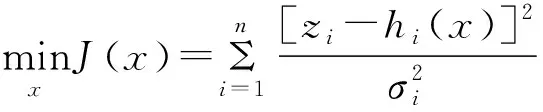
(2)

式中：n是測量值的總數；σi是與測量值相關的標準偏差；R是用于測量值加權的測量誤差協方差矩陣。

2 狀態估計方法

基于智能電表測量值的配電網狀態估計方案如圖1所示。

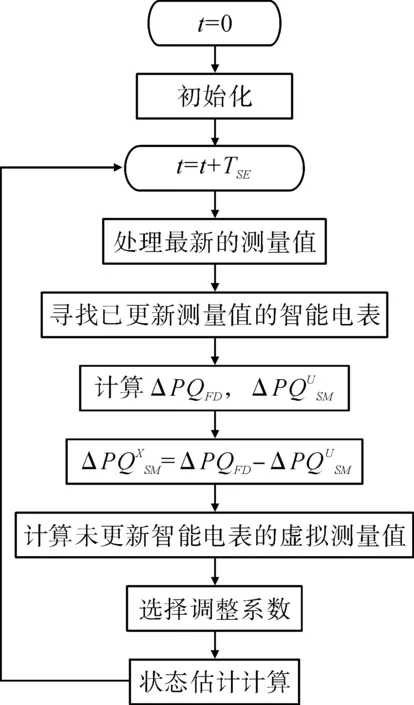
圖1 監測方案流程Fig.1 Monitoring program process

2.1 系統狀態初始化

假設所有測量值在t= 0 s時可用，使用可用測量值進行初始狀態估計；然后存儲初始估計電壓狀態，以便可以在下一個狀態估計過程中使用。此外，所有智能電表和PMU的功率測量值都將被存儲，以便在之后的狀態估計過程計算饋線負載偏差。

2.2 測量值更新

在每次狀態估計過程中，都要考慮來自智能電表的最新測量值，以便計算與先前估計過程(t-TSE)中對應饋線負載的變化。

2.3 查找與計算周期同步更新的智能電表

完成初始狀態估后，智能電表會按照大于計算周期的頻率更新測量值。將在周期TSE已同步更新其測量值的所有智能電表標識在集合U中；N是包含所有智能電表的集合，則U?N。在周期TSE未同步更新其測量值的其余智能電表包含在集合X中。

2.4 計算饋線的負載偏差

在初始化后的每個狀態估計過程中首先計算饋線的負載變化。基于PMU的測量值，在計算周期TSE內的低壓饋線負載變化計算方法如下：

(3)

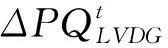
(4)

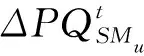
(5)

2.5 估算與計算周期不同步更新的智能電表測量值

(6)

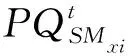
在單個智能電表數據更新周期內，配電網的饋線電壓值可能會發生較大變化。為了使電壓估計值盡可能準確地跟蹤饋線電壓變化，需要將前一次的電壓估計值視作當前未更新的電壓測量值：

(7)

2.6 調整參數

常規最小二乘狀態估計算法的測量權重由表征每個測量設備的方差的倒數來定義。但由于智能電表的測量數據難以和計算周期同步，這意味著在智能電表測量值未更新的時間段內，系統真實狀態值可能會發生顯著變化，因此需要將測量值異步性引入測量值方差的調整。測量值方差的調整方法為：

(8)

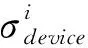
2.7 進行狀態估計

首先準備2種類型測量值，即智能電表的同步更新測量值和未同步更新的估計測量值分別通過式(6)和式(7)計算得出；然后，將完整的測量向量用于加權最小二乘狀態估計算。配電網的估計電壓狀態以及來自智能電表測量的功率測量值將被臨時存儲，以便將其用于下一次狀態估計。

3 仿真分析

3.1 測試系統

在MATLAB/Simulink實現如圖2所示的測試系統。

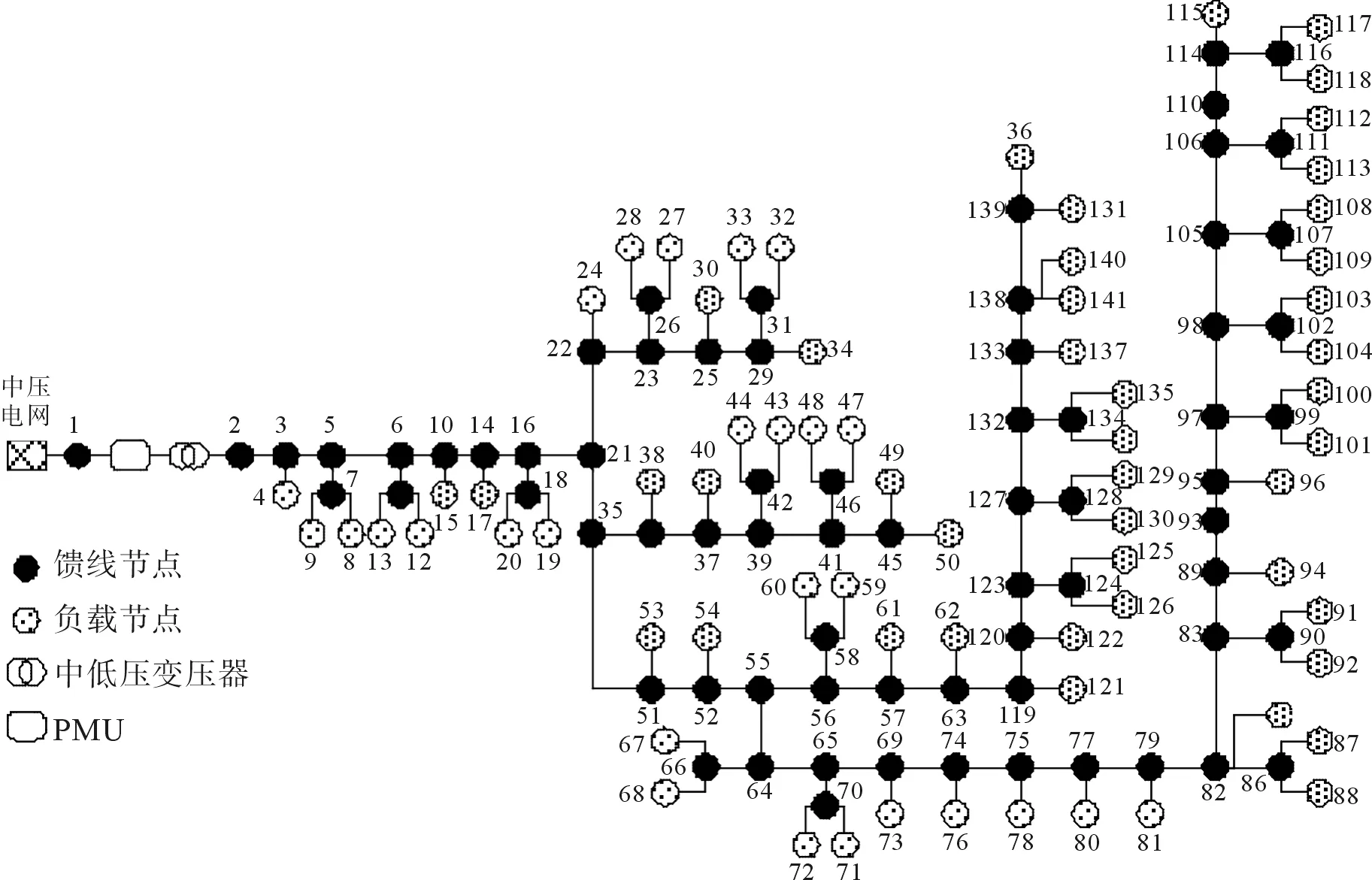
圖2 測試系統Fig.2 Test system

在測試系統負載節點中一共設置70個智能電表，每個智能電表都提供對應節點的有功測量值和無功測量值以及電壓幅值，并按照圖3所示的模式更新測量值。

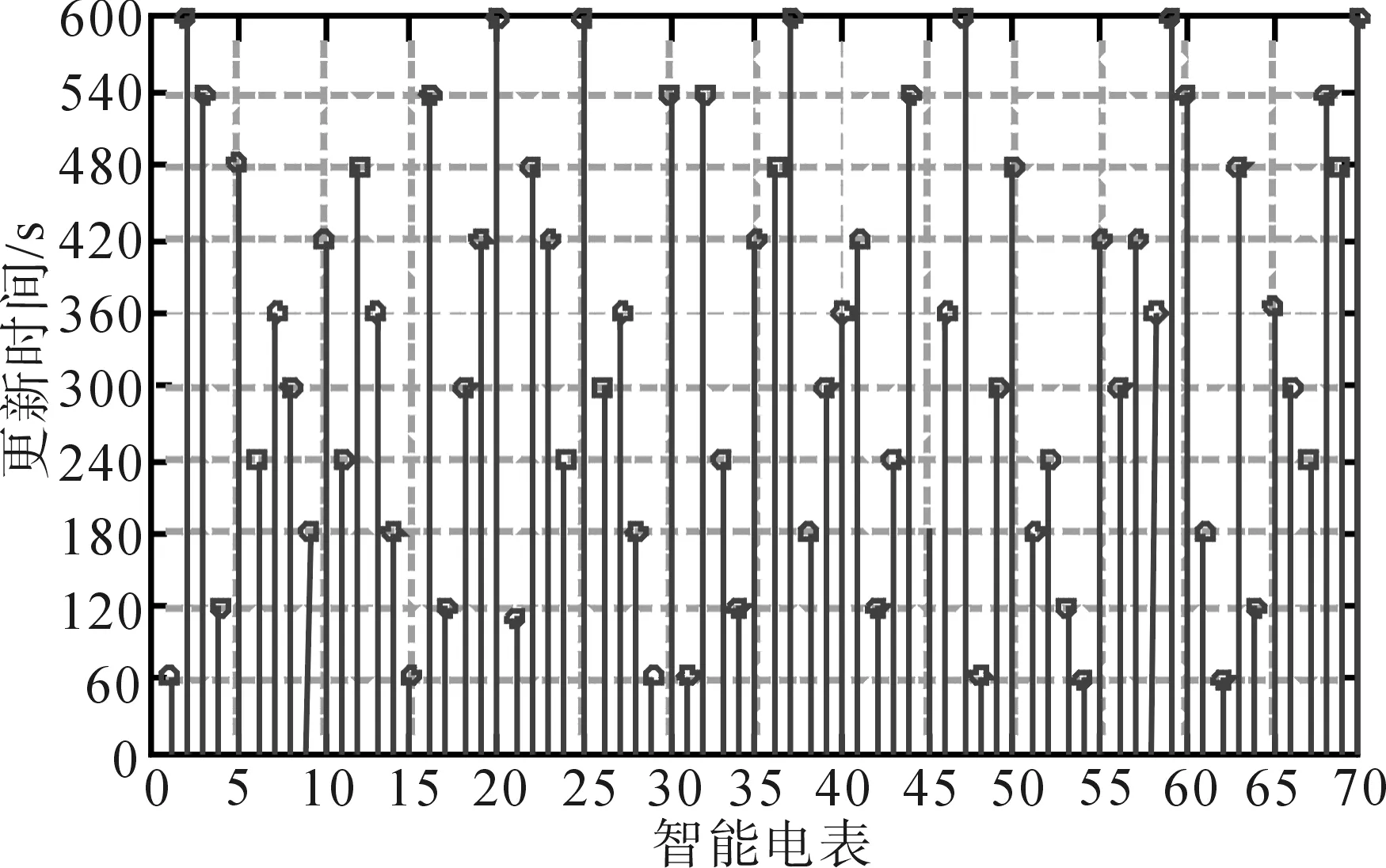
圖3 智能電表測量值的更新時間Fig.3 Update time of smart meter measurement value

表1根據智能電表的標稱電流(In)，給出了各種精度等級的智能電表的測量誤差(占滿度電表讀數的百分比)。在以下仿真實驗中使用的測量值是按照下式通過將由模擬系統得出的真實測量值疊加到高斯測量噪聲N(0,σ)上而創建：

Zmeavs=ztrue+FS·N(0,σp,Q,|V|)

(9)

式中：Ztrue是模擬系統得出的真實測量值；FS是不同測量儀表(8.8 kVA和220 V)的滿量程讀數；σp,Q,|V|是和智能電表精度等級相對應的標準測量偏差。

在仿真實驗中，假設智能電表每10 min(TSE= 10 min)更新一次其測量值。圖3給出了針對單個時間間隔內智能電表的數據更新模式。通過向每個智能電表隨機分配TSE的整數倍來創建此數據更新模式[13]。在每個數據更新周期結束后，將TSE添加到新的更新周期中，以便獲取下一個周期的每個智能電表的數據更新時間。

表1 智能電表的標準測量誤差Tab.1 Standard measurement error of smart meter

為了評估所提出的監測方案的性能，實驗實現了常規狀態估計方案，用于比較和驗證本方案。在常規方案中，僅在智能電表數據更新周期結束時使用加權最小二乘法進行狀態估計，并且只考慮與計算周期同步的智能電表測量值。使用真實電表測量值繪制每個用戶(對應圖4中的負載節點)的負載曲線。真實電表測量值數據來自60多個真實電力用戶的用電記錄。有功功率和無功功率的測量精度分別對應表1所示的智能電表精度等級0.5和1，電壓測量誤差為滿量程電表讀數的0.5%。

3.2 調整參數

上面提到的2對調整參數對狀態估計結果影響較大，需要進行慎重選擇。對不同的調整參數組合的平均2范數和平均最大范數估計誤差進行仿真測試，結果如圖4所示。實驗數據表明正確選擇調整參數可以顯著提高估計準確性。圖4中第1 247個參數組合對應的估計誤差最低，此組合的調整參數為kP=3，kV=2.5，aP=2和aV=2.5。使用該參數組合進行以下對比實驗。

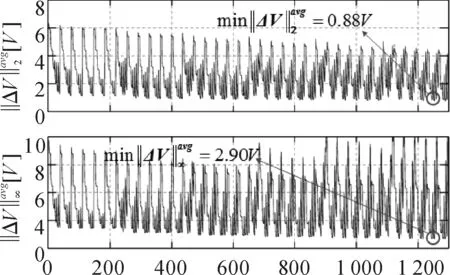
圖4 不同參數組合的影響Fig.4 Influence of different parameter combinations

3.3 結果分析

基于常規狀態估計方案和本文方案對圖2所示測試系統進行仿真分析，得出的二范數和最大范數估計誤差如圖5所示。

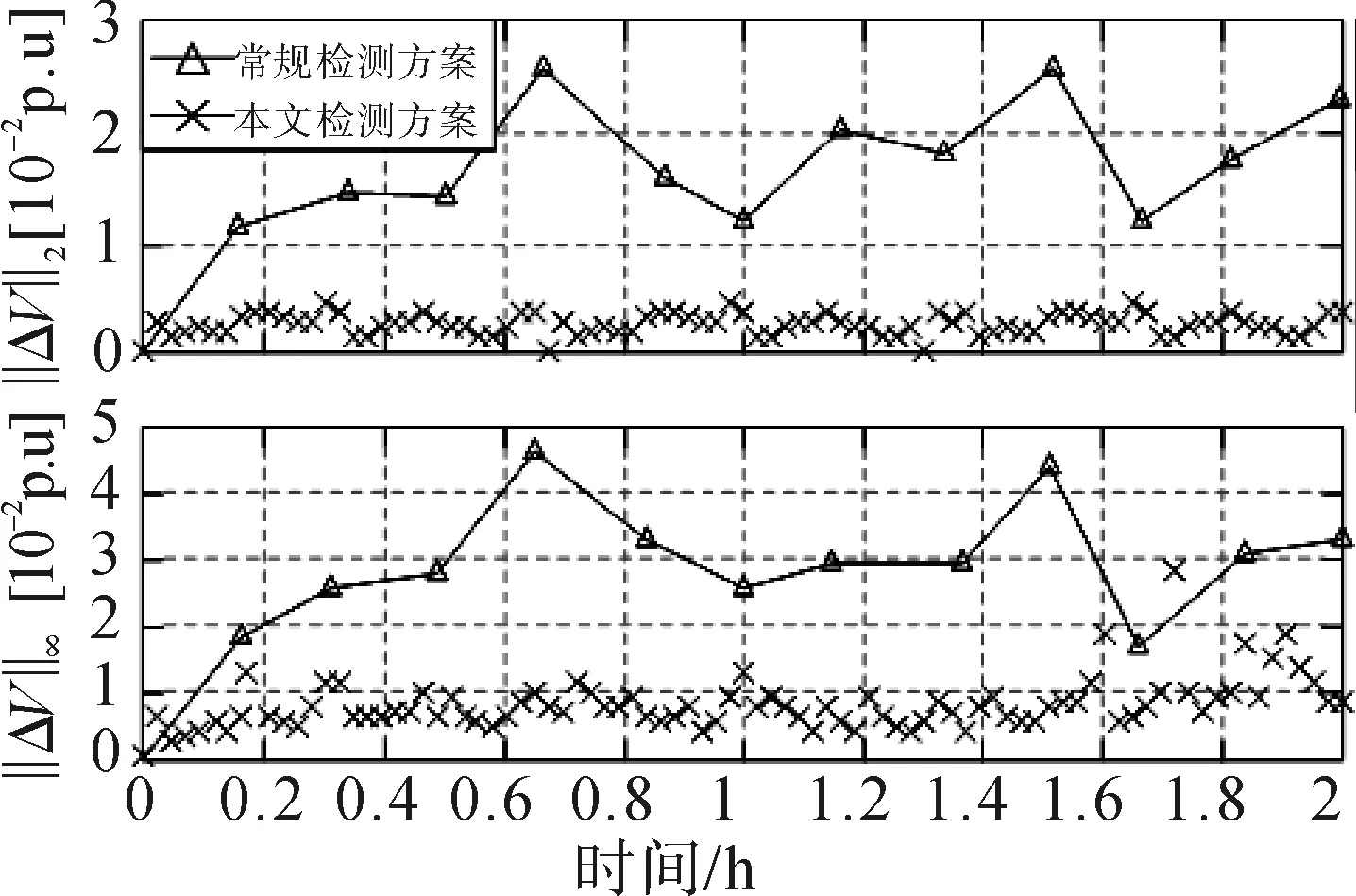
圖5 估計誤差Fig.5 Estimation error

本方案所使用的智能電表數據更新間隔是1 min，常規方案則是10 min。從圖5可以看出，常規方案的誤差要明顯高于本方案，其主要原因是常規方案的數據刷新率較低。圖6給出了2種方案的在三相負載節點142上的估計電壓曲線。

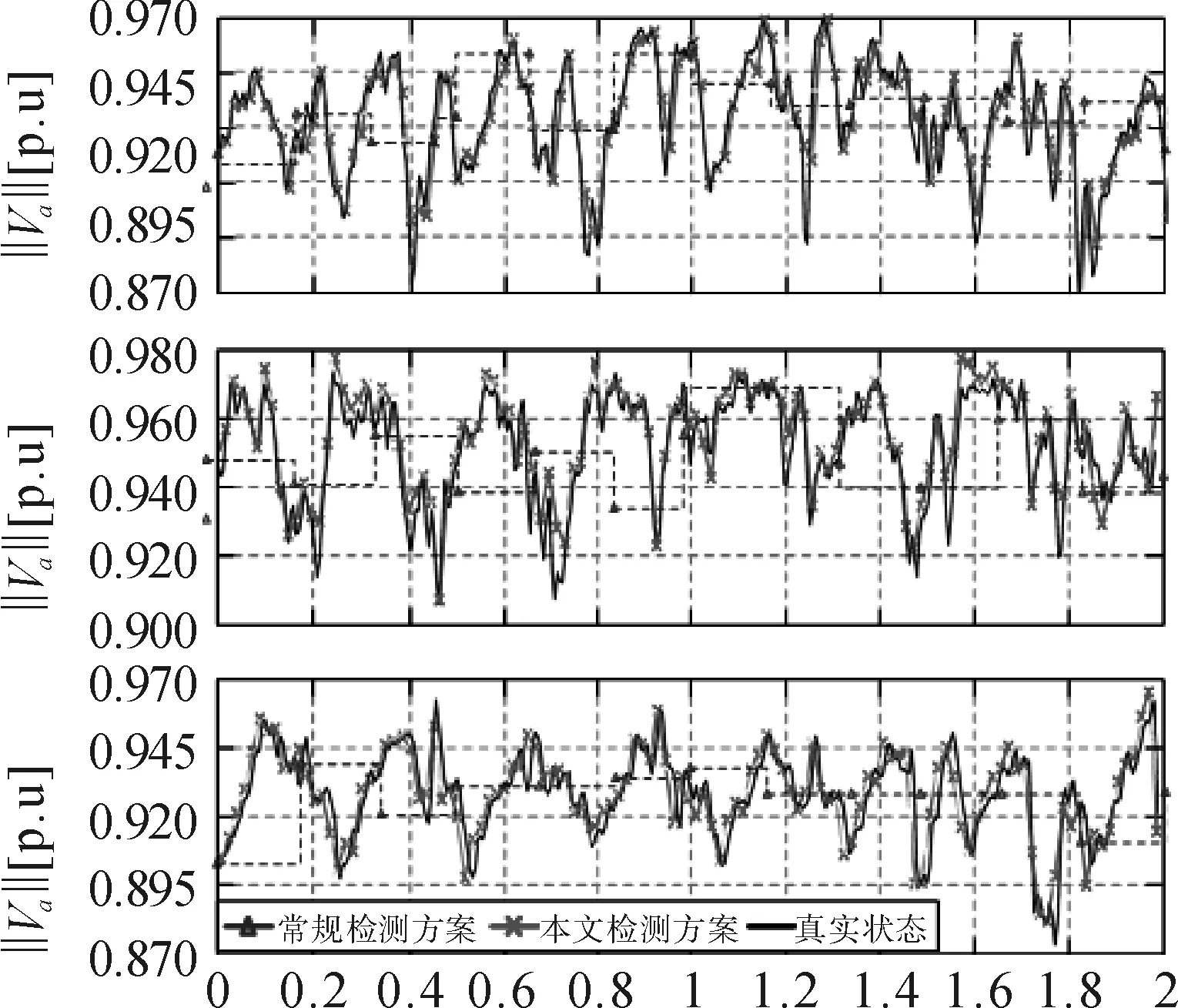
時間/h圖6 142三相負載的電壓曲線Fig.6 142 Voltage curve of three-phase load

Simulink模型的時間分辨率為20 s，而TSE=1 min，因此在本方案的2次計算之間，系統真實狀態將更新3次。從圖6可以看出，本方案的電壓曲線更加擬合真實曲線，主要原因是本方案的數據刷新率高于常規方案，且使用估計測量值也使得估計準確度得到提升。

在圖5的一些特殊情況下，本方案的估計誤差高于常規方案。這主要是由于在當前時間間隔中使用來自上一次估計計算所存儲的系統狀態值與系統的實際當前狀態明顯不同，因此在這種系統狀態，短時間被發生較大變化的情況下，本方案的估計準確性會降低。但是，在Simulink模型中使用的時間分辨率為20 s的負載曲線，而在幾秒鐘的時間內系統狀態發生這種變化的實際概率并不大，圖5和圖6的數據也證明了這一點。

為了驗證不同時間分辨率的測量值對本方案的狀態估計誤差影響，針對不同數據更新速率(5～30 min)進行對比仿真實驗，結果如圖7所示。

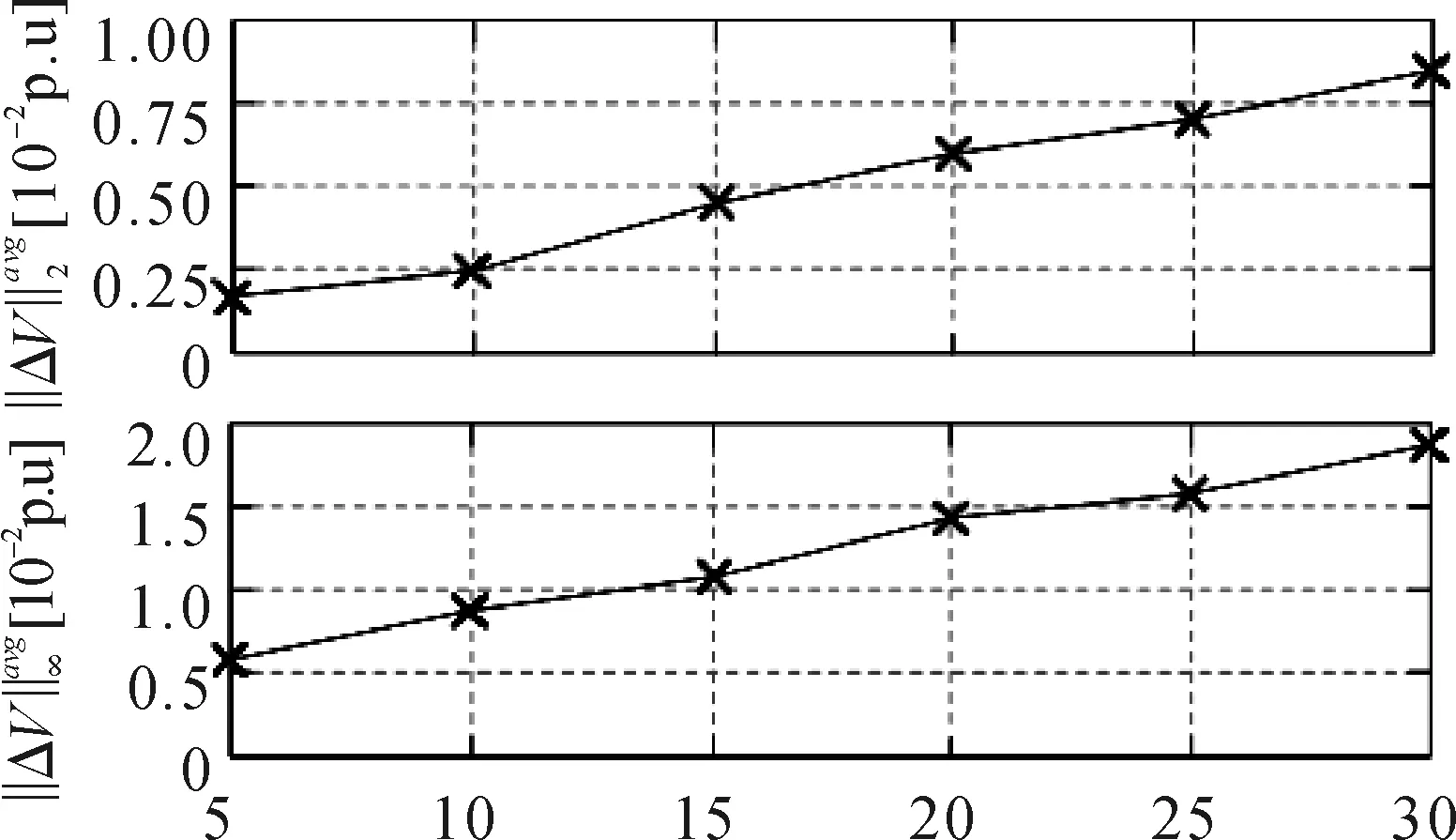
智能電表數據更新速率/min圖7 不同測量值更新速率的估計誤差Fig.7 Estimation error of update rate of different measured values

圖7針對不同的數據更新速率給出了2 h仿真時間內來自所有系統節點的平均二范數誤差和平均最大范數誤差。從圖7可以看出，智能電表的數據更新速率幾乎線性地影響了本方案的性能，對其進行分析可知，本方案在從20 min的更新速率時仍保持令人滿意的性能，而對于更低的更新速率而言，本方案雖然可以運行，但性能降幅較大。考慮到狀態估計結果將應用在不同的電壓等級配電網在線監測程序中使用，因此數據更新速率可以根據這些應用程序的具體要求來確定。

4 結語

為實現對配電網進行準確的狀態估計，提出了一種基于智能電表的低成本配電網狀態估計方案。仿真分析結果表明，盡管智能電表只能夠提供從5～30 min的測量數據更新速率，但所提出的狀態估計方案可以1 min的更新速率提供有關配電網運行狀態的準確信息。