連續油管滾筒多層纏繞力學分析與試驗研究

李心成，謝 猛，岳書常，于 曉，劉偉強

(煙臺杰瑞石油裝備技術有限公司，山東 煙臺 264034)

滾筒作為連續油管運輸及作業的關鍵部件之一[1]，對其進行配套開發以滿足深井、超深井連續油管作業要求是當前各大油氣公司的重點工作之一[2]。考慮到因連續油管循環彎曲、矯直塑性變形[3-5]導致的滾筒受力的復雜性，再加上我國山區道路條件的限制，準確地分析連續油管多層纏繞工況下滾筒的受力情況，保證其可運輸性及安全性也已成為滾筒設計的關鍵問題[6]。

楊高、羅剛[7]通過理論分析得到連續油管拉彎變形時截面彎矩、軸力及滾筒轉矩隨松弛角度變化的關系式。施志輝等[8]對連續油管在滾筒上彎曲與拉直狀態進行了分析，并給出能夠保證連續油管緊密纏繞及順利拉出的松弛角度。在文獻[7-8]基礎上，劉星[9]分析了多層連續油管纏繞后滾筒筒身及輻板的受力情況，得到滾筒所受徑向及軸向力的計算公式。在描述連續油管在纏繞等復雜應力狀態下的力學行為方面，Liu[10]及Tong[11]通過理論及仿真分析驗證了纏繞過程中軸力和彎矩是影響連續油管極限承載能力和壽命的重要因素。為了提高連續油管滾筒的容量，楊曉剛等[12]研究設計1種橢圓形滾筒，并通過仿真手段驗證了其設計方案的合理性。

盡管國內外許多學者在連續油管彈塑性、疲勞壽命、多層纏繞滾筒的受力分析等領域取得了一定的研究成果，由于連續油管本身的塑性變形特性以及多層纏繞復雜的應力狀態，再加上滾筒現場作業工況很難預測，現有多層纏繞系統理論不能完全真實反映連續油管滾筒的實際工作狀態。因此，從試驗角度修正現有理論成果顯得尤為重要。為此，本文在前人研究的基礎上，通過理論分析得到單層纏繞及多層纏繞下滾筒筒身所受徑向力、滾筒輻板所受軸向力及多層纏繞系數的計算公式，并以某連續油管運輸滾筒為例，計算得到多層纏繞狀態下各力學參數，最后通過仿真及試驗手段驗證了計算公式的有效性。

1 連續油管單層纏繞滾筒力學分析

按照純彎曲理論，任意縱向纖維的正應力與它到中性層的距離成正比[13]，當連續油管彈性區域高度de等于連續油管外徑d，即連續油管最外層剛好達到屈服極限時，連續油管中心軸線彈性范圍內的曲率半徑取得最大值[14]。文獻[7]通過理論分析證明，連續油管純彎曲時的彈性變形高度僅為其外徑的10%～15%，實際工程應用中可按照極限塑性變形對連續油管進行彎矩計算，但是拉彎導致的中性層偏移不能忽視，如圖1所示。

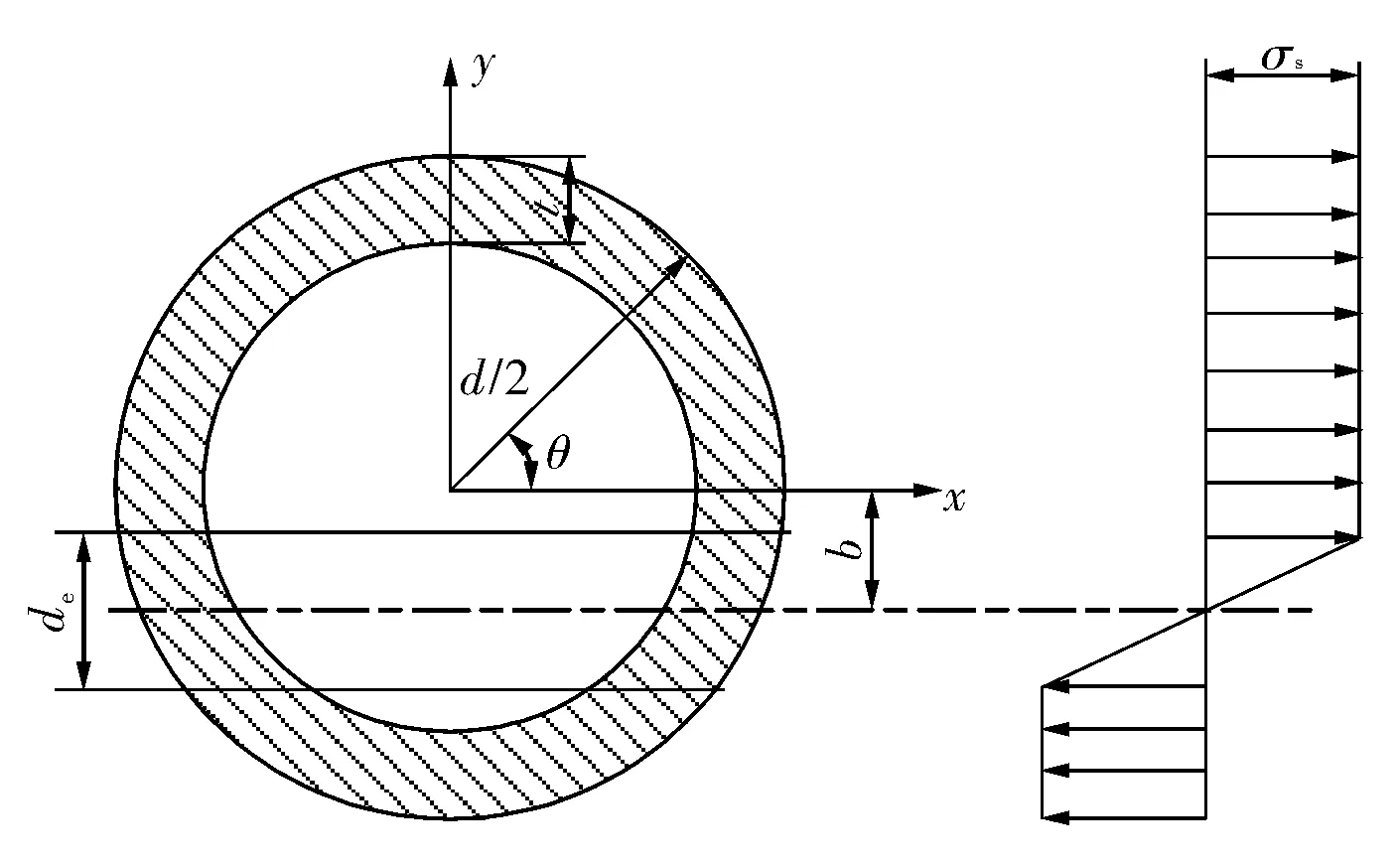
圖1 連續油管截面中性線偏移應力分布示意圖

此時軸力N和彎矩M分別為[7]

(1)

(2)

式中：d為連續油管外徑；t為連管油管壁厚；b為連續油管中性線偏移距離；E為連續油管彈性模量；σs為連續油管屈服極限；de為連續油管彈性區域高度，de=2Rbσ/E；Rb為連續油管彎曲半徑，第1層油管纏入時，Rb與滾筒筒身外徑R相等。

連續油管張緊且剛離開滾筒A點時，系統受力如圖2所示。

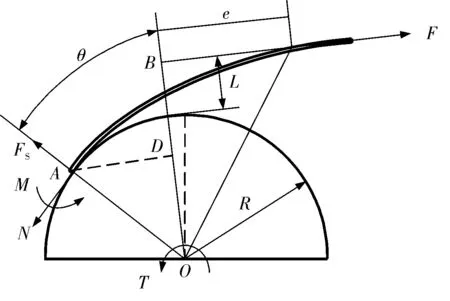
圖2 連續油管工作過程受力示意圖

此時連續油管截面彎矩M、軸力N及滾筒轉矩T之間的關系分別為[7]

(3)

(4)

式中：θ為連續油管松弛角度。

為了得到連續油管對滾筒的徑向壓力，取1/2連續油管滾筒模型，其受力如圖3所示。

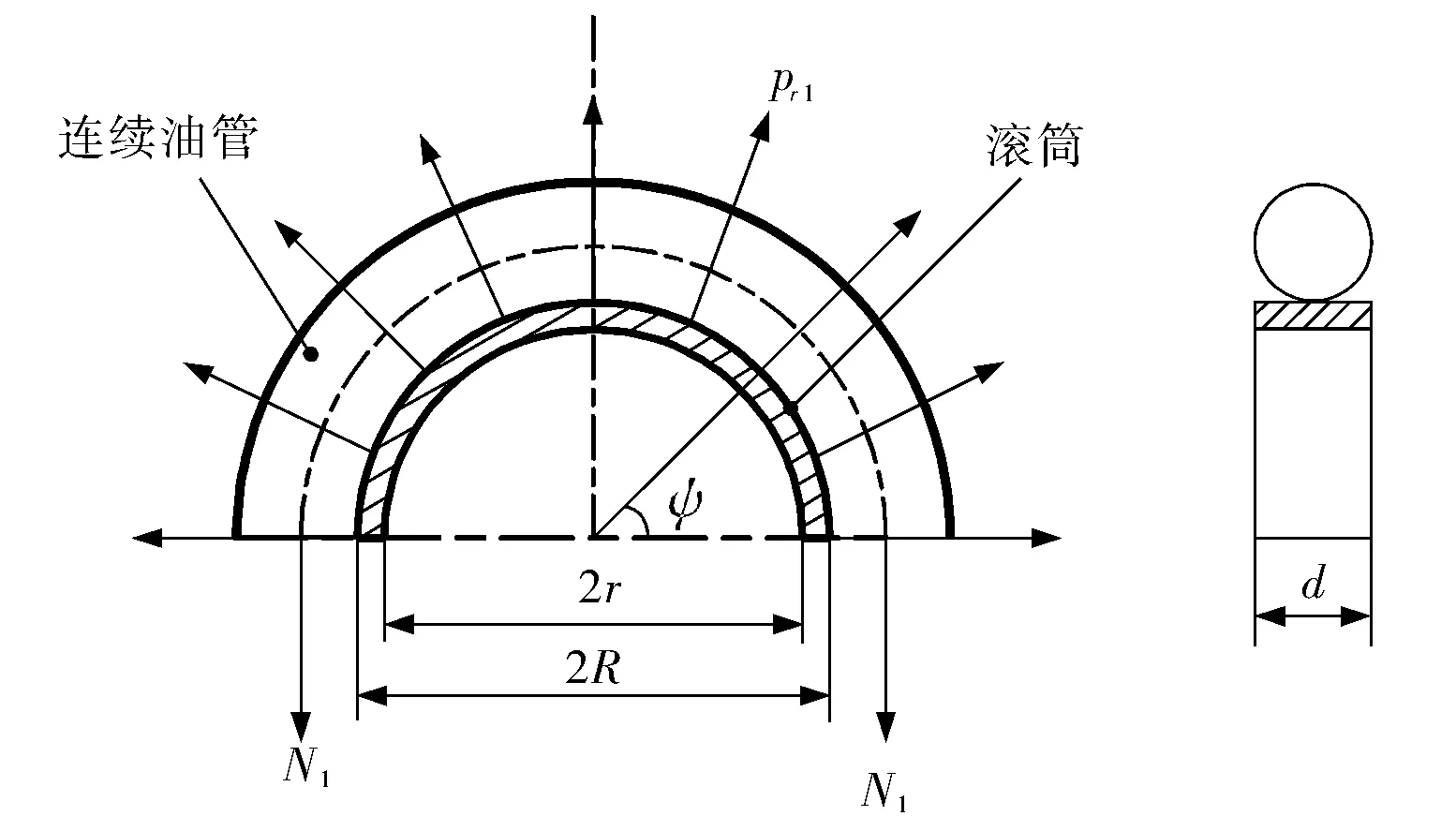
圖3 連續油管滾筒纏繞狀態受力示意圖

當連續油管緊密纏繞在滾筒上時，可近似認為連續油管對滾筒的壓力均勻作用在寬度為d的圓環上[15]，此時連續油管對滾筒輻板的軸向力Fa1為零。取一段連續油管(其對應圓心角為ψ)微段dψ，此時滾筒所受徑向壓力pr1與第1層連續油管纏繞軸力N1之間的關系為

(5)

即

(6)

2 連續油管多層纏繞滾筒受力分析

連續油管在滾筒上進行多層纏繞時，外層連續油管纏繞在內層連續油管形成的管縫上，連續油管呈“金字塔”形堆疊在滾筒上，如圖4所示。事實上，隨著滾筒纏繞層數的增加，連續油管彎曲半徑Rb隨之增加，滾筒筒身的徑向變形u也隨之變化，為作區分，將第n層連續油管軸力表示為Nn，將第n層連續油管纏入后，滾筒筒身的徑向變形表示為un。

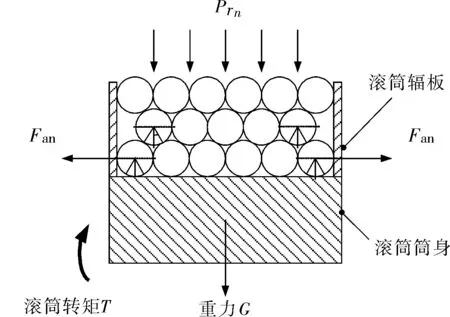
圖4 連續油管多層纏繞滾筒受力示意圖

當滾筒纏繞2層連續油管時，滾筒筒身所受徑向壓力pr2、滾筒輻板受到的軸向力Fa2及滾筒筒身的徑向變形u2分別為[9]

(7)

(8)

(9)

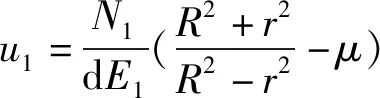
當滾筒纏繞n(n≥3)層連續油管時，滾筒筒身所受徑向壓力prn、滾筒輻板受到的軸向力Fan及滾筒筒身的徑向變形un分別為[9]

(10)

(11)

(12)

式中：k為連續油管層數；A為連續油管橫截面積。

考慮到SY/T 6698—2007《油氣井用連續管作業推薦作法》中要求R≥ 20d，保守考慮取R=20d，故式(6)、(10)、(11)變為

(13)

(14)

(15)

在設計連續油管滾筒時，通過上述公式計算滾筒所受徑向壓力較為繁瑣。為了工程計算的便利性，將n(n≥3)層連續油管纏繞時滾筒所受徑向壓力與單層連續油管纏繞時滾筒所受徑向壓力的比值、n(n≥3)層連續油管纏繞時滾筒輻板所受軸向力與2層連續油管纏繞時滾筒輻板所受軸向力的比值分別定義為多層纏繞系數λ1、λ2[16]，即

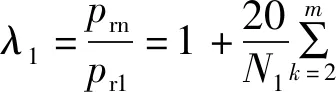
(16)

(17)

基于上述理論，以杰瑞某連續油管運輸滾筒(相關參數如表1所示)為例進行計算，得到各力學參數，如表2所示。

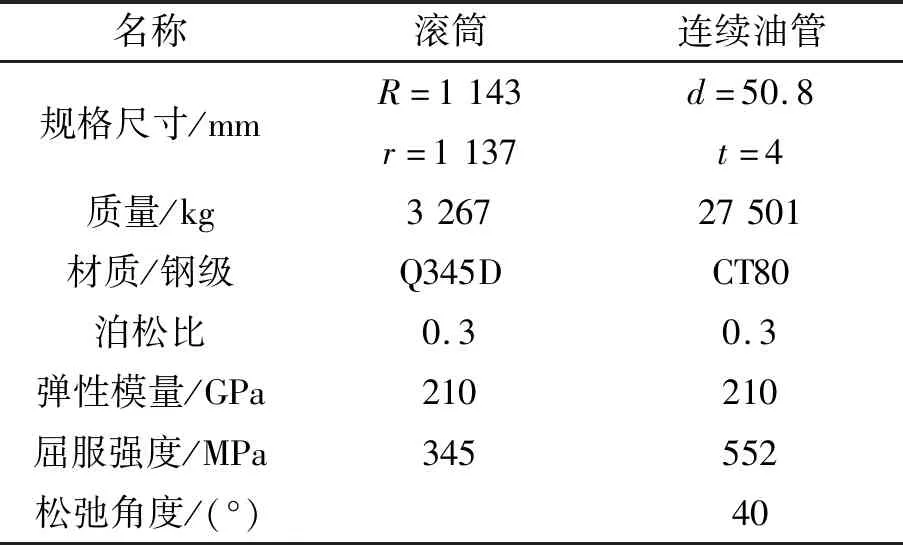
表1 杰瑞某連續油管運輸滾筒參數

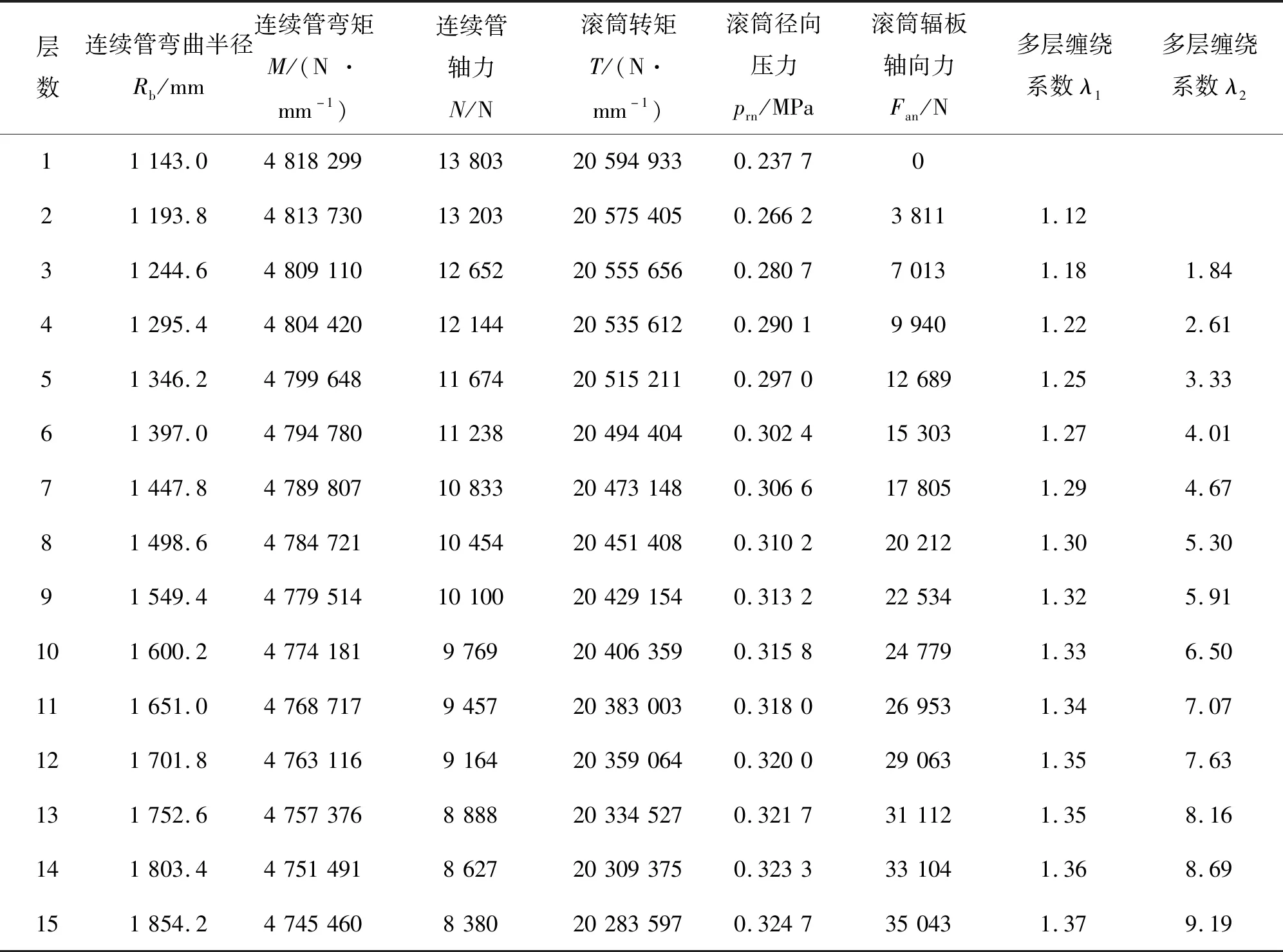
表2 不同纏管層數下滾筒力學參數計算結果

由表2可以看出，截面彎矩對于纏繞層數變化的敏感度較小，不同纏繞層數對截面軸力的影響較大。當第1層連續油管纏繞到滾筒上時，由于連續油管本身的張力作用，連續油管對滾筒筒身產生徑向壓力。當多層連續油管纏繞時，作用于滾筒筒身的徑向壓力有所增加，但要遠小于單層纏繞時作用在滾筒筒身徑向壓力的疊加值。一方面，這是由于第n層連續油管纏入滾筒后，第n-1層連續油管因受到第n層連續油管的擠壓而變形；另一方面，隨著連續油管層數的增加，第n層油管纏繞時所要克服的筒身剛度增大，滾筒筒身的變形幅度較第n-1層纏繞時逐漸減小。

3 連續油管滾筒有限元分析

3.1 有限元建模及網格劃分

在進行滾筒有限元建模時，為了簡化計算并減少計算結果的奇異性，需對模型進行一定處理(如忽略細小倒角特征、略去非主要承載構件等)，并作如下假設：

1) 滾筒焊接牢固無缺陷，且焊接強度足夠。

2) 不考慮連續油管與滾筒之間、滾筒軸與安裝軸承之間的摩擦。

3) 連續油管滾筒整體受力均勻，滾筒所受徑向壓力及滾筒輻板所受軸向力平均分布在滾筒筒身及輻板上。

網格劃分采用殼單元、實體單元混合方式，單元數量合計161 893個，殼單元與實體單元連接處均采用MPC算法以減少因實體單元與殼單元自由度不匹配而導致的結果異常。

3.2 邊界及載荷施加

1) 滾筒軸一端建立固定鉸接約束，另一端建立旋轉鉸接約束。

2) 將表2中第2層、第5層、第7層、第10層、第12層、第15層連續油管纏入后的計算結果定義為6種計算工況(a、b、c、d、e、f)，同時考慮不同纏繞層數下的連續油管重力，且均勻作用于滾筒筒身上。

3) 滾筒輻板左右兩側均需施加軸向力，且二者等大反向。

3.3 計算結果

根據API、DNV及我司設備應用情況，綜合選取滾筒安全系數為1.67，對應的滾筒許用應力約為207 MPa。為了后文仿真與試驗結果的對比，分別截取滾筒等效應力及Y向正應變結果如圖5～6所示。

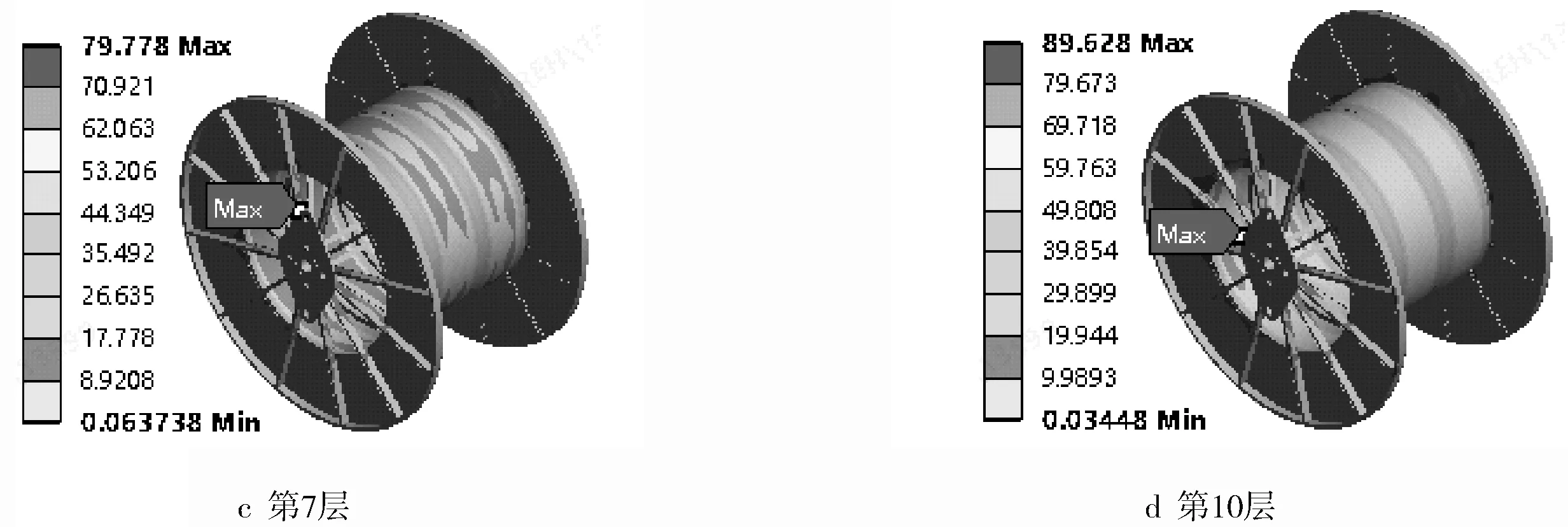
圖5 連續油管滾筒等效應力云圖

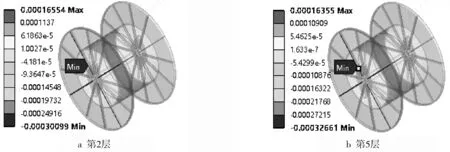
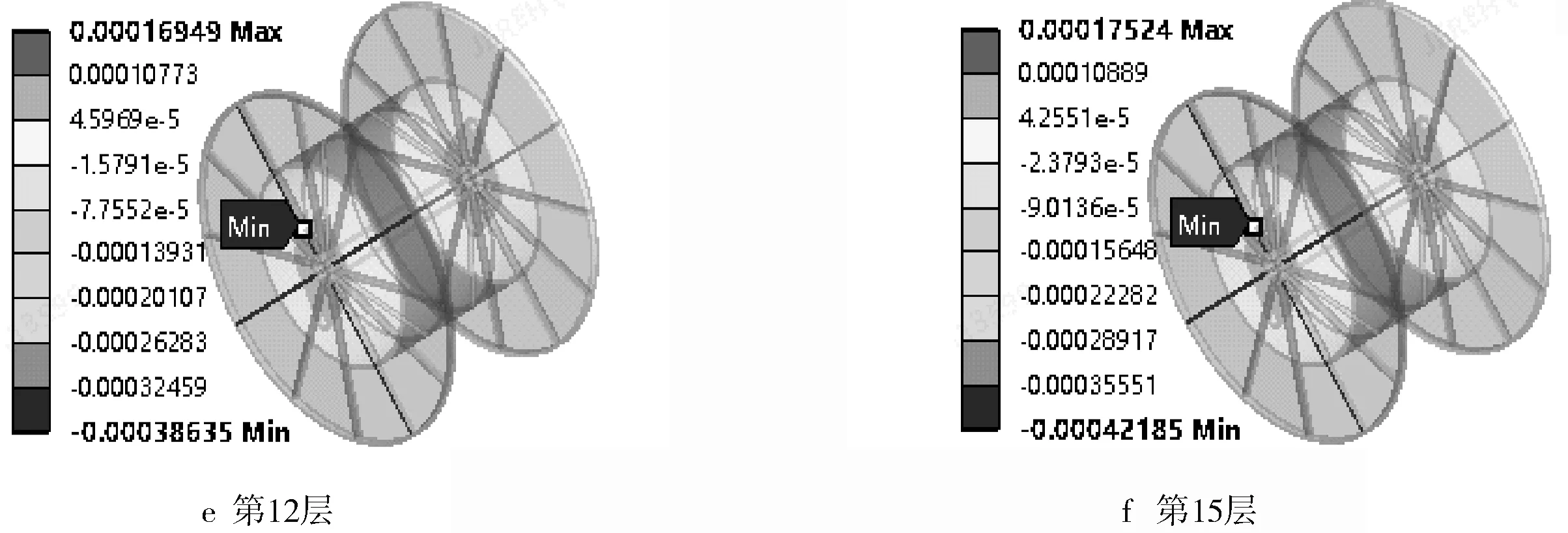
圖6 連續油管滾筒正應變云圖

由圖5～6可以看出，在上述載荷作用下，該滾筒等效應力均小于許用應力，強度滿足要求。隨著纏繞層數及施加載荷的增大，滾筒等效應力及正應變均增大。

4 滾筒應力-應變試驗及結果分析

為了驗證連續油管滾筒多層纏繞下徑向及軸向力計算方法的有效性，對上述滾筒進行應力-應變試驗。試驗工況分為纏管工況及倒管工況，其中纏管工況主要采集連續油管制造完成纏入運輸滾筒過程的應變值，倒管工況主要采集連續油管作業過程中由運輸滾筒倒入作業滾筒過程的應變值。與仿真工況一致，分別記錄連續油管纏入2層、5層、7層、10層、12層、15層時滾筒應變數值作為對比數據，且每種工況分別測試2組數據以保證測量結果的準確性。

4.1 纏管工況

將連續油管滾筒近似為左右對稱結構，設置單側應力-應變測點4個，每個測點處分別布置1個周向應變片和軸向應變片。

為了保證應變測量的準確性，粘貼應變片之前需將測點打磨平整，粘貼完成后需將導線固定牢固，防止滾筒旋轉過程中的脫落，應變片布置位置示意圖及現場測試情況如圖7～8所示。

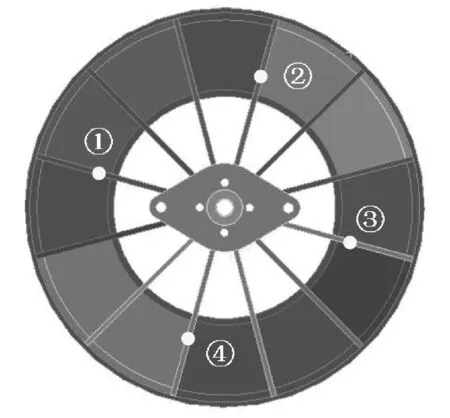
圖7 連續油管滾筒應力-應變測點布置位置

圖8 連續油管滾筒應力-應變試驗現場(纏管工況)

纏管6種工況下各測點應變的測量數據如表3所示。

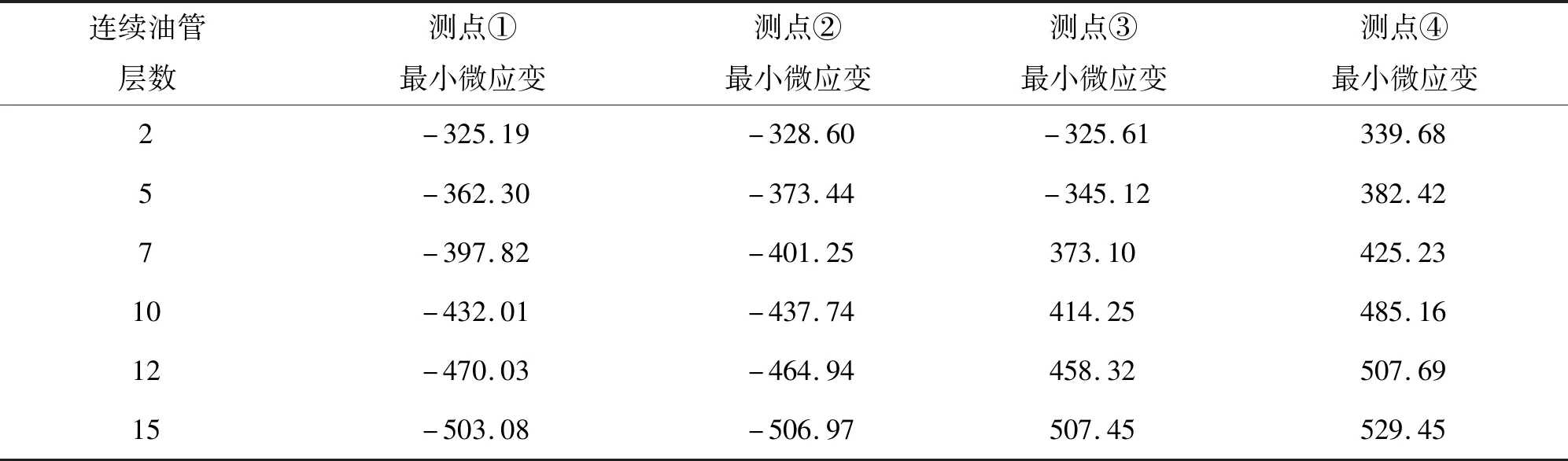
表3 連續油管滾筒應變測試數據(纏管工況)

從測試數據可以看出，由于滾筒輻板受到油管軸向壓力，應變結果為負值。隨著連續油管層數的增加，應變數值也逐漸變大，其主要原因在于油管層數增加導致作用于輻板上的軸向力增加。另外，由于輻板為懸臂結構，當連續油管層數增加后，軸向力對測點的力臂也增大，進一步導致測點應變的增大，故在設計滾筒時，須進行輻板的強度校核。

將表3中的應變試驗結果與仿真結果進行對比如圖9所示。

從圖9可以看出，應變試驗結果與理論計算結果變化趨勢相近，但是試驗結果大于理論值，這主要是因為纏管工況中連續油管松弛角度小于理論計算中的40°，進而導致連續油管對滾筒輻板的軸向力增大。

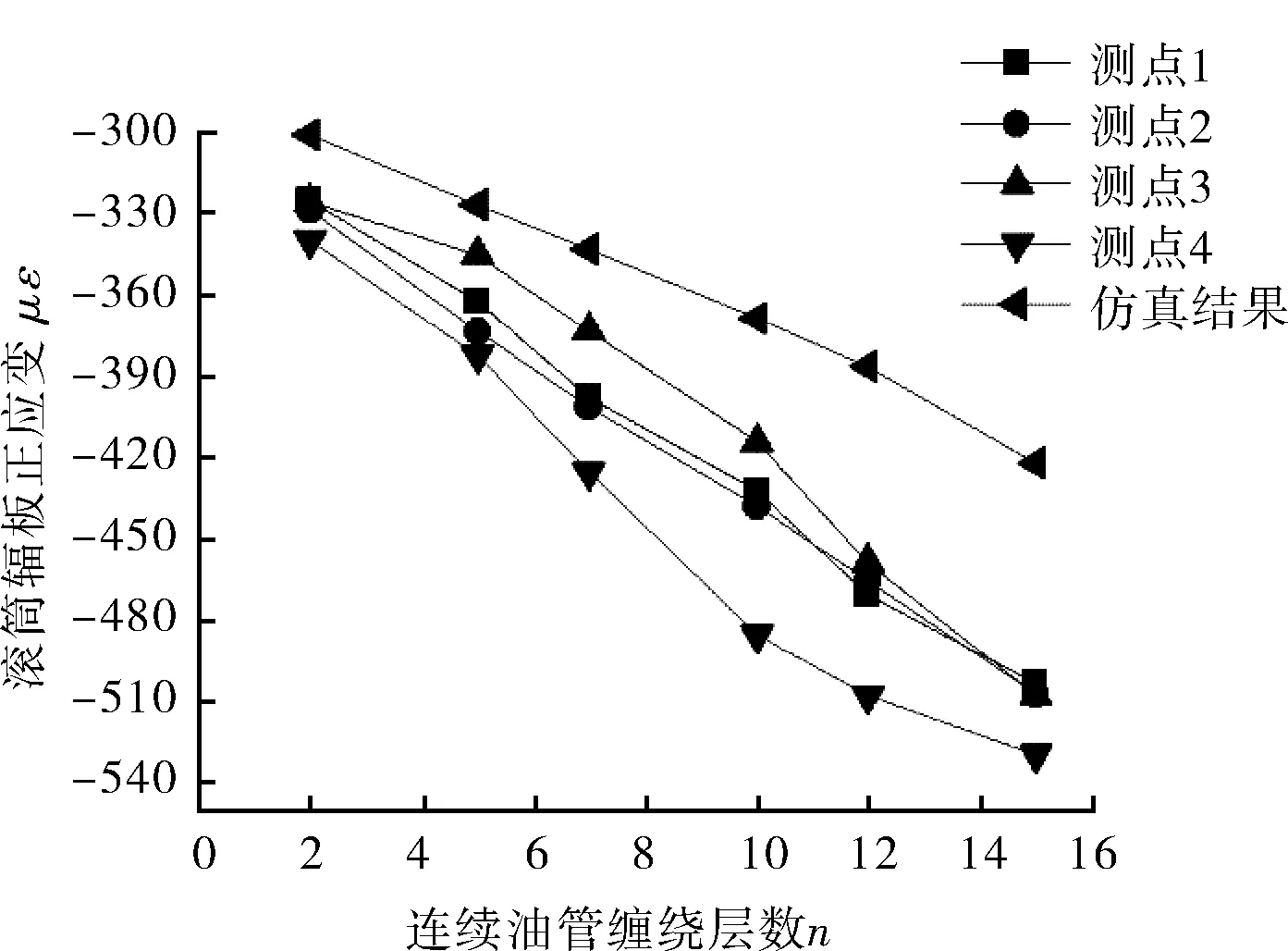
圖9 應變仿真與試驗結果對比(纏管工況)

4.2 倒管工況

倒管工況中應變片布置與纏管工況一致，此處不再贅述，現場測試情況如圖10所示。

圖10 連續油管滾筒應力-應變試驗現場(倒管工況)

倒管工況各測點應變的測量數據如表4所示，倒管工況試驗結果與仿真結果進行對比如圖11所示。

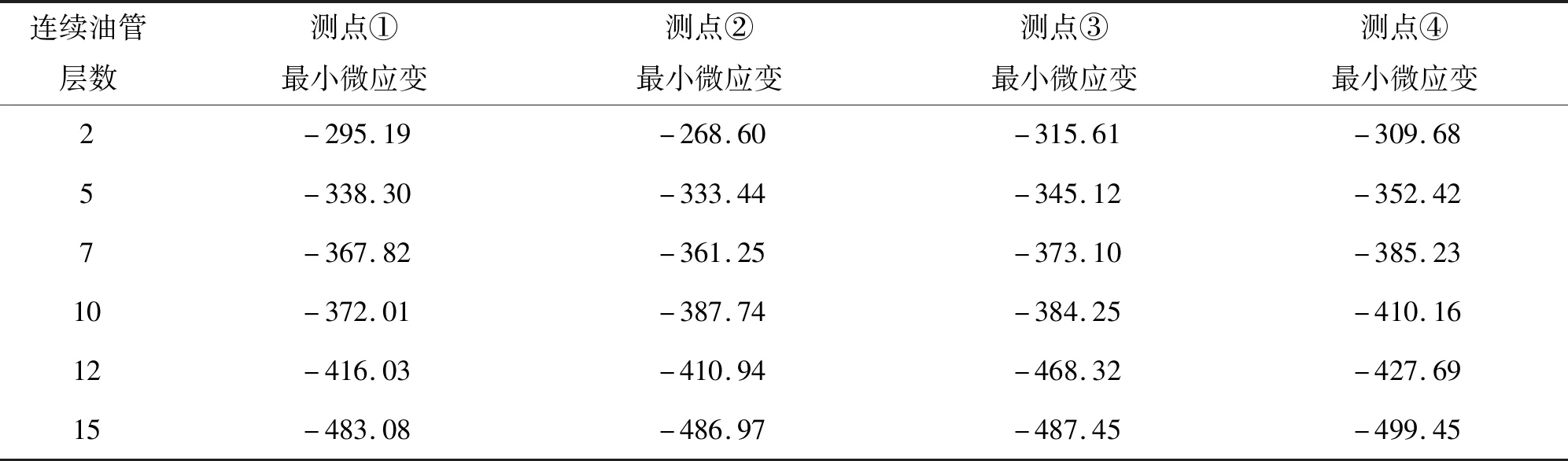
表4 連續油管滾筒應變測試數據(倒管工況)

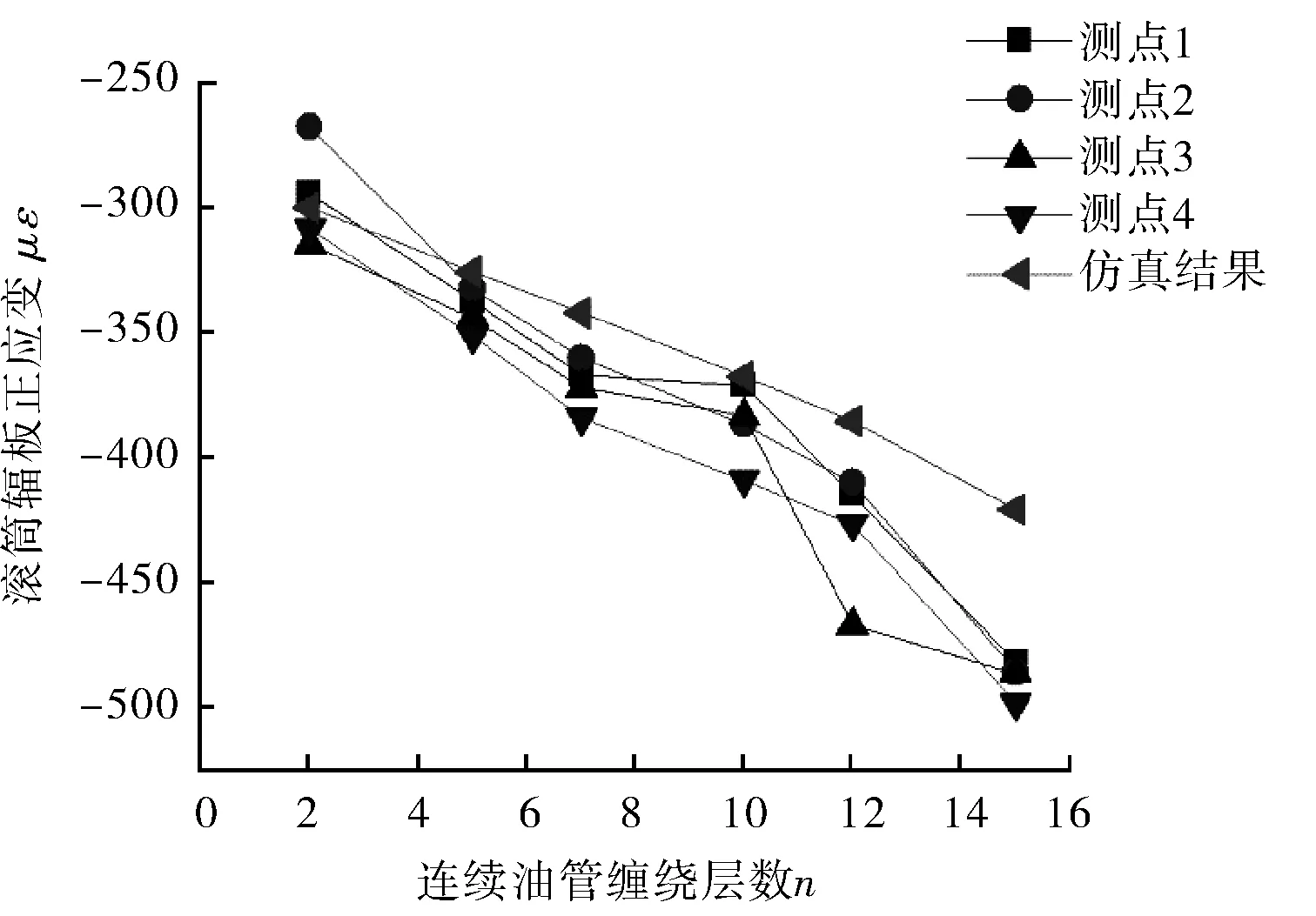
圖11 應變仿真與試驗結果對比(倒管工況)

從圖11可以看出，應變試驗結果與理論計算結果總體上趨于一致，試驗結果略小于理論值，但是相較于纏管工況，倒管工況應變測試結果與理論計算結果的一致性更高。

綜合理論分析及試驗得到的結果，發現隨著連續油管層數的增加，連續油管滾筒筒身所受徑向力、滾筒輻板所受軸向力逐漸增大，在進行滾筒設計時應充分考慮二者對滾筒強度的影響。另外，通過上述分析不難發現，多層纏繞系數λ1、λ2隨連續油管層數而增大，但是連續油管超過10層以后λ1增長幅度逐漸減小，且λ2與纏繞層數n之間可擬合出近似的線性關系，即

λ2=0.608 1n+0.289 1

(18)

因此從工程設計校核效率上考慮，在滾筒設計初期，可以將第1層連續油管纏入時滾筒所受徑向壓力乘以安全系數作為多層纏繞滾筒受到的徑向壓力的近似值。同樣地，在滾筒設計初期，可通過式(18)計算出λ2，然后將第1層連續油管纏入時滾筒輻板所受軸向力乘以λ2再乘以安全系數作為多層纏繞滾筒輻板受到的軸向力的近似值。

5 結論

1) 通過連續油管滾筒單層及多層纏管受力分析及理論計算發現，多層連續油管纏繞相較于單層連續油管纏繞，滾筒筒身所受徑向壓力有所增加，但要遠小于單層纏繞時作用在滾筒筒身徑向壓力的疊加值。

2) 在多層連續油管纏繞下，纏管工況、倒管工況應變測試值與理論值的對比結果表明，理論計算結果與測試結果總體趨于一致，從而驗證了理論計算的合理性。

3) 滾筒所受徑向壓力對于纏繞層數變化的敏感度較小，不同纏繞層數對滾筒輻板軸向力的影響較大，因此從工程設計校核效率上考慮，在滾筒設計初期，可以通過簡化計算方式，得到多層纏繞滾筒受到徑向壓力及軸向力的近似值。