需求信息不對稱下數據交易拍賣定價機制研究

郭鑫鑫, 李倩茹, 王海燕, 杜建國

(1.江蘇大學 管理學院,江蘇 鎮江 212013; 2.江蘇科技大學 經濟管理學院,江蘇 鎮江 212100; 3.東南大學 經濟管理學院,江蘇 南京 211189)

0 引言

伴隨著機器學習和數據挖掘技術等迅速發展,數據已成為數字經濟時代重要的生產要素和戰略資產[1]。然而,數據產品的定價受多種主客觀因素影響,呈現出價值多樣性、不確定性等特征,難以按照傳統商品的方式進行定價[2]。從數據賣方角度,同一數據產品可以多次出售,使其不能按照交易價格等于邊際成本進行定價;從數據買方角度,數據產品只有在使用后才能明確其真實的價值,具有一定的價值滯后性[3]。面對數據產品定價過程中缺乏歷史經驗數據進行借鑒,探究數據產品交易定價機制成為推動數據交易平臺可持續發展的關鍵[4,5]。

從實際數據交易場景出發,參與數據產品交易雙方(即數據交易平臺和潛在數據需求者)往往存在著需求信息不對稱。一方面,數據交易平臺不能準確預測數據需求者的期望交易價格、購買能力及風險偏好等信息,傾向設計較高的交易價格來銷售數據產品;另一方面,數據需求者不能事前準確獲知被交易數據產品的質量、完整性和真實性等信息,傾向選擇以不超過對其估值的價格來購買數據產品[6]。眾所周知,數據交易雙方追求自身收益最大化,均不會主動披露自身對數據產品的認知信息。此外,數據需求者對數據產品的期望效用也存在不同認知,致使對數據產品呈現出差異化的需求[7,8]。

當前,相關學者已從不同的視角出發對數據交易定價進行了研究。BIMPIKIS等[9]研究了壟斷市場環境下數據使用者之間的競爭如何影響數據經紀商的最優銷售策略。RAY等[10]在數據交易過程中引入樣品展示來緩解雙方間信息不對稱,通過構建數據交易協商式定價模型,探討經紀商是否應該以及如何進行樣品展示。喻海飛和黃晉婷[11]研究了閉環數據供應鏈下的數據產品定價策略問題,分別構建了集中定價、分散定價和收益共享三種不同的數據定價模型。馬滔等[12]構建了數據披露與數據交易兩階段博弈模型,探究數據擁有者的價格披露與數據經紀商交易價格間交互關系。此外,拍賣定價方法也被部分學者應用于數據產品交易定價中。通過梳理相關文獻發現,學者們采用的拍賣模型涉及維克里拍賣、VCG拍賣、反向拍賣和雙向拍賣等類型。在數據交易過程中,具體選擇何種拍賣機制需要綜合考量買賣雙方的相對市場力量,是否有中介機構充當拍賣商及設定的定價原則等因素。張小偉等[13]對采用博弈論和拍賣研究方法的相關文獻進行了綜述,比較了兩種研究方法下的不同數據定價模型及模型的優劣勢。

上述文獻為本文設計數據產品交易拍賣定價機制奠定了研究基礎,但尚未發現相關文獻針對數據交易價格和交易量聯合決策問題開展探究。基于機制設計理論和多物品最優拍賣設計原理[14],本文以排他性強的數據產品為研究對象,探究數據交易平臺與數據需求者進行數據所有權交易,通過設計拍賣機制來確定最優的數據產品交易價格及相應的交易數量。

1 模型假設和問題描述

1.1 模型假設

根據實際的交易場景,考慮數據交易市場中存在一個數據交易平臺和眾多潛在數據需求者。每位數據需求者依據數據產品價格大小決策數據購買量,故整個數據交易過程呈現“一對多”的博弈關系。為方便后文的問題描述和模型分析進行如下假設。

1)假設市場上數據需求者的數量為n,即i=1,2,…,n,這些數據需求者構成的集合為N={1,2,…,n}。數據交易平臺向數據需求者設定的初始交易價格為p,相應的數據需求者i=1,2,…,n的數據需求量為xi≥0,i∈N,xi=0,其中,i=1,2,…,n表示數據需求者選擇放棄購買。

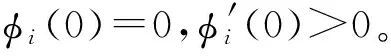
3)依據數據交易平臺的歷史成本信息,定義c(·)為數據交易平臺對數據產品進行脫敏、清洗及格式化等處理的成本函數,并且是關于數據量xi,i∈N連續單調遞增可微的凸函數[15]。

4)定義ki為數據需求者i=1,2,…,n的最大數據需求量,D是數據交易平臺可供給的總數據量。為保證優化問題存在最優解,假設D與ki滿足如下關系:

基于前面的相關符號定義,可以獲知數據需求者i=1,2,…,n從平臺上購買數據產品時,其獲得的收益為

vi(xi)=φi(xi)-pxi

(1)

考慮到數據需求者追求自身收益最大化,將依據平臺設定的交易價格決策數據購買量,故數據需求者面臨的決策問題為

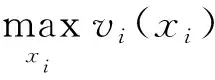
(2)

(3)

同理,基于上文給出相關符號定義,數據交易平臺的收益函數可表示為

(4)

1.2 問題描述

本文聚焦于數據交易平臺與數據需求者進行數據所有權交易,即部分數據產品被交易給某位需求者后,無法再交易給其他需求者,呈現出排他性。因此,在數據供給量固定的情況下,數據交易平臺傾向于設計較高的價格,以實現平臺收益最大化。然而,當平臺設定較高的交易價格時,數據需求者對數據產品的偏好降低,進而影響數據產品的需求量[16]。考慮到數據交易平臺與數據需求者間存在利益沖突及數據需求者相互之間的競爭關系,數據交易平臺需要設計一個公平合理的交易價格,通過對數據交易量合理分配,使得在滿足數據需求者的需求時,實現平臺自身收益最大化,即實現數據交易系統社會福利最大化。根據數據交易系統的社會福利為數據交易平臺收益及所有數據需求者的收益之和,可得

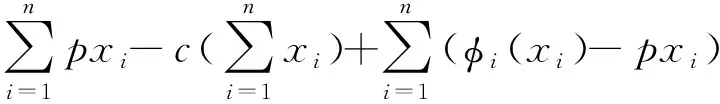
(5)

進一步,數據交易平臺面臨的決策問題可表示為

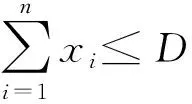
(6)

顯然,數據交易平臺與數據需求者間存在需求信息不對稱,導致平臺不能獲知φi(·)的具體表達式,進而無法對所構建的優化問題(6)進行求解,換句話說,優化問題(6)是一個NP-hard問題。

基于最優化理論,數據交易平臺要獲得優化問題(6)的最優解,需要數據需求者主動共享自身的效用函數信息。然而,考慮數據需求者的自私性,往往會策略性地共享自身的效用函數信息,以追求自身收益的最大化。因此,要解決這種信息不對稱下的優化問題,本文利用機制設計理論和拍賣理論來設計一種數據交易拍賣定價機制,引導數據需求者提交真實的效用函數信息,進而決策出最優的數據產品交易價格及相應的交易量。

2 機制設計環境描述與目標設定

2.1 數據交易定價機制環境描述

假設數據需求者對數據產品的偏好為θi,i∈N,其代表著數據需求者的類型[17]。定義數據需求者向數據交易平臺進行投標策略為si:Θi→Si,其中,Θi是數據需求者i=1,2,…,n的類型空間,Si為基于數據需求者類型的策略空間。每位數據需求者通過要向平臺進行投標,以揭示自身的偏好信息。在獲得數據需求者的投標后,數據交易平臺可以計算出最優的數據產品交易價格和交易量,即結果函數g(·)。因此,數據交易平臺要設計的拍賣定價機制為M=(S1,S2,…,Sn,g(·)),其中包含信息空間S=S1×S2×…×Sn和結果函數g=S1×S2×…×Sn→X×P。該結果函數可將數據需求者的投標策略映射為具體的交易結果,即g(S)=(x1,…,xn,p)。

2.2 數據交易定價機制目標設定

假設數據需求者相互獨立且具有不完全信息,投標過程中采用的是貝葉斯博弈。在選擇投標策略時,每位數據需求者始終選擇能夠最大化自身收益的投標策略,并且不考慮其他數據需求者的行動策略。因此,本文采用占優策略均衡來描述數據需求者間的博弈均衡結果。

3 數據交易拍賣定價機制設計

3.1 模型處理

借鑒相關文獻中提出的研究方法,本文對優化問題(6)中的約束條件進行放松,將不完全信息下的Stackelberg博弈問題轉化成資源分配問題,即

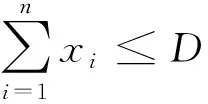
(7)

顯然,在優化問題(7)中,數據交易平臺的決策變量轉變為數據需求者的交易數量xi,i∈N。因此,本文將優化問題(7)看作數據交易平臺與數據需求者進行合作來實現數據交易系統社會福利最大化。顯然,優化問題(7)的最優解是優化問題(6)最優解的上界。換句話說,通過優化問題(7)實現的數據交易系統社會福利往往大于通過優化問題(6)實現的數據交易系統社會福利。此外,由于c(·)是連續遞增可微的凸函數,而φi(·)是連續遞增可微的凹函數,使得優化問題(7)的最優解可以通過設定恰當的數據交易價格來實現,表明通過優化問題(7)獲得的最優解是緊湊的。因此,通過數據交易拍賣定價機制M=(S1,…,Sn,g(·))獲得的數據交易分配結果只需滿足優化問題(7)即可。

3.2 設計數據交易拍賣定價機制

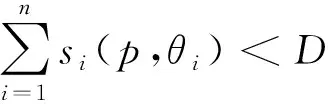
由數據需求者效用函數(2)關于xi進行一階求導,可得

(8)

同時,將優化問題(6)關于數據交易價格p應用KKT條件,可得,

(9)

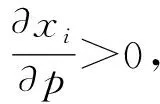
(10)

進一步,整合公式(8)和公式(10),可得

(11)

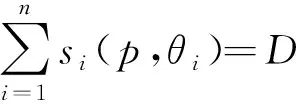
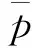
命題1數據交易平臺的拍賣定價機制為M*=(S1,…,Sn,g(·)),信息空間Si是關于數據交易價格p連續單調遞減的函數空間,結果函數g(·)為

g(s1(·,θ1),…,sn(·,θn))=(s1(p*,θ1),…,sn(p*,θn),p*)

(12)

其中,p*是數據產品最優交易價格且滿足

(13)

(14)

(15)

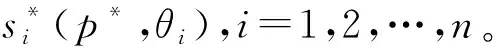
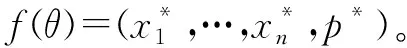
4 算例實驗

通過一個算例來驗證所設計的數據交易拍賣定價機制的有效性和合理性。借鑒采用需求函數進行投標的相關文獻,將數據需求者向數據交易平臺提交的投標策略設為

si(p,θi)=ki-pθi,?i=1,2,…,n

(16)

顯然,該投標策略表示數據需求者i=1,2,…,n的最大數據需求量為ki,i∈N;伴隨著數據交易價格p越高,數據需求者對數據產品的需求量越少;反之,數據需求者對數據產品的需求量越多,符合現實中的數據產品交易場景。

根據前文的設定,si(p,θi)滿足

si(p,θi)≥0

(17)

進一步,經過計算可知數據需求者的偏好θi的取值范圍為

(18)

另外,數據需求者i=1,2,…,n的收益函數可表示為

ui(p,θi)=φi(si(p,θi))-p×si(p,θi)

(19)

因此,數據需求者i=1,2,…,n面臨的決策問題為

(20)

為了便于下文計算,本文設定數據產品供給總量是固定的而非彈性變化,故數據交易系統社會福利最大化等價于最大化所有數據需求者的效用,即

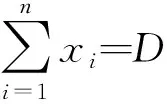
(21)

根據前文設計的數據交易拍賣定價機制,數據交易平臺按照數據需求者提交的需求函數對數據產品交易量進行分配。因此,要實現數據交易市場出清,需要滿足

(22)

經過計算可得,數據產品最優交易價格為

(23)

綜上,數據交易平臺可以設定最優數據交易價格為(23),分配給數據需求者i=1,2,…,n的交易量為si(p*,θi)。

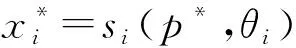
5 結束語

從信息不對稱角度出發,數據交易平臺無法獲知數據需求者的效用函數信息,進而無法設定最優的數據交易價格及合理分配數據交易量。本文聚焦于數據交易平臺與數據需求者進行數據所有權交易,利用機制設計理論和拍賣理論,將數據交易定價問題映射為機制設計問題。通過對數據交易平臺與數據需求者間交易行為分析,設計了數據產品交易拍賣定價機制,其中信息空間是關于數據交易價格連續單調遞減的函數空間,結果函數是由數據需求者提交的需求函數決定。所設計的數據交易拍賣定價機制可激勵數據需求者投標真實的需求函數信息,滿足拍賣理論中的激勵兼容和個體理性。從實踐應用角度,本文提出的研究方法可有效地解決需求信息不完全下的數據產品交易定價問題,減少數據交易平臺與數據需求者的討價還價行為,為數據交易平臺設計公平的交易價格及合理分配數據交易量提供了理論與實踐指導。

本文研究過程中仍存在一些不足如尚未對提供撮合服務的數據交易平臺的定價機制進行分析、探究排他性較弱的數據產品的定價機制等。學者們未來可以進一步挖掘數據交易定價與交易量分配聯合決策問題,開展更深入和更廣泛的研究,以期完善本文所提出的拍賣定價機制。