UHPC-T梁抗彎性能試驗(yàn)研究與理論計(jì)算

朱 琦，葉力豪，蔡 瑋，謝 文

(寧波大學(xué)土木工程與地理環(huán)境學(xué)院，浙江寧波 315211)

0 引 言

超高性能混凝土(Ultra-high Performance Concrete，UHPC)是一種具有超高抗壓、抗拉強(qiáng)度和高韌性、高耐久性的新型水泥基復(fù)合材料，將其應(yīng)用于橋梁結(jié)構(gòu)中，可減輕結(jié)構(gòu)自重，提高承載力和耐久性，具有廣闊的應(yīng)用前景[1-6]。盡管目前中國尚未制定UHPC橋梁設(shè)計(jì)規(guī)范，但不少學(xué)者已進(jìn)行了較深入的研究。鄧宗才等[7]研究表明：截面形式對(duì)UHPC梁的開裂荷載與延性影響甚大。傅元方[8]試驗(yàn)研究表明：UHPC梁的屈服和極限荷載受縱向配筋率的影響較大。孫小凱等[9]通過四點(diǎn)彎曲試驗(yàn)研究發(fā)現(xiàn)：縱筋配筋率不影響UHPC梁的開裂彎矩，但對(duì)其極限承載力的影響顯著。Yang等[10]研究了配筋率和鋼纖維體積摻量對(duì)梁受力性能的影響，結(jié)果表明：當(dāng)鋼纖維體積摻量不變時(shí)，縱向配筋率對(duì)UHPC梁的開裂性能無影響，對(duì)UHPC梁的極限承載力以及延性均有顯著影響。Turker等[11]研究發(fā)現(xiàn)：當(dāng)鋼纖維體積摻量一定時(shí)，配筋率越大，UHPC梁的極限承載力越大，延性也更強(qiáng)，但超過一定配筋率時(shí)，對(duì)延性性能的改善作用減弱。梁興文等[12]研究發(fā)現(xiàn)：縱向配筋率對(duì)UHPC梁的開裂荷載影響不大，但縱向配筋率可大幅提升UHPC梁的屈服荷載和極限荷載。彭飛等[13]考慮了鋼纖維對(duì)UHPC受拉區(qū)的抗彎貢獻(xiàn)，結(jié)果表明：鋼纖維長度也是影響受拉區(qū)UHPC抗彎貢獻(xiàn)的主要參數(shù)。曹霞等[14]開展了6根高強(qiáng)鋼筋UHPC梁抗彎試驗(yàn)，研究了不同配筋率、縱筋等級(jí)、縱筋直徑和受壓鋼筋直徑對(duì)UHPC受力性能的影響規(guī)律。林明暢[15]設(shè)計(jì)制作了6組18根不同配筋率UHPC試驗(yàn)梁，探索了UHPC梁的適筋、超筋和少筋的破壞形態(tài)以及裂縫發(fā)展?fàn)顟B(tài)，推導(dǎo)了UHPC梁的開裂彎矩、極限彎矩和抗彎剛度計(jì)算公式。徐海賓等[16]在現(xiàn)行規(guī)范公式的基礎(chǔ)上引入抗裂影響系數(shù)和裂縫修正系數(shù)，給出了UHPC梁的開裂彎矩和最大裂縫寬度計(jì)算公式。劉超等[17]在平截面假定基礎(chǔ)上推導(dǎo)了配筋高應(yīng)變強(qiáng)化的UHPC-T梁抗彎承載力計(jì)算公式，并與國外提出的計(jì)算方法進(jìn)行對(duì)比，結(jié)果表明，所提出方法的計(jì)算值與試驗(yàn)值吻合度較高。李立峰等[18]進(jìn)行了大比例預(yù)應(yīng)力UHPC-T梁抗彎試驗(yàn)，改進(jìn)了開裂荷載和極限荷載計(jì)算方法。徐海賓等[19]試驗(yàn)研究了6根預(yù)應(yīng)力UHPC-T梁的抗彎性能，引入纖維長度修正系數(shù)和抗裂影響系數(shù)，對(duì)截面抵抗矩塑性影響系數(shù)進(jìn)行修正，得到了預(yù)應(yīng)力UHPC-T梁的開裂彎矩計(jì)算公式。

綜上所述，目前的研究主要以矩形截面為主探討UHPC梁的力學(xué)性能，而以預(yù)應(yīng)力為主要影響因素研究其對(duì)T形截面抗彎性能的影響相對(duì)較少。本文以橋梁工程中的T梁為研究對(duì)象，制作4根UHPC-T梁(包括1根預(yù)應(yīng)力UHPC-T梁)和1根普通混凝土T梁(對(duì)照梁)，研究配筋率和預(yù)應(yīng)力對(duì)UHPC-T梁抗彎性能的影響；最后采用理論公式計(jì)算UHPC-T梁的開裂彎矩和極限彎矩等關(guān)鍵性能參數(shù)。

1 試驗(yàn)概況

1.1 模型制作及加載測點(diǎn)布置

由于受經(jīng)費(fèi)和試驗(yàn)場地等條件限制，足尺模型試驗(yàn)難以實(shí)現(xiàn)，因此采用縮尺模型開展相關(guān)研究工作。結(jié)合自身試驗(yàn)條件和研究目的，縮尺模型參照并改造了文獻(xiàn)[20]中的試驗(yàn)?zāi)Ｐ停凑{(diào)整了模型截面翼緣和腹板尺寸，但試驗(yàn)?zāi)Ｐ土旱目箯澓涂辜舻刃阅芫鶟M足設(shè)計(jì)規(guī)范要求。UHPC-T梁的設(shè)計(jì)長度為2 400 mm，為防止兩端發(fā)生錨固破壞，加載時(shí)兩邊預(yù)留了150 mm，計(jì)算跨度為2 100 mm，如圖1(a)所示；T形截面的腹板尺寸為120 mm×150 mm，翼緣尺寸為280 mm×100 mm，如圖1(b)所示。預(yù)應(yīng)力UHPC-T梁的預(yù)應(yīng)力采用后張法施加，在距梁底下緣56 mm處布置1根直徑15.2 mm的預(yù)應(yīng)力鋼鉸線，如圖1(c)所示；其中錨墊板采用10 mm厚鋼板以防止錨固區(qū)局部壓碎，張拉預(yù)應(yīng)力為110 kN。試驗(yàn)T梁的具體分組見表1，試驗(yàn)主要考慮配筋率和預(yù)應(yīng)力等影響，其中普通混凝土T梁為對(duì)照梁。

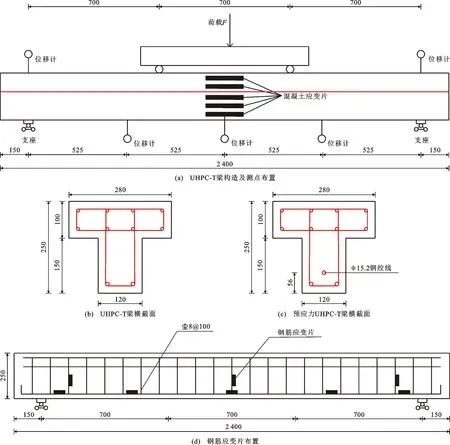
表1 T梁試驗(yàn)分組Table 1 T-beam test group

UHPC-T梁的制作采用常規(guī)的施工工藝，即先支模、綁扎鋼筋、后澆筑UHPC和自然條件養(yǎng)護(hù)，現(xiàn)場作業(yè)如圖2所示；試驗(yàn)采用的UHPC中水泥、硅粉、石英砂、水膠比的配合比為1∶0.5∶1.5∶0.18，且添加了2%的減水劑和體積摻量為2%的鋼纖維。

自然條件下養(yǎng)護(hù)28 d達(dá)到齡期后，采用三等分點(diǎn)進(jìn)行抗彎加載試驗(yàn)(圖3)，通過分配梁將荷載對(duì)稱分配到梁的兩個(gè)三分點(diǎn)處，中間為純彎段。試驗(yàn)加載儀器為結(jié)構(gòu)疲勞試驗(yàn)系統(tǒng)PWS-250，試驗(yàn)開 始前先預(yù)加載，如無異常，則卸載到0 kN再開始正式加載。試驗(yàn)加載采用分級(jí)加載，在達(dá)到使用狀態(tài)試驗(yàn)荷載值Fs之前，每級(jí)加載值不超過0.10Fs，接近開裂荷載時(shí)，每級(jí)加載值不超過0.05Fs。開裂后每級(jí)加載控制為10 kN，UHPC-T梁到80 kN后改用位移1 mm·min-1控制加載直至梁破壞；普通混凝土梁到20 kN后改用位移1 mm·min-1加載直至梁破壞。

測試內(nèi)容包括：豎向位移、混凝土應(yīng)變、鋼筋應(yīng)變、裂縫等。①位移測試：沿梁安裝5個(gè)豎向位移計(jì)(含兩端支座處位移計(jì))，如圖1(a)所示。②應(yīng)變測試：布置鋼筋應(yīng)變片用于測試箍筋和縱筋應(yīng)變，如圖1(d)所示；在梁跨中沿梁高布置5個(gè)混凝土應(yīng)變片測試混凝土應(yīng)變沿梁高的分布規(guī)律，如圖1(a)所示。③裂縫測試：利用裂縫觀測儀測量每個(gè)荷載步下最大裂縫寬度，并利用記號(hào)筆標(biāo)記裂縫發(fā)展情況。

1.2 材料力學(xué)性能

1.2.1 UHPC力學(xué)性能

澆筑UHPC試驗(yàn)簡支梁時(shí)，同時(shí)制作了3個(gè)邊長為100 mm的立方體試件以測試其抗壓強(qiáng)度，制備了3個(gè)100 mm×100 mm×300 mm長方體試件用于測試其彈性模量。澆筑了3個(gè)100 mm×100 mm×400 mm長方體試件以測試其抗彎折強(qiáng)度，加載裝置見圖4(a)；加工了3個(gè)180 mm×25 mm×25 mm狗骨形試件用于測試軸心抗拉強(qiáng)度，測試裝置見圖4(b)。所有試件與UHPC試驗(yàn)簡支梁的養(yǎng)護(hù)條件相同，測得的力學(xué)性能如表2所示。

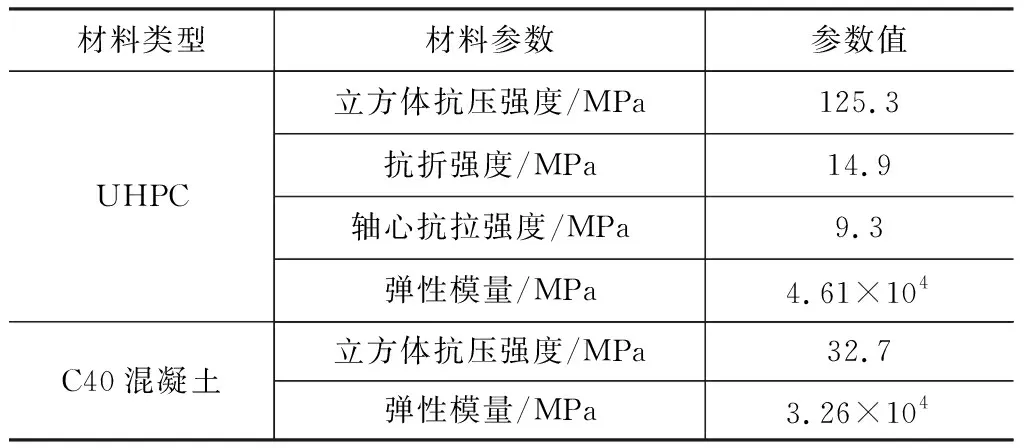
表2 UHPC與C40混凝土力學(xué)性能Table 2 Mechanical properties of UHPC and C40 concrete

1.2.2 鋼筋力學(xué)性能

按照《金屬材料 室溫拉伸試驗(yàn)方法》[21]規(guī)定進(jìn)行鋼筋拉伸試驗(yàn)。所得的鋼筋物理力學(xué)性能指標(biāo)如屈服強(qiáng)度、極限強(qiáng)度等見表3。

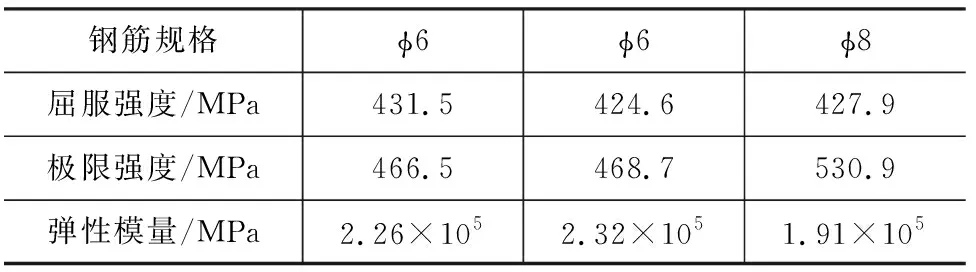
表3 鋼筋力學(xué)性能Table 3 Mechanical properties of reinforced rebars

2 配筋率對(duì)UHPC-T梁抗彎性能的影響

2.1 裂縫分布與抗裂性能

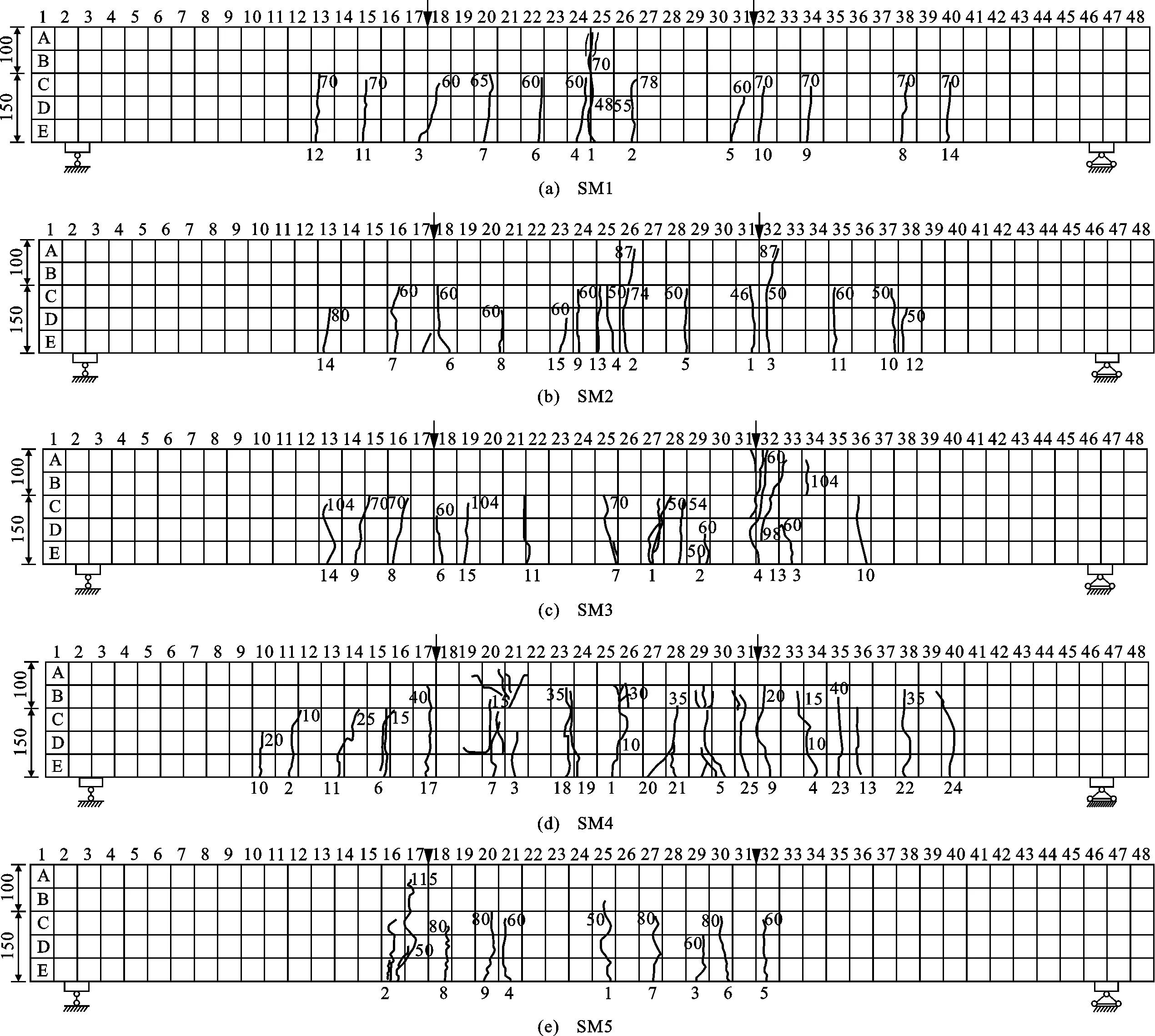
各模型梁的裂縫分布如圖5所示，其中裂縫中數(shù)字為裂縫發(fā)展位置對(duì)應(yīng)的荷載，單位為kN。由圖5可以看出，各試驗(yàn)梁裂縫分布有如下特點(diǎn)：①相比SM4梁，SM1、SM2、SM3梁的裂縫出現(xiàn)較晚，且發(fā)展速度較慢；②SM1、SM2、SM3梁翼緣上裂縫較少，主要集中在加載點(diǎn)附近，而SM4梁翼緣上有較多裂縫且穿過翼緣向上發(fā)展；③SM1、SM2、SM3梁裂縫數(shù)量遠(yuǎn)小于SM4梁，表明鋼纖維可阻礙裂縫發(fā)展，使裂縫分布更加均勻。從圖5還可看出，SM1、SM2、SM3梁的裂縫發(fā)展特征為：隨著荷載的增加，裂縫寬度逐漸變大，裂縫不斷向上擴(kuò)展；當(dāng)荷載持續(xù)增加時(shí)，梁的裂縫數(shù)量和寬度逐漸增大，并能聽到受拉區(qū)混凝土內(nèi)鋼纖維被拔出的聲音，但直到試驗(yàn)由于破壞而停止，其受壓區(qū)混凝土未被壓碎。

裂縫對(duì)結(jié)構(gòu)的剛度和耐久性產(chǎn)生顯著影響，圖6給出了各模型梁的荷載與最大裂縫寬度關(guān)系。與SM3梁相比，SM1、SM2梁由于其配筋率較低，初裂過后它對(duì)裂縫寬度的限制作用有限，導(dǎo)致開裂過后裂縫發(fā)展迅速，比如SM1、SM2、SM3梁的開裂荷載對(duì)應(yīng)的最大裂縫寬度均為0.01 mm，而加載至80 kN時(shí)對(duì)應(yīng)的最大裂縫寬度分別為0.22、0.26、0.08 mm，表明提高配筋率可阻止UHPC-T梁裂縫的發(fā)展。當(dāng)配筋率從0.209%提高至0.744%，SM1梁和SM3梁極限荷載對(duì)應(yīng)的最大裂縫寬度從1.92 mm降至1.56 mm，表明提高配筋率可以增大梁的抗裂性能和安全性能。SM2梁和SM4梁最大裂縫寬度均為0.01 mm時(shí)，對(duì)應(yīng)的開裂荷載分別為46 kN和10 kN，當(dāng)SM4梁加載至20 kN時(shí)，其最大裂縫寬度已擴(kuò)大至0.18 mm，表明UHPC可阻止T梁裂縫的發(fā)展和提升梁的抗裂性能和承載能力。

2.2 混凝土應(yīng)變

圖7為不同荷載下各模型梁混凝土應(yīng)變沿梁高的分布規(guī)律。由圖7可以看出：UHPC-T梁或普通混凝土T梁在開裂前處于彈性階段，中性軸位置基本保持不變，表明T形截面滿足平截面假定；UHPC-T梁或普通混凝土T梁開裂后，其中性軸位置出現(xiàn)逐漸上升。此外，部分測點(diǎn)出現(xiàn)突變，主要是由于該位置出現(xiàn)了裂縫所致。

2.3 荷載-跨中位移曲線

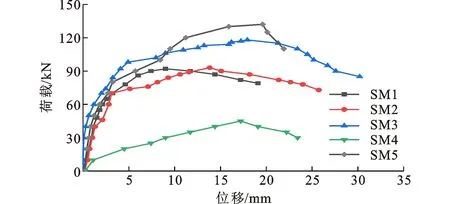
圖8給出了各模型梁荷載-跨中位移曲線。與SM4梁類似，SM1、SM2、SM3梁經(jīng)歷了彈性階段、裂縫開展階段和破壞階段3個(gè)不同受力階段。SM1、SM2、SM3梁的開裂荷載分別為48、46、50 kN，表明配筋率對(duì)UHPC-T梁的開裂彎矩影響不大，兩者最大相差約8.7%，這是因?yàn)閁HPC-T梁的開裂彎矩取決于UHPC水泥基體的抗拉能力。當(dāng)配筋率從0.209%增加至0.744%，相應(yīng)的極限荷載由92 kN提高至118 kN，增大了28.3%，表明配筋率的增加明顯提高了UHPC-T梁的極限承載力。此外，比較SM1梁和SM2梁可知，兩者的極限荷載非常接近，分別為92 kN和93 kN，表明UHPC-T梁為少筋梁時(shí)，提高配筋率不會(huì)提高其極限承載力，主要是因?yàn)樯俳盍旱臉O限承載力由受壓區(qū)混凝土控制。

3 預(yù)應(yīng)力對(duì)UHPC-T梁抗彎性能的影響

3.1 裂縫分布與抗裂性能

從圖5中SM2、SM5梁的裂縫分布可以看出，SM5梁(預(yù)應(yīng)力UHPC-T梁)與SM2梁(UHPC-T梁)相比，裂縫分布有如下特點(diǎn)：①試驗(yàn)梁首先在跨中部位出現(xiàn)第一條裂縫，隨著荷載繼續(xù)增加到80 kN，裂縫主要集中在加載點(diǎn)附近，非純彎曲段裂縫相對(duì)較少；②隨著荷載繼續(xù)增加到115 kN，除加載點(diǎn)外并未產(chǎn)生新的裂縫；③與SM2梁相比，SM5梁裂縫數(shù)量和主裂縫寬度都明顯減小，表明施加預(yù)應(yīng)力可以有效減少裂縫寬度和數(shù)量。從圖5(b)、(e)可以看出，SM5梁的裂縫發(fā)展特征為：隨著荷載的增加，裂縫寬度逐漸變大，裂縫不斷向上擴(kuò)展，但是少有裂縫發(fā)展到翼緣部分；當(dāng)荷載持續(xù)增加時(shí)，梁的裂縫數(shù)量和寬度逐漸增多，裂縫中不斷有UHPC粉末掉下來，并伴隨有鋼纖維斷裂的聲音，但直到試驗(yàn)由于破壞而停止，其受壓區(qū)混凝土未被壓碎。

從圖6給出的SM2梁和SM5梁的荷載與最大裂縫寬度關(guān)系可以看出，與SM2梁相比，SM5梁由于施加了預(yù)應(yīng)力，初裂過后其對(duì)裂縫寬度有限制作用，使得開裂過后裂縫發(fā)展緩慢，比如SM2和SM5梁的開裂荷載對(duì)應(yīng)的最大裂縫寬度均為0.01 mm，而加載至80 kN時(shí)對(duì)應(yīng)的最大裂縫寬度分別為0.26 mm和0.12 mm，表明施加預(yù)應(yīng)力可以阻止UHPC-T梁裂縫的發(fā)展。此外，SM2和SM5梁極限荷載對(duì)應(yīng)的最大裂縫寬度從1.85 mm降至1.41 mm，表明施加預(yù)應(yīng)力可以增大梁的抗裂性能和安全性能。

3.2 混凝土應(yīng)變

從圖7(b)、(e)給出的不同荷載下SM2梁和SM5梁混凝土應(yīng)變沿梁高的分布規(guī)律可以看出：UHPC-T梁和預(yù)應(yīng)力UHPC-T梁在開裂前處于彈性階段，其中性軸位置基本保持不變，表明T形截面滿足平截面假定；UHPC-T梁和預(yù)應(yīng)力UHPC-T梁開裂后，其中性軸位置出現(xiàn)逐漸上升。此外，部分測點(diǎn)出現(xiàn)突變，主要是由于該位置出現(xiàn)了裂縫所致。

3.3 荷載-跨中位移曲線

從圖8中的SM2、SM5梁荷載-跨中位移曲線可以看出，SM5梁與SM2梁類似，經(jīng)歷了彈性階段、裂縫開展階段和破壞階段3個(gè)不同受力階段。SM2、SM5梁的開裂荷載分別為46 kN和50 kN，兩者相差約8.7%，表明施加預(yù)應(yīng)力對(duì)UHPC-T梁的開裂彎矩影響不大，這是因?yàn)閁HPC-T梁的開裂彎矩取決于UHPC水泥基體的抗拉能力。由于SM5梁施加了預(yù)應(yīng)力，相應(yīng)的極限荷載由93 kN提高至132 kN，增大了42%，表明施加預(yù)應(yīng)力可以明顯提高UHPC-T梁的極限承載力。

4 理論計(jì)算

根據(jù)截面應(yīng)力分析法，分別計(jì)算普通混凝土和UHPC-T梁的開裂彎矩Mcr和極限彎矩Mu[16-17]。

開裂彎矩：

Mcr=(σp+γft)W0

(1)

(2)

λr=ρflf/df

(3)

式中：γ為截面塑性抵抗系數(shù)；βf為抗裂影響系數(shù)；λf為鋼纖維含量特征值；ρf為鋼纖維體積率；lf為鋼纖維長度；df為直徑；ft為UHPC軸心抗拉強(qiáng)度；W0為換算截面對(duì)截面受拉邊緣的彈性抵抗矩；S0為換算截面計(jì)算纖維以上或以下部分面積對(duì)截面重心軸的面積矩；σp為預(yù)應(yīng)力在構(gòu)件抗裂邊緣產(chǎn)生的預(yù)壓應(yīng)力。

根據(jù)公式(1)～(3)得到各T梁的理論開裂彎矩，列于表4中。

極限彎矩：

(1)若T形截面特性符合公式(4)，中性軸在翼緣內(nèi)，考慮腹板受拉區(qū)UHPC的抗拉作用，按公式(5)進(jìn)行正截面抗彎承載力Mu計(jì)算。

(4)

(5)

UHPC受壓區(qū)高度應(yīng)按式(6)計(jì)算。

表4 各模型梁開裂彎矩理論值與試驗(yàn)值對(duì)比Table 4 Comparisons between computational and experimental values of cracking-resistance moment of model beams

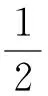
(hf-x)+fpyAp

(6)

(2)當(dāng)不符合公式(4)時(shí)，中性軸在腹板內(nèi)，應(yīng)考慮截面中腹板的受壓作用，其正截面抗彎承載力應(yīng)按式(7)計(jì)算。

(x-hf)2+fpyAp(h0-ap-x)

(7)

UHPC受壓區(qū)高度按式(8)計(jì)算。

fyAs+βftdb(h-x)+fpyAp

(8)

式中：β為受拉區(qū)UHPC等效矩形應(yīng)力系數(shù)；fcd為UHPC軸心抗壓強(qiáng)度設(shè)計(jì)值；fck為UHPC軸心抗壓強(qiáng)度標(biāo)準(zhǔn)值；ftd為UHPC軸心抗拉強(qiáng)度；As為受拉鋼筋總面積；fy為鋼筋屈服強(qiáng)度；fpy為預(yù)應(yīng)力筋抗拉強(qiáng)度設(shè)計(jì)值；AP受拉區(qū)縱向預(yù)應(yīng)力筋的截面面積；ap為受拉區(qū)縱向預(yù)應(yīng)力筋合力點(diǎn)至截面受拉區(qū)邊緣的距離；hf為翼緣高度；h為截面高度；h0為截面有效高度；bf為翼緣寬度；b為腹板寬度；x為受壓區(qū)高度。

通過計(jì)算，試驗(yàn)梁受壓區(qū)高度x在翼緣hf內(nèi)，適用于公式(4)，根據(jù)公式(5)得到相應(yīng)的計(jì)算結(jié)果(表4)。由表4可知：UHPC-T梁的開裂彎矩試驗(yàn)值與理論值的比值在0.81～0.89之間，相應(yīng)的比值均小于1，最大相對(duì)誤差為18.6%；其主要原因是本文計(jì)算公式采用的抗裂影響系數(shù)βf主要與鋼纖維摻量及種類有關(guān)，且與鋼纖維摻量成正比，同時(shí)它是根據(jù)鋼纖維質(zhì)量分?jǐn)?shù)為3%的試驗(yàn)數(shù)據(jù)回歸得到[16]，導(dǎo)致公式(1)針對(duì)本文鋼纖維質(zhì)量分?jǐn)?shù)為2%的試驗(yàn)?zāi)Ｐ偷挠?jì)算結(jié)果偏大。UHPC-T梁(SM1～SM3)的極限彎矩試驗(yàn)值與理論值的比值從1.054降至0.811，最大相對(duì)誤差為11.9%，其原因是本文公式計(jì)算采用的受拉區(qū)UHPC等效矩形應(yīng)力系數(shù)β取0.90，它主要與配筋率有關(guān)，且隨著配筋率增大而逐漸減小，導(dǎo)致采用公式(5)計(jì)算的理論極限彎矩隨配筋率的增大而增大，即配筋率從0.209%(SM1)增大至0.744%(SM3)，相應(yīng)的試驗(yàn)值與理論值的比值從1.054降至0.811。因此，SM2和SM3的極限彎矩理論值大于相應(yīng)的試驗(yàn)值。

5 結(jié)語

(1)在相同配筋率下，預(yù)應(yīng)力UHPC-T梁裂縫寬度和數(shù)量比UHPC-T梁少，表明施加預(yù)應(yīng)力能提高構(gòu)件的抗裂性，可抑制裂縫生成與發(fā)展。與UHPC-T梁相比，普通混凝土T梁裂縫數(shù)量相對(duì)較多且寬度更大，表明UHPC-T梁具有更優(yōu)越的抗彎和抗裂性能。

(2)配筋率對(duì)UHPC-T梁開裂荷載的影響不大；相同配筋率下，預(yù)應(yīng)力UHPC-T梁的極限承載力約為UHPC-T梁的1.4倍，UHPC-T梁的極限承載力約為普通混凝土T梁的2倍，表明預(yù)應(yīng)力和UHPC均可明顯提升T梁的承載能力。

(3)各試驗(yàn)梁跨中正截面混凝土應(yīng)變與荷載基本呈正比例關(guān)系，表明平截面假定同樣適用于預(yù)應(yīng)力UHPC-T梁與UHPC-T梁。

(4)UHPC-T梁的理論開裂彎矩和極限彎矩與相應(yīng)的試驗(yàn)結(jié)果吻合較好，試驗(yàn)值與相應(yīng)理論值之間的相對(duì)誤差不超過20%，滿足工程設(shè)計(jì)要求，表明該理論計(jì)算公式可用于預(yù)測或設(shè)計(jì)UHPC-T梁的關(guān)鍵性能參數(shù)。