基于多通道一維卷積神經網絡的刀具磨損動態預測模型

黃 華， 姚嘉靖， 王永和， 呂延軍

(1. 蘭州理工大學 機電工程學院，蘭州 730050； 2. 西安理工大學 機械與精密儀器工程學院，西安 710048)

刀具磨損程度的大小對工件的加工精度、機床的運行狀態以及刀具崩刃造成的生產安全問題都有極大影響[1]。為提高生產加工過程中的刀具利用率，減少停機換刀次數，增加工件表面的加工質量，需要建立一套準確的刀具磨損在線監測系統，為機床換刀提供可靠的決策手段。

一般常用的刀具磨損監測方法有直接法和間接法兩種。直接法利用光學測量，機器視覺等技術直接進行刀具磨損測量，但因成本與機身布局問題在應用中受到限制[2]。間接法一般通過傳感技術采集加工過程中的切削力、振動、聲發射、電流等信號，提取相關統計特征，再利用隨機森林[3]、支持向量機[4-5]、神經網絡[6]等機器學習模型建立特征與磨損值之間的映射關系，應用較為廣泛。特征提取后的機器學習建模領域，相關學者做了不同的研究。肖鵬飛等[7]提出了一種基于自適應動態無偏最小二乘支持向量機的刀具磨損預測模型，在一定程度上提高了建模效率。董彩云等[8]利用諧波小波包提取切削力各頻段的能量特征，將所得特征輸入回溯搜索算法優化后的最小二乘支持向量機，從而完成刀具磨損狀態的識別。淺層的機器學習算法由于提取特征的方式及篩選特征受限于人工經驗、操作頻繁、建模效率不高且費時費力，擁有更深網絡層次的深度學習[9]成為近幾年的研究熱點。深度學習可以看作是機器學習所有步驟的集成，可直接完成從傳感器原始信號數據到磨損值輸出的端到端建模任務。相比于傳統的機器學習建模方法，深度學習建模方法可自適應提取信號特征，再分別通過網絡內部分類層與回歸層完成刀具磨損狀態識別與回歸預測任務。曹大理等[10]提出了一種卷積神經網絡的建模方法，通過增加網絡深度自適應提取時域信號隱藏的微小特征，從而提高模型預測精度與泛化性能。劉思辰等[11]通過深度神經網絡來學習多模態輸入特征與刀具剩余壽命之間的復雜非線性關系。但是上述基于機器學習與深度學習建模方法的前提是假設不同的刀具磨損數據處于同一分布。而在實際加工過程中，即使在相同的加工工況下，由于機床安裝誤差、老化、走刀次數等因素，采集的信號數據分布存在差異[12]。因此用歷史數據訓練的預測模型在識別另一把刀具的磨損數據時會引起歷史模型失效、泛化性差等問題。

針對不同刀具磨損數據分布不一致造成的歷史模型失效問題，本文利用一維卷積神經網絡可自適應提取特征的特點，提出了一種基于多通道一維卷積神經網絡(1D-convolutional neural networks, 1D-CNN)的刀具磨損動態預測模型。首先，通過歷史刀具磨損數據建立初始的一維卷積神經網絡刀具磨損預測歷史模型。在此基礎上，利用遷移學習領域中的最大均值差異法(maximum mean difference, MMD)[13]對當前加工數據與歷史數據的分布一致性進行檢測判斷。數據分布相似時無需對歷史模型進行更新，可直接對數據進行磨損值預測。數據分布不一致時對歷史模型進行迭代更新，更新后的模型再對當前數據進行磨損預測。與傳統的刀具磨損預測模型相比，該方法從高維原始時域信號自適應提取刀具特征，可避免人工經驗造成的特征構造效率低、主觀性強等不利因素。此外，通過基于MMD算法的動態更新機制，模型可對不同刀具加工過程中出現的磨損數據分布不一致問題作出快速調整，來適應當前加工中的刀具磨損預測任務。

1 刀具磨損動態預測模型

1.1 問題描述

同一把刀具采集的歷史信號數據可表示為Xs={x1,x2,…,xn}，其中，n為采集樣本的個數。對于每個走刀樣本數據xn，均可表示為包含7種傳感器原始信號數據的七維特征向量形式xn={Fx,Fy,Fz,Vx,Vy,Vz,S}，其中，Fx，Fy，Fz，Vx，Vy，Vz，S分別為傳感器原始信號數據的XYZ三向切削力信號、XYZ三向振動信號與聲發射信號。與其對應的刀具磨損標簽為Ys={y1,y2,…,yn}，n為采集樣本的個數。以X方向切削力為例，數據Fx的矩陣形式可表示為

式中：h為采樣點數；n為樣本個數。

假設任一樣本數據xi屬于樣本空間χi，數據分布服從P(χi)。采集的另一把不同刀具的磨損數據可表示為Xt={x1,x2,…,xm}，任一樣本數據xj屬于樣本空間χj，數據分布服從P(χj)。由于機床安裝誤差、老化、走刀次數不同等因素，在相同工況下，歷史刀具磨損數據分布與在線采集的另一把刀具磨損數據分布存在差異，即P(χi)≠P(χj)。

基于歷史刀具的磨損數據Xs與標簽Ys對多通道1D-CNN模型進行有監督訓練，作為初始的刀具磨損預測歷史模型Mi。用歷史模型Mi對當前加工過程中另一把刀具的磨損數據Xt進行預測時，由于不同刀具磨損數據分布的差異性，使得歷史模型Mi失效。本文利用MMD算法對不同刀具的數據分布差異性進行研究，將歷史模型Mi不斷迭代更新，得到新的模型Mj，以適應當前刀具磨損預測任務。

1.2 七通道一維卷積神經網絡

本文利用七通道1D-CNN作為初始的刀具磨損預測歷史模型。將采集的XYZ三向切削力、XYZ三向振動、聲發射共7種傳感器信號數據作為七通道1D-CNN的輸入。通過數據歸一化處理，再依次通過6個卷積層、池化層運算，可對加工過程中的多種傳感器原始信號數據進行降維與信息融合，自適應提取原始時域信號數據中隱藏的特征信息，從而得到最優的特征表達。本文構建的七通道1D-CNN的輸入層將7個通道的信號分別按照采樣點數為5 000的長度進行截取，構建7×5 000×n的數據集，n為樣本個數。特征融合過程依靠6個卷積層與池化層運算進行融合。第1個卷積層對輸入的數據樣本進行一維、多通道、多卷積核的卷積運算，對樣本數據進行首次融合與特征提取，得到新的降維后的數據。第1個池化層根據卷積核步長對卷積層輸出進行最大值抽樣，再次對數據進行降維，可提高非線性特征的魯棒性。6個交替的卷積池化層可實現對七通道傳感器信號數據的層級式特征融合提取。(5 000，7)的數據矩陣經過自適應特征提取層得到一個長度為224的特征向量。最后利用全連接層完成特征到刀具磨損值的關系映射，實現刀具磨損預測。七通道1D-CNN刀具磨損預測模型，如圖1所示。

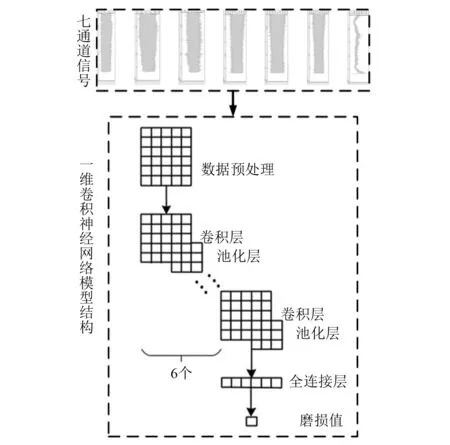
圖1 七通道1D-CNN網絡結構Fig.1 Structure of seven-channel 1D-CNN network

1.2.1 數據預處理

原始的傳感器信號數據包括Fx，Fy，Fz，Vx，Vy，Vz，S7種數據形式，經過數據裁剪，選擇各自信號的5 000個采樣點，組成5 000×7的原始信號矩陣。為了增加模型迭代速度，提高模型的預測精度，防止不同傳感器采集的信號數據由于量綱不統一造成建模過程中的梯度爆炸，可對數據進行歸一化處理，使數據轉化到[0-1]，計算公式為

(1)

式中：axis=s為第s個通道的原始時域信號；x為樣本數據的的采樣點；xmax為樣本數據的最大值；xmin為樣本數據的最小值。

1.2.2 卷積層

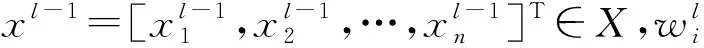
(2)

1.2.3 池化層

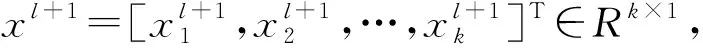
(3)

1.2.4 全連接層

經過多次卷積池化運算后，最后將輸出的多維數據經過全連接層將其轉化為一維特征向量的形式，即可實現卷積神經網絡對特征的自適應提取。假設經過多次卷積池化運算后的數據為xt-1，wt和bt分別為第t個全連接層的權重因子與偏置因子，最終全連接層的輸出可表達為

xt=Relu(wt·xt-1+bt)

(4)

本文所搭建的七通道1D-CNN模型經過數據預處理之后，再由6個交替的卷積池化層來提取特征，每個卷積層均使用Relu作為線性激活函數。網絡輸出層使用均方誤差(mean squared error,MSE)作為損失函數，表示真實的刀具磨損值與預測值的均方誤差，使用Adam優化器對模型進行迭代訓練，損失函數計算公式為

(5)

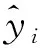
驗證過程中將歷史樣本數據作為訓練集用于歷史模型的訓練，當前刀具采集的樣本數據作為驗證集對模型進行評估。訓練集通過有監督的訓練方式對網絡進行訓練，驗證集作為評判模型預測精度的指標數據，不參與模型訓練。

1.3 動態建模方法

本節中，在1.2節建立初始的歷史模型基礎上，對所建模型進行動態更新。動態建模主要包括3個步驟：

步驟1利用帶標簽的歷史刀具磨損數據Xs建立初始的七通道1D-CNN刀具磨損預測模型Mi；

步驟2利用MMD算法計算當前刀具采集的信號數據Xt與歷史刀具磨損數據Xs的相似度α，相似度小于規定的閾值δ時，說明兩種數據分布基本相似，可直接利用歷史模型Mi對當前刀具信號進行磨損值預測；

步驟3當前信號與歷史信號的相似度α≥δ時，對歷史模型Mi進行迭代更新，得到新的模型Mj，更新后的模型Mj再對其進行磨損值預測。動態模型具體建模流程如圖2所示。

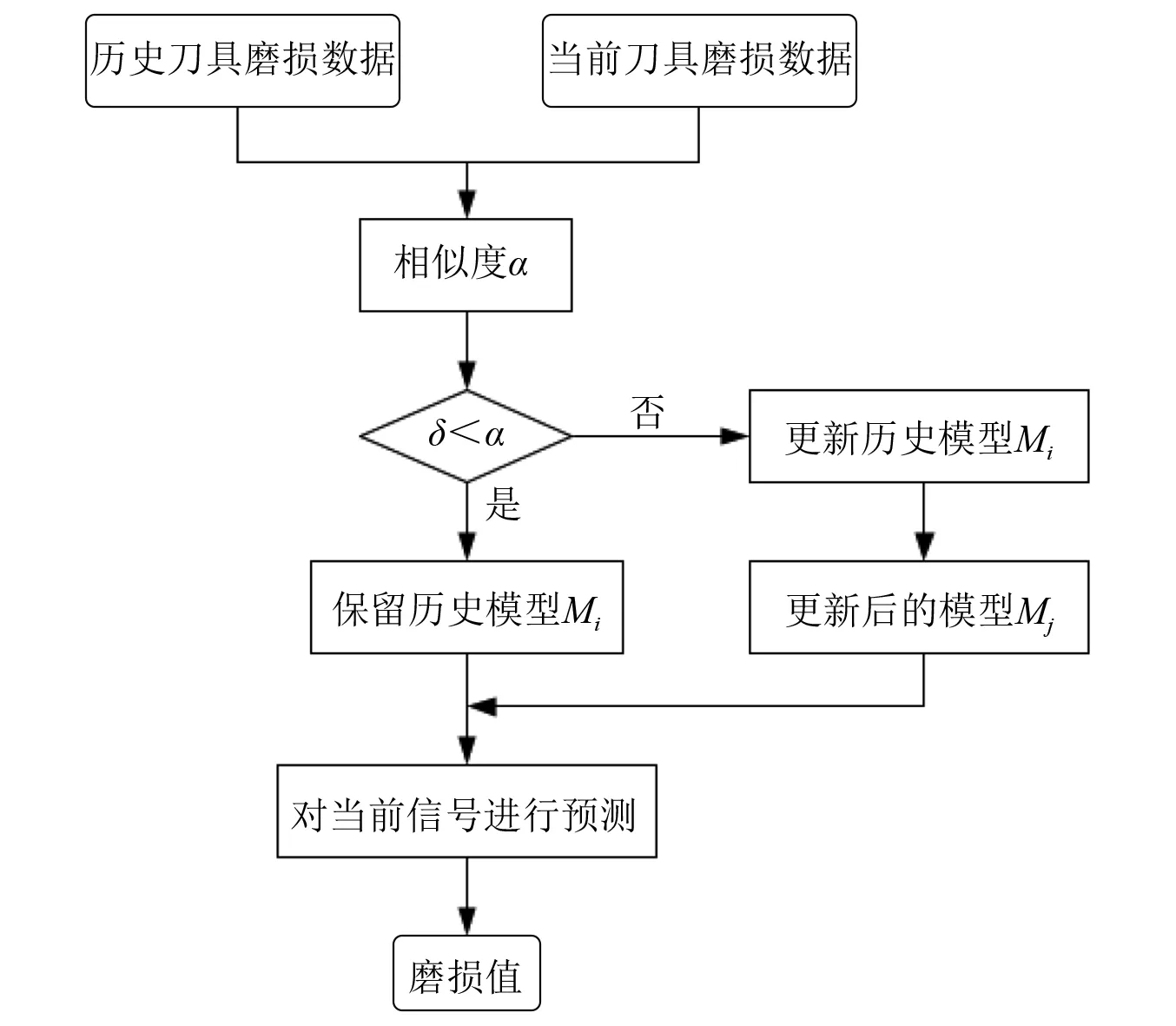
圖2 刀具磨損動態建模流程Fig.2 Process of tool wear dynamic modeling

數據分布相似度的計算方法利用MMD算法來描述。MMD值越小，說明兩種數據的分布差異越小，反之越大。MMD的基本原理是將兩種數據映射到高維空間計算其距離。計算公式為

(6)

式中：m，n分別為兩種數據的樣本總個數；H為該距離通過映射關系φ(·)將兩種數據映射到再生希爾伯特空間中進行度量國；K(·)為高斯核函數，由式(7)計算。

(7)

α=MMD2(Xs,Xt)

(8)

當前刀具磨損數據與歷史刀具磨損數據的閾值δ通過計算當前傳感器數據均值與歷史傳感器數據均值的MMD值，再求其平均值獲得。閾值δ表示單一傳感器下當前刀具走刀樣本數據與歷史數據走刀樣本數據的平均相似程度，具有普遍適用性，具體計算公式為

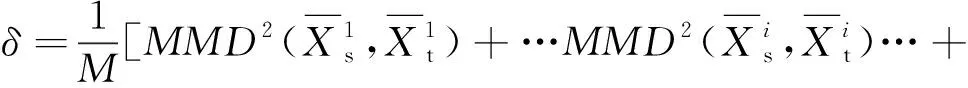
(9)

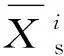
刀具磨損在線預測過程中，首先對切削過程中采集的7種傳感器信號數據，通過式(8)對當前刀具磨損數據與歷史刀具磨損數據進行相似度計算，并通過式(9)計算其對應的閾值。然后根據閾值與相似度的關系判斷當前模型是否更新。模型更新時，在歷史模型的基礎上加入新的預測數據和預測標簽對模型重新進行訓練。由于在線采集的當前刀具傳感信號沒有磨損標簽，此時可選擇當前刀具磨損數據與歷史刀具磨損數據相似度接近的走刀樣本的標簽數據。預測完成后將帶有標簽的磨損數據Xt添加到歷史刀具磨損數據中，不斷對模型進行補充，以提高模型的泛化性與穩定性。

2 試驗驗證

試驗驗證選用PHM2010數據挑戰賽中的數據集[14]。試驗中機床型號為Roders-TechRF，刀具為三齒碳化鎢球頭立銑刀，工件材料為HRC52不銹鋼。信號采集頻率50 kHz，每走刀一次采集XYZ三向切削力、XYZ三向振動、聲發射共7種原始時域信號。每次走刀完成后分別測得刀具三齒的磨損值，共計采集315次走刀樣本，磨損值標簽使用刀具三齒磨損值的平均值。試驗選擇帶磨損值標簽的C1、C4、C6數據集，用于模型精度驗證。切削參數如表1所示。

表1 切削參數Tab.1 Cutting parameters

試驗平臺中多通道1D-CNN模型使用Python語言Keras庫搭建，對比模型BP神經網絡(back propagation neural networks,BPNN)、隨機森林(random forest,RF)、模糊神經網絡(fuzzy neural networks,FNN)使用MATLAB語言建立。硬件設備使用Windows10操作系統，Intel Core處理器，8 G內存，NVIDA Geforce GTX 1650圖形處理器。

2.1 歷史模型預測分析

七通道1D-CNN模型參數的設計，主要是確定卷積核大小與神經元數目。一般在設計深度學習時遵循后一層神經元數目不超過前一層神經元數目的一半。本文前三個卷積層神經元數目均選擇32，后三個卷積層的神經元數目選擇16，卷積核大小均為2×1。這樣可降低卷積核的參數，有利于網絡的加深和防止過擬合。每個卷積層的后面都進行最大池化操作，池化步長通過調試設置為2×1和3×1。模型訓練參數的設置對模型的訓練精度影響較大。訓練批次(batch size)設置過小，影響訓練速度，損失函數與精度函數波動較大，模型難以收斂；設置過大，模型收斂過快，訓練不充分，預測精度較低。經過不斷調試，模型的訓練批次設置為10，訓練迭代次數(epochs)設置為30，學習率設為0.001，選擇Adam算法對模型的參數與超參數進行優化。模型的具體參數如表2所示。

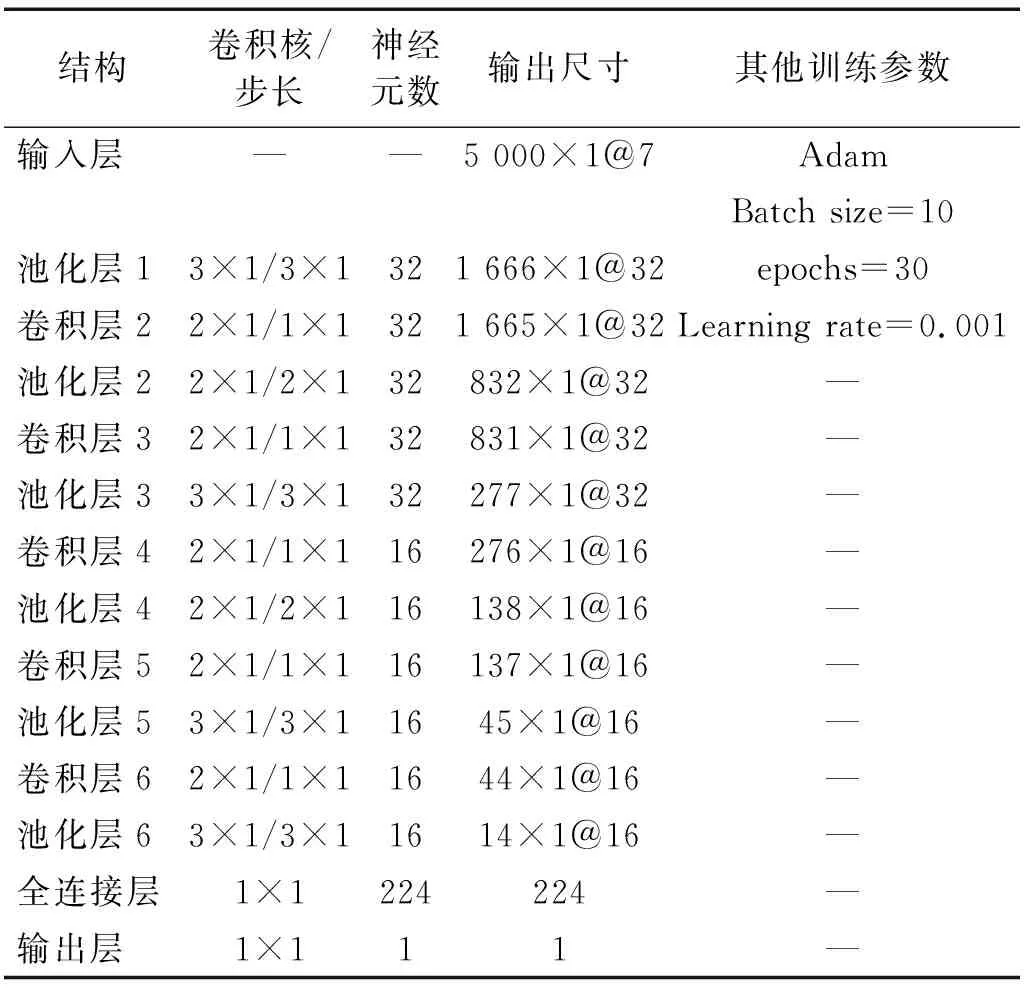
表2 七通道1D-CNN模型結構參數Tab.2 Structural parameters of seven-channel 1D-CNN model

將本文歷史模型1D-CNN模型與BPNN，RF，FNN 3種機器學習歷史模型進行比較，初步驗證本文1D-CNN的優越性。3種機器學習算法使用人工特征提取的方法，在信號數據中提取時域統計特征14個，頻域統計特征6個。原始信號數據的統計特征量指標具體如表3所示。

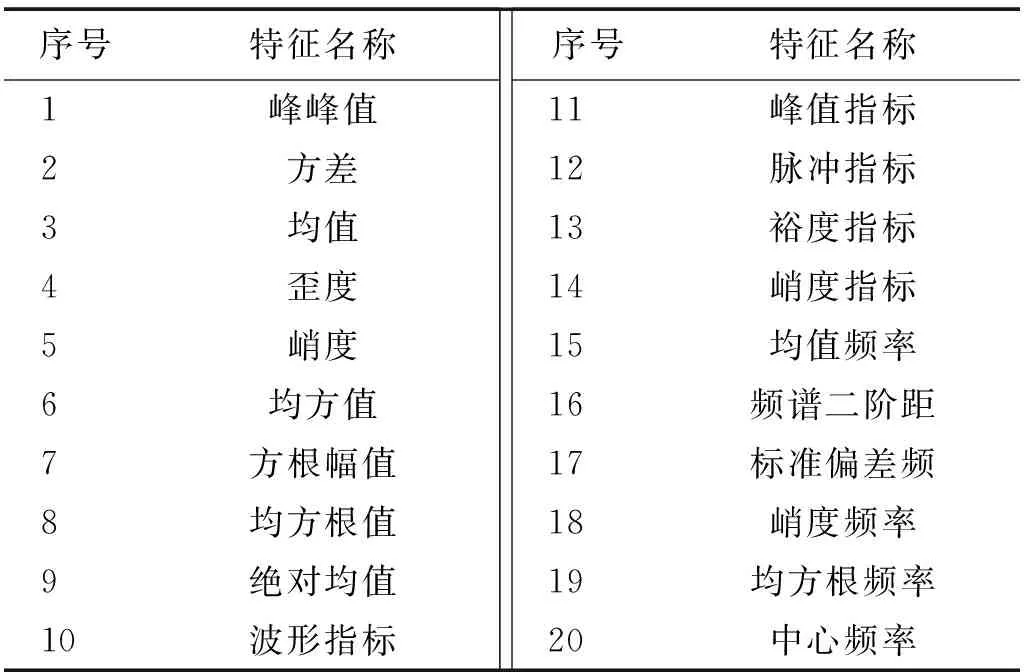
表3 特征指標Tab.3 Characteristics of the indicators

4種模型預測性能通過均方根誤差(root mean square error,RMSE)、平均絕對百分比誤差(mean absolute percentage error,MAPE)、決定系數(R2) 3種精度指標作為評判標準。指標RMSE，MAPE越小，指標R2越接近于1，表明模型的預測精度越高，3種評價指標的計算公式如下

(10)

(11)

(12)

將C1，C4，C6刀具磨損數據集分別用于七通道1D-CNN，BPNN，RF，FNN 4種模型的訓練與測試。其中將服從分布P(χ1)的C1刀具磨損數據集視為歷史磨損數據，用于模型訓練，服從P(χ2)與P(χ3)的其他兩把刀具的磨損數據集C4，C6用于模型測試。4種模型在C4，C6數據集上的預測結果如圖3～圖6所示。可以看出，基于C1刀具磨損數據建立的多通道1D-CNN，BPNN，RF，FNN歷史模型在預測C4，C6兩把刀具時，多通道1D-CNN預測效果稍微優于其他3種網絡模型，且多通道1D-CNN可自適應提取特征，因此本文將多通道1D-CNN作為初始的網絡預測模型。但由于兩種數據分布差異較大，4種歷史模型預測結果與實際值偏離較大，均會產生異常值。本文通過MMD相似度檢測方法將異常值篩選出來重新訓練初始1D-CNN模型，從而得到新模型，此時新模型就會獲取到異常值樣本與刀具實際磨損值的映射關系。因此新模型對異常值對應的這一類樣本進行重新預測時不會產生影響。

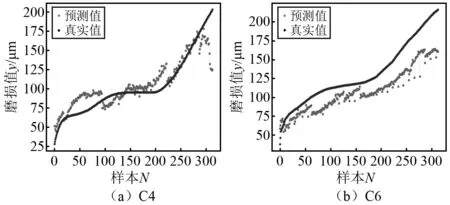
圖3 多通道1D-CNN模型預測結果Fig.3 Prediction results of multi-channel 1D-CNN model

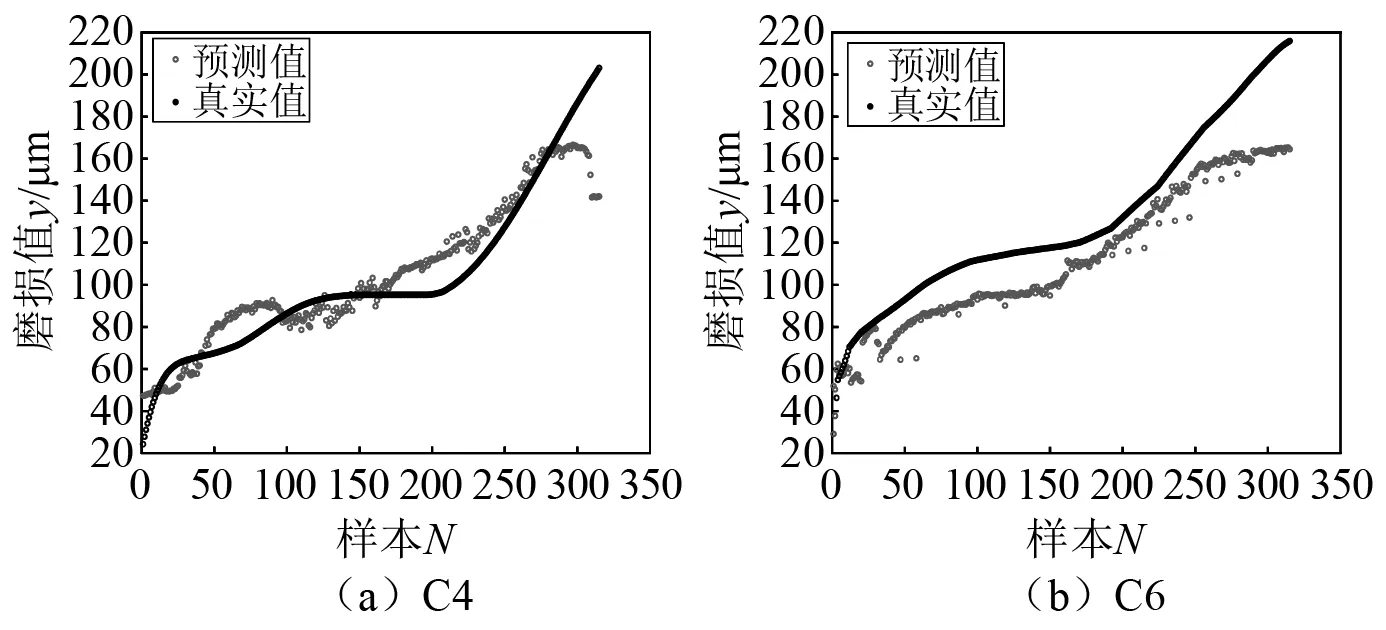
圖4 BPNN模型預測結果Fig.4 Prediction results of BPNN model

圖5 RF模型預測結果Fig.5 Prediction results of RF model

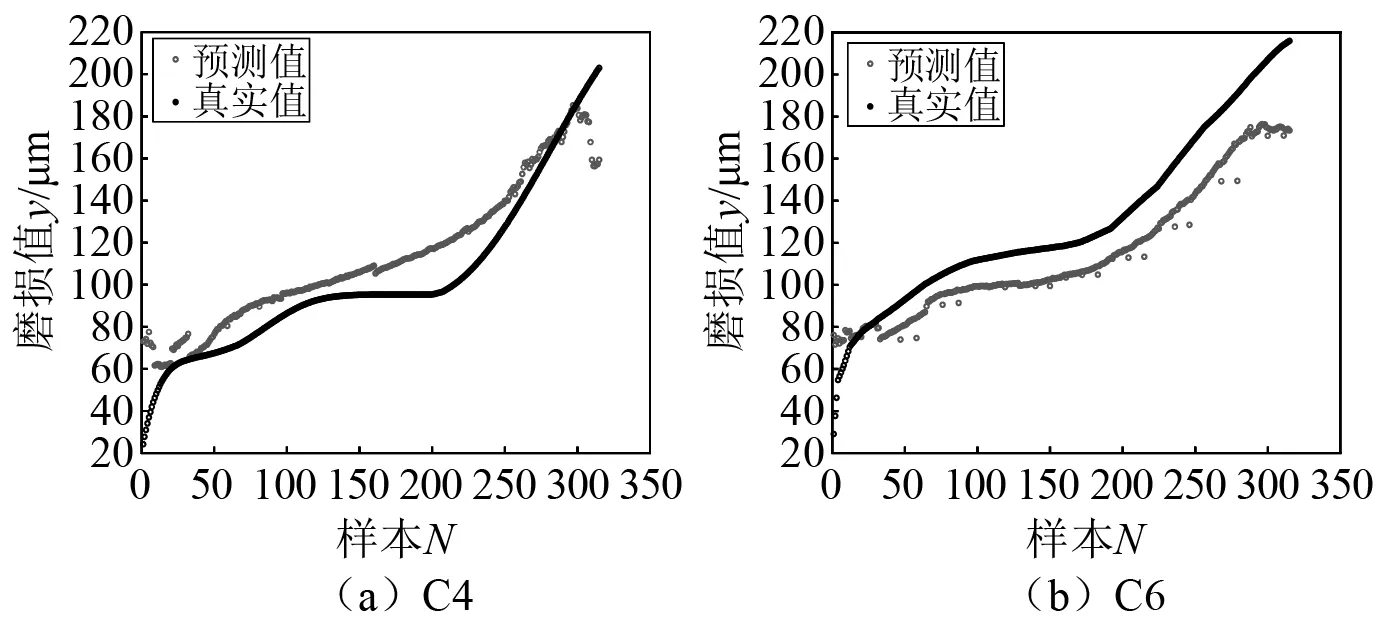
圖6 FNN模型預測結果Fig.6 Prediction results of FNN model

表4、表5分別為C4，C6兩把刀具在4種模型上的預測精度指標。可以看出，C4數據集的刀具磨損數據在4種模型中的驗證精度均優于C6數據集的刀具磨損數據，表明用于歷史刀具磨損數據進行建模的C1數據集的數據分布與C4數據集的數據分布相差較小，而與C6數據集的數據分布相差較大。

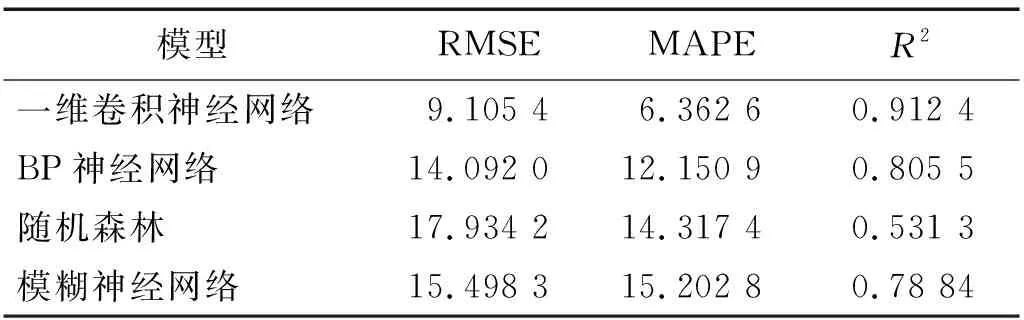
表4 C4預測結果精度對比Tab.4 Comparison of accuracy of C4 prediction results

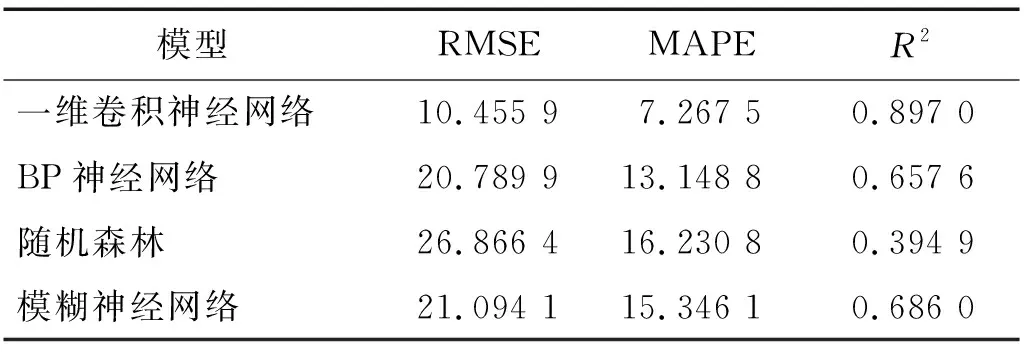
表5 C6預測結果精度對比Tab.5 Comparison of accuracy of C6 prediction results

以上分析表明，多通道1D-CNN在C4，C6兩把刀具上的預測精度均優于其他3種機器學習網絡模型。此外，由于數據分布差異性，使基于歷史數據C1數據集建立的歷史模型在C4，C6數據集的預測精度相差較大。為解決多通道1D-CNN歷史模型由于數據分布相似度相差較大導致的模型失效問題，有必要對歷史數據與當前數據進行MMD相似度檢測，從而對歷史預測模型進行迭代更新，以適應新的數據分布。

2.2 動態模型預測分析

用式(8)對歷史刀具C1與當前刀具C4，C6的每一次走刀數據進行MMD相似度計算，并通過式(9)分別求得C4，C6刀具的閾值δ。通過計算，C4與C6的閾值δ分別為0.188 7和0.046 9。C4，C6兩把刀具與歷史刀具C1每次走刀的數據分布相似度與其閾值的具體關系，如圖7所示。

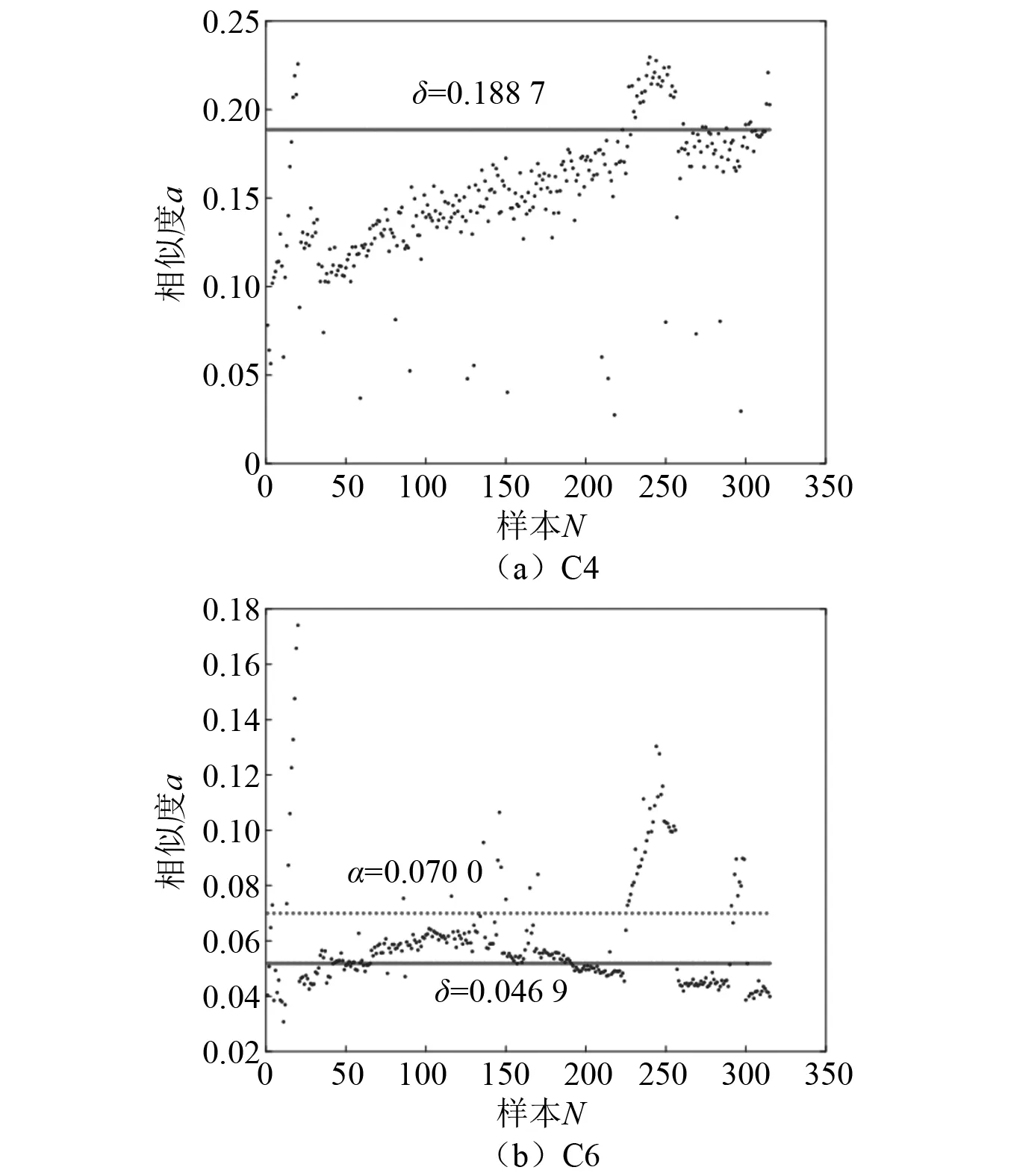
圖7 MMD相似度Fig.7 Similarity of MMD

可以看出，C4刀具走刀樣本數據與歷史刀具C1走刀樣本數據的相似度基本都在閾值以下，僅有少量走刀樣本的相似度大于閾值，表明這兩把刀具的磨損數據分布基本一致；C6刀具走刀樣本數據盡管與歷史刀具C1走刀樣本數據的相似度都基本大于閾值，但多數走刀樣本數據均在閾值附近，僅有少量的樣本數據相似度與閾值相差較大。這表明C1與C6兩把刀具的數據分布相差較大，但也存在相似關系，并不是相互獨立。這也驗證了2.1節中基于C1歷史刀具數據建立的4種歷史模型在C4刀具上的預測精度均高于C6刀具的試驗結果。通過對比相似度與閾值的關系，C6刀具的走刀樣本數據相似度多數高于閾值，但基本在閾值附近，可近似認為這些樣本數據與C1數據集對應的走刀樣本數據分布相同。而在相似度大于0.070 0時，部分走刀樣本數據相似度明顯偏離閾值，因此可將C6刀具的閾值δ取為0.070 0。動態模型訓練時，將C4，C6兩把刀具相似度α大于閾值δ的部分與C1數據集共同作為訓練數據集對模型進行迭代更新，模型更新后再對刀具磨損數據進行預測。更新后的模型在C4與C6數據集上預測結果如圖8、圖9所示，驗證精度指標如表6所示。

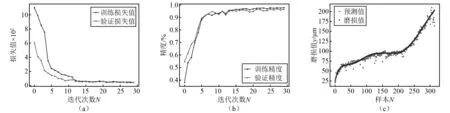
圖8 C4驗證結果Fig.8 Verification results of C4

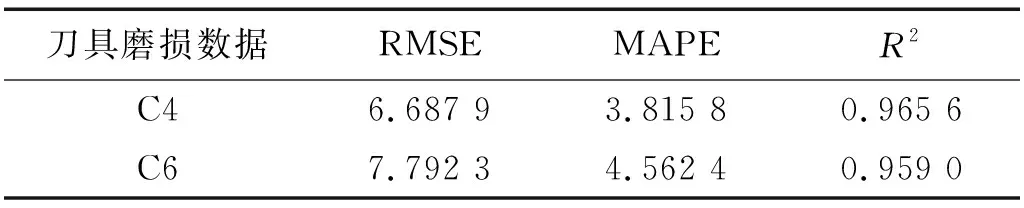
表6 預測結果精度對比Tab.6 Comparison of accuracy of prediction results

由圖8、圖9可以看出，訓練集與驗證集的損失函數和準確率在剛開始迭代訓練的前10次快速收斂，并在第15次迭代訓練時，曲線基本趨于穩定，沒有發生過擬合現象。根據C1，C4刀具最終的動態模型預測結果可以看出，兩把刀具的預測結果與真實磨損值在隨著切削時間的變化過程中，多數樣本預測值基本都在真實值附近，總體預測精度相較于初始的歷史預測模型有明顯提升。表6中精度指標在C4與C6數據集均保持在較高水平，表明模型訓練效果良好。對幾種模型訓練所用時間進行了統計，具體如表7所示。

表7 模型訓練耗時Tab.7 Model training time 單位：s

可以看出，盡管1D-CNN由于直接處理原始信號數據，自適應提取特征，耗時較長，但本文所提出的動態1D-CNN預測精度顯著高于其他幾種建模方法，可彌補耗時較長的不足。此外，相比于之前4種基于歷史數據的建模方法，本文所提出的動態建模方法具有較好的自適應能力與較高的預測精度，驗證了動態建模方法的有效性。

3 結 論

本文針對同一工況下不同刀具磨損數據的分布不一致問題，提出了一種基于多通道1D-CNN的刀具磨損動態預測建模方法，可有效提高不同刀具的預測精度，具體工作如下：

(1) 所搭建的七通道1D-CNN通過融合7種傳感器信號特征，可增加刀具磨損數據的多樣性；相比于傳統淺層機器學習模型，本文所建模型通過特征提取層自適應提取原始時域信號特征，可避免機器學習人工提取特征對建模精度的影響。

(2) 所提出的動態建模方法在保持較高預測精度的同時可提高模型的自適應性與魯棒性。通過引入遷移學習領域的MMD相似度判斷方法，對當前加工的刀具磨損數據與歷史刀具磨損數據不一致進行相似度檢測，在已有歷史模型的基礎上對模型進行迭代更新，從而建立動態刀具磨損預測模型，可適應加工過程中刀具磨損的不確定性。