基于自適應k近鄰的時間序列異常模式識別
王 玲 周 南 申 鵬
(北京科技大學自動化學院 北京 100083)
(工業過程知識自動化教育部重點實驗室(北京科技大學) 北京 100083)(lingwang@ustb.edu.cn)
目前,時間序列的異常檢測作為一項重要的數據挖掘任務,已被廣泛應用到氣象信息[1]、水文監測[2]、醫療保健[3]、工業應用[4]等眾多領域中.根據異常的表現形式不同,時間序列的異常可以分為異常點、異常序列及異常子序列[5].異常點是與大部分數據點有顯著差異的數據點[6-7];異常序列指的是與大部分時間序列有顯著偏差的整條時間序列[8-9];異常子序列是與大部分子序列有顯著不同的子序列[10-11].考慮到異常子序列可能與一段時間內的特殊事件有關,往往會比正常子序列包含更多有用的信息,更有研究價值,本文主要對異常子序列進行研究.
異常子序列并非只有一種,不同的機制[12]會導致多類異常子序列的產生.例如,心電圖的異常子序列即心率失常,可以分為竇性心動過速、早搏、房顫、竇性心動過緩、房室傳導阻滯等多種類型;水文時間序列中的異常子序列也可以分為洪水、干旱等多種異常類型.為了識別不同類型的異常,可以先檢測異常子序列,然后再利用聚類算法區分異常子序列的類型,令一個異常模式代表一類異常子序列,進而實現異常模式的識別.下面分別對異常子序列檢測和異常子序列聚類這2部分的相關工作進行說明.
目前, 常見的異常子序列檢測算法包括基于距離的異常子序列檢測方法[13-15]、基于聚類的異常子序列檢測方法[5,16]、基于密度的異常子序列檢測方法等[17-18].基于距離的異常子序列檢測方法利用子序列之間的距離計算子序列的異常分數(異常因子), 通過比較異常分數與設定閾值的大小來檢測異常子序列.文獻[13]提出一種基于距離的異常子序列檢測算法DBAD,通過計算兩兩子序列的歐氏距離,并比較其與分布中心的偏差程度實現異常子序列檢測.文獻[15]將子序列與其最近的k個子序列距離的平均值作為異常分數,并利用假設檢驗確定子序列是否異常.基于聚類的異常子序列檢測方法是將子序列劃分到不同的類簇中,使得簇中的子序列具有較高相似度,簇間的子序列具有較低相似度.通過分析子序列和類簇中心之間的關系,來尋找異常子序列.文獻[16]使用模糊c均值聚類[19]來揭示子序列的結構,然后利用從簇中心和劃分矩陣得到的重構準則[20]重建原始子序列,對于每個子序列,根據原始子序列與重建子序列的差值分配其異常分數.該聚類算法需要人為設置聚類個數,但在實際應用中,我們通常缺少對數據集的先驗知識,這會嚴重影響聚類的效果.而基于密度的異常子序列檢測方法是根據子序列的密度與其周圍子序列的密度之間的比值來定義異常分數,從而檢測出異常子序列.文獻[18]提出了一種動態局部密度估計(dynamic local density estimation, DLDE)異常子序列檢測算法,利用時間分割樹 (time split tree, TSTree)動態分割時間序列,并通過子序列中每個數據點的動態局部密度來評估子序列的異常程度;但該算法需要利用集成學習獲取參數,算法復雜度較大.
由于不同結構的異常子序列預示著不同的異常事件,因此需要對異常子序列進行聚類以區分不同類型的異常子序列,識別所有異常模式.這里介紹一些可用于聚類異常子序列的時間序列聚類算法.文獻[21]提出了一種基于軌跡形狀的時間序列聚類算法kmlShape,該算法是k均值聚類算法[22]的一個變體,利用弗雷歇距離計算出時間序列之間的距離,并提出弗雷歇平均值確定每個類別的均值以實現時間序列的聚類;文獻[23]提出一種基于統計預處理的距離密度聚類DDC,將平滑和特征選擇作為預處理步驟,在每個特性集群中進行距離密度聚類以完成時間序列聚類;文獻[24]提出了一個新穎的時間序列聚類算法,該算法可以生成同質且較好分離的聚類,其采用標準的互相關距離度量方法并基于此提出了一個計算簇心的算法,在每一次迭代中都用其來更新時間序列的聚類分配.然而,這些聚類算法對輸入參數較為敏感,影響最終聚類結果的正確性,這在一定程度上限制了這些聚類算法的應用.
文獻[21?24]中提出的算法在設置參數方面較為薄弱,且忽略了異常子序列的類別區分問題,因此,本文重新定義了異常模式這一概念,提出一種基于自適應k近鄰的異常模式識別算法(anomaly pattern recognition algorithm based on adaptiveknearest neighbor, APAKN).該算法首先根據各子序列的自適應k近鄰計算其自適應距離比和相對密度,這里相對密度與傳統基于密度的異常檢測算法[25]的局部密度有所區別,無需計算待測對象密度與其鄰域對象密度之比;然后提出一種基于最小方差的自適應閾值方法確定異常閾值;最后采用基于自適應k近鄰的聚類算法自動發現聚類中心并聚類異常子序列.整個算法過程在無需設置任何參數的情況下,不僅解決了密度不平衡問題,還精簡了傳統基于密度異常子序列檢測算法的步驟,實現良好的異常模式識別效果.
1 相關定義
定義1.子序列.給定一子序列集合D={s1,s2,…,, 其中為子序列的個數其中表示子序列所包含的數據點個數.
定義2.異常子序列和正常子序列.異常子序列是子序列集合中異常分數大于異常閾值的子序列,異常子序列集合表示為其中n為異常子序列的個數, 則正常子序列的個數為N?n,正常子序列集合表示為
定義3.異常模式.異常模式是由相似異常子序列構成的類簇的中心, 異常模式集合表示為P={p1,p2,…,pi,…,pc},其中c為聚類后的類簇個數.
定義4.子序列距離.對于子序列集D中任意2個子序列si,sj, 采用動態時間彎曲(dynamic time warping,DTW)距離[26]度量計算si與sj之間的距離
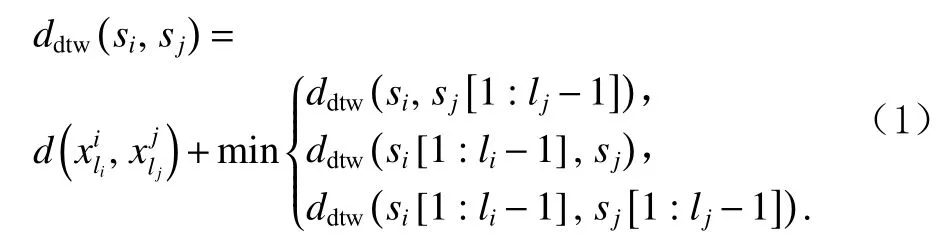
其中,si[1:li?1]為si去除尾元素后剩余的子序列,即去除尾元素后剩余的子序列,即表示數據點與數據點之間的歐氏距離,計算方法為 √
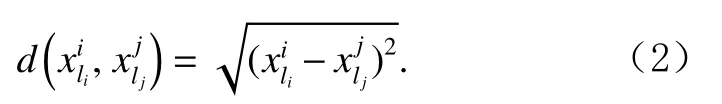
定義5.第k近 鄰 和 第k近 鄰 距 離.假 設si和sj為 子序列集D中 的子序列,對于任意正整數k,si的第k近鄰為sj,si的 第k近 鄰 距 離 為si與sj之 間 的 距 離,記為kdk(si),sj需要滿足2個條件:
1)D中 至 少 存 在k個 子 序 列sj′, 使kdk(si)成立;
2)D中 最多存在k?1個子序列sj′,使kdk(si)成立.
定義6.k近鄰域.子序列集合D中 ,除si外所有與si的距離小于等于si的第k近鄰距離kdk(si)的子序列構成子序列si的k近鄰域KNNk(si),即
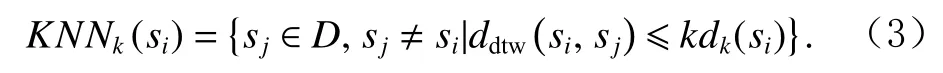
將KNNk(si)中子序列的個數定義為si的k近鄰個數,記為 |KNNk(si)|.
定義7.反向k近鄰域.對于任意子序列,如 果si屬 于sj的k近 鄰 域 , 則sj屬 于si的 反 向k近 鄰 域RNNk(si),即
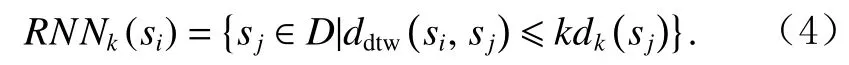
將RNNk(si)中子序列的個數定義為si的 反向k近鄰個數,記為 |RNNk(si)|.
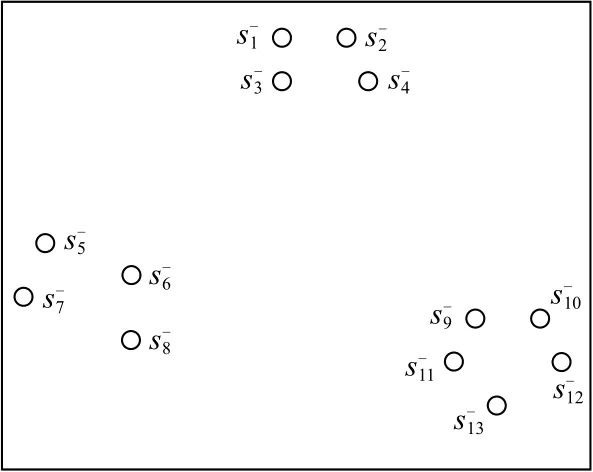
為說明k近鄰域和反向k近鄰域,圖1利用7個空心圓分別表示7個子序列,顯示出各子序列之間的距離關系.表1列出近鄰值k=4時7個子序列的k近鄰域、反向k近鄰域、反向k近鄰個數.
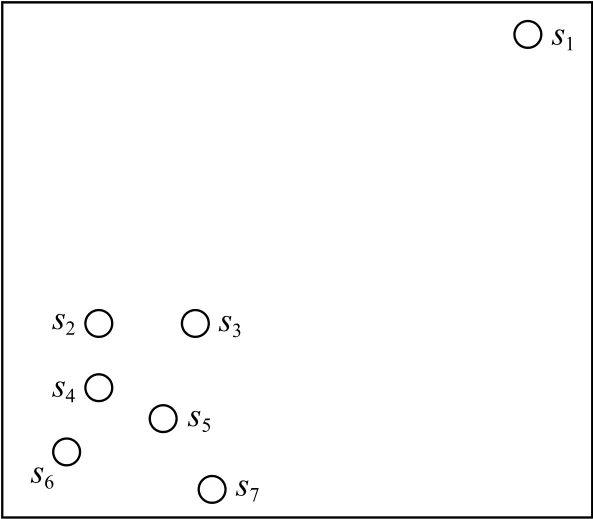
Fig.1 Schematic diagram of subsequence distribution圖1 子序列分布示意圖

Table 1 k Near Neighbors Domain and Reverse k Near Neighbors Domain of Subsequences when k = 4表1 k = 4時子序列的k近鄰域與反向k近鄰域
從表1可以看出,同一子序列的k近鄰域和反向k近鄰域并不存在對稱關系.
2 基于自適應 k近鄰的異常模式識別算法
APAKN是一個基于自適應k近鄰的異常模式識別算法,算法整體工作流程如圖2所示,主要由異常子序列檢測和異常子序列聚類2個部分組成.本節將對 APAKN 算法的基本思想及其實現過程進行詳細介紹.
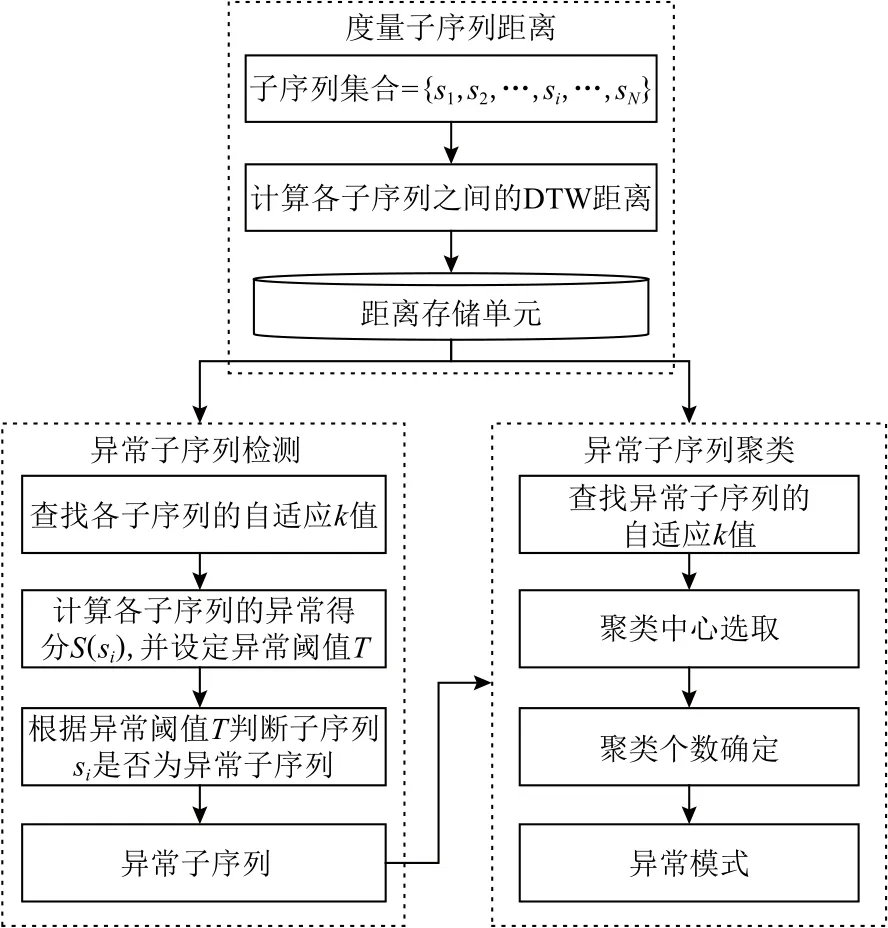
Fig.2 The overall workflow of the APAKN圖2 APAKN的總體工作流程
2.1 基于相對密度的異常子序列檢測
為了確定子序列是否異常,查詢各子序列的自適應k近鄰值計算子序列的相對密度,根據相對密度計算異常分數,將異常分數大于異常閾值的子序列視為異常子序列.
考慮到異常子序列具有較少的鄰居,正常子序列具有較多的鄰居,各子序列的k近鄰值并不相同是自適應k近鄰搜索算法區別于傳統k近鄰[27]算法的主要特征.搜索子序列si(si∈D)的自適應k近鄰值ki的主要過程為:令搜索次數r=1,迭代地尋找每個子序列的r近鄰 域,使用Numr記 錄 第r次迭代時集合中0的個數.若Numr在連續3次迭代中未發生變化,即Numr=Numr+1=Numr+2,則認為算法達到穩定狀態,迭代停止,否則,令r=r+1繼續迭代.將迭代停止后的迭代次數計為kf=r+2,子序列si的 自適應k近鄰值
以圖1中的子序列為例查找各子序列的自適應k近鄰值.圖3展示了7個子序列在r=1,r=2,r=3,r=4時的近鄰情況.
當r=1時, 圖3 (a)展示了所有子序列的 1近鄰,其 |RNN1(si)|=0的子序列為s1,s6,s7, 此時Num1=3.
當r=2 時,圖3 (b)展示了所有子序列的2近鄰,{|RNN2(si)|}i=1={0,3,2,3,4,1,1} ,其 |RNN2(si)|=0 的子序列為s1, 此時Num2=1.
當r=3 時, 圖3 (c)展示了子序列s1,s5的3近鄰,{|RNN3(si)|}7i=1={0,4,3,5,6,2,1},其 |RNN3(si)|=0的子序列為s1, 此時Num3=1.
當r=4 時, 圖3 (d)展示了子序列s1,s5的4近鄰,{|RNN4(si)|}7i=1={0,4,5,6,6,4,3},其 |RNN4(si)|=0的子序列為s1, 此時Num4=1.
當r=2 時滿足Num2=Num3=Num4, 搜索停止,kf=r+2=4, 輸出所有子序列的自適應k值為{k1,k2,…,k7}={0,4,5,6,6,4,3}.
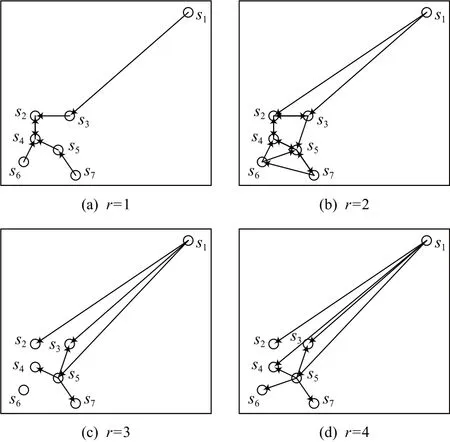
Fig.3 Neighbors of subsequences at different values of r圖3 子序列在不同 r值時的近鄰情況
在得到子序列si(i=1,2,…,N)的自適應k近鄰值ki(i=1,2,…,N)的基礎上,計算子序列的相對密度來進一步得到子序列的異常分數.許多復雜的數據集可能有多個密度不同的集群,如果只比較局部密度的大小可能會將一些密度較小集群中的數據對象誤檢為異常.為解決密度不平衡問題,目前基于密度的異常子序列檢測算法通常在估計出所有子序列的局部密度后,通過比較待測子序列的局部密度與其鄰域內子序列的局部密度來檢測異常,但算法結果對鄰域參數較為敏感,人工選擇合適的鄰域參數較為困難,需要研究者的經驗或大量的實驗,也使算法不具備自適應性.為此,本文引入自適應距離比計算相對密度,不僅解決密度不平衡問題,而且無需人為選擇近鄰參數.
令km為集合 {k1,k2,…,kN}中的最大值,為子序列si的km近鄰域中的子序列,為子序列的自適應k近鄰值,si與的距離為,的第近鄰距離為,計算si與其km近鄰域KNNkm(si)內所有子序列的自適應距離比.子序列si相對于子序列的自適應距離比為
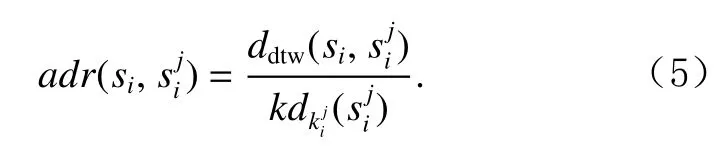
計算子序列si(si∈D)的相對密度,其為si與其所有KNNkm(si)內子序列的平均自適應距離比的倒數,KNNkm(si)中的子序列個數用表示.si的相對密度計算公式為
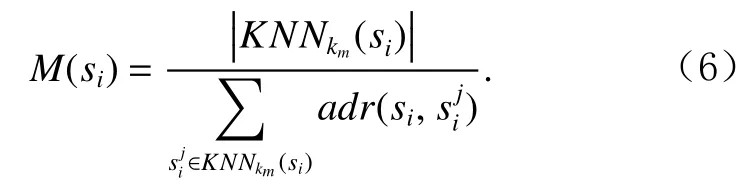
以圖4為例說明自適應距離比如何解決密度不平衡問題.圖4中s8,s9,s10屬于高密度集群,s11為異常子序列,s12,s13,s14,s15,s16屬于低密度集群.若是單純將密度小的子序列視為異常,則低密度集群都有可能被視為異常.這里以s8,s11,s14為例證明自適應距離比解決密度不平衡問題的有效性.在該示例中km=8,圖4中已標注出s8,s11,s14的8近鄰域范圍,表2列出km=8時s8,s11,s14相對于其第8近鄰的自適應距離比.
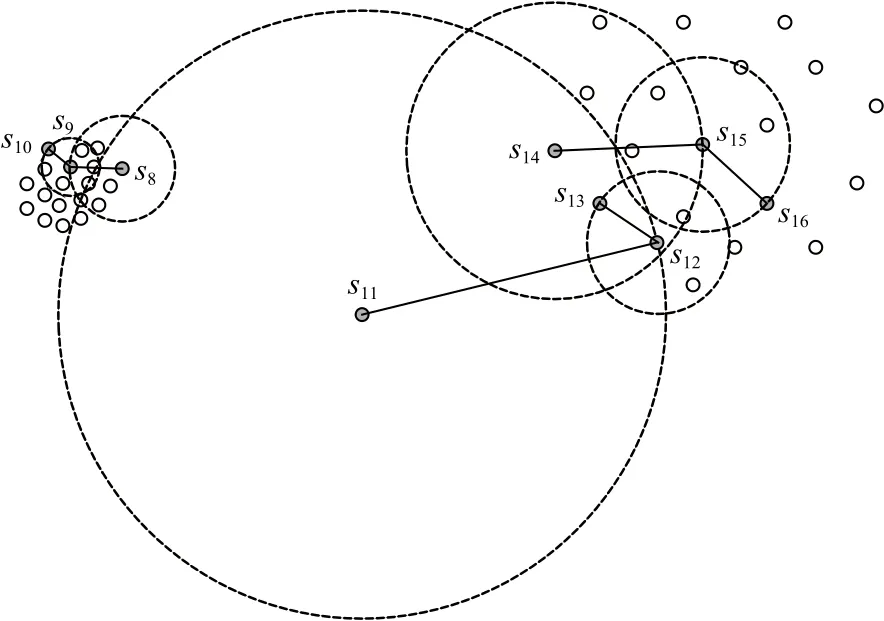
Fig.4 Density imbalance data圖4 密度不平衡數據

Table 2 Adaptive Distance Ratio of s8, s11, s14 Relative to Its 8th Nearest Neighbor表2 s8, s11, s14相對于其第8近鄰的自適應距離比
從表2可以看出adr(s8,s9)與adr(s14,s15)相差較小,而adr(s11,s12)遠大于adr(s8,s9)和adr(s14,s15),根據相對密度的計算公式(6)可以推斷出M(s8)與M(s14)的值大致相同,而M(s11)遠小于M(s8)和M(s14)的值.這可以證明本文提出的自適應距離比和相對密度不受其所屬集群密度的影響,解決了密度不平衡問題.
子序列相對密度較低意味著其可能具有較高的異常分數.進一步,子序列si的異常分數為
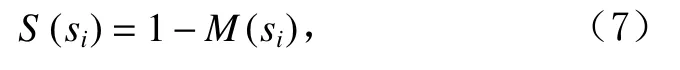
得到異常分數集合S={S(s1),S(s2),…,S(si),…,S(sN)}后,對其做歸一化處理,子序列si的最終異常分數為
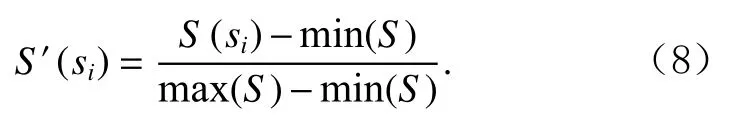
以圖1中s1為例計算異常分數:由于{k1,k2,…,k7}={0,4,5,6,6,4,3},所以該集合中的最大值km=6,為子序列s1的6近鄰域中的子序列,即(j=1,2,…,6)∈KNN6(s1)={s3,s2,s5,s4,s7,s6},為子序列的自適應k近鄰值,s3,s2,s5,s4,s7,s6的自適應k近鄰值分別為5,4,6,6,3,4,s3,s2,s5,s4,s7,s6的第近鄰分別是s6,s6,s1,s1,s4,s7,因此的第近鄰距離分別為ddtw(s3,s6),ddtw(s2,s6),ddtw(s5,s1),ddtw(s4,s1),ddtw(s7,s4),ddtw(s6,s7);代入式(6)可以得到M(s1)=0.413,s1的原始異常分數為S(s1)=1?M(s1)=0.586,歸一化異常分數為S′(s1)=1,后文中若無特殊說明,異常分數即是指歸一化后的異常分數.
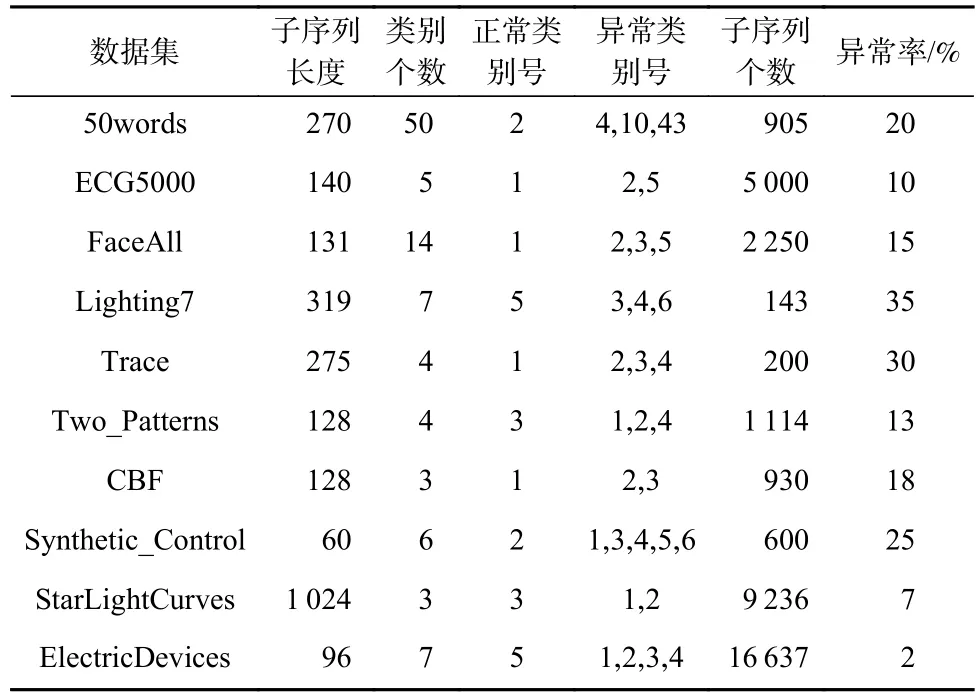
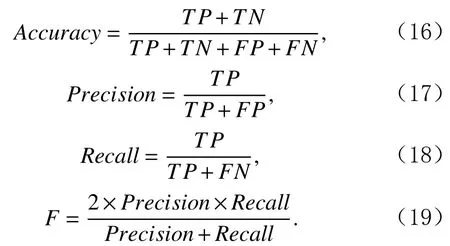
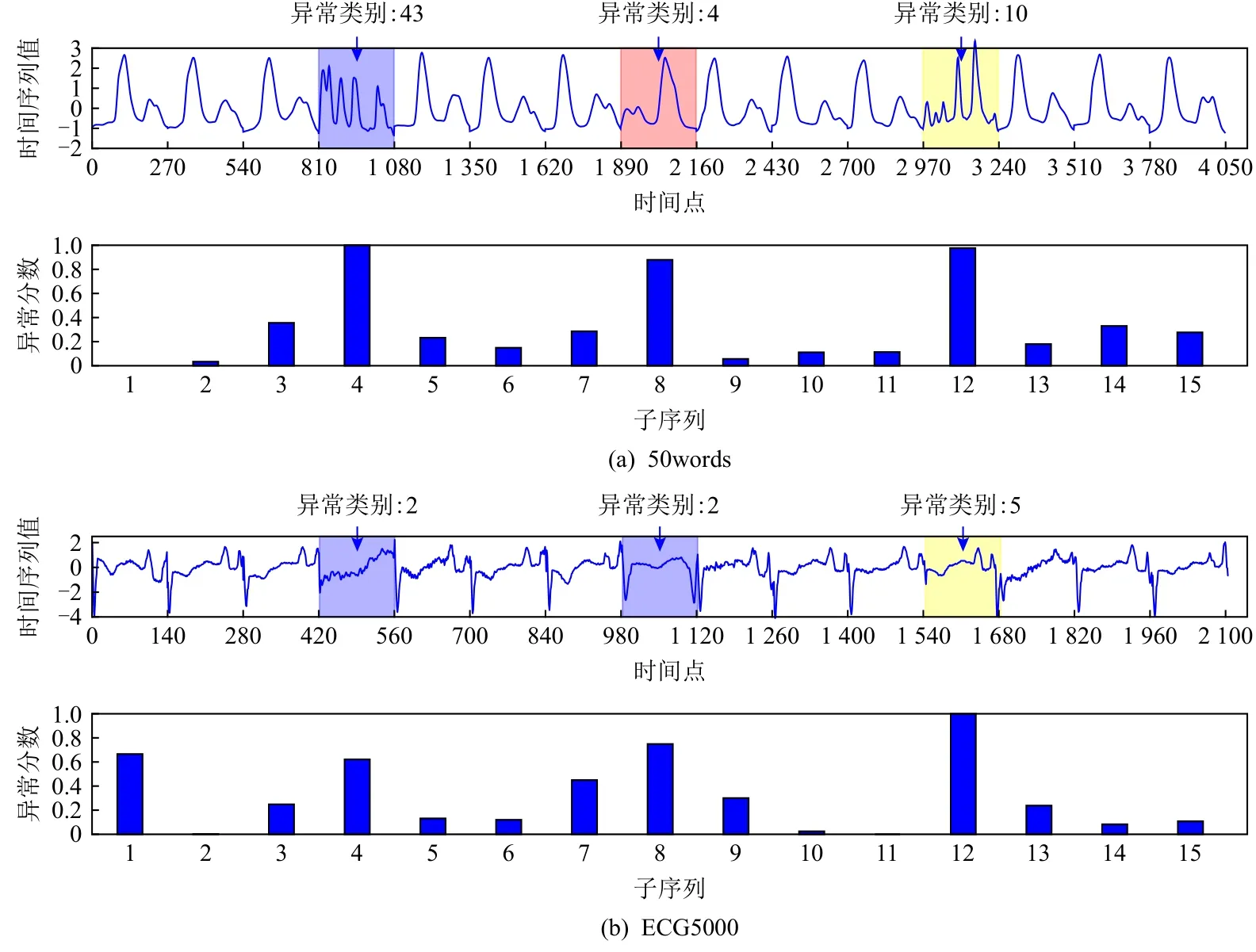
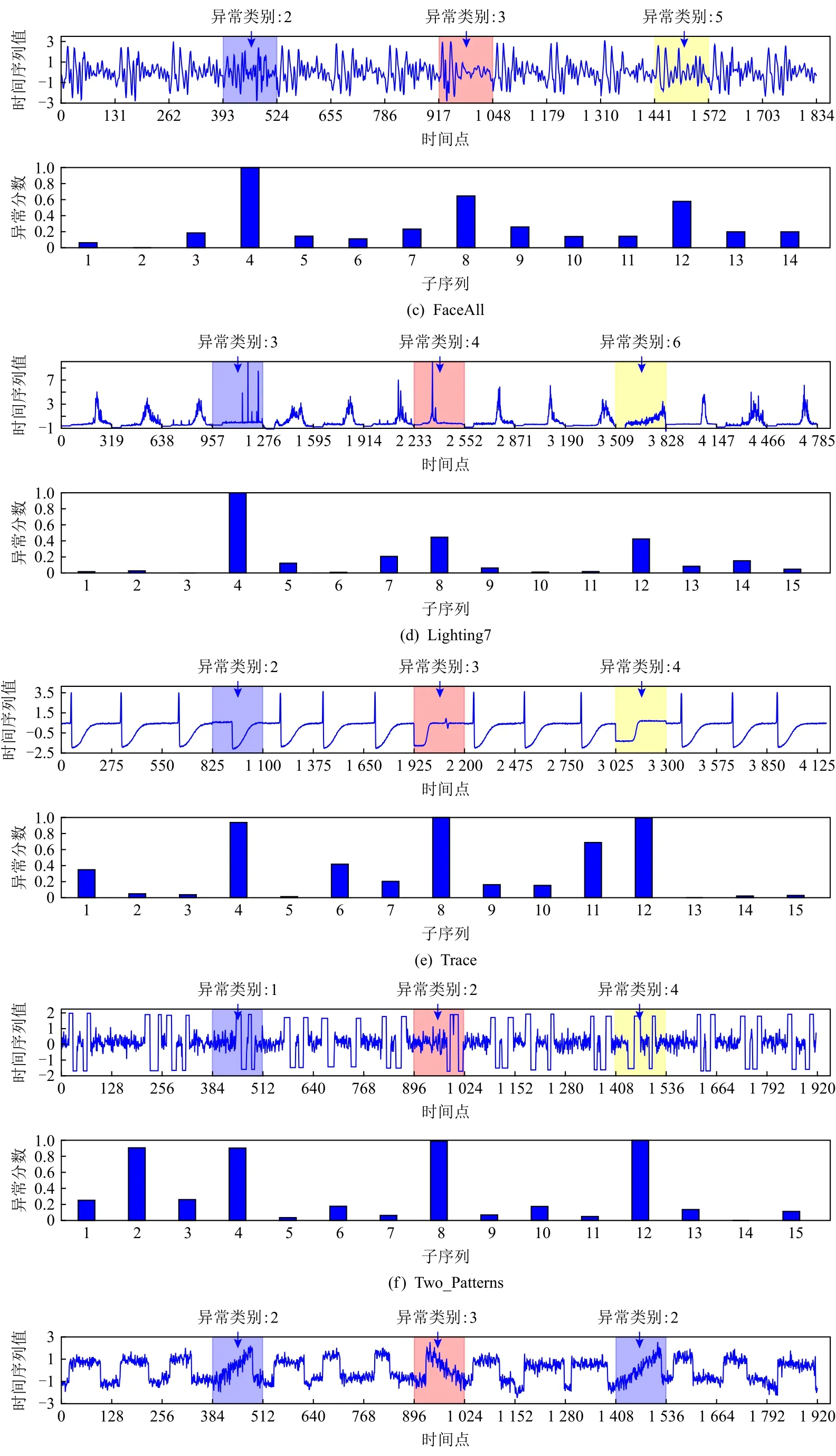
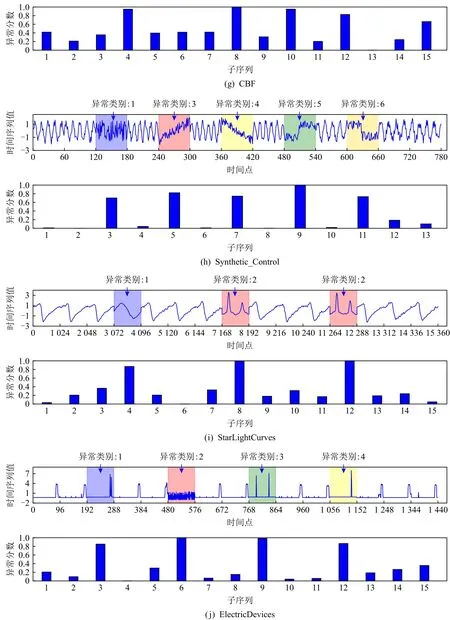
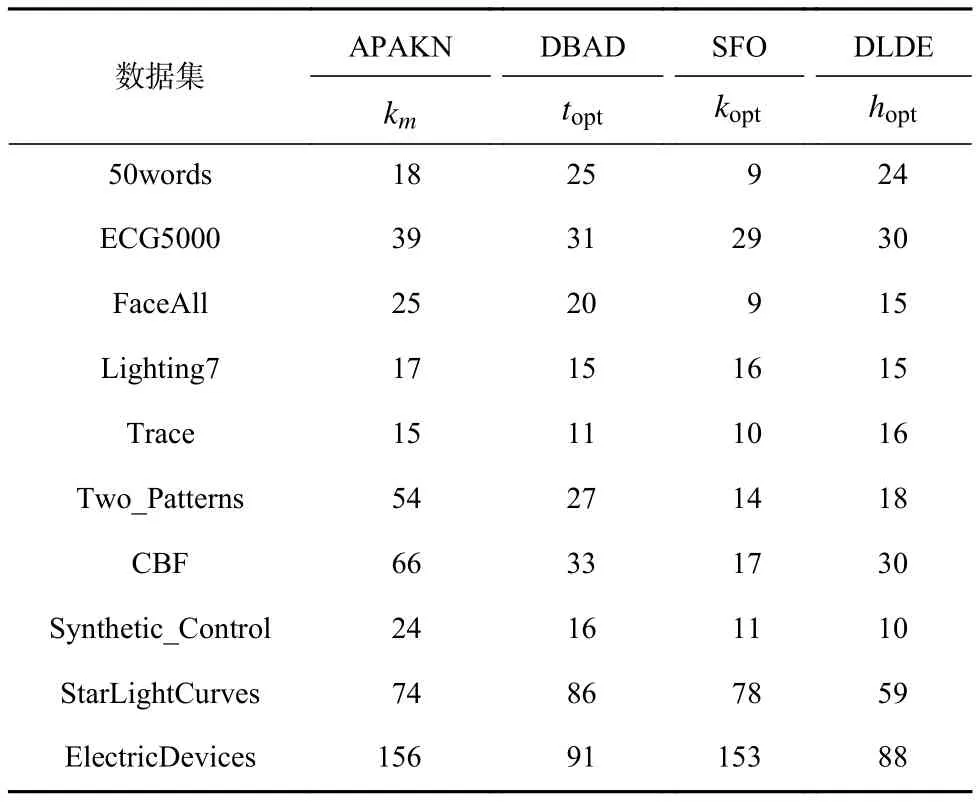
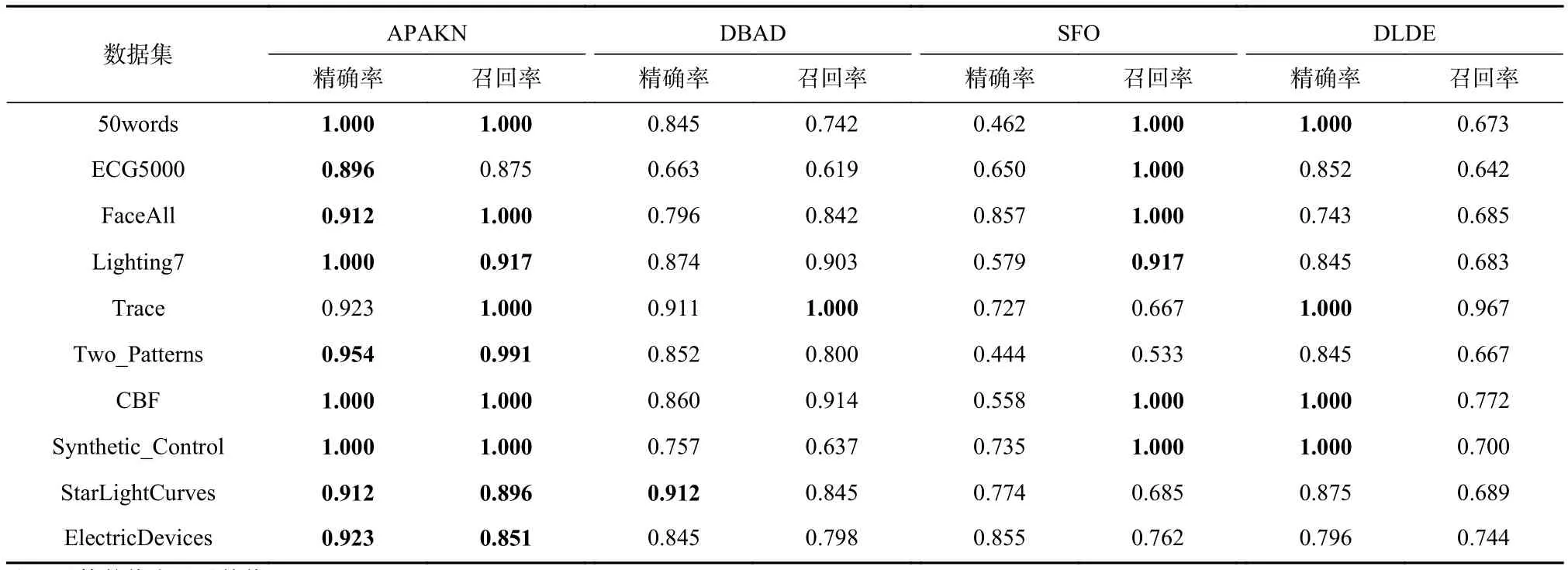
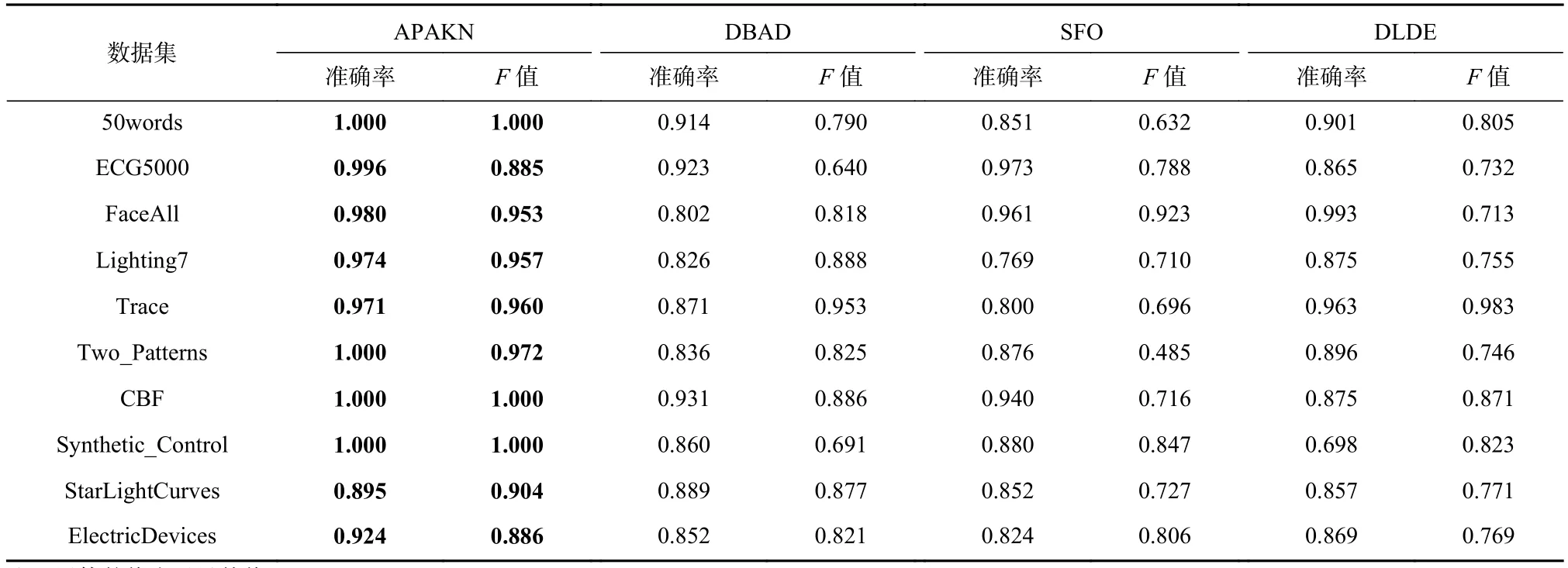
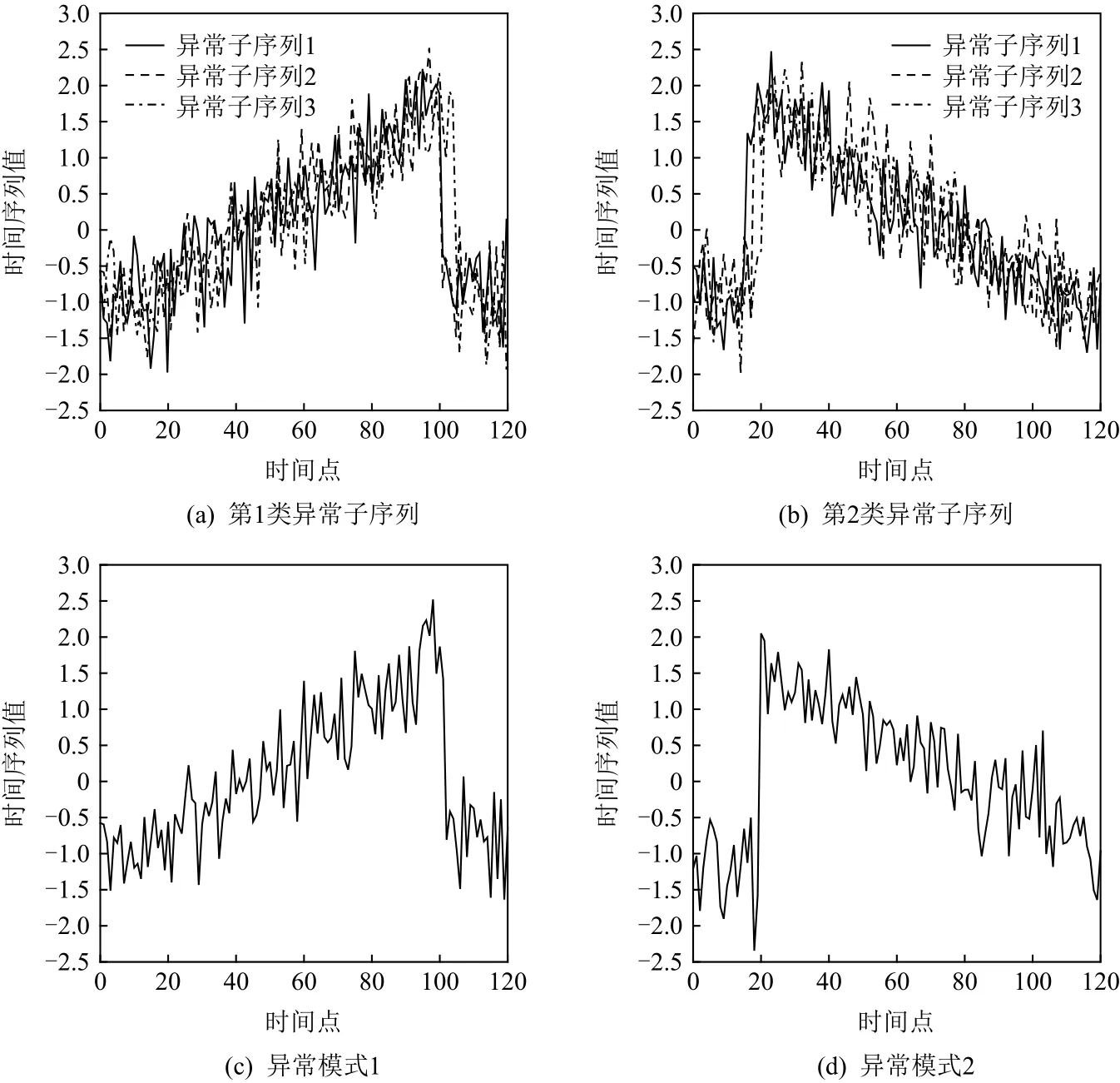
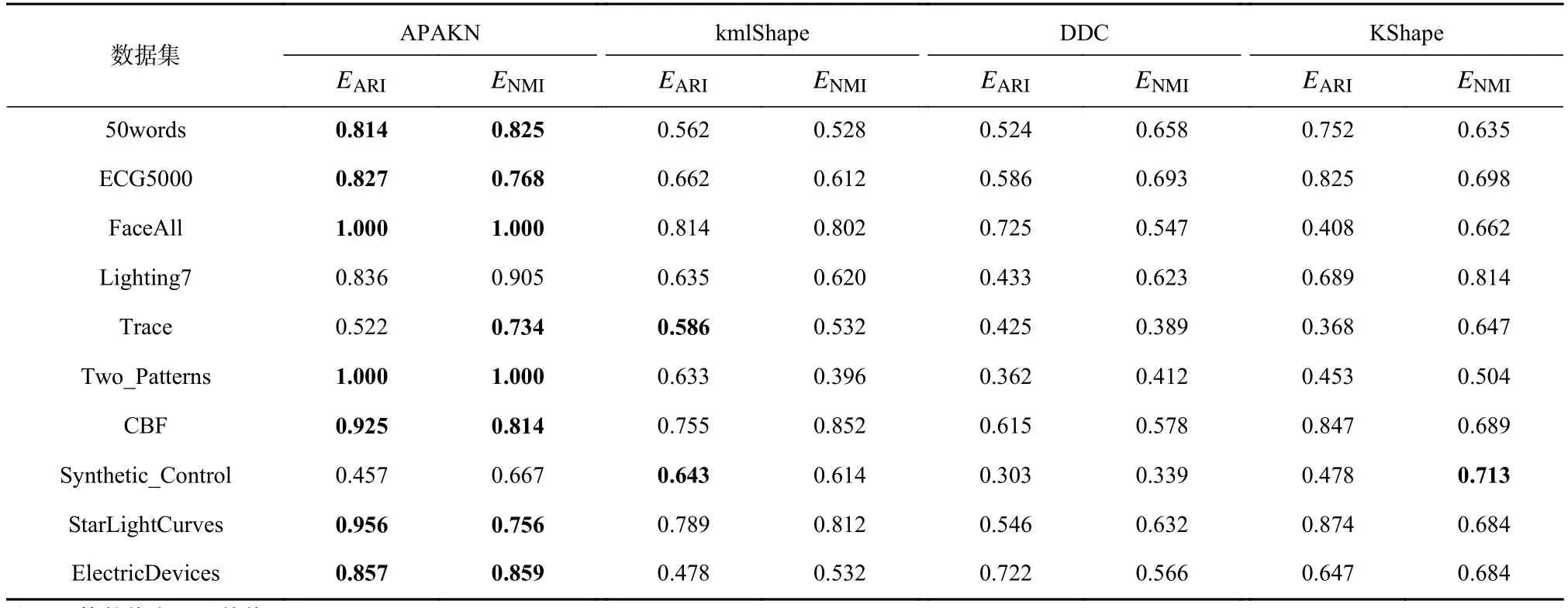
為了準確確定異常子序列,需要設置異常閾值T,將待檢測子序列si(i=1,2,…,N)的異常分數S′(si)與異常閾值T相比較.若S′(si) 其中均值u和標準差 σ 是確定值,令參數 β∈{0,0.1,0.2,0.3,…,2.8,2.9,3.0}.為了選擇合適的 β值確定最佳異常閾值T,以異常子序列和正常子序列的異常分數集合的方差之和作為目標函數,找出使得目標函數最小的 β以確定異常閾值T. 以圖1中子序列為例確定異常閾值T:所有子序列的異常分數的均值和標準差分別為0.280和0.315,β∈{0,0.1,0.2,0.3,…,2.8,2.9,3.0},則 異 常 閾 值T∈{0.280,0.312,0.343,0.375,…,1.162,1.194,1.225}, 根 據這31個閾值取值分別得到31種異常子序列集合,根據式(12)計算得出目標函數值的集合,當 β =0.3 時取得目標函數的最小值0.015,此時確定異常閾值T=0.280+0.315×0.3=0.375,由于只有S′(s1)≥T,則檢測出圖1中子序列s1為異常子序. 針對異常子序列的多樣性,為區分不同類型的異常子序列,本節對得到的異常子序列進行聚類,將每個聚類中心定義為一個異常模式,對不同的異常模式進行識別.本算法能夠在聚類個數未知的情況下保證聚類結果的有效性. APAKN根據2個條件尋找聚類中心:1)聚類中心的密度高于其鄰近的子序列的密度;2)任意2個類中心的距離相對較遠.首先利用2.1節描述的自適應k近鄰搜索算法確定所有異常子序列的自適應k近鄰值(i=1,2,…,n),將其作為各異常子序列的密度.將異常子序列中自適應k值最大的子序列作為第1個聚類中心p1,在與p1距離最遠的v個子序列中找出密度最大的異常子序列作為第2個聚類中心p2,其中即為異常子序列個數與10的比值取整加1.在距離存儲單元搜索剩余子序列與2個聚類中心之間的距離,確定聚類數為2時各子序列所屬聚類.同時使用輪廓系數 (silhouette coefficient)[29]作為聚類有效性指標計算當前的輪廓系數sil2. 當聚類數為q時,輪廓系數的計算公式為 其中N為所有子序列個數,Ci表 示第i個類簇,w為屬于類簇Ci的 子序列,sam(w,Ci)被稱為子序列w的簇內不相似度,是子序列w到同類其他子序列的平均距離,dif(w,Ci)被稱為子序列w的簇間不相似度, 是子序列w到所有其他簇的所有子序列的平均距離中最小的那一個.定義分別為: 其中nCi為 類別Ci所 包含 子序列的 個數,nCl為 類 別Cl所包含子序列的個數,ddtw(w,u)表示子序列w與u之間的DTW距離.輪廓系數的值越大,說明同類樣本相距越近,不同樣本相距越遠,聚類效果越好.使得有效性指標最大的聚類中心集合即是算法求得的所有聚類中心. 當聚類數為i時,在與已有聚類中心{p1,p2,…,pi?1}的距離之和最大的v個子序列中找出密度最大的異常子序列作為第i個聚類中心pi,把每個剩余異常子序列分配給距離其最近的聚類中心.計算此時的輪廓系數sili,若sili Fig.5 Schematic diagram of anomaly subsequence distribution圖5 異常子序列分布示意圖 算法 1.APAKN 算法. 輸入:子序列數據集D={s1,s2,…,si,…,sN}; 輸出:異常模式集合P={p1,p2,…,pi,…,pc}. 步驟1.對于數據集D={s1,s2,…,si,…,sN},計算所有子序列之間的DTW距離并將其存放在距離存儲單元中以便隨時調用,利用子序列距離搜索子序列si(i=1,2,…,N)的自適應k近鄰值. 步驟2.將k值集合 {k1,k2,…,kN}中的最大值km代入式(6)計算所有子序列的相對密度,計算異常分數和確定異常閾值,將異常分數大于異常閾值的子序列檢測為異常子序列 步驟3.重新搜索異常子序列s?的自適應k值j將其作為的密度,根據所得密度和距離存儲單元中的子序列距離迭代地獲取聚類中心,并根據式(13)中的輪廓系數判斷迭代停止時聚類中心的個數c. 步驟4.輸出聚類中心集合,即異常模式集合P={p1,p2,…,pi,…,pc}. APAKN算法采用DTW 度量所有子序列之間的距離,該步驟的最大時間復雜度為,其中數據集中子序列數為N, 所有子序列長度都為l;異常子序列檢測步驟的最大時間復雜度為其中km為所有子序列自適應k值集合中的最大值;異常子序列聚類步驟的最大時間復雜度為,其中,n為異常子序列的個數.可見,APAKN算法的時間復雜度為由于NlogN++nlogn?N2l2,算法的時間復雜度可以表示為 為了更好地驗證所提出算法的有效性,采用了美國加州大學濱河分校 (University of California Riverside,UCR)的時間序列數據集合[30]中的10個通用數據集作為實驗對象對本文算法進行實驗評估.由于APAKN算法主要是由異常子序列檢測和異常子序列聚類2個方面組成,因此實驗部分也將從這2個方向來進行評價.實驗環境均為 Win 10 64 b 操作系統,Python 3.7.6 軟件,8 GB 內存,Intel(R) Core(TM),i5-4200H CPU@2.80 GHz 處理器. 本次實驗所用數據為 10 個公開的UCR數據集,由于UCR數據集中并未標出各類子序列是否異常,所以我們選擇子序列個數最多的一類作為正常類,隨機選擇其他幾類中的若干子序列組成異常類,使各數據集的異常率不同.表3列出了本次實驗中各數據集的詳細信息.以50words數據集為例,原數據集包含50個類別,其中類別號為2的子序列簇包含最多的子序列且被選作正常類,類別號為4,10,43的子序列簇被選作異常類,從中隨機選擇若干子序列作為實驗中的異常子序列. Table 3 Experimental Data Sets表3 實驗數據集 3.2.1 評價指標 本節使用準確率(Accuracy)、精確率(Precision) 、召回率(Recall) 、F值作為性能評價指標來評價本算法中異常子序列檢測部分的性能,分別定義為: 其中,TP被定義為將異常子序列檢測為異常子序列的個數;FP為把非異常子序列檢測為異常子序列的個數;FN為將異常子序列檢測為非異常子序列的個數;TN表示將非異常子序列正確檢測為非異常子序列的個數. 準確率代表的是所有正確預測的樣本數占總樣本數的比重;精確率衡量算法的查準率,即正確預測為異常子序列占全部預測為異常子序列的比例;召回率衡量算法的查全率,即正確預測為一場子序列占全部實際為異常子序列的比例;F值則為精確率和召回率的調和平均數,同時兼顧算法的精確率和召回率,F度量值的大小反映了聚類結果的精度,它是一個介于?1和1之間的值,該值越接近1,算法的精度就越高. 3.2.2 實驗結果 為了證明APAKN算法的優異,圖6將算法異常子序列檢測部分在10個數據集上的部分實驗結果可視化地表示出來.圖6中共包含代表著10個數據集的10個子圖,每個子圖由2個部分組成:時間子序列和子序列異常分數.以50words數據集為例,該數據集的子序列長度為270,我們從類別號為4,10,43這3個異常子序列簇中分別選擇了3個子序列,從類別號為2的正常子序列簇中選擇若干子序列,將這些子序列的異常得分在圖6 (a)中顯示出來.如圖6 (a)所示,異常子序列的異常分數遠遠高于正常子序列的異常分數.此外,對數據集的其他子序列都分配了一個異常分數來度量它們的異常程度. 為了驗證提出的異常模式識別算法APAKN在異常子序列檢測部分的性能, 本文比較了APAKN與DBAD[13],SFO[15],DLDE[18]算法在各數據集的實驗結果.APAKN利用自適應k近鄰搜索算法自動確定各子序列的最佳近鄰值 {k1,k2,…,kN},km為近鄰集合中的最大值;異常子序列檢測部分的對比算法DBAD遞歸計算擬合分布均值方差,需要人為設置遞歸參數t;SFO需要人為設置近鄰參數k;DLDE構造Hash表以加快估計子序列的局部密度,需人為設置參數Hash值h.為了突出顯示本文算法的優越性能,在10個實驗數據集上,對3個對比算法分別進行多次實驗,最終選出一個使其對應檢測結果最優的參數值作為其最佳參數,分別記為topt,kopt,hopt.APAKN算法得到的自適應k值中的最大值km以及對比算法相應的topt,kopt,hopt如表4所示. Fig.6 UCR partial time subsequences and anomaly scores圖6 UCR部分時間子序列及其異常得分 此外,APAKN提出基于最小方差的自適應閾值方法確定異常閾值;SFO算法利用統計假設檢驗方法判斷數據是否異常,其計算較為復雜;而DLDE算法只是對所有數據對象按異常分數值降序排序,人為選擇異常分數值最大的幾個數據對象作為異常對象,該閾值選擇方法需要實驗者熟悉各數據集,并且對不同數據集進行實驗時需要置換閾值參數,使實驗過程更為繁瑣.DBAD利用均值和方差確定異常閾值,同樣需要人為設置閾值參數.本次實驗利用較為常見的 3 σ準則作為DBAD和DLDE算法的異常閾值T=u+3σ.基于表4的最佳參數,表5和表6分別給出了4種算法在異常子序列檢測部分的精確率和召回率以及準確率和F值. 表5給出了4種算法在10個數據集上異常子序列檢測的精確率和召回率對比,表6則給出了異常子序列檢測部分的準確率和F值對比, 可以看出,APAKN在10個數據集上的實驗結果皆具有最佳性能.此外,DBAD算法有1個最佳精確率和1個最佳召回率;SFO有6個最佳召回率;DLDE有4個最佳精確率.由上述實驗結果可以判斷出,相較于其他算法,本文算法不僅具有很強的自適應性,而且具有很高的異常子序列檢測水平. Table 4 km Value of APAKN and the Optimal Parameter Values of Comparison Algorithms表4 APAKN的 km 值和對比算法的最佳參數值 3.3.1 評價指標 本文利用調整蘭德系數 (adjusted rand index, ARI)[31]和標準化互信息 (normalized mutual information, NMI)[32]兩種衡量標準對異常子序列聚類結果進行評判.這2個衡量標準的上限均為1,該值越接近1,表示該聚類算法的準確率越高,算法聚類結果越好. Table 5 Comparison of Accuracy and Recall of Each Algorithm on 10 Data Sets表5 各算法在 10 個數據集上的精確率和召回率對比 Table 6 Comparison of Accuracy and F Value of Each Algorithm on 10 Data Sets表6 各算法在 10 個數據集上的準確率和F值對比 調整蘭德系數值EARI定義為 其中na表示在算法聚類結果中為同一類、在數據集真實聚類中也為同一類的子序列對數;nb表示在算法聚類結果中為同一類、在數據集真實聚類中不為同一類的子序列對數;nc表示在算法聚類結果中不為同一類、在數據集真實聚類中為同一類的子序列對數;nd表示在算法聚類結果中不為同一類、在數據集真實聚類中也不為同一類的子序列對數. 標準化互信息值ENMI定義為 其中cA表 示算法聚類結果的聚類類別數,cB表示數據集本質聚類類別數,nij表 示子序列屬于真實標簽類j但被劃分到聚類結果簇i中的個數,ni表示聚類結果類i中子序列的個數,nj表示真實標簽類j中子序列的個數. 3.3.2 實驗結果 為了證明APAKN算法的優異, 圖7和圖8分別將算法異常子序列聚類部分在50words和CBF數據集上的實驗結果可視化地表示出來.圖7包含代表著3類異常子序列的異常子序列示例和聚類算法下生成的簇質心即異常模式.通過圖7中不同類別下的異常子序列的示例可以看出,同一類別下的異常子序列具有相同的趨勢.從異常模式圖可以看出算法得到的質心很好地表征了每個類別的趨勢特征. 在異常子序列聚類部分,本文選擇了kmlShape[21],DDC[23],KShape[24]算法進行性能比較.APAKN的聚類部分同樣無需設置任何參數,而為了更好地顯示出算法的優異性,對3種對比算法都進行了參數調優.由于kmlShape算法選取的初始類簇中心不同,則聚類結果也不同,對每個數據集進行多次重復實驗, 取其中最好的結果.kmlShape,DDC,KShape算法需要給定類簇個數,為這3種算法分別選出一個使評價指標最優的參數作為其聚類個數.表7為APAKN的異常子序列聚類部分在10個UCR數據集上與kmlShape,DDC,KShape這3種算法的聚類結果對比. 通過表7可知,即使已經給定了對比算法的最佳參數,kmlShape,DDC,KShape算法的聚類結果還是波動較大, DDC聚類效果不佳.kmlShape算法在FaceAll,Trace,CBF,Synthetic_Control數據集上的性能值較優,在其他數據集上的表現不佳;KShape算法在 50words,ECG5000,Lighting7,CBF 數據集上表現較好.但從總體上來看,APAKN在各個數據集上的評價指標值大部分都要優于與之比較的算法,其余指標均值與最佳指標值相差不大. Fig.7 Examples of anomaly subsequences and anomaly patterns in different categories of the 50words dataset圖7 50words數據集在不同類別下的異常子序列示例和異常模式 Fig.8 Examples of anomaly subsequences and anomaly patterns in different categories of the CBF dataset圖8 CBF數據集在不同類別下的異常子序列示例和異常模式 Table 7 Comparison of ARI and NMI of Each Algorithm on 10 Data Sets表7 各算法在 10 個數據集上的ARI和NMI對比 因此,結合異常子序列檢測與異常子序列聚類2部分的實驗結果, 可以驗證出算法APAKN是有效可行的. 本文提出了基于自適應k近鄰的異常模式識別算法APAKN,該算法在無需任何參數輸入的情況下,不僅檢測異常子序列,還區分出異常子序列的不同類別,重新定義了異常模式.采用自適應k近鄰搜索算法獲取子序列的自適應k近鄰值,解決傳統k近鄰算法的參數設置問題;提出一種基于最小方差的自適應閾值方法解決閾值選擇問題;APAKN通過密度與距離結合的思想尋找最優聚類中心,并利用輪廓系數得到聚類數,從而實現異常子序列的快速聚類.在UCR數據集上的實驗結果表明了APAKN算法的自適應性與有效性.下一階段我們將考慮如何從距離度量方面減少算法的時間復雜度以期望提高算法的效率. 作者貢獻聲明:王玲提出文章的算法思路設計,對論文的邏輯性以及算法的合理性進行指導;周南負責文章的定理和論證過程,以及實驗部分的算法實現與實驗結果分析;申鵬對文章整體格式進行修改.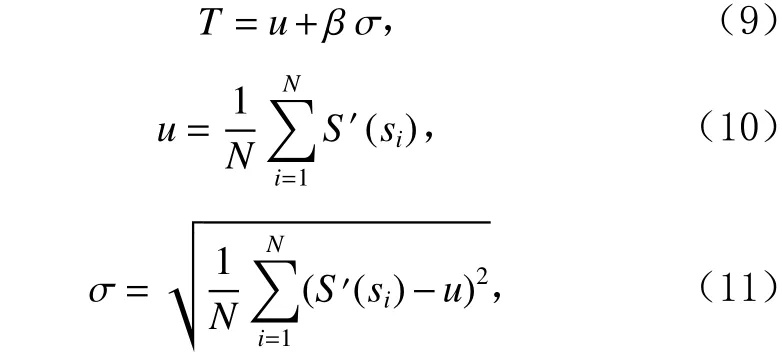
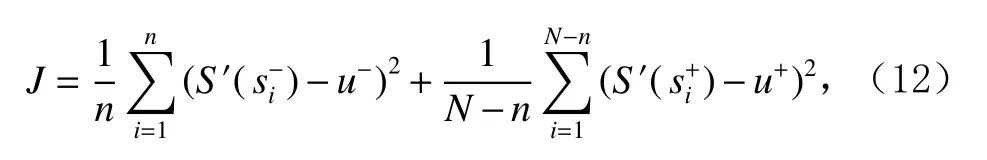
2.2 基于自適應 k 近鄰的異常子序列聚類
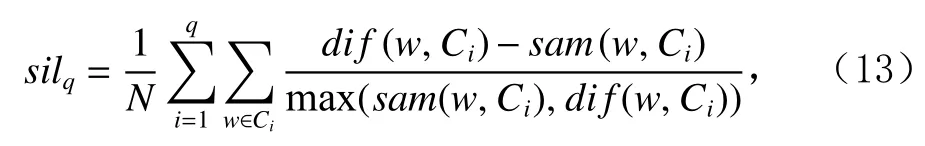
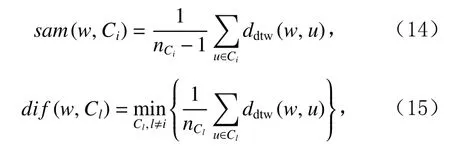
2.3 APAKN算法步驟
2.4 時間復雜度
3 實驗與結果
3.1 實驗數據
3.2 異常子序列檢測
3.3 異常子序列聚類
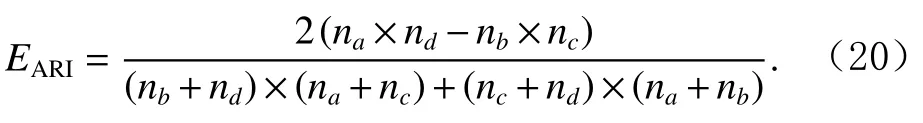

4 結 論

