基于深度展開的大規模MIMO 系統CSI 反饋算法

廖勇，程港，李玉杰

（重慶大學微電子與通信工程學院，重慶 400044）

0 引言

大規模多輸入多輸出（MIMO,multiple input multiple output）技術憑借其高能量效率、高頻譜效率和大系統容量等優勢成為下一代移動通信的關鍵技術之一[1]。為了充分利用大規模MIMO 技術帶來的潛在性能增益，基站需要獲取足夠精確的下行鏈路信道狀態信息（CSI,channel state information）[2]。在時分雙工（TDD,time division duplex）大規模MIMO 系統中，可以利用上下行信道的互易性來獲得CSI。但是在頻分雙工（FDD,frequency division duplexing）大規模MIMO 系統中，用戶必須先估計下行鏈路CSI，再通過上行鏈路反饋回基站[3]。由于大規模MIMO CSI 矩陣具備角度時延域稀疏特性，壓縮感知[4]可以被應用于CSI 反饋。雖然壓縮感知理論與大規模MIMO 的CSI 反饋模型比較貼合，但目前依然存在一些技術挑戰，因此研究人員開始關注深度學習在CSI 領域的應用。文獻[5]提出了第一個FDD 大規模MIMO 的CSI 反饋網絡CsiNet，它是一種通過引入自編碼器結構[6]，并且模擬壓縮感知框架構建的高反饋精度的網絡，相比于傳統的壓縮感知方法，有較好的反饋性能和更低的復雜度。為了進一步提升網絡的恢復效果，文獻[7]在CsiNet 的基礎上提出了CsiNet+，該網絡在用戶設備處利用更大卷積核的卷積層增加CSI 矩陣的感受野，提取更多的深層次特征，在基站處利用更多的卷積網絡提高CSI 重構精度。針對快時變FDD大規模MIMO 系統中因多普勒頻移導致的信道時間相關性使系統無法保證高可靠和低時延通信的問題，文獻[8]利用卷積神經網絡（CNN,convolutional neural network）和批標準化網絡對CSI 矩陣中的噪聲進行提取并且學習信道的空間結構，通過注意力機制提取CSI 矩陣間的時間相關性以提高CSI 重構的精度。在高速移動環境下，信道特征復雜多變，同時存在加性噪聲和非線性效應的影響，文獻[9]提出一種殘差混合網絡，可消除高速移動場景加性噪聲的影響，學習并適應稀疏、雙選衰落信道特征，在高壓縮率與低信噪比條件下依然具有較好的性能表現。針對FDD 模式下CSI 反饋方法復雜度高、精度低和開銷大的問題，文獻[10]提出了一種輕量化低復雜度的反饋方法，該方法在時間復雜度和空間復雜度上均有良好的表現。

值得注意的是，大多數的深度學習方法需要依靠大量已分類標記的數據來進行神經網絡的訓練，因此這種方法也被稱為基于數據驅動的深度學習方法，但該方法不具備可解釋性。針對上述問題，研究人員發現將傳統的經典非線性迭代算法與深度學習的網絡參數訓練相結合，可以減小對大量標記數據的強依賴性，同時具備一定的理論保障和性能下限。這種通過結合經典非線性迭代算法的可解釋性和深度學習高性能的方法被稱作“深度展開”[11]。文獻[12]提出一種多任務神經網絡結構，通過展開基于最小均方誤差準則的兩次迭代來恢復下行鏈路的CSI 和上行用戶的數據序列，在減少上行鏈路帶寬資源占用方面表現優異。文獻[13]提出基于深度卷積神經網絡的馬爾可夫模型對前向CSI 進行差分編碼，能有效提高CSI 重構精度。文獻[14]將快速迭代收縮閾值算法（FISTA,fast iterative shrinkage thresholding algorithm）展開為FISTA-Net 并且作為大規模MIMO的CSI反饋算法，獲得了優異的性能。

針對基于深度學習的CSI 反饋算法存在待訓練參數過多、可解釋性不強的問題，本文提出了2 種基于深度展開的CSI 反饋算法，以近似消息傳遞（AMP,approximate message passing）[15]作為深度展開的基準算法，從2 個視角分別展開得到了基于可學習參數的 AMP（LP-AMP,learnable parameters-AMP）算法和基于卷積網絡的AMP（CNN-AMP,convolutional neural network-AMP）算法。本文的主要貢獻如下：1) LP-AMP 算法通過改進AMP 中的閾值函數和Onsager 項來解決CSI 矩陣非嚴格稀疏的問題；2) 隨著這種非嚴格稀疏性的加強，在LP-AMP 算法的基礎上提出了利用卷積殘差學習網絡改進閾值函數模塊的 CNN-AMP 算法，與LP-AMP 相比，CNN-AMP 在犧牲了一些復雜度的情況下，獲得了更加明顯的重構效果；3) 所提的基于深度展開的CSI 反饋算法既具有壓縮感知算法的可解釋性理論保障，又具有深度學習方法的高性能表現，可以為FDD 大規模MIMO CSI 反饋領域的研究提供一些可行的思路。

1 系統模型

本文針對單小區大規模MIMO 的通信系統，基站配備有Nt根發射天線，天線陣列方式采用均勻線性陣列，用戶端配備有單根接收天線。采用正交頻分復用系統，并有Ns個子載波，因此接收向量y可以建模為

其中，y是維度為Ns×1 的復數接收向量；x是Ns×1的復數發射向量；n是Ns×1的加性高斯白噪聲向量；是Ns×Nt的復數CSI 信道矩陣，其中行向量為每個子載波下的空域信道矢量，列向量為頻域信道矢量；U是Nt×Ns的復數預編碼矩陣。如果以空頻域矩陣作為反饋矩陣的基準，那么CSI 矩陣就是，此時的反饋總量是NsNt，這會占據大量的系統資源，因此需要設計低復雜度高反饋精度的有限CSI 反饋方法。

考慮到CSI 矩陣具備角度時延域的稀疏特性，為了降低CSI 的反饋開銷，將角度和時延域的稀疏特性全部應用于空頻域矩陣，經過兩次矩陣乘積的離散傅里葉變換（DFT,discrete Fourier transform），即可得到角度時延域稀疏CSI 矩陣為

將上述經DFT 稀疏和截斷之后的CSI 矩陣H作為待反饋矩陣，深度展開CSI 反饋模型如圖1 所示。首先，將用戶端估計得到的CSI 矩陣H經向量化和拼接得到長度為N=的實數稀疏向量x，在得到稀疏的待反饋向量x之后，測量矩陣使用獨立同分布高斯隨機矩陣A進行壓縮。將矩陣的壓縮和重構2 個過程分別使用編碼器和解碼器進行描述，編碼器在用戶設備處，解碼器在基站處。編碼過程表示為

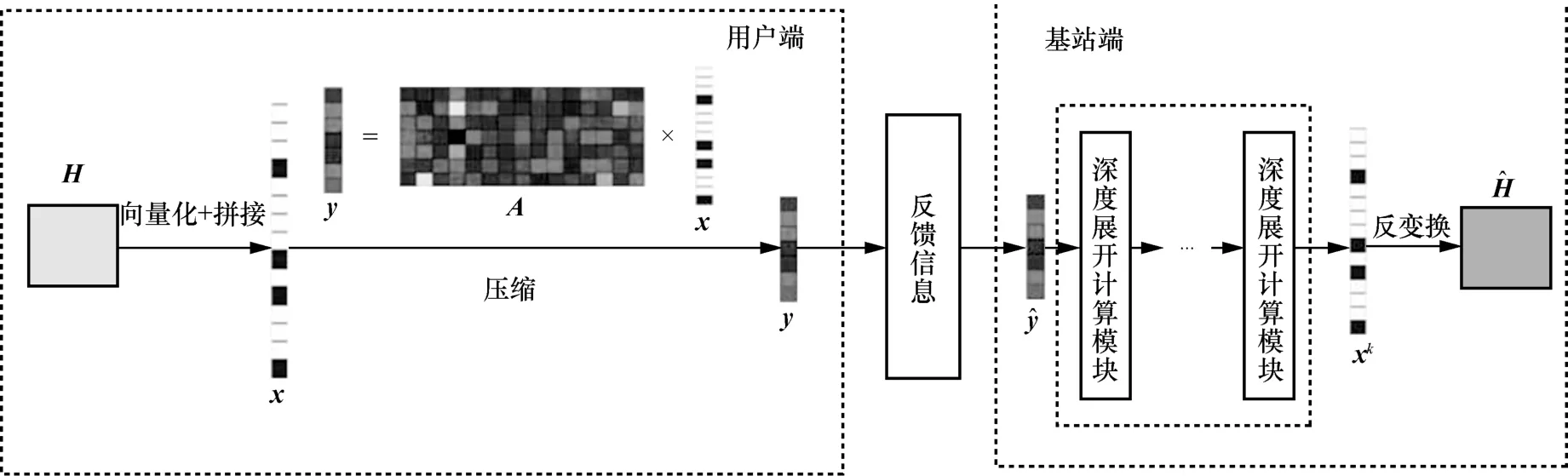
圖1 深度展開CSI 反饋模型

其中，y表示長度為M的測量向量，fen(·) 表示編碼器函數，Re(·) 表示取向量的實部，Im(·) 表示取向量的虛部，vec(·) 表示向量化操作。

y通過反饋信道到達基站，為了便于區分，以表示基站端接收到的測量向量，基站通過深度展開的AMP 算法恢復為第k次迭代的重構向量xk，然后反變換回CSI 稀疏矩陣，即可完成CSI 的反饋流程。解碼過程表示為

其中，fde(·) 表示解碼器函數。最終的訓練過程是將fen(·) 和fde(·) 聯立在一起進行端到端的訓練，這種端到端的訓練過程可表示為

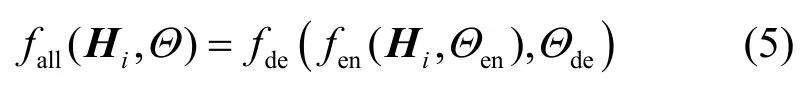
其中，fall(·) 是編碼器和解碼器聯立后的變換函數，Θ={Θen,Θde}是網絡的參數集合，Θen是編碼器參數，Θde是解碼器參數，Hi是第i例訓練樣本。

2 基于AMP 的深度展開CSI 反饋

2.1 深度展開的原理

深度展開模型由多個計算模塊組成，每個計算模塊對應非線性迭代算法中的一次迭代。文獻[16]指出，將深度學習方法與現有通信領域中的經典非線性迭代算法結合已成為近年來的研究熱點，并且已經應用到預編碼、信號檢測和信道解碼等處理中。深度展開模型架構如圖2 所示。

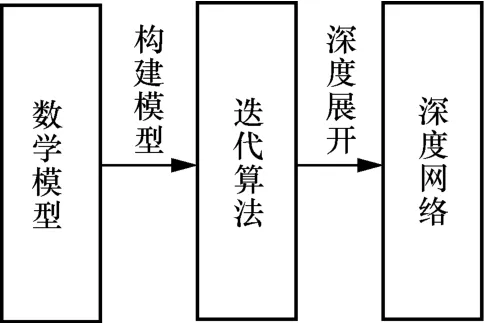
圖2 深度展開模型架構

深度展開模型包括3 個部分，即數學模型、迭代算法和深度網絡。在應用中將具體的實際問題抽象為數學模型，根據相關的數學理論推導得到具體的迭代算法，將迭代算法每輪迭代的計算式展開為深度網絡中的一層，利用可學習參數或神經網絡替換原始迭代算法中每輪迭代中的超參數或某個計算模塊。

2.2 AMP 算法

AMP 算法[15]很好地繼承了迭代閾值算法的優勢，又融入了消息傳遞算法的精髓。假設初始化重構向量x0=ATy，殘差向量z-1=y，第t（t≥ 0）次迭代可表示為

其中，u為軟閾值函數的輸入。

根據文獻[17]，Onsager 校正項中的bt與閾值λt為

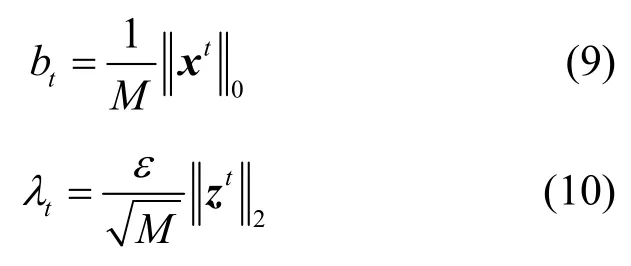
其中，ε是一個與稀疏度和測量向量長度M有關的可調數值。AMP 算法與FISTA 相似，不同之處在于AMP 算法在殘差向量更新時增加了Onsager 校正項，并且迭代閾值在每輪迭代中都會通過殘差向量和測量向量長度M進行調整。AMP 計算模塊如圖3 所示。

圖3 AMP 計算模塊

圖3 展示了AMP 算法迭代式中的每一個計算模塊，AMP 算法的流程如算法1 所示。

算法1AMP 算法

輸入測量向量y，高斯隨機矩陣A

輸出重構向量xt+1

初始化重構向量x0=ATy，殘差向量z-1=y，迭代次數t=1

步驟3t=t+1，若t＜N，返回步驟1，若t=N，迭代結束；

2.3 基于可學習參數的AMP 算法

本節對基于可學習參數的 AMP 反饋算法LP-AMP 的展開結構進行描述。具體而言，通過引入深度學習中梯度下降法更新網絡參數，優化AMP算法中的迭代更新參數，將算法的每輪迭代展開為深度網絡中的一層，再將多個這樣的層堆疊，在模型訓練的過程中逐漸優化每層中不同的可學習參數，使模型以更少的迭代層數更快地收斂。LP-AMP的中間展開計算模塊如圖4 所示。

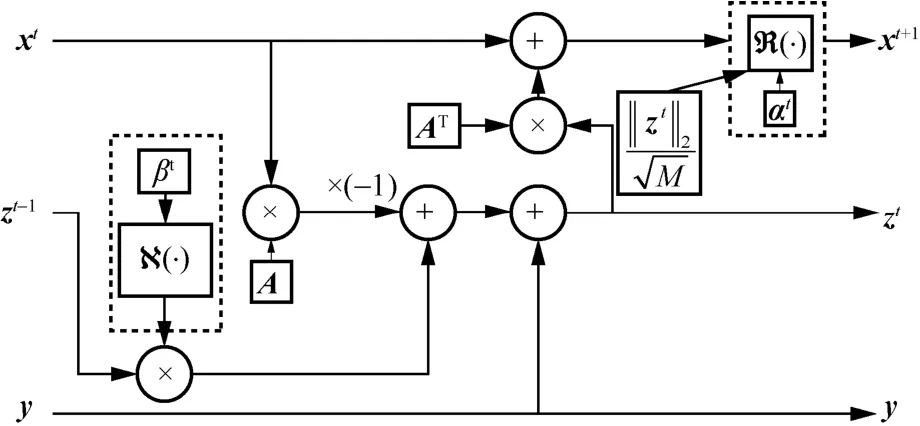
圖4 LP-AMP 的中間展開計算模塊

輸入層對進入迭代中的x t和z t進行初始化操作，輸出層將迭代至最后的x k作為LP-AMP 的最后輸出，中間展開計算模塊的 R(·) 和 N(·) 函數是引入可學習參數α t向量和β t參數的2 個可學習模塊。LP-AMP 算法的初始化和中間展開式可以表示為

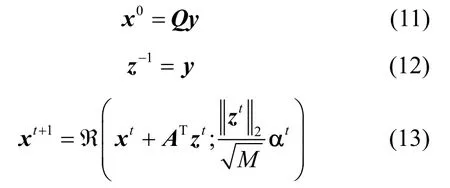
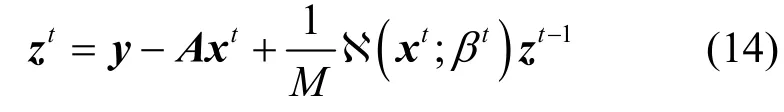
其中，x0的初始化是通過將采樣矩陣的轉置AT作為可學習矩陣Q的初始化，在不斷訓練的過程中，調整矩陣Q的分布，增強初始重構效果；α t是第t層展開中的可學習向量；β t是第t層展開中的可學習參數。對于展開式中的 R(·) 和 N(·) 模塊，R(·) 模塊對應原始AMP 算法中的閾值函數η(·) 部分，與閾值函數有所不同；N(·) 模塊則對應于Onsager 項部分中的對x t的0 范數計算過程。

閾值函數η(·) 和 R(·) 模塊的對比如圖5 所示。

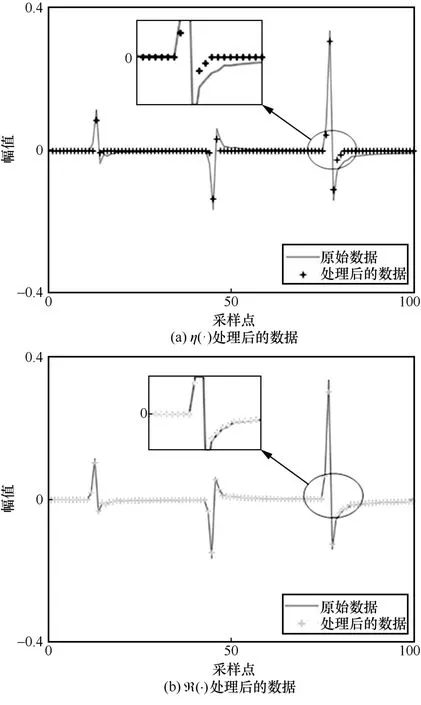
圖5 閾值函數 η (·) 和 R(·) 模塊的對比

從圖5 可以看出，原始的CSI 數據并非嚴格稀疏，大多數的數據非常接近0，但是并不為0。閾值函數η(·) 則在一次更新迭代的情況下將絕對值小于閾值λt的參數嚴格置0，這破壞了原始信號的細節（即小于閾值但不為0 的點在重構信號中被刪除）。本文將原始的閾值函數η(·) 替換成 R(·) 計算模塊，是為了加強閾值函數在應對非嚴格稀疏數據時的非線性表征能力。與η(·) 閾值函數不同的是，R (·) 模塊引入可學習向量αt來提升整體的變換效果，計算式為

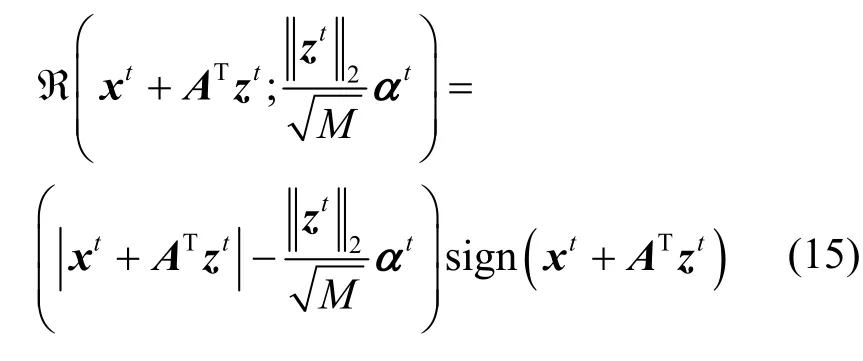
其中，α t∈RN是長度為N的可學習參數向量，它的長度與重構向量x t的長度相同，即N=。R(·) 模塊的計算式使不會有小于閾值的點被嚴格置0，并且每個數據點都有一個可學習參數進行調整。

N(·) 模塊對應于AMP 算法中Onsager 中求解x t的0 范數部分，x t的0 范數是指向量x t中的非零元素的數目。但是通過 R(·) 模塊處理后的數據幾乎不存在嚴格為0 的數據，因此 N(·) 模塊中對0 范數的處理同樣需要通過可學習參數來模擬。具體而言，將可學習參數βt作為計算非零元素數目的閾值，超過βt閾值的數據點被判定為非零元素。通過后續的仿真實驗可以看到，引入可學習參數βt可以減少算法的總迭代次數并提高重構精度。另外，值得注意的是，采樣矩陣A是服從高斯分布的隨機矩陣。然而，已有研究證明，設計合理的采樣矩陣可以提高CSI 矩陣重構的精度[18]。在LP-AMP 中也不例外，為了提高重構精度，利用經訓練過后的A進行數據的壓縮，Q進行數據的初始重構。LP-AMP算法的流程如算法2 所示。

算法2LP-AMP 算法

輸入測量向量y，訓練后的矩陣A

輸出重構向量xt+1

初始化重構向量x0=Qy，訓練后的矩陣Q的初始化為AT，殘差向量z-1=y，迭代次數t=1

步驟1由測量向量y、訓練后的矩陣A、當次迭代的xt、當前展開計算模塊中的可學習參數β t、前一次迭代的z t-1計算出當次迭代的z t=y-Ax t+M-1N（x t;βt）z t-1；

步驟2引入可學習參數αt向量，利用當前展開計算模塊中的R(·) 計算得到

步驟3t=t+1，若t＜N，返回步驟1，若t=N，迭代結束；

2.4 基于卷積網絡的AMP 算法

LP-AMP 的 R(·) 閾值模塊依然面臨一個重要的問題，即雖然LP-AMP 通過可學習參數作為每層的閾值向量，但是在訓練之后會使 R(·) 模塊中的閾值向量α t成為固定值，這會使個別不符合總體樣本特征的數據重構效果變差，進而影響算法的整體泛化能力。在LP-AMP 的整個流程中，R(·) 模塊幾乎承擔著大部分的非線性計算過程，而深度學習中CNN在應對非線性表征時，往往有著更好的性能。因此本節利用卷積殘差學習模塊替換LP-AMP中的閾值模塊 R(·)，其余部分不做任何改動。為了方便后續的描述，將基于卷積殘差學習網絡的AMP 反饋算法命名為 CNN-AMP。從理論推導角度而言，LP-AMP 中 R(·) 的作用是去除數據中的高斯白噪聲影響。具體的推導過程如下。

根據y=Ax可得

根據上述推導，AMP 算法中η(·) 閾值函數的作用是去除每輪迭代重構信號中的高斯白噪聲。CNN-AMP 的中間展開計算模塊如圖6 所示，其與LP-AMP 的不同之處僅在于將 R(·) 模塊替換為了?(·) 模塊，?(·) 模塊由3 個深度可分離卷積層[19]構成，卷積核的大小為3×3，每個卷積層之間通過ReLU 激活函數相連。值得強調的是，?(·) 模塊利用殘差學習[20]的模式，將網絡的輸入減去網絡的輸出得到最終結果，即 ?(·) 模塊將學習到每輪重構向量的高斯白噪聲，最后通過輸入減去噪聲得到該展開層信號的重構。

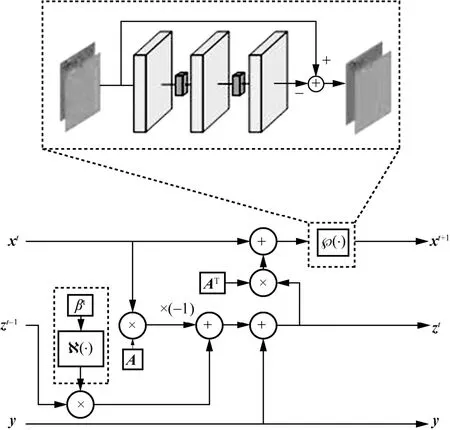
圖6 CNN-AMP 的中間展開計算模塊

根據上述對CNN-AMP 的描述，它的迭代展開式可以寫為

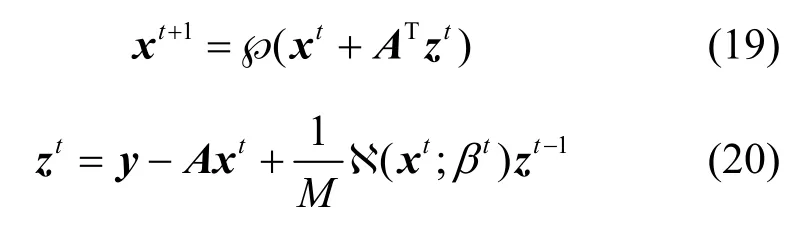
其中，CNN-AMP 中的 (Nxt;βt) 模塊與LP-AMP保持一致，依然利用學習參數 βt作為模擬求解xt的0 范數閾值。CNN-AMP 的輸入層的初始化過程以及輸出層也與LP-AMP 保持一致，為了提高重構精度，采樣矩陣A與初始重構矩陣Q同樣加入網絡參數的訓練。CNN-AMP 算法的流程如算法3 所示。

算法3CNN-AMP 算法

輸入測量向量y，訓練后的矩陣A

輸出重構向量xt+1

初始化重構向量x0=Qy，訓練后的矩陣Q的初始化為AT，殘差向量z-1=y，迭代次數t=1

步驟1由測量向量y、訓練后的矩陣A、當次迭代的x t、當前展開計算模塊中的可學習參數β t、前一次迭代的z t-1計算出當次迭代的z t=y-Axt+M-1N(x t;βt)z t-1；

步驟2引入殘差學習模塊 ?(·)，利用當前展開計算模塊中的 ?(·) 計算得到x t+1=?(x t+ATz t)；

步驟3t=t+1，若t＜N，返回步驟1，若t=N，迭代結束；

3 模型訓練與復雜度分析

3.1 模型訓練

對比LP-AMP、CNN-AMP 和AMP 的展開或迭代式可以發現，若去掉LP-AMP 和CNN-AMP中的 R(·)、N (·) 和 ?(·) 模塊，將其更改為原始閾值函數η(·) 和常規的 0 范數計算，LP-AMP 和CNN-AMP 就會退化為AMP 算法，也就是說，LP-AMP 和CNN-AMP 的性能下限是可以預知的，即存在理論前提和性能保障。但是基于數據驅動的深度學習方法的性能則無法提前預知，在進行訓練之前，無法保證得到很好的效果。為了方便后續對比實驗的分析，這里k1層展開的LP-AMP和k2層展開的CNN-AMP 被命名為LP-AMP-k1和CNN-AMP-k2。產生數據集的信道模型是基于空間幾何的隨機信道模型 COST2100[21]，其在COST259 模型和COST273 模型的基礎上進行構建，可以在時間、頻率和空間上重現MIMO 信道的隨機屬性。產生的數據集分別為100 000 訓練集、30 000 驗證集和20 000 測試集。采用端到端的訓練方式，訓練的損失函數采用均方誤差（MSE,mean square error），它是一種計算預測值和真實值之間誤差的函數，具體的表達式為

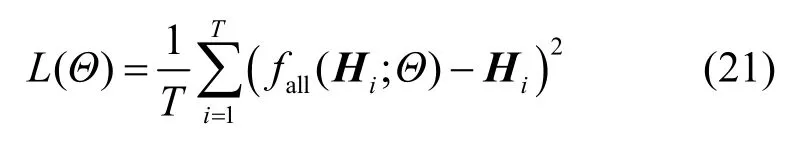
其中，Hi為原始輸入的第i例樣本，矩陣的維度是32×32，Θ為網絡中的所有參數，包括A、Q、α t、β t等，fall(·) 為整個網絡的計算式，fall(Hi;Θ)為恢復的第i例樣本，T為總的訓練樣本數量。優化器算法為自適應矩估計[22]優化器，它是隨機梯度下降算法的一種變體。采樣矩陣A使用服從高斯分布的隨機矩陣初始化填充，第t層可訓練向量α t使用0.1 初始化填充，第t層β t也初始化為0.1。

為了得到理想效果并避免梯度消失的問題，初始學習率設置為0.001，衰減率設置為0.9。使用的訓練設備配置為NVIDIA GeForce RTX 2080 Ti 顯卡，Intel Xeon E5-2678 v3 處理器，64 GB 內存。通過實驗發現，LP-AMP-k1的收斂速度比CNN-AMP-k2快得多。當壓縮率，批量數據大小為200，k1和k2分別取3 和7 時，LP-AMP-k1和CNN-AMP-k2的MSE 如表1 所示，采用Python平臺的深度學習框架Pytorch 搭建整體結構。

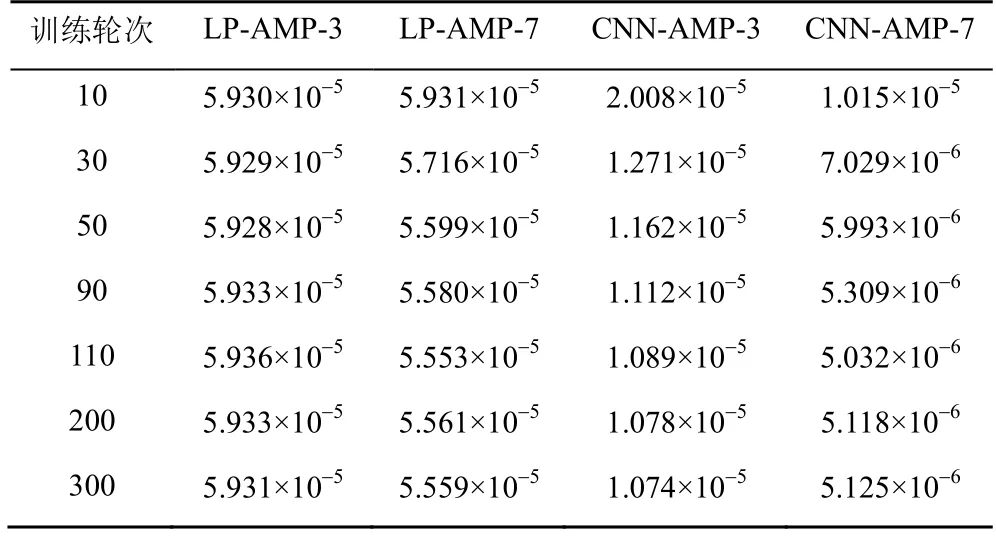
表1 LP-AMP-k1 和CNN-AMP-k2 的MSE

除此之外，還需要確定AMP 算法的收斂迭代次數，及LP-AMP-k1和CNN-AMP-k2的最佳展開層數。當室內場景下壓縮率時，LP-AMP-k1和CNN-AMP-k2在驗證集上的MSE如圖7 所示。從圖7 可以看出，當k1=1、3、5、7、9 時，LP-AMP-k1整體損失呈下降趨勢，但是損失整體相差并不大，隨著k1的增大，最終收斂的迭代次數開始增加，k1=3 和k1=5 時的收斂速度幾乎相同，k1=5 時的整體損失僅略低于k1=3。綜合復雜度和性能平衡之下，設置k1=3。另外，CNN-AMP-k2整體的損失比LP-AMP-k1低一個數量級，這也是在犧牲一些復雜度之下換取的性能優勢。隨著層數的增加，CNN-AMP-k2損失同樣呈下降趨勢，k2=5 和k2=7 時的損失差距不大，為了平衡復雜度和性能，設置k2=5。

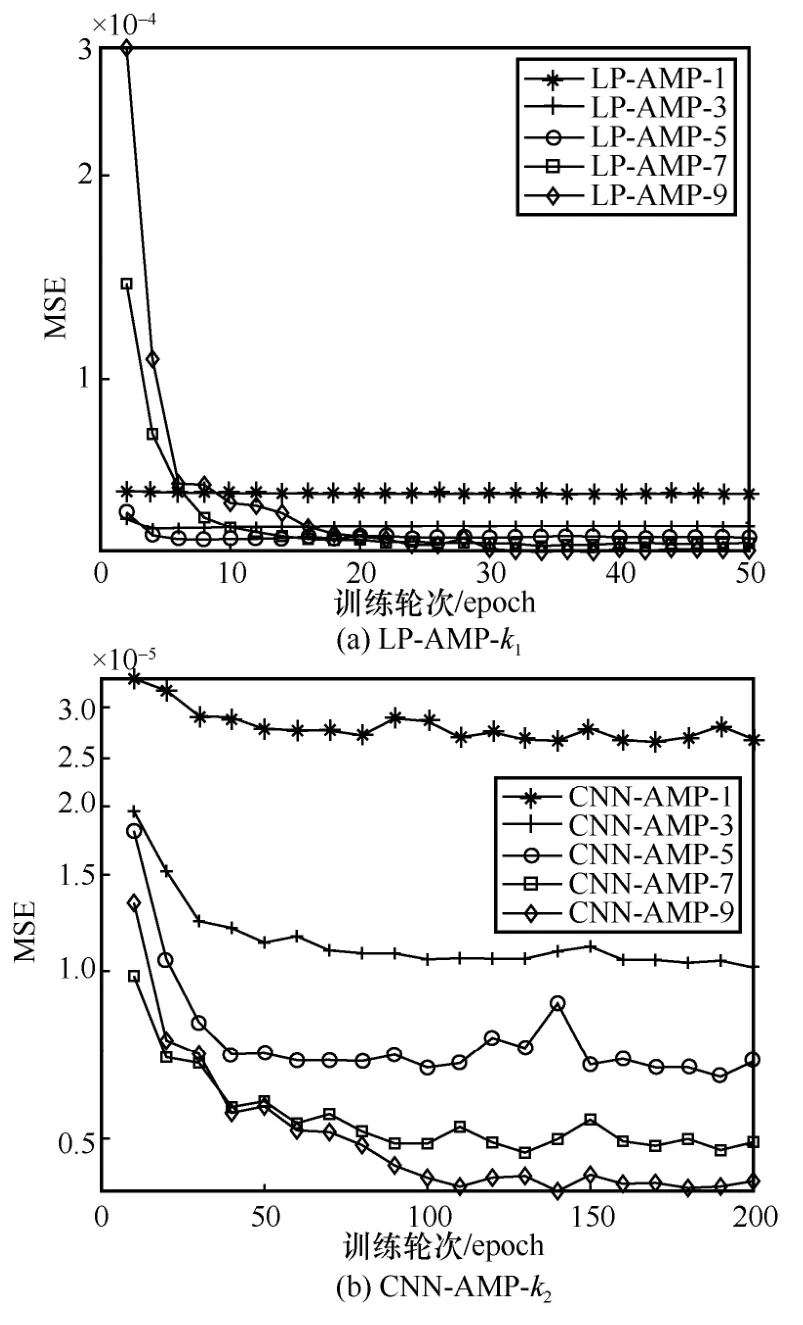
圖7 LP-AMP-k1 和CNN-AMP-k2 在驗證集上的MSE

AMP 的迭代次數q也是影響整體復雜度的關鍵參數，MSE 隨迭代次數的變化如圖8 所示。無論在室內或室外場景，AMP 算法信道矩陣的非嚴格稀疏性導致算法在驗證集上整體收斂于迭代次數50～100，以下的計算選取q=100。相比于LP-AMP-3，AMP 的乘法次數高一個數量級，與CNN-AMP-5較接近。

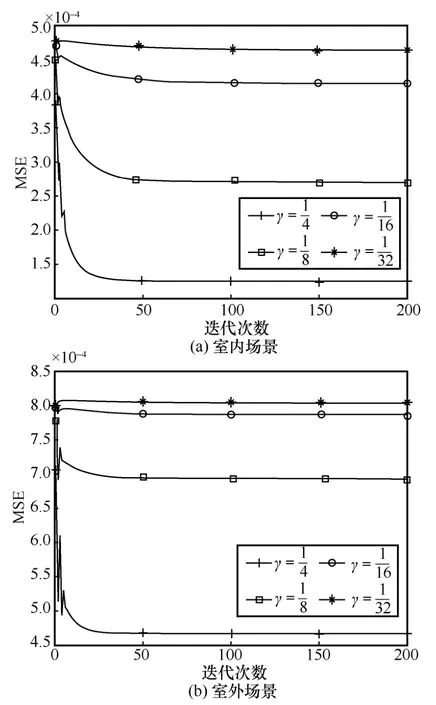
圖8 MSE 隨迭代次數的變化

3.2 復雜度分析

本節將通過對比 CsiNet、CsiNetPlus、LP-AMP-3、CNN-AMP-5 和AMP 方法來說明深度展開方法的優勢和缺陷，通過分析網絡的參數量和實數乘法次數來反映復雜度。對于網絡參數，AMP作為傳統的壓縮感知算法并不存在網絡參數，但是LP-AMP-3 和CNN-AMP-5 是AMP 的深度展開算法，引入了可學習參數和殘差學習模塊，需要計算整體的參數量。

參數量的計算將M=512、256、128、64 和N=2048代入計算，并且忽略所有結構的偏置項。不同算法編碼器和解碼器的參數量如表2 所示。

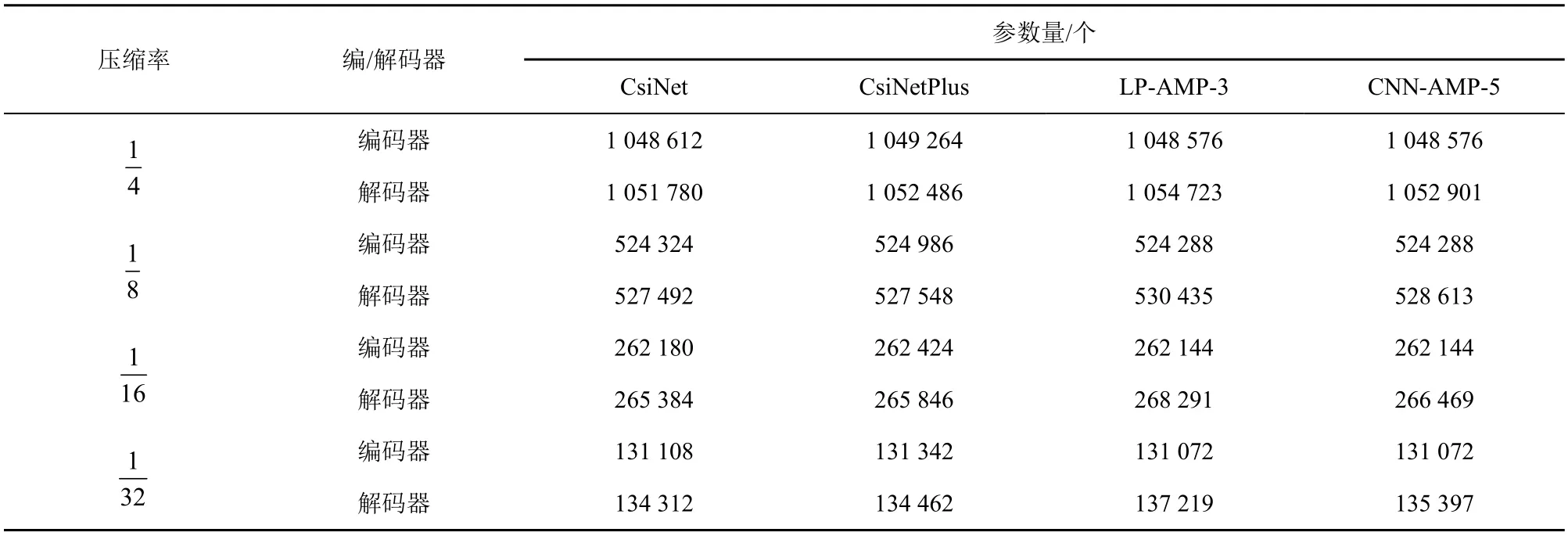
表2 不同算法編碼器和解碼器的參數量

LP-AMP-3 和CNN-AMP-5 算法編碼器部分的參數量與CsiNet 和CsiNetPlus 幾乎相同，這是因為LP-AMP-3 和CNN-AMP-5 都將采樣矩陣A作為可訓練參數，這與全連接神經網絡的壓縮過程在參數量的計算上是等價的。

在解碼器部分，LP-AMP-3 和CNN-AMP-5 比CsiNet 和CsiNetPlus 的參數量略大，不過總體來說，M×N依然是參數量計算的主體部分，數量級依然相同。LP-AMP-3 存在可訓練矩陣Q以及 R(·)、N (·) 模塊中的向量α t和參數β t，CNN-AMP-5 與LP-AMP-3 同樣存在可訓練矩陣Q，不同之處在于，R(·) 模塊被替換為 ?(·) 模塊，當層數越大時，參數量相應也就越大。

不同算法的乘法次數如表3 所示。AMP、LP-AMP-3 和CNN-AMP-5 在編碼器部分的乘法次數一樣，這是因為在壓縮感知算法的框架中，編碼器部分都是采樣矩陣A與待壓縮向量x的乘積，而所提算法和CsiNet 和CsiNetPlus 的乘法次數幾乎相同，這是因為它們的計算量主要來源于M×N。在解碼器部分，LP-AMP-3 在壓縮率為時比CsiNet 和CsiNetPlus 的乘法次數多，在其他壓縮率時則相反，這是因為所提算法的計算量不僅與展開層數有關，并且受M×N的影響較大。不管在哪種壓縮率下，CNN-AMP-5 的乘法次數都高于 CsiNet 和CsiNetPlus，這主要是受 ?(·) 模塊的影響。和AMP算法相比，LP-AMP-3 和CNN-AMP-5 的復雜度較低，這是因為它們的展開層數遠小于AMP 的總迭代次數 100。另外，CNN-AMP-5 的復雜度比LP-AMP-3 高，原因在于 ?(·) 模塊使用了連續的卷積層。

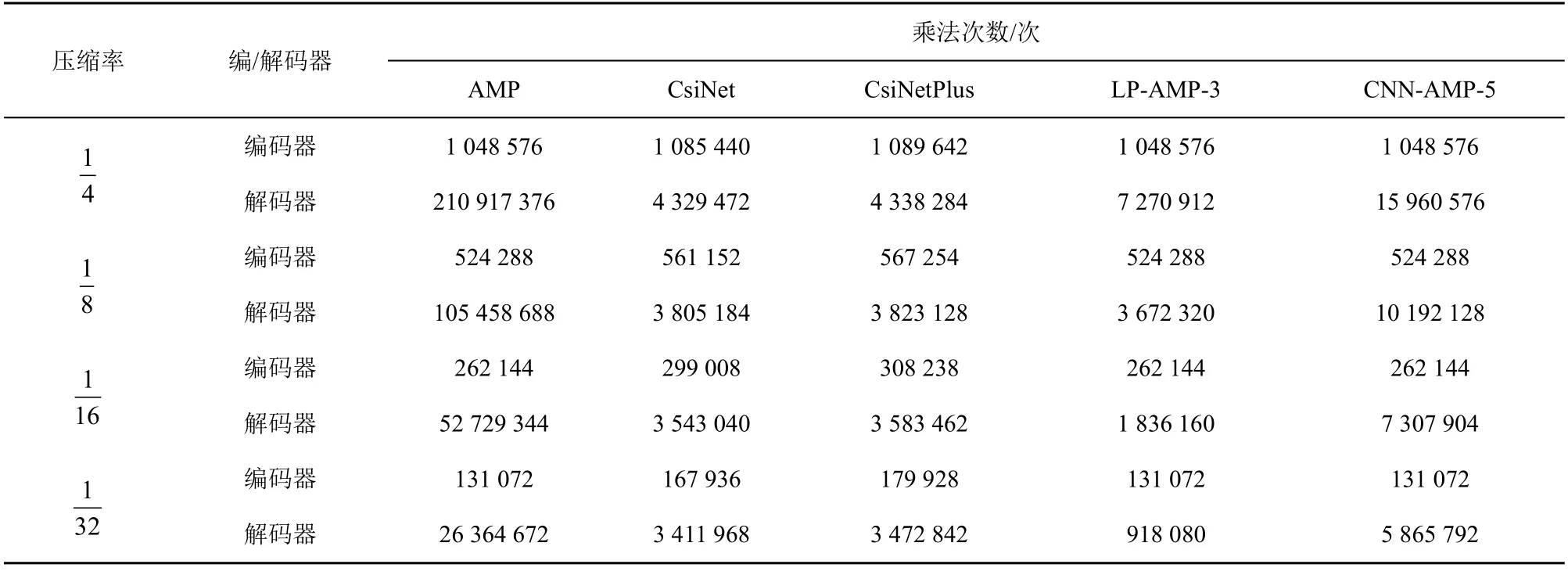
表3 不同算法的乘法次數

4 仿真分析

本節將對比 LP-AMP-3、CNN-AMP-5、CsiNet、CsiNetPlus 和AMP 算法的CSI 反饋性能。經兩次DFT 得到角度時延域矩陣H，保留該矩陣的前=32 行，因此復數矩陣H的維度為32×32，再將復數矩陣改為實虛部雙通道矩陣。壓縮率，M=512、256、128、64，N=2 048。在MATLAB 平臺進行仿真，設備配置與第3 節相同，仿真系統主要參數如表4 所示，其他參數都遵循文獻[21]中的默認設置。

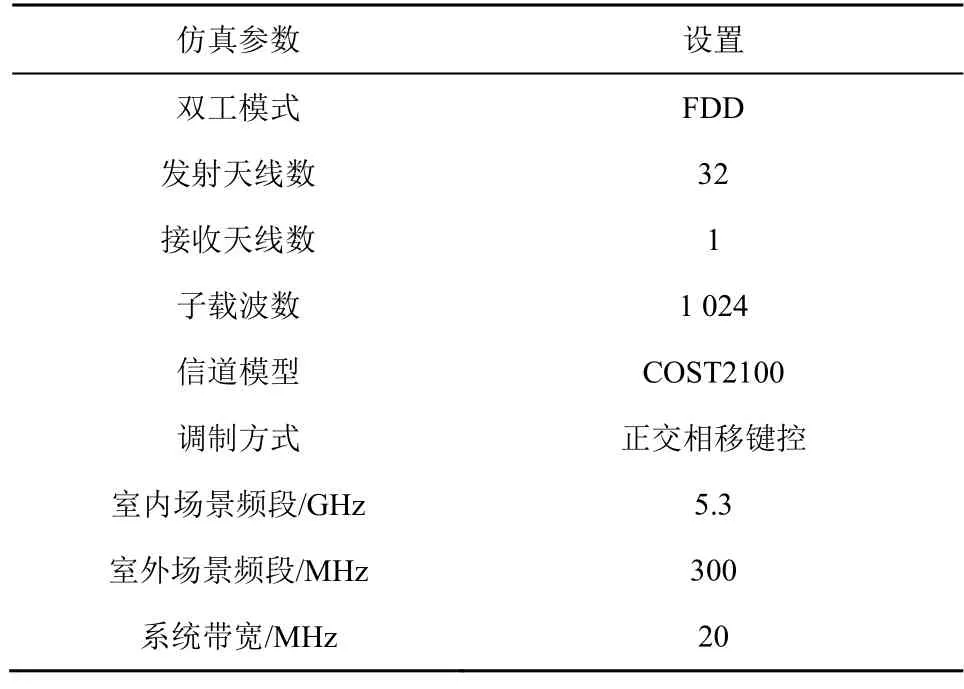
表4 仿真系統主要參數

4.1 歸一化均方誤差

將離線訓練好的模型應用于室內室外場景下的測試集，并通過計算原始矩陣與重構矩陣之間的歸一化均方誤差（NMSE,normalized mean squared error）對模型的性能進行量化評估。NMSE的計算式為

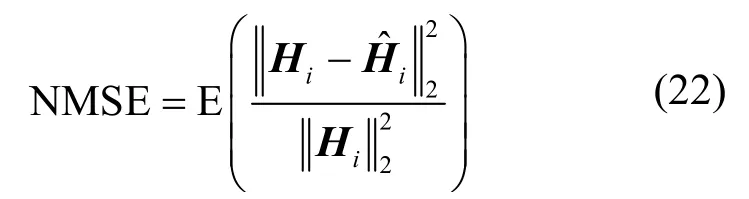
其中，Hi和分別表示原始信道數據和恢復信道數據。不同方法在室內和室外場景下的NMSE如圖9 所示。

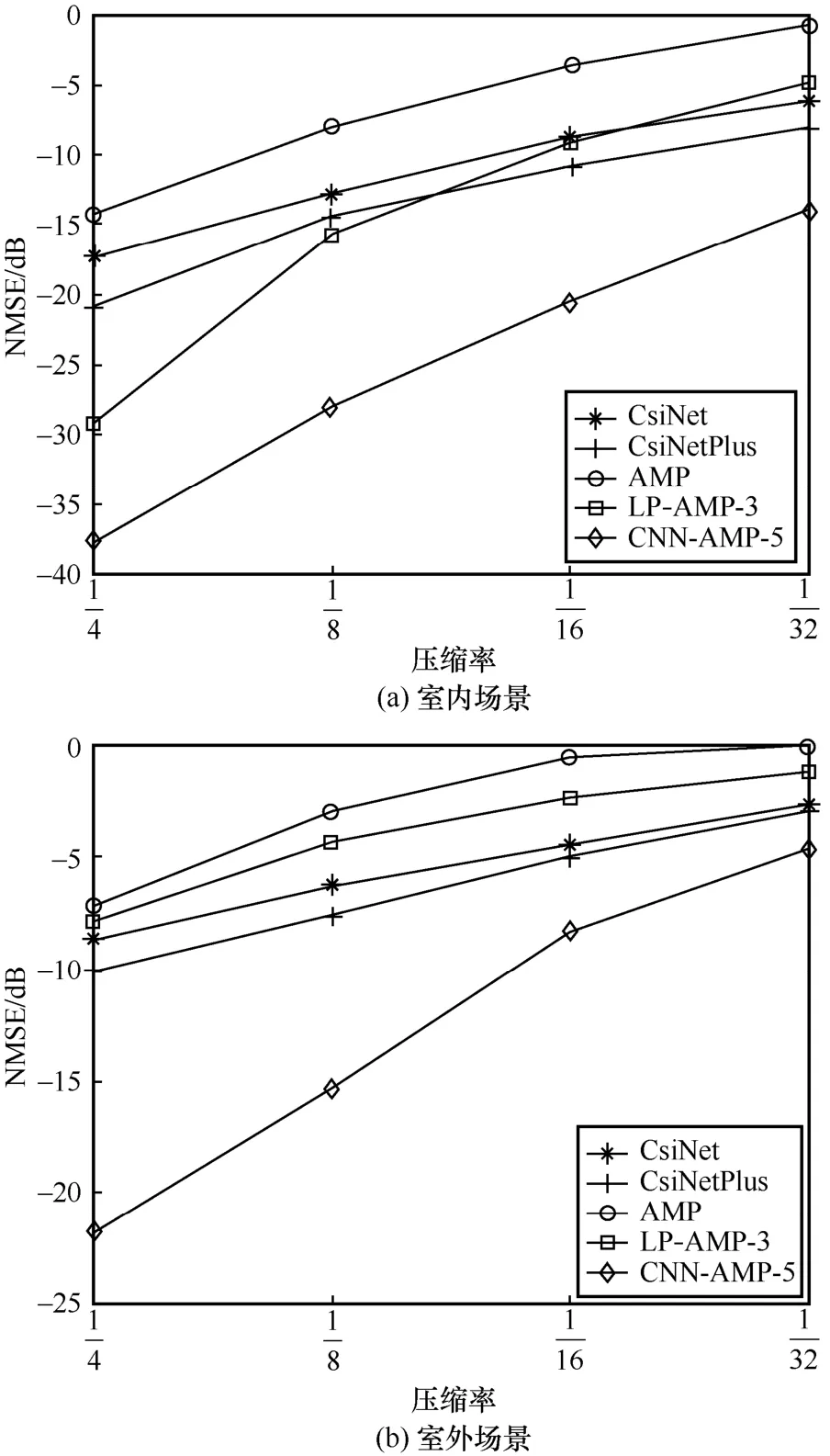
圖9 不同方法在室內和室外場景下的NMSE

4.2 相似度

除NMSE 之外，余弦相似度ρ同樣可以用來對比不同算法之間CSI 矩陣的重構精度。該指標可以體現重構的CSI 矩陣與原始CSI 矩陣之間的相似程度，其計算式為

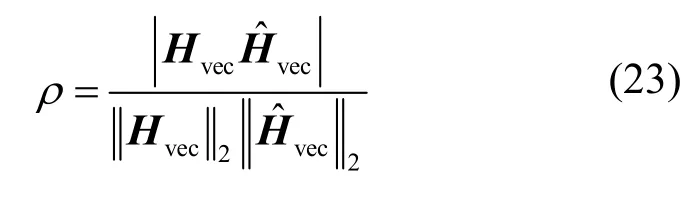
其中，Hvec、分別表示向量化后的CSI 信道矩陣和重構的CSI 信道矩陣，ρ值越大，說明兩者越相似，重構精度越高。不同方法在室內和室外場景下的余弦相似度如圖10 所示。

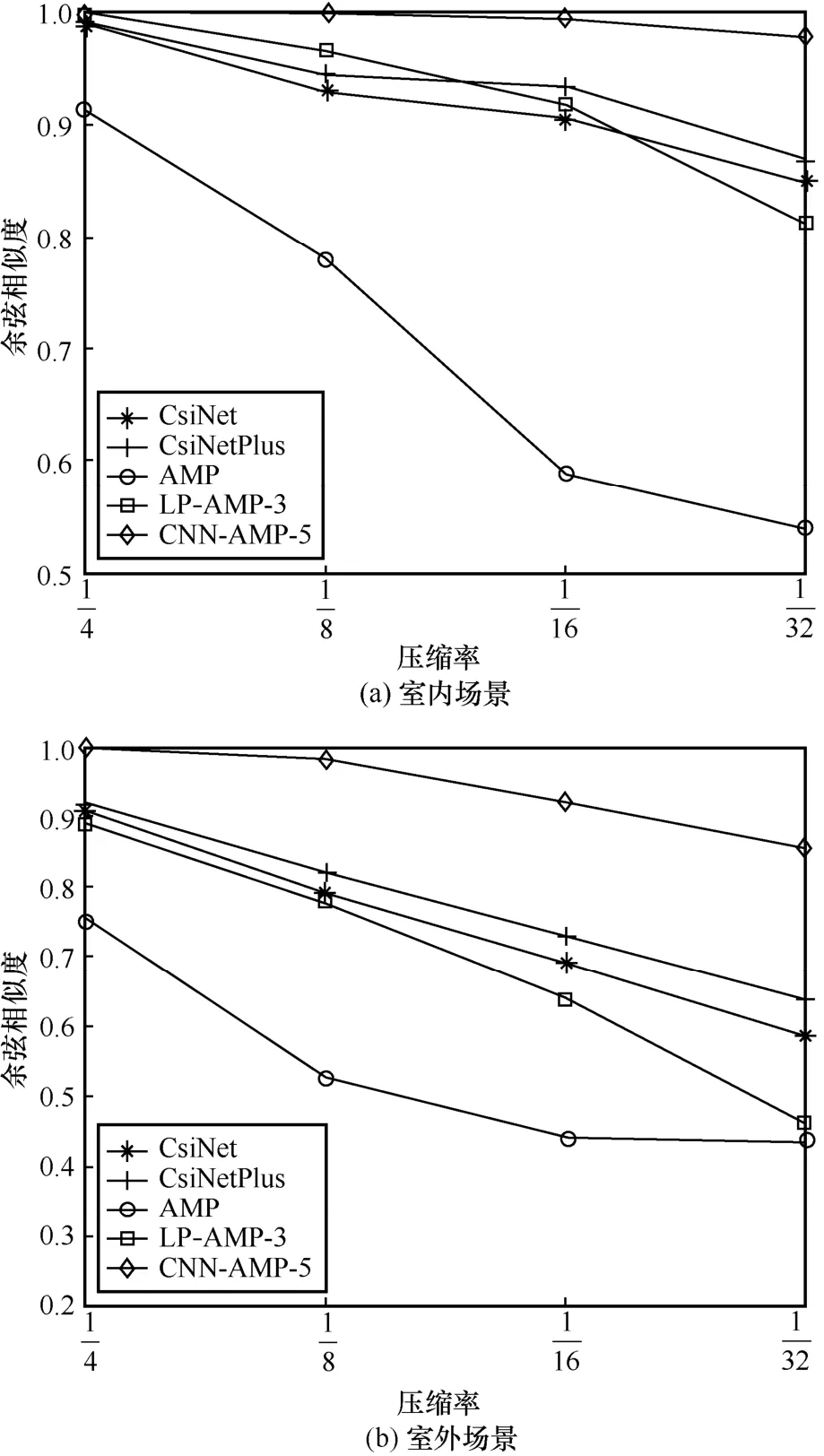
圖10 不同方法在室內和室外場景下的余弦相似度

由圖10 可知，經典壓縮感知的AMP 算法在不同場景、不同壓縮率下的ρ均低于其他幾種算法，即CSI矩陣的重構相似度均低于其他算法。在室內場景下，AMP 算法在壓縮率為時ρ明顯下降，而在室外場景下，AMP 在各壓縮率下的ρ都不夠理想，已無法滿足大規模MIMO 系統CSI 反饋的精度要求。LP-AMP-3 算法在室內場景的不同壓縮率下的ρ與CsiNet 和CsiNetPlus 算法比較接近，在室外場景的不同壓縮率下的ρ略低于CsiNet 和CsiNetPlus 算法。CNN-AMP-5 算法不僅在室內場景的不同壓縮率下保持較高的ρ，在室外場景下也有著優異的表現，可以滿足大規模MIMO 系統CSI 反饋的精度要求。

5 結束語

本文研究了基于深度展開的大規模 MIMO CSI 反饋算法。在AMP 算法迭代過程的基礎上，從2 個角度將其深度展開，提出了基于可學習參數的AMP 深度展開算法LP-AMP 和基于卷積殘差學習模塊的AMP 深度展開算法CNN-AMP。針對信道矩陣的非嚴格稀疏性的問題，LP-AMP 通過深度學習的方法改進了閾值函數，增強了AMP 算法應對室內場景的性能，降低了算法的復雜度。在室外場景下，隨著信道矩陣的劇烈變化，非嚴格稀疏性問題逐漸增大，針對這個問題，本文又提出CNN-AMP 算法，將LP-AMP 算法中改進的閾值函數模塊替換為卷積殘差學習模塊，該模塊可以消除AMP 算法在每次迭代更新后重構向量中的高斯隨機噪聲。因此無論是在室內場景下還是在室外場景下，與代表性算法相比，所提算法都有明顯的優勢。本文提出的基于深度展開的CSI 反饋算法既具有壓縮感知算法的可解釋性理論保障，又具有深度學習方法的高性能表現，可以為大規模MIMO CSI反饋提供一些參考，未來還可以從降低復雜度方面對算法進行改進。