破思維定勢 變思維角度 提思維品質
——例談解析幾何中與“聯立”相關的思維定勢
金一鳴 常梨君
(江蘇省常州市田家炳高級中學 213001)
1 問題提出
思維定勢(thinking set),也稱“慣性思維”,是由先前的活動而造成的一種對活動的特殊的 心理準備狀態,或活動的傾向性.在數學問題 解決中,思維定勢對問題解決有積極的一面:利用已有知識、經驗與當前問題情境建立聯系,進行比較,把新問題化歸成一個已解決的熟知舊問題. 思維定勢亦有消極的一面:易產生思想上的惰性, 養成呆板的解題習慣.尤其當新舊問題形似質 異時,思維的定勢會使解題者步入誤區,造成知識和經驗的負遷移,成為束縛創造性思維的一道枷鎖.
面對解析幾何問題,學生畏想、畏算,加之部分教師以考試得分為目的的引導,解答往往只有“三板斧”:一寫標準方程,二列二元二次方程組,三用韋達定理.不可否認這種所謂“直線聯立法”是解決直線與圓錐曲線相交的“通法”,但低級的思維定勢必定阻礙了學生關鍵能力的培養與核心素養的提升,與新課程理念背道而馳.
2 常見思維定勢及思維突破
新高考“反套路,反刷題”,關注數學本質,強調理性思維的價值,注重數學的基礎性,突出關鍵能力的考查,引導學生對數學概念、方法有更深刻的認知.解析幾何問題具有綜合性強、運算量大、題目靈活多變等特點,是考查學生數學運算、數學建模和邏輯推理等核心素養的重要載體.筆者列舉解析幾何中與“聯立”相關的常見思維定勢,探討如何破除思維定勢,變化思維角度,提高思維品質,提升核心素養.
2.1 定勢一:一定利用“直聯法”
例1(2013年全國II卷文)設拋物線C:y2=4x的焦點為F,直線l過點F且與拋物線C交于A,B兩點,若AF=3BF,則l的方程為( ).
A.y=x-1或y=-x+1
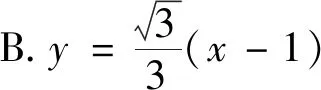
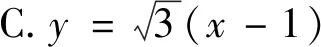
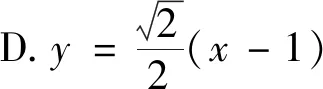

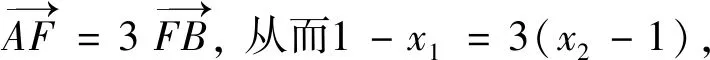
點評利用直聯法(直線與拋物線聯立+韋達定理)設而不求構造關于k的方程,是解決本題的常規思路.事實上,利用算兩次思想,將AF=3BF進行雙重解讀,直接構造點坐標的二元方程,可以得到A,B是定點,進而求出斜率,此法更直接明了.
2.2 定勢二:一定選擇直線聯立
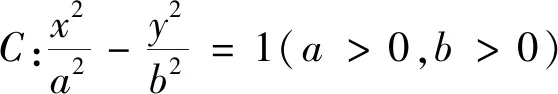
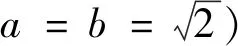
(2)點A,B,D是雙曲線C上不同的三點,且B,D兩點關于y軸對稱,△ABD的外接圓經過原點O,求證:直線AB與圓x2+y2=1相切.
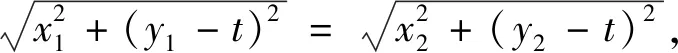
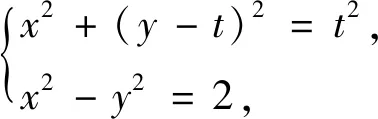
點評本題的關鍵之處在于如何利用y1y2=1得到雙參數m,n之間的關系.以A,B兩點為研究對象,利用其為三種曲線(直線、圓、雙曲線)公共點的身份,將思維從直線與曲線聯立中解脫出來,引入曲線與曲線聯立,“算兩次”得到m,n的關系式,從而簡便求解.
2.3 定勢三:一定利用直線消元
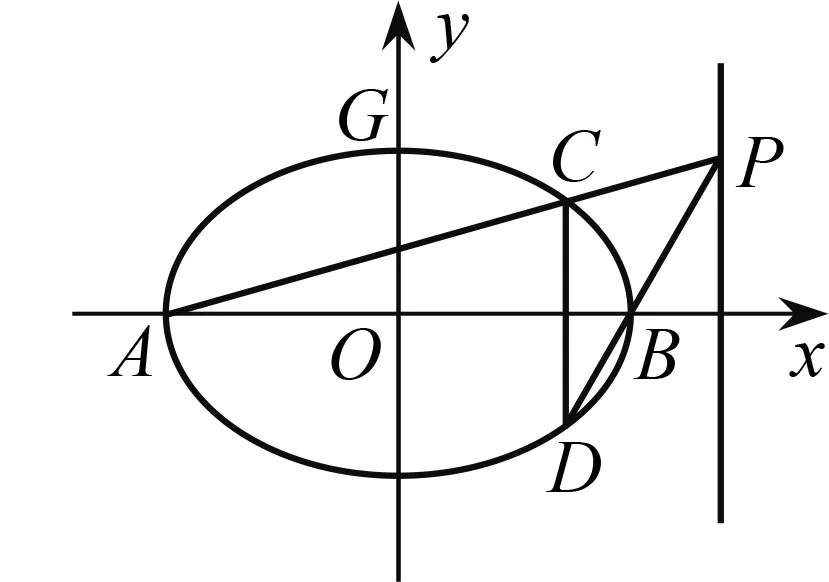
圖1
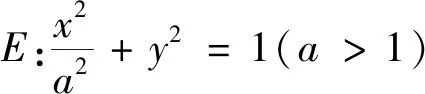
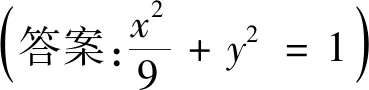
(2)證明:直線CD過定點.
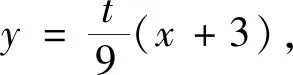
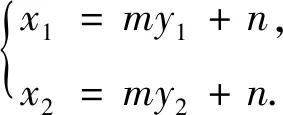
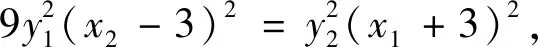
點評本題的關鍵是四元表達式3y1(x2-3)=y2(x1-3)的化簡,利用直線x=my+n消元化為2my1y2+3(n-3)y1-(n+3)y2=0,但這個表達式“不對稱”,直接利用韋達定理不方便,需要進一步轉化.轉換視角,利用點在橢圓上消元,可直接得到4x1x2-15(x1+x2)+36=0,后續求解自然水到渠成.
2.4 “聯立”的教材溯源
翻閱人教A版選擇性必修一,與聯立相關的內容在解析幾何各個章節中都有滲透,以具體的例題為依托,大多以“位置關系判定”“求弦長”為主.曲線方程“聯立”的幾何解釋為:如果曲線C1:f(x,y)=0與曲線C2:f(x,y)=0有公共點,那么公共點滿足曲線C1,C2的方程,即公共點坐標為方程組的解,方程組解的個數是公共點個數.據此判定直線與曲線的位置關系,解決相關后續問題.由上可知,聯立只是一種手段,為何要聯立?誰和誰聯立?聯立后消哪個變量?這些聯立背后的底層邏輯需要厘清.
3 三點啟示
3.1 形成定勢,夯實解幾之基
將幾何對象坐標化、方程化,再進行代數討論,最后把運算結果“翻譯”成相應的幾何結論,這就是用坐標法解決平面幾何問題的“三部曲”.幾何量的坐標化最終都可以歸結到“點的坐標化”,聯立的目的就是求點的坐標,如果點的坐標可解,那么整個問題就迎刃而解,但坐標求解后常為含參多元,所以常利用“設而不求”的思想.“直線與二次曲線聯立”是解析幾何在“代數討論”中常用的一種通法,其解題模式如圖2,這種解題模式能幫助我們快速解決一部分直線與圓錐曲線相交的問題.
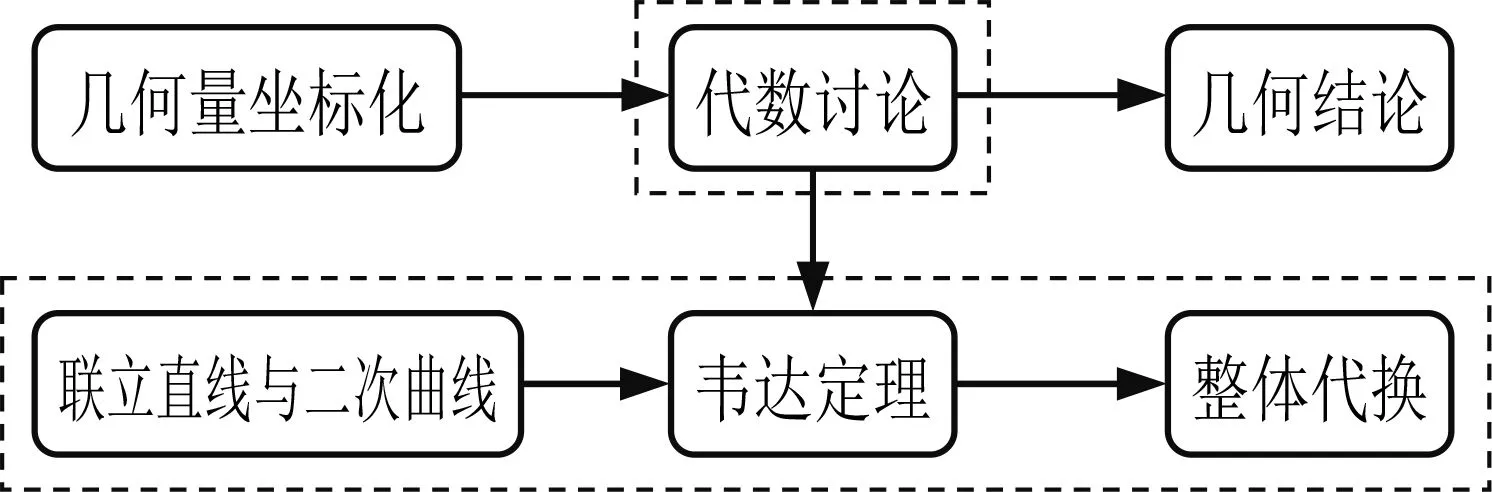
圖2
從行為主義的角度來看,學習是刺激和反應建立聯系的過程,刺激呈現方式、反應后的強化以及重復練習的數量等是影響刺激與反應之間建立聯系的主要因素.因此,對于解析幾何教學,將“直線聯立法”進行一定量的訓練與強化并形成定勢,可以有效縮短學生解決問題的時間,提升解題技能,提振數學學習的信心.
3.2 突破定勢,回歸解幾之源
從“注重圖形分析,巧妙坐標轉化”著手,破除唯“直線聯立法”論,探索解析幾何解題的基本思路才是解析幾何教學的方向.從不同視角將幾何量坐標化,最終的化簡結果殊途同歸,但運算量卻差異很大.以例1中“直線l過點F且與拋物線C交于A,B兩點,若AF=3BF”這個條件坐標化為例(表1),已知F(1,0),設A(x1,y1),B(x2,y2).

表1
由上可以看出,解析幾何的“坐標化”可以從位置關系(點、直線、曲線三者位置關系),距離(點點距、點線距、線線距),角(三角形內角、傾斜角、向量夾角)等方向入手.一方面,在定勢突破過程中,教師要不斷引導學生厘清解題思路與方法,明確相關解題方法的內在原理與底層邏輯;另一方面,教師要鍛煉學生根據現有問題選擇恰當解題方法的能力,讓學生從解數學題走向解決數學問題.
3.3 體悟思想,提升核心素養
“形成定勢”,再“突破定勢”,使學生在“先立后破,破后再立”的過程中掌握解決解析幾何問題的基本思路.學生解題的目的不能僅僅停留在獲得答案的淺水區,而應該在數學問題的解決過程中,通過獨立思考、自主學習、合作交流等多種學習方式,激發學習數學的興趣,養成良好的學習習慣,促進實踐能力和創新意識的發展.教師更要通過自身的引導,讓學生領悟問題背后的數學思想,促進學生思維的提升,從而進一步促進學生數學核心素養的形成和發展.

