Hardy空間上的Volterra-復(fù)合算子①
丁宣浩, 邵長(zhǎng)慧, 李永寧
1.重慶工商大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 重慶 400067; 2.經(jīng)濟(jì)社會(huì)應(yīng)用統(tǒng)計(jì)重慶市重點(diǎn)實(shí)驗(yàn)室, 重慶 400067
本文中記D為復(fù)平面上的單位圓盤, ?D為單位圓周. 單位圓盤上的Hardy空間[1]H2定義為: 由單位圓盤上的解析函數(shù)所構(gòu)成的Hilbert空間. 設(shè)L2(?D)為單位圓周上的Lebesgue平方可積函數(shù)全體, Hardy空間的另一常用定義為

Volterra算子是算子理論中一類重要的有界線性算子, 在很多數(shù)學(xué)分支, 例如線性微分方程的初值問(wèn)題、 優(yōu)化、 種群動(dòng)態(tài)等問(wèn)題上有著重要應(yīng)用. Hardy空間H2上的經(jīng)典的Volterra算子定義為
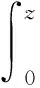
該算子是緊的、 擬冪零的, 沒有特征值且譜集只有零點(diǎn)的線性算子[3]. 文獻(xiàn)[4]給出了Hardy空間上Volterra算子的不變子空間的刻畫:M是V的不變子空間當(dāng)且僅當(dāng)M=znH2(D), 這里n∈N. 這之后, 文獻(xiàn)[5]研究并解決了定義在Hp空間上的Volterra型積分算子
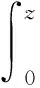
的有界性和緊性的刻畫問(wèn)題, 緊接著, 文獻(xiàn)[6]給出了該算子在Bergman空間上的有界性和緊性的充要條件. 隨后, 文獻(xiàn)[7]給出了該算子在BMOA空間上的有界性和緊性的完全刻畫. 文獻(xiàn)[8]研究了單位圓盤Hardy空間上的復(fù)Volterra算子的不變子空間問(wèn)題.

Cφf(shuō)(z)=f°φ(z)f∈H2
稱為H2上的由φ導(dǎo)出的復(fù)合算子[9]. 復(fù)合算子是解析函數(shù)論與算子理論相結(jié)合的產(chǎn)物, 它是泛函分析中一類十分有趣的具體算子, 其研究推動(dòng)著算子理論的發(fā)展, 并在動(dòng)力系統(tǒng)、 遍歷理論、 解析函數(shù)論等數(shù)學(xué)領(lǐng)域中有著重要的應(yīng)用. Hardy空間上復(fù)合算子的研究涉及算子理論與解析函數(shù)中許多經(jīng)典結(jié)果之間的聯(lián)系, 目前該類算子的研究已經(jīng)取得比較系統(tǒng)的理論成果. 關(guān)于不同函數(shù)空間上的復(fù)合算子的范數(shù)、 有界性、 緊性、 譜、 Schatten類的結(jié)果可參見文獻(xiàn)[9-12].
文獻(xiàn)[11]用Berezin變換的方法研究了廣義Fock空間的Volterra算子與復(fù)合算子乘積的有界性、 緊性、 Schatten-p類性質(zhì)及本性范數(shù)估計(jì). 這激發(fā)了我們引入Volterra-復(fù)合算子Vφ, 其定義為
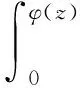
由該算子的定義可知Vφ=CφV, 這是我們將Vφ命名為Volterra-復(fù)合算子的一個(gè)原因.
文獻(xiàn)[13-14]研究了Hardy空間上Volterra算子的其他性質(zhì). 關(guān)于Hardy空間上算子理論的研究, 雖然已經(jīng)有超過(guò)60年的歷史, 但仍煥發(fā)著勃勃生機(jī). 本文的第一、 第三作者和其他人合作分別研究了Hardy空間及其子空間上的一些算子的性質(zhì)[14-16], 這些結(jié)果對(duì)于研究其他函數(shù)空間上的算子理論有著積極作用.
在本文中, 記σ(Vφ)為Volterra-復(fù)合算子Vφ的譜. 設(shè)T是Rn上的線性變換, 則T的核定義為
ker(T)={X∈Rn:T(X)=0}
本文安排如下: 首先, 回顧了Volterra算子和復(fù)合算子的研究結(jié)果, 并引入了Volterra-復(fù)合算子Vφ的定義; 在第一節(jié), 刻畫Vφ的有界性、 緊性、 核等一些基本性質(zhì); 在第二節(jié), 給出Volterra-復(fù)合算子Vφ的特征值和奇異值.
1 基本性質(zhì)
本節(jié)主要討論Volterra-復(fù)合算子Vφ的有界性、 緊性以及核的刻畫, 給出了3個(gè)定理.

下述結(jié)論給出了Volterra-復(fù)合算子的范數(shù)估計(jì):

證因?yàn)閂φ=CφV, 并且對(duì)?f∈H2,f有冪級(jí)數(shù)展開式
將f(z)代入Vf(z), 則有
特別地, 因?yàn)?/p>
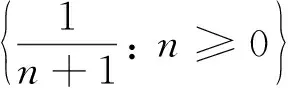
這樣便有了
‖Vφ‖=‖CφV‖≤‖Cφ‖‖V‖=‖Cφ‖
又由引理1可知
從而可以得到



證設(shè)f∈H2, 使得
Vφf(shuō)=0
即
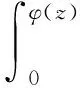
兩邊同時(shí)對(duì)z求導(dǎo), 則可得f(φ(z))φ′(z)=0. 由于φ是非常值函數(shù), 所以φ′(z)≠0, 從而f(φ(z))=0, 即f|φ(D)=0. 又因?yàn)棣?D)?D且f為解析函數(shù), 由解析函數(shù)的零點(diǎn)定理知, 對(duì)z∈D, 恒有f(z)=0, 從而kerVφ={0}.
2 特征值與奇異值
本節(jié)主要討論了Volterra-復(fù)合算子Vφ的特征值和奇異值問(wèn)題.

定義1設(shè)H是可分的Hilbert空間,T是H上的有界線性算子, 若對(duì)λ∈C, 存在非零向量x∈H, 使得Tx=λx, 則稱λ是T的特征值, 稱x是T的對(duì)應(yīng)特征值λ的特征向量.

證假設(shè)λ≠0是Vφa的特征值, 則存在非零函數(shù)f∈H2, 使得Vφaf=λf, 即
CφaVf=λf
首先等式兩邊作用復(fù)合算子Cφa, 可得
CφaCφaVf=λCφaf
注意到
CφaCφa=I
從而
Vf(z)=λf°φa(z)
(1)
再將V作用于等式(1)的兩邊, 由φa°φa(z)=z可得
V2f(z)=λVf°φa(z)=λ(λf°φa°φa(z))=λ2f(z)
(2)

代入(2)式, 得
(3)
比較(3)式中左右兩端z的系數(shù), 則

同理比較(3)式兩端z2的系數(shù), 可得



下述定理給出了Vφ的奇異值刻畫:

證由φ為內(nèi)函數(shù)且φ(0)=0, 根據(jù)引理2可知Cφ為等距算子, 即有
這樣我們可以得到
又因?yàn)?/p>
所以
從而可以得到V*1=0.
同理, 由于
所以有
從而
于是

例1設(shè)φ=zN, 其中N為大于1的正整數(shù), 則σ(Vφ)={0}.
證假設(shè)λ≠0是Vφ的特征值, 那么存在非零函數(shù)f∈H2, 使得
Vφf(shuō)=λf
根據(jù)定義知
則有
(4)
首先, 比較(4)式兩端的常數(shù)項(xiàng), 可得





