一類帶記憶項半線性時間分數(shù)階σ-發(fā)展方程解的爆破①

何鑫海， 陳雪麗， 楊晗

西南交通大學(xué) 數(shù)學(xué)學(xué)院， 成都 611756

本文研究以下半線性時間分數(shù)階σ-發(fā)展方程的柯西問題：

(1)

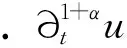
(2)

這里

為Riemann-Liouville型積分， Γ(β)為Gamma函數(shù)． 算子(-Δ)σ定義為

上述時間分數(shù)階σ-發(fā)展方程(1)在物理學(xué)、 力學(xué)和其他應(yīng)用科學(xué)中有著大量應(yīng)用[1-3]， 通常用于刻畫具有冪律變特性的粘彈性介質(zhì)中機械波的傳播問題， 也可描述介于擴散和波傳播模型的中間現(xiàn)象， 且這種現(xiàn)象通常發(fā)生在粘彈性介質(zhì)中， 融合了表現(xiàn)波傳播的類固體材料和支持擴散過程類流體材料的特性， 近年來關(guān)于該類方程解的適定性研究引起了不少研究者的關(guān)注[4-7].

注意到非線性項有如下性質(zhì)

進而有

因此， 當(dāng)指數(shù)γ→1-且參數(shù)α，σ取極限情形時， 本文所研究的非線性記憶項的柯西問題(1)可轉(zhuǎn)化為非線性項為|u|p的經(jīng)典問題． 探討問題(1)與經(jīng)典柯西問題解的性質(zhì)之間的聯(lián)系是一件很有意義的事情.

當(dāng)α=0，σ=1，γ=1時， 問題(1)轉(zhuǎn)化為如下半線性熱傳導(dǎo)方程的柯西問題：

當(dāng)α=0，σ=1，γ∈(0， 1)時， 問題(1)則轉(zhuǎn)化為如下帶記憶項半線性熱傳導(dǎo)方程的柯西問題：

文獻[11]證明了在

時解在有限時刻爆破， 并證明了p>p?時小初值情況下存在整體解， 此處

(n-2+2γ)+=max{0，n-2+2γ}

可以看到當(dāng)γ→1-時， 此時的臨界指數(shù)與Fujita臨界指數(shù)一致.

當(dāng)α=1，σ=1，γ=1時， 問題(1)轉(zhuǎn)化為如下半線性波動方程的雙初值問題：

(3)

文獻[12]在

和p>1，n=1時證明了解在有限時刻爆破． 根據(jù)Strauss猜想[13]， 問題(3)的臨界指數(shù)p0(n)為二次方程

(n-1)p2-(n+1)p-2=0

的正根， 并且在n≥2，p>p0(n)時， 問題(3)在小初值情況下存在整體解， 在p≤p0(n)時問題(3)的解在有限時刻爆破． 文獻[14-16]在超臨界情況下針對不同空間維數(shù)證明了整體解的存在性， 文獻[17-18]在臨界情況下、 文獻[19-20]在次臨界情況下分別針對不同空間維數(shù)證明了解的有限時刻爆破.

對于時間分數(shù)階方程， 當(dāng)α∈(0， 1)，σ=1，γ=1時， 問題(1)轉(zhuǎn)化為如下時間分數(shù)階擴散-波動方程的柯西問題：

文獻[4]得到了在小初值情況下，u1=0及u1≠0時該問題的兩個臨界指數(shù)， 分別為

文獻[6]證明了當(dāng)小初值u0∈L1(Rn)∩L∞(Rn)且指數(shù)滿足

時問題(1)存在唯一整體解． 那么在1

定理1當(dāng)α∈(0， 1)，σ≥1，γ∈(0， 1)時， 假設(shè)初值u0∈L1(Rn)∩L2(Rn)且滿足

(4)

若

(5)

T≤Cε-k

其中

C是與ε無關(guān)的正常數(shù).

定義1[21](Riemann-Liouville型分數(shù)階積分) 令T>0，f∈L1(0，T)，α∈(0， 1)階左側(cè)與右側(cè)Riemann-Liouville型分數(shù)階積分分別定義為

與

此處Γ(α)為伽馬函數(shù).

定義2[21](Riemann-Liouville型分數(shù)階導(dǎo)數(shù)) 令T>0，f∈AC[0，T]，α∈(0， 1)階左側(cè)與右側(cè)Riemann-Liouville型分數(shù)階導(dǎo)數(shù)分別定義為

與

對于以上微積分定義， 有如下性質(zhì)成立：

(6)

其中

與

此處要求

命題2[22]令T>0，α∈(0， 1)， 則對任意f∈Lr(0，T)， 1≤r≤∞， 等式

在t∈(0，T)上幾乎處處成立.

此處f∧g表示存在一正常數(shù)C， 滿足f≤Cg.

引理2[23]令σ≥1， 記φ=φ(x)=〈x〉-q，q>0． 對于任意R>0， 定義φR為

φR(x)=φ(x/R)x∈Rn

則(-Δ)σ(φR)滿足以下伸縮變換性質(zhì)

(-Δ)σ(φR)(x)=R-2σ((-Δ)σφ)(x/R)x∈Rn

在證明爆破之前， 通過Caputo型分數(shù)階導(dǎo)數(shù)的定義(2)及分部積分公式(6)， 先給出問題(1)弱解的定義.

定義3令p>1，T>0，u0∈L2(Rn)． 若函數(shù)

u∈Lp([0，T]，L2p(Rn))∩L1([0，T]，L2(Rn))

且對任意測試函數(shù)φR(x)∈H2σ(Rn)，φ(t)∈C2([0，T])， 有

(7)

則稱u是問題(1)的局部弱解． 若T=∞， 則稱u是問題(1)的整體弱解.

關(guān)于此測試函數(shù)， 有

且有如下求導(dǎo)性質(zhì)：

引理3[22]令T>0，α∈(0， 1)，β>α， 對任意t∈[0，T]， 存在C=C(α，β)， 有

以及

定理1的證明

引入測試函數(shù)

φR(x)=φ(x/R)φ(x)=〈x〉-n-2sσ∈C∞(Rn)

在Rn上可積． 這里

[σ]為σ的取整． 由引理1， 可以看出對?σ≥1， 有

|(-Δ)σ〈x〉-n-2sσ|∧〈x〉-n-2sσ

現(xiàn)將測試函數(shù)φR和φ帶入(7)式中， 有

以及

從而有

(8)

(9)

由(5)式， 當(dāng)且當(dāng)p

令T→∞， 可以推出

故u=0， 這與假設(shè)(4)矛盾， 所以問題(1)在次臨界條件下不存在整體解.

當(dāng)p=pc時， 有

此時令

由(8)式及Young不等式可得

當(dāng)K足夠大時， 由(5)式可以推出

同樣產(chǎn)生了矛盾， 故問題(1)在臨界條件下不存在整體解.

由(9)式可知

T≤Cε-k

其中

C是與ε無關(guān)的正常數(shù).