運用代理模型的超低溫閥優化設計*

方宇豪，王守真，王 帥，王林濤

(1.大連理工大學機械工程學院，遼寧 大連 116024；2.大連船用閥門有限公司，遼寧 大連 116024)

0 引言

近些年，我國的航天等產業發展迅速，伴隨著這些產業的發展，對于各種特殊介質的儲存、運輸等也有著越來越高的要求，LNG作為其中一種重要的能源，也需要相應的流體控制設備，超低溫閥在其中扮演著相當重要的角色，而對于超低溫閥的設計制造等也提出了越來越高的要求[1]。

超低溫閥(如圖1)是由閥體、閥盤、閥盤壓套、閥蓋、閥桿、填料墊、填料、填料壓套、支架和管道組成。由于超低溫閥的工作環境較為惡劣，流通介質特殊等特點，會產生密封不嚴、流阻過大等問題，故而對超低溫閥門的設計制造等提出了較高的要求。因此，有必要在滿足強度、密封性條件下對超低溫閥進行結構優化設計。

我國對超低溫閥的研究開始于20世紀90年代，鹿彪等探討了超低溫閥門的一些結構，分析了超低溫閥門的材料和實驗[2]。丁強偉對LNG用超低溫截止閥做了熱固耦合分析，分析了超低溫閥門的應力場[3]。楊剛等研究了超低溫球閥的主密封副性能，提出了改善主密封副性能的方法[4]。王宇峰針對閘閥的工作條件進行分析，針對分析結果對閘閥的密封性能提出了一定的改進意見[5]。在這些研究中，不乏針對超低溫閥門進行結構優化的，但是使用的方法較為簡單。

圖1 超低溫閥

以往的優化設計往往是通過有限元方法進行的，但是有限元方法耗費的時間一般比較長，為了解決這個問題，現在的研究中會使用代理模型方法來代替有限元模型來提高計算效率[6]。其中，Kriging模型在解決高維非線性問題時性能較好，使得Kriging模型在工程問題中的應用越來越廣泛[7]。本文通過構建高精度的代理模型，來探究對閥門結構的減阻優化。

1 參數化建模與有限元分析

1.1 參數化建模

通過SolidWorks分別建立閥門各個零件的參數化模型，如圖2所示。選用的為DN50的超低溫截止閥，額定工作壓力2 MPa，進口流速5 m/s，額定工作溫度-162 ℃。為了消除管道長度對流體特性的影響，經過測試，在開啟工況時采用入口處管道長度為4倍通徑，出口處管道長度為8倍通徑。在不改變裝配尺寸的前提下共對該裝配體設置102個參數。其中，有76組參數之間互相關聯，最終作為獨立變量的參數共有26個，將這些作為獨立變量的參數標注在對應的模型上，進行參數化建模，如圖2所示。各個設計變量的參數以及范圍見表1。

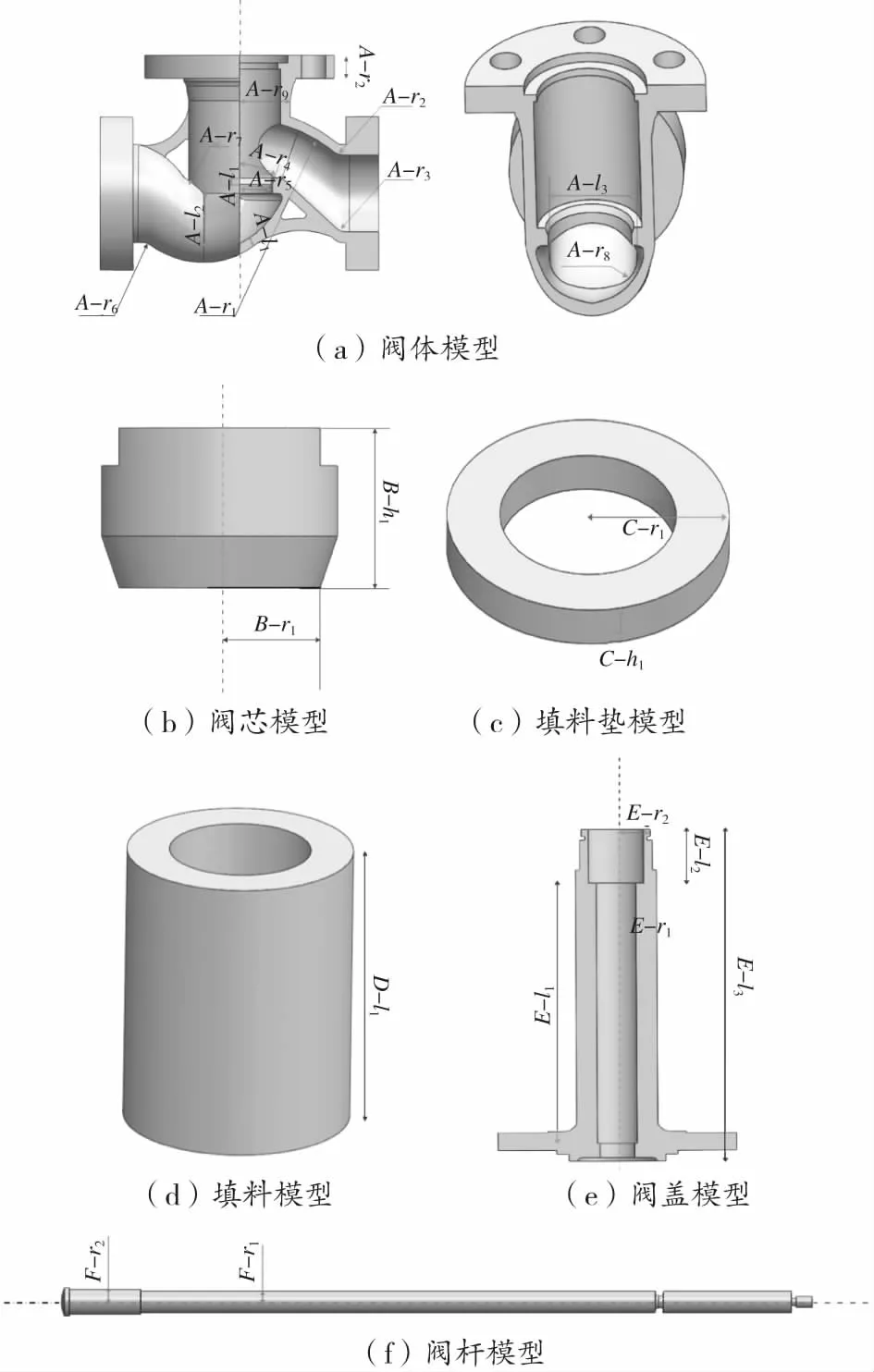
圖2 閥門零件參數化模型

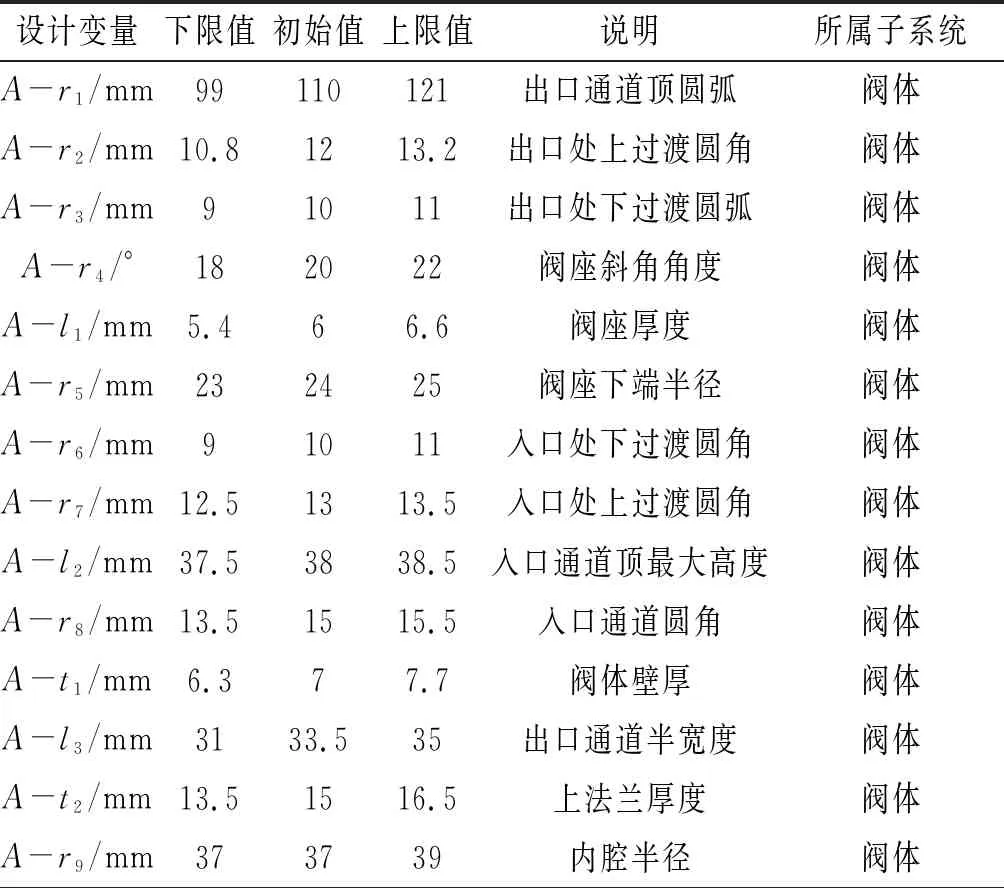
表1 設計變量

續表1

1.2 有限元仿真

1.2.1 載荷分析

超低溫閥門在開啟和關閉的瞬間受到的載荷影響最大，因此要對關閉瞬間的閥門工況進行分析。超低溫閥門關閉時受到的載荷主要有以下三個方面：閥門零件間相互的結構應力、介質壓力、溫度場產生的熱應力。

Ⅰ.填料與閥桿間的摩擦力

QF=πdFhZ1.2PfsinαL

(1)

其中，h是單圈填料的高度，Z為填料的圈數，f為填料與閥桿間的摩擦系數(約為0.05)，αL為閥桿螺紋的螺旋角，填料與閥桿間的摩擦力為381.2 N。

Ⅱ.介質作用力

介質從閥盤下方流入時，閥門密封面總共受到了介質靜壓力和介質密封力：

QMZ=QMJ+QMF

(2)

其中，QMJ為密封面上的介質靜壓力。

(3)

其中，DMN為密封面內徑，bM為閥座密封面寬度，P為計算壓力。計算得QMJ為4085.6 N。

而QMF是介質密封力，對于錐面密封而言

(4)

其中，DMW為密封面外徑，α為錐面半角，fM為密封面摩擦系數(取0.2)，qMF為密封比壓。

(5)

查表得約為6 MPa。計算得QMF為2385.3 N。因此總介質作用力為：

QMZ=4085.6 N+2085.3 N=6470.9 N

(6)

Ⅲ.熱應力

根據設計規范，工作溫度下密封面上產生的平均熱應力為10 MPa，定義熱應力的作用方向總是與閥門密封力方向相反。即：

(7)

考慮極限情況下填料與閥桿摩擦力、介質作用力、熱應力均與密封方向相反，因此預緊力計算公式：

F=QF+QMZ+QT=9993.7 N

(8)

為留有一定余裕且方便計算，將其取為10000 N。

1.2.2 有限元仿真

建立好的參數化模型導入到ANSYS Workbench分別進行熱固耦合分析與流體分析，閥門材料主要采用奧氏體不銹鋼，流體部分采用液氮，材料信息見表2。

表2 材料屬性

對于熱固耦合分析而言，首先生成網格，總體采用5 mm四面體網格，密封面處精度要求較高，采用1 mm網格細化處理，并且采用邊界層，共生成單元數557764，節點數883141。閥盤與閥體的密封面設為摩擦接觸，摩擦系數0.2。將閥桿與閥蓋、閥桿與填料間設為不分離。閥體部分設為-162 ℃，上閥蓋部與空氣接觸，室溫29 ℃，對流換熱系數為15 W/(m2·℃)。閥體上法蘭與進出口采用位移約束，閥體內部工作壓力為2 MPa。對于流體分析而言，首先生成網格，總體采用10 mm四面體網格，在結構變化不平緩處采用1 mm網格細化處理，并且采用邊界層，共生成單元數315210，節點數108150。流體部分采用速度入口5 m/s，壓力出口2 MPa。設置見圖3。

圖3 參數設置

2 仿真結果分析

2.1 應力仿真結果

閥門應力仿真的結果見圖4，收到了溫度場和介質作用力的共同影響，閥門的熱應力主要在閥體內腔，其中在接近上法蘭位置達到最大值，而在其他結構處的應力較小。從圖4可以看出，在閥體內腔處的應力值大約在50 MPa到70 MPa之間，而低溫閥門所用的材料CF3M的屈服強度是243 MPa，遠遠小于材料的屈服強度。同時，閥門的最大應力出現在靠近上法蘭的流道處，達到了105 MPa，此處不止有在約束邊界處的應力奇異，還包括結構的不連續而產生的局部應力集中，屬于正常現象，在可接受的范圍內。為了避免密封結構失效，應保證密封比壓在一定的范圍內，最大密封比壓為23.5 MPa小于許用密封比壓40 MPa。但是平均密封比壓為3.08 MPa，低于達到密封效果的最低密封比壓，因此可能會發生密封失效。

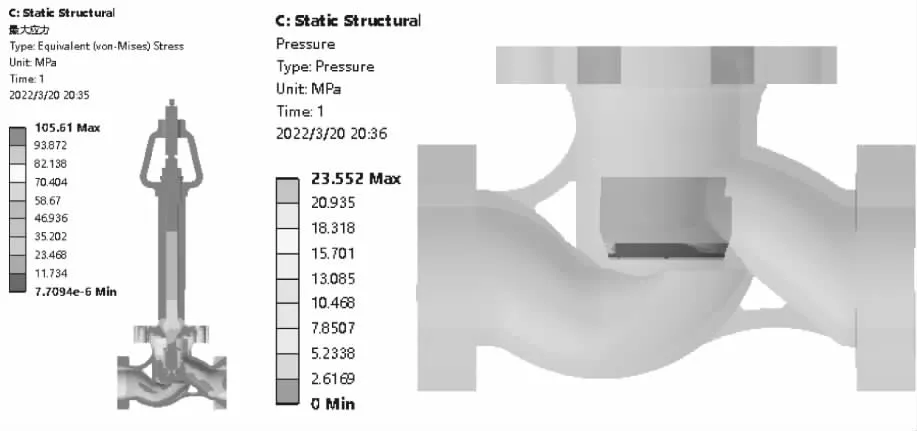
圖4 應力仿真結果

2.2 流體仿真結果

閥門流體仿真的結果如圖5。閥門的流阻系數主要取決于進出口的壓力降與流體的平均流速，而在該超低溫截止閥的工作狀態下，閥門內腔的一些流通截面變化較大處與壁面的影響會對平均流速的影響較大。此次結果平均流速達到了5.19 m/s，且在一些細小截面處最大流速達到了18.8 m/s。因此對于往后要做的設計中應當充分考慮結構對于介質平均流速的影響。

圖5 流體仿真結果

3 Kriging模型

有限元方法分析雖然結果較為精確，但是耗費的時間過長，不利于一些參數較多的非線性問題，因此，可以利用代理模型方法。通過構建超低溫閥門的Kriging模型來代替有限元仿真去進行優化設計。

首先進行試驗設計來構建設計變量空間(S，ys)，S=[x(1)，x(2)，…，x(n)]代表n行設計變量，ys=[y(x(1))，y(x(2))，…，y(x(n))]T代表n組輸出值，并且S與ys之間是一一對應的關系。而Kriging模型[7-8]可以看作是一種特殊的徑向基模型，因此可以用徑向基函數來表示：

(9)

對于該基函數的權值，可以利用高斯隨機分布來計算，即將其視為一個高斯隨機過程：

Y(x)=β0+Z(x)

(10)

其中，β0表示為Y(x)的均值；Z(x)可以看作方差為σ2，均值是0高斯分布。設計空間中每組變量之間可以用基函數來表示關聯性：

Cov[Z(x)，Z(x′)]=σ2R(x，x′)

(11)

在此，可以通過使y(x)值均方差最小的方法來得到式(9)中的權值ω，即：

(12)

最小，并且Kriging模型應使響應值滿足無偏估計：

(13)

在此基礎上，利用拉格朗日乘數法求得模型的預測值和均方差：

(14)

(15)

其中，F是一個n×1階的單位列向量，

β0=(FTR-1F)-1FTR-1ys，

r=[R(x(1)，x)，…，R(x(n)，x)]T。之后求取極大似然函數，從而得到式(11)所需的θ值：

(16)

為了使構建完成的Kriging模型更加符合原有限元模型，應當保證其有足夠的精度，因此在設計抽樣方案時應使樣本盡量具有代表性[9]。通過最優拉丁超立方抽樣法完成抽樣，分別得到800個訓練樣本和200個測試樣本。選擇相關系數r2作為代理模型精度衡量標準，要求其不小于0.9。最終，構建出閥門最大應力、最大變形量、密封比壓、填料底部最低溫度和流阻系數的Kriging模型，代理模型驗證結果如圖6所示。從圖6可以看到，平均密封比壓模型精度略低，但是相關系數r2仍然在0.9之上，滿足要求。

圖6 代理模型驗證結果

4 優化結果

4.1 建立優化數學表達式

根據設計規范與使用要求建立優化數學表達式。閥門的材料選用奧氏體不銹鋼，屈服強度為243 MPa，要求閥門正常工作時的最大應力不超過屈服強度。根據工作規范，閥門正常工作時，最大變形量應小于1 mm。為保證密封面的密封效果，應使密封比壓保持在許用密封比壓之內，根據工作規范，許用密封比壓的范圍為6 MPa≤[σ]≤40 MPa，填料底部的溫度應該在0 ℃之上。綜上所述，以閥門的流阻系數為優化目標，優化數學表達式為：

findx=[x1，x2，x3，…，x26]T

minK(x)

g1=T-t1≤0

g2=σN-[σ]≤0

s.tg3=D-Dmax≤0

g4=[f1-fmin][f1-fmax]≤0

xD≤x≤XU

(17)

其中，設計變量x的取值范圍應該為[xD，xU]。

4.2 求解

建立完優化數學表達式之后，下一步應該尋找最優解。為了避免局部收斂或者求解精度低，找到全局搜索與局部發掘的平衡點，最終選擇一種由MIGA(多島遺傳算法)與NLPQL(非線性二次規劃)相結合的組合算法[10]。該組合算法是結合了兩種算法的長處，首先通過MIGA確定最優解所在的設計空間，然后通過NLPQL在這個區域內尋優，以此得到全局最優解。

使用組合算法的優化過程如圖7所示。從圖7可以看出，優化目標收斂于4.882，g1收斂于0.54 ℃，g2收斂于101.19 MPa，g3收斂于0.955 mm，g4收斂于6.15 MPa。函數初始值和最優解如表3所示。

圖7 迭代過程

表3 初始值和最優解對比

續表3

可以看到，在MIGA全局搜索之后，相較于初始值最大應力減少了2.73%，填料底部最低溫度減少了22.86%，最大變形量增加了0.21%，密封面平均密封比壓增加了102.9%，閥門流阻系數減少了11.15%。利用NLPQL進行局部尋優之后，相較于初始值最大應力減小了4.17%，填料底部最低溫度減少了61.4%，最大變形量增加了0.21%，密封面平均密封比壓增加了99.68%，閥門流阻系數減少了22.3%，從6.28變為4.88，減小了1.4。

分別將迭代后得到的設計變量與響應值代入到原有限元模型中，對比優化目標值與仿真輸出值之間的差距，并且得到它們之間的相對誤差，從而驗證優化結果是否準確，見表4。從表4可得，相比于仿真結果，最終優化結果的相對誤差分別為1.37%，2.77%，-0.21%，0.33%和0.21%。雖然最大應力的相對誤差略高，但是約束g2還遠遠未到約束邊界，2.77%的誤差不會發生失效。因此，Kriging模型的準確度較好，最終優化結果可信。

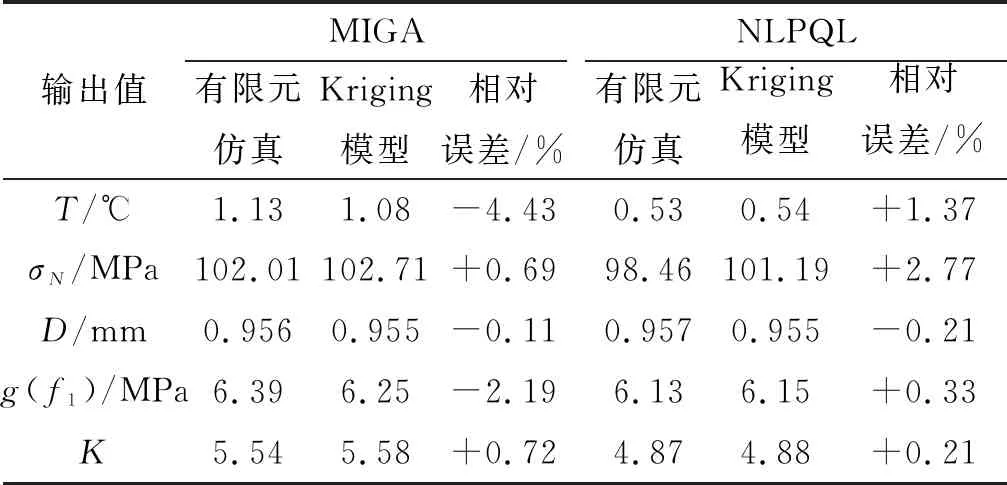
表4 結果對比

5 結束語

通過確定性優化減輕了超低溫閥門的流阻系數，并且確定了其設計變量的設計值，得出了以下結論：

1)超低溫閥門共有26個設計變量，并且經過分析后確定了其可能出現的失效形式。首先對超低溫閥門的各個零件進行參數化建模，最終確定了26個參數作為設計變量開展下一步工作。分別運用有限元進行了熱固耦合仿真與流體仿真，結果表明其密封比壓在工作時易達到下臨界點從而發生失效，因此需要在設計中充分考慮。

2)構建了高精度代理模型。傳統的優化方法對其進行結構優化效率過低，因此構建了Kriging模型作為代替有限元模型來提高優化效率，并且通過拉丁超立方選取實驗點，驗證了代理模型的精度均在0.9以上，符合精度要求。

3)進行優化設計，使超低溫閥的流阻系數降低了22.3%。根據優化目標以及約束條件構建優化方程，通過將MIGA與NLPQL結合的組合算法來進行全局尋優。最終的優化結果表明，流阻系數減小了22.3%，Kriging模型與有限元仿真結果的最大相對誤差為2.77%，說明代理模型的優化結果準確度較高。