新型準零剛度非線性懸置座椅特性分析與參數匹配

趙雷雷 于曰偉 曹建虎 高尚鵬 周長城 袁 建

1.山東理工大學交通與車輛工程學院，淄博，255000 2.北京北汽越野車研究院有限公司，北京，101300

0 引言

農用車輛、工程車輛等工作環境復雜、路況多變，路面及動力總成激勵等引起的振動極易導致車輛及座椅零部件損壞，降低駕乘舒適性[1-3]，損害駕駛員健康[4-6]。目前廣泛應用的剪式座椅作為減小車輛振動關鍵的一環，其懸置隔振性能和使用可靠性顯得尤為重要[7]，然而，生產成本在一定程度上制約了其性能提高。如何提高剪式座椅隔振性能和可靠性并降低其生產成本，已成為當前各車企亟待解決的關鍵問題之一[8-9]。

現有剪式座椅中，傳統座椅采用螺旋彈簧作為懸置彈性元件，成本低、可靠性好，但隔振性能較差[10]，其承載能力與隔振效果之間的矛盾難以調和[11-12]。為有效提高傳統座椅隔振性能，研究人員從電流變[13]、磁流變[14]等可控阻尼的角度進行了有益探索并在一定程度上提高了座椅振動舒適性，但可控減振器成本高且性能可靠性尚待提高[15]，故應用較少。

準零剛度隔振理論為提高傳統座椅性能提供了一條有效路徑，目前在理論上已有很多可行方案[16-17]。閆振華等[18]基于線性螺旋彈簧和球面滾子機構設計了非線性懸置座椅；王勇等[19]研究了基于準零剛度隔振器的車-椅-人耦合系統動態特性；DANH等[20]提出了基于氣動彈簧負剛度的主動座椅系統。在現有諸多方案中，實際工程應用的依然是傳統準零剛度隔振系統，它由一對在垂向產生負剛度的橫置線性彈簧、一個垂向放置的線性彈簧并輔之以定位、導向零部件組成[21-22]。然而，實際工程中該類座椅準零剛度結構零部件易失效，如某個橫置彈簧失效易導致座椅系統運動不穩定、垂向運動摩擦卡滯等，從而使隔振性能惡化，在極大程度上限制了其推廣應用[23-25]。該類座椅推廣應用的關鍵在于保證其隔振性能，優化其隔振拓撲結構并降低復雜性，減少精密零部件種類和數量，建立關鍵參數匹配理論和快速設計方法，這是降低座椅批量制造成本和提高使用可靠性的有效途徑[26]。然而，雖然這種傳統非線性座椅隔振性能好且可有效解決線性座椅弊端，但現有研究依然沒能有效解決其成本高和可靠性差的問題。

針對現有研究的不足，本文在傳統座椅剪式機構基礎上增加連桿和輔助彈簧，提出一種新型非線性懸置座椅系統。

1 新型非線性懸置座椅構型與工作原理

1.1 構型

為解決傳統線性座椅隔振性能差、非線性座椅成本高且可靠性差的問題，在傳統線性座椅剪式機構基礎上增加一個垂置副簧和連桿，提出圖1a所示新型非線性懸置座椅[26]，其中，剪式機構(由剪桿構成)、線性主簧、減振器等均為傳統線性座椅原有組成部分。

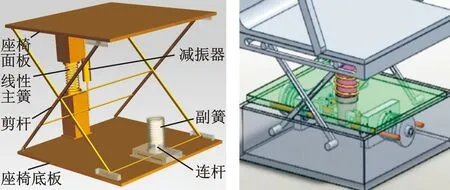
(a)新型非線性懸置座椅 (b)傳統非線性懸置座椅圖1 準零剛度非線性懸置座椅系統示意圖Fig.1 The schematic diagram of the quasi-zero-stiffness nonlinear suspension seat system

圖1b所示為傳統非線性懸置座椅[27]，主要包括剪式機構、一個垂置彈簧和減振器、兩個橫置副簧(輔助彈簧)、兩個連桿及兩套定位零部件。對比可知，新型座椅結構更簡單緊湊，比傳統結構少用一個輔助彈簧、一個連桿及一套定位零部件，僅在傳統線性懸置座椅系統增加副簧和連桿。通過安裝/拆除副簧和連桿，可實現傳統線性懸置座椅和新型非線性座椅轉換，便于工程上實現高低選配。因此，若新型座椅副簧等失效，也能提供傳統剪式線性座椅性能，而傳統非線性懸置座椅中若一個副簧失效，則易導致性能嚴重惡化。可見，新型座椅在結構上決定了其成本僅為傳統非線性懸置座椅系統的一半且可靠性更高。

1.2 工作原理

新型非線性懸置座椅工作原理如下：座椅負剛度機構由常規剪式機構、連桿及副簧組成，它提供座椅垂向運動導向和負剛度隔振雙重功能，主簧提供正剛度，主簧與負剛度機構的共同作用使座椅懸置系統垂向變形與彈性回復力關系曲線的中間呈較長平直段，兩側呈現強非線性特性。在駕乘人員重力作用下，主簧與副簧發生壓縮變形，連桿運動至與座椅底板相垂直位置。車輛受振動激勵時，懸置系統由靜平衡位置開始發生壓縮和復原運動，連桿在垂直位置發生左右擺動，協同減振器的阻尼作用，隔離低頻振動。其中，當懸置系統發生壓縮運動時，主簧的壓縮量增大，副簧的壓縮量減小；當懸置系統發生復原運動時，主簧的壓縮量減小，副簧的壓縮量增大，即在不同工作位置時主簧與副簧始終協同工作。

主簧與副簧的協同作用可實現高靜態剛度和低動態剛度。在靜平衡位置時，新型懸置系統的垂向動剛度接近于零。當座椅在靜平衡位置附近振動時，新型懸置系統動剛度低于傳統線性懸置系統動剛度，可有效衰減座椅垂向振動，此時，新型懸置系統呈現高靜態剛度特性，靜態剛度大于傳統線性懸置系統靜剛度，可實現較好靜態承載。當遠離靜平衡位置時，新型懸置系統具有強動剛度且大于傳統線性懸置系統動剛度，可較好地限制座椅大幅度振動，實現懸置系統限位，有效避免極限工況下座椅懸置撞擊現象。此外，在剪桿與座椅底板之間安裝橡膠防撞塊，也可避免撞擊現象。

2 新型非線性懸置座椅系統建模

2.1 物理模型

圖2所示為圖1a中新型非線性懸置座椅系統的簡化物理模型。設座椅整體坐標系Oxyz原點與座椅初始位置時剪桿與底板上導軌鉸接點S重合，x軸水平向前，z軸垂直向上。設PS=QR=L，AS=a，BR=r，BQ=c。座椅初始位置時，剪桿PS與SR夾角為θ0。在載荷作用下，剪桿PS與SR夾角為θ。座椅初始位置及任意位置各點坐標如表1所示。初始位置幾何尺寸如圖2所示。

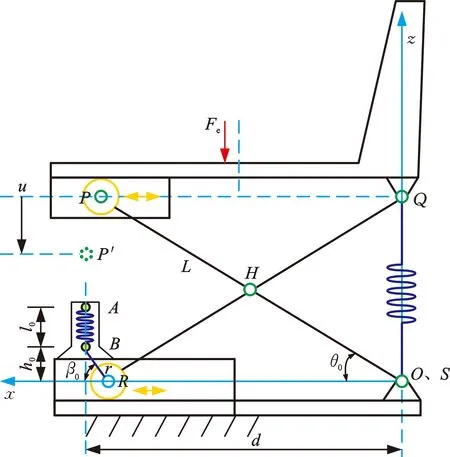
圖2 座椅系統力學模型示意圖Fig.2 The schematic diagram of mechanical model of the seat system

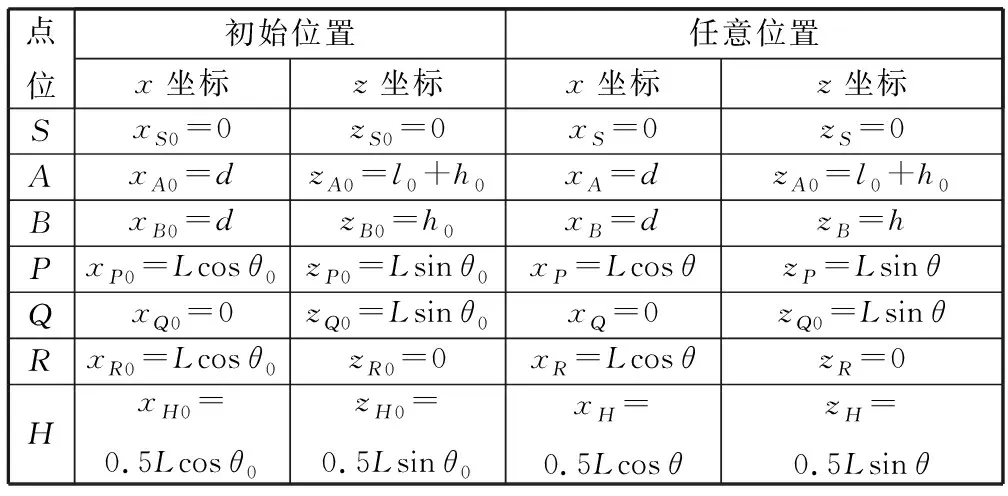
表1 座椅在初始位置及任意位置時各點的坐標Tab.1 The coordinates of each point of the seat at the initial position and at any position

2.2 數學模型

2.2.1力-位移靜力學建模

如圖2所示，座椅初始位置時，設輔助彈簧上下安裝點間距為l0，則高度h0可表示為

(1)

若座椅面板由初始位置產生向下位移u，點P移動到P′點。根據幾何關系可知

zP0-zP=u

(2)

將zP=Lsinθ及zP0=Lsinθ0代入式(2)，可得

Lsinθ0-Lsinθ=u

(3)

由式(3)，可得

sinθ0-u/L=sinθ

(4)

若座椅面板由初始位置產生向下位移量u，則此時B點坐標zB表示為

(5)

此時，R點坐標xR表示為

(6)

將式(6)代入式(5)，可得

zB=

(7)

輔助彈簧由初始位置發生變形后，其安裝點之間距離

l=zA-zB=l0+h0-

(8)

若座椅面板由初始位置產生向下位移u，則輔助彈簧變形量

Δl=l0-l=

(9)

采用螺旋彈簧作為輔助彈簧，則其任意位置彈性壓縮力

Fs=Ks(l0-l)=Ks·

(10)

式中，Ks為輔助彈簧剛度。

在座椅系統中撤去主彈簧，則當輔助彈簧彈性力為Fs時，座椅面板所受外力記為Fn，根據虛功原理，可得

Fnδu-Fsδ(Δl)=0

(11)

根據式(9)～式(11)，虛位移δ(Δl)及負剛度機構垂向力Fn的解析表達式分別為

(12)

Fn=

(13)

在座椅系統中，若主彈簧采用螺旋彈簧且考慮其預變形量u0，則當座椅面板產生位移u時，其彈性力

Fp=Kv(u+u0)

(14)

式中，Kv為主彈簧剛度。

座椅系統中主彈簧和輔助彈簧產生的總垂向彈性力Ft可表示為

Ft=Fp+Fn

(15)

將式(13)及式(14)代入式(15)，可得總垂向彈性力Ft的解析表達式。

2.2.2力-剛度建模

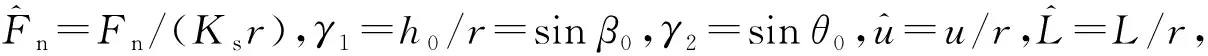
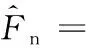
(16)

為滿足座椅隔振及人機工程需求，在座椅剪式負剛度機構設計時，需基于座椅額定載荷匹配合理的座椅懸置垂向變形ue及剪桿與座椅底板夾角θe，故需將式(16)中參數γ1和γ2用ue和θe表示。根據幾何關系，可得

(17)

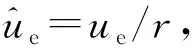
(18)

由式(18)，可得

(19)

將(18)代入式(19)，可得

(20)

2.2.3座椅系統動力學建模

新型座椅系統采用液壓減振器，其阻尼力Fc可表示為[28]

(21)

式中，C0為減振器線性阻尼系數；v1f、v1r分別為減振器復原和壓縮初次開閥速度；v2f、v2r分別為減振器復原和壓縮二次開閥速度；γf、γr分別為復原和壓縮比例系數；vt為減振器相對運動速度。

設座椅在自身和駕駛員總有效質量m作用下，主彈簧產生垂向變形ue后達到靜平衡位置。設座椅垂向位移激勵為q，座椅面垂向位移為z。將Ft中變量u替換為ue-(z-q)并加mg，可得座椅系統以靜平衡位置為零點的整體垂向彈性回復力Fte表達式。根據牛頓第二定律，座椅系統振動微分方程為

(22)

3 新型非線性懸置座椅系統特性分析

3.1 可變承載特性分析

座椅系統承載特性直接影響其隔振性能。駕駛員重量變化可能惡化懸置隔振性能，故需對新型懸置座椅系統的承載特性進行分析。圖1a所示的新型懸置座椅系統參數如下：Kv=20 N/mm，Ks=50 N/mm，θ0=49°，β0=36°，L=600 mm，r=40 mm。在u0依次取值0，5，10，15 mm的情況下，根據式(15)，總垂向彈性力Ft隨相對位移u的變化曲線如圖3所示。

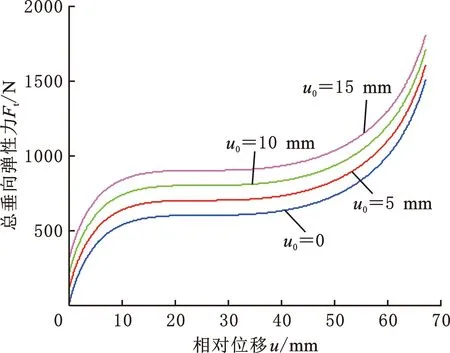
圖3 總垂向彈性力Ft隨相對位移u的變化曲線Fig.3 The curve of the vertical elastic restoring force Ft vs. the displacement u

圖3中曲線中間呈現較長平直段，兩側呈現強非線性特性，其中，平直段對應的Ft值表征座椅系統靜態承載能力。當主簧預變形量u0增大時，Ft值隨之增大，懸置可承載的有效質量依次為60，70，80，90 kg。可見，新型懸置座椅系統可通過主簧3的安裝來調節其預變形量u0，以適應不同體重的駕駛員。

3.2 負剛度機構靜力學特性分析

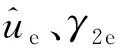
表2 量綱一變量的取值范圍Tab.2 The value range of the dimensionless variables

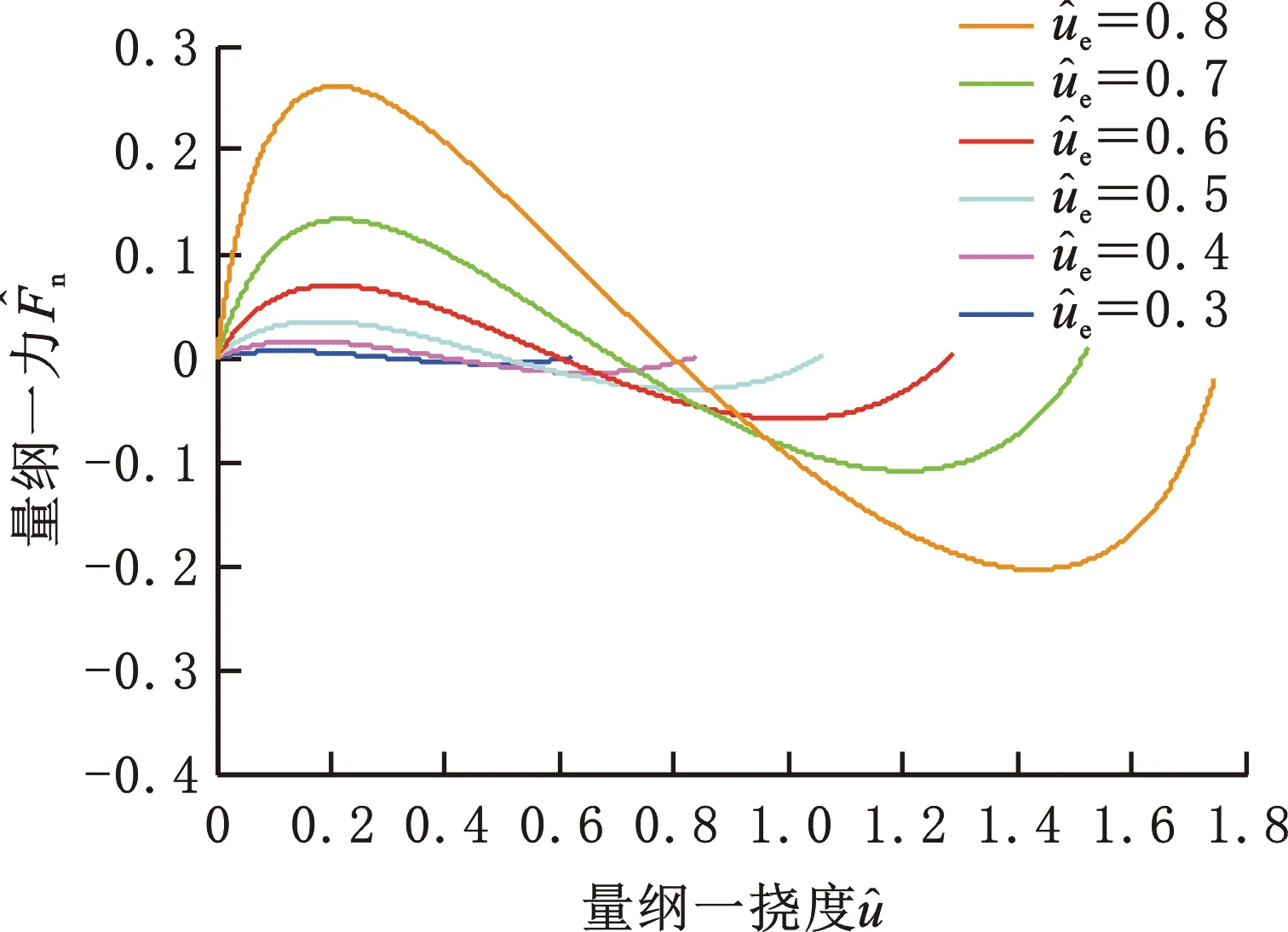
對的影響

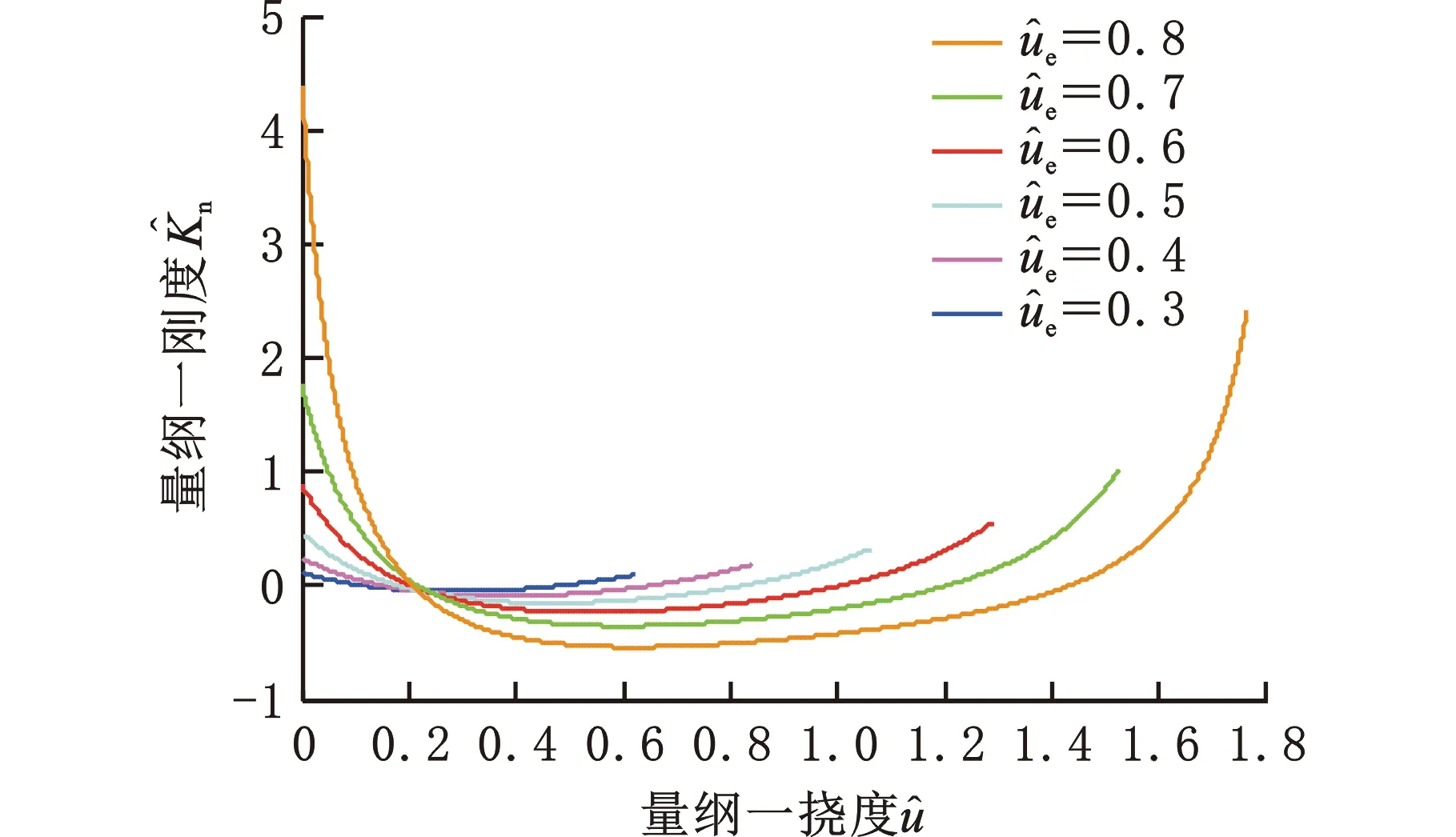
對的影響圖4 不同取值時和隨變化曲線Fig.4 The curves of and vs. different values of

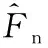
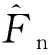
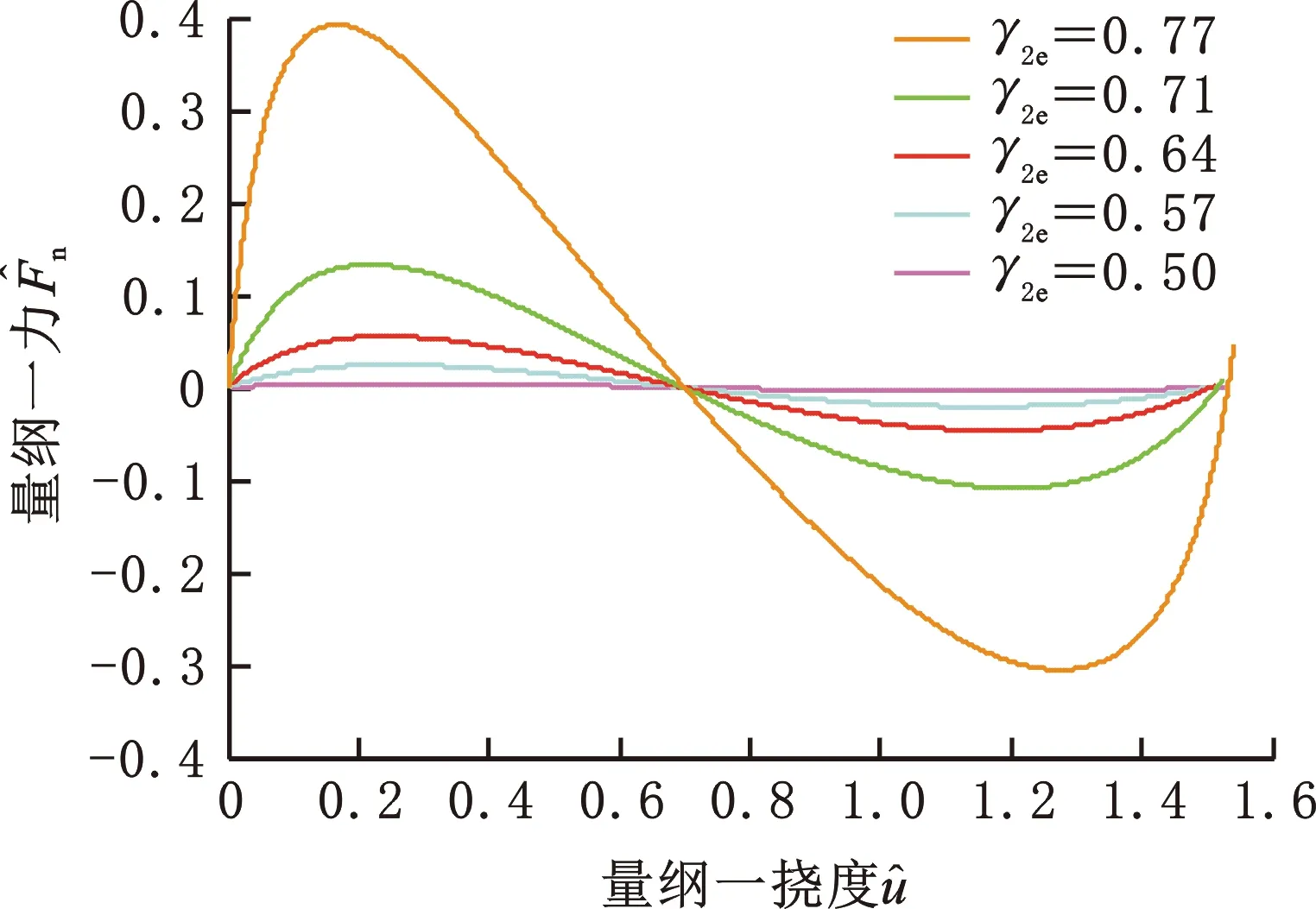
(a)γ2e對的影響

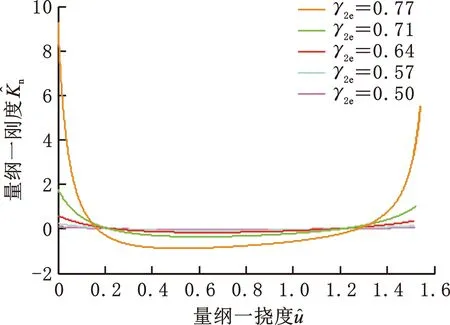
(b)γ2e對的影響圖5 不同γ2e取值時和隨變化曲線Fig.5 The curves of and vs. at different values of γ2e

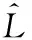
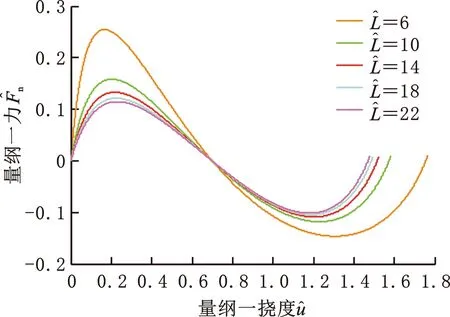
對的影響

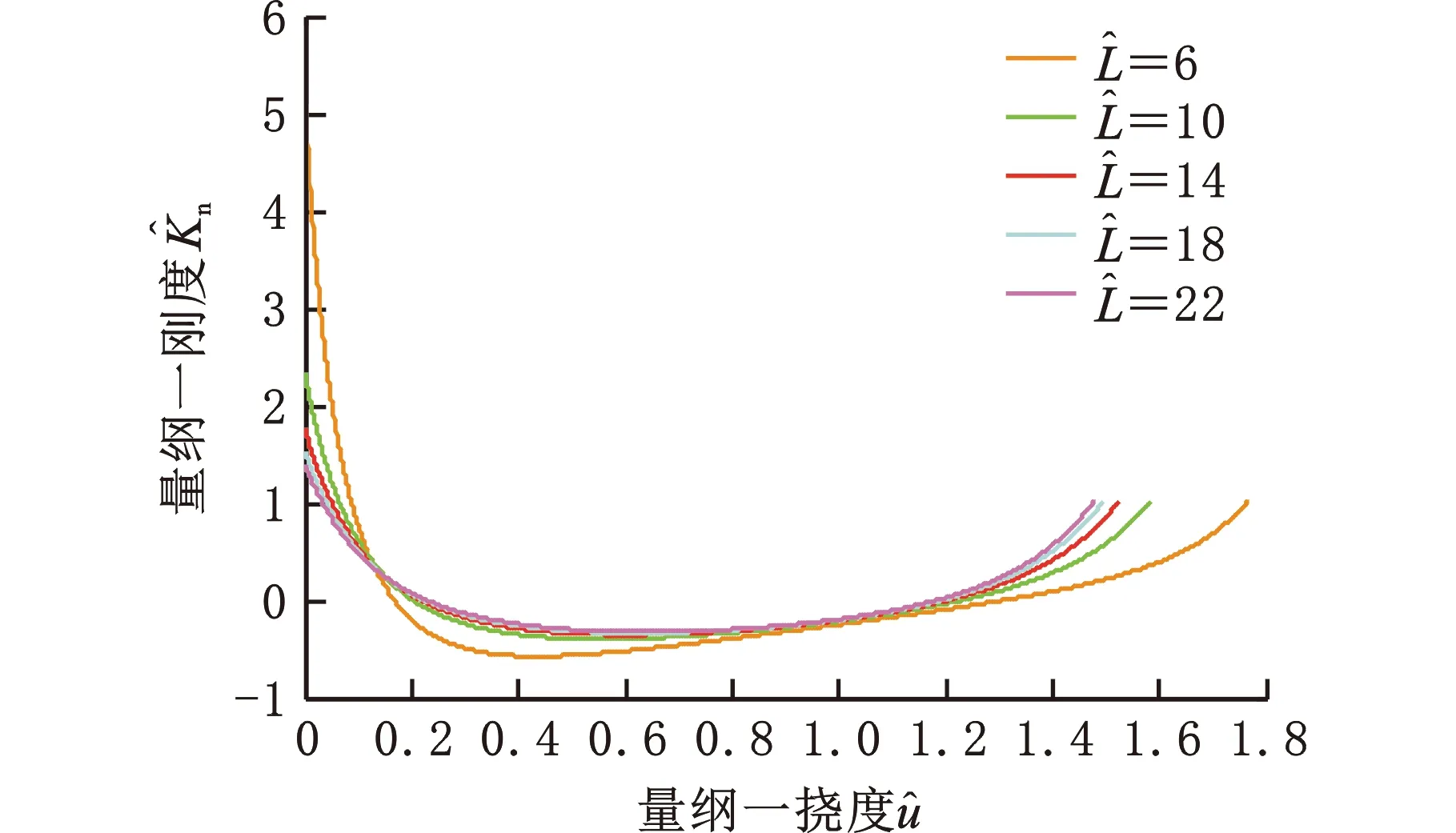
對的影響圖6 不同取值時和隨變化曲線Fig.6 The curves of and vs. at different values of

3.3 低頻振動傳遞特性分析

新型座椅系統是一個強非線性振動系統，故本文采用正弦掃頻方法進行精確求解。基于所建座椅系統動力學模型，在正弦幅值A0分別為3，7，11 mm三種情況下進行掃頻仿真。其中，掃頻間隔為0.02 Hz，掃頻區間為0.1～5.0 Hz，仿真時間設置為120 s。計算每個頻率下加速度穩態輸出與輸入幅值比值，得懸置系統加速度傳遞率T。圖7所示為減振器線性阻尼系數C0=500 N·s/m時不同激振強度下的傳遞率曲線，圖8所示為A0=3 mm時不同C0值下的傳遞率曲線。

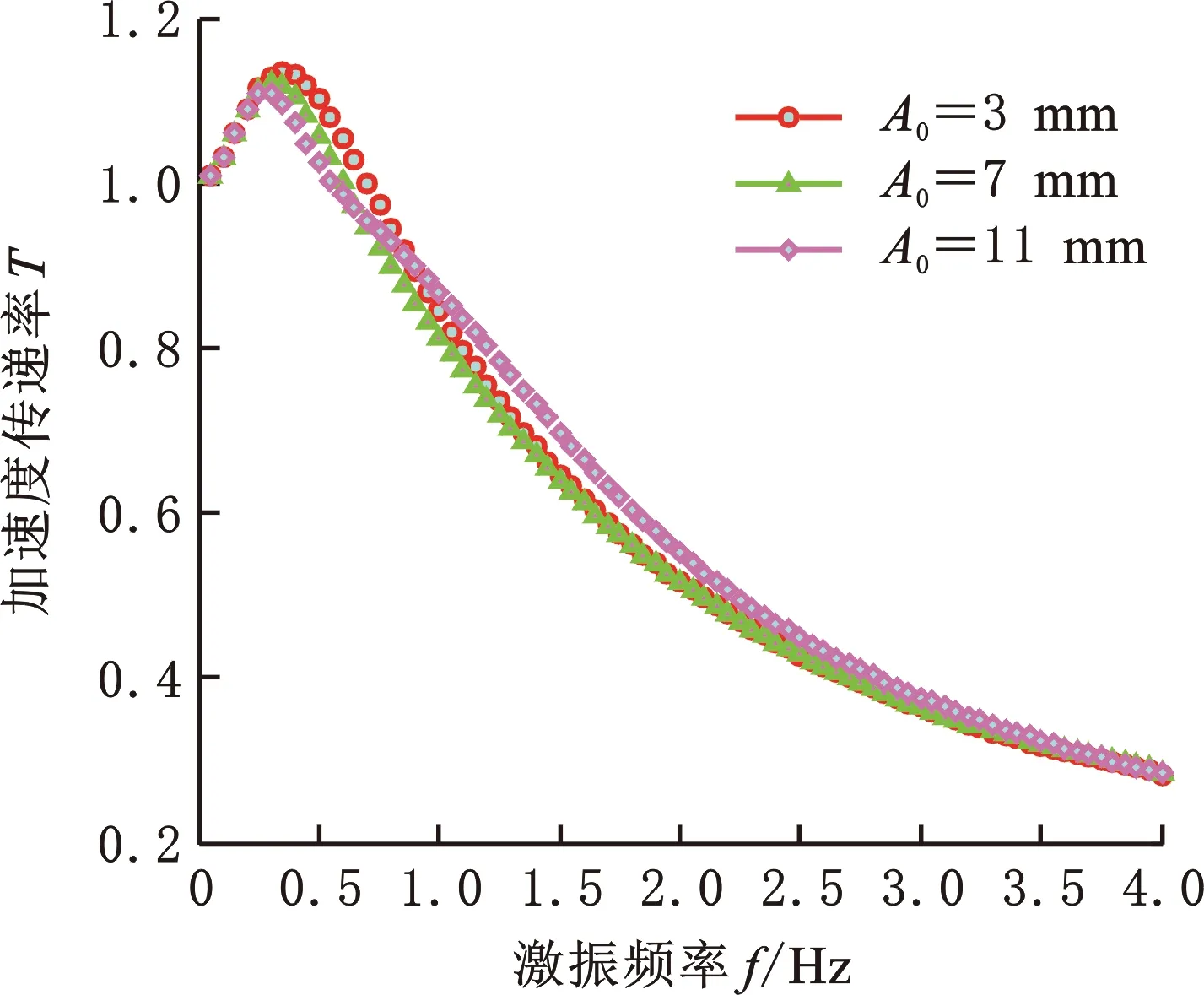
圖7 不同A0時傳遞率T對比Fig.7 A comparison of the transmissibility T at different A0

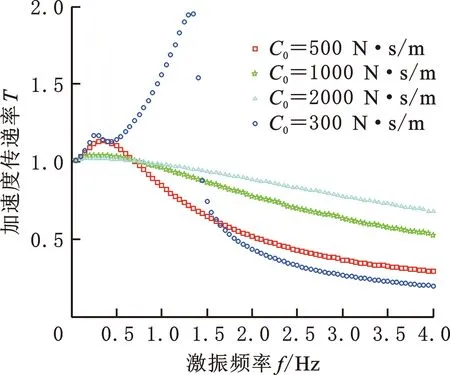
圖8 不同C0時傳遞率T對比Fig.8 A comparison of the transmissibility T at different C0

由圖7可知，當C0=500 N·s/m時，不同激振強度下座椅加速度傳遞率T在0.3～2 Hz低頻區內差異較為明顯，其他區域差異較小。可見，激勵幅值A0對系統振動傳遞特性在低頻區影響較大。分析圖8可知，C0=300 N·s/m時，T曲線有兩個峰值。第一個在0～0.5 Hz范圍內，峰值較小；第二個在1～2 Hz范圍內，峰值較大且發生共振頻率轉移現象，導致系統不穩定。這是由新型懸置座椅系統非線性較強且在靜平衡點兩側剛度不完全對稱而造成的。進一步分析可知，隨著C0值增大，第二個共振峰消失；C0值越大，第一個共振峰值越小，但在非共振區T值明顯增大。綜上，C0值不宜過小或過大。

4 非線性懸置剛度與阻尼優化匹配

在探明新型座椅系統特性影響規律基礎上，建立懸置剛度與阻尼匹配模型并進行實例設計。

4.1 剛度解析匹配模型

4.1.1懸置主彈簧剛度參數匹配

根據座椅承載有效質量m及靜平衡位置時座椅懸置垂向變形量ue，確定新型懸置座椅系統主簧剛度Kv設計值，即

Kv=mg/ue

(23)

Kv值根據質量m額定值確定(此時主彈簧預變形量u0=0)，通過調節主彈簧預變形量u0，可滿足其他質量需求。例如，某駕駛員乘坐后，m比額定值大Δm，則主彈簧預變形量u0可調整為u0=Δmg/Kv。

4.1.2懸置副彈簧剛度參數匹配

主彈簧剛度Kv確定之后，副彈簧剛度Ks將由座椅結構參數、額定載荷位置要求、主簧剛度Kv及等效垂向剛度Ke共同確定。

已知ue和L，根據式(4)，剪桿與座椅底板初始夾角

θ0=arcsin(sinθe+ue/L)

(24)

確定θ0后，根據式(1)，連桿與座椅底板初始夾角

β0=arcsin(h0/r)=

(25)

對前述整體垂向彈性回復力Fte表達式求相對位移u的導數，得等效垂向剛度Ke表達式，即

(26)

式中，χ1、χ2、χ3、χ4均為u的函數表達式。

將式(26)變形并令u=0，則χ1、χ2、χ3、χ4均確定且Kv、θ0及β0已知，此時副簧剛度

(27)

其中，Ke由額定載荷m下靜平衡位置座椅系統要求固有頻率f0確定。

4.2 阻尼匹配數學模型

4.2.1評價指標及其計算方法

根據ISO2631標準，采用座椅面垂向加權加速度均方根aw評價座椅舒適性，其計算式如下：

(28)

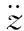
濾波網絡W(f)用如下傳遞函數實現[29]，即

(29)

4.2.2阻尼匹配數學模型構建

為提高座椅振動舒適性，以座椅減振器阻尼參數X(X=(C0，v1f，v1r，γf，γr))為優化設計變量，以aw最小為優化目標，建立目標函數：

(30)

式中，Ω為X設計域。

為避免車輛行駛過程中座椅面與其導軌撞擊，須滿足概率約束條件[30]：

(31)

式中，fd為座椅懸置動撓度；[fd]為座椅懸置限位行程，[fd]=0.03 m；σ(fd)為fd的均方根。

基于目標函數J及約束條件，新型懸置座椅系統阻尼參數匹配數學模型為

(32)

上述數學問題屬于有約束優化問題，可基于文獻[30]提供的流程，采用全局優化算法求解，如遺傳算法、粒子群算法等。

4.3 參數匹配設計實例

為提高某4×2農用車駕乘舒適性[30]，根據額定載荷65 kg下靜平衡位置座椅系固有頻率0.3 Hz及行駛路況要求，為該試驗車輛配置了新型非線性懸置座椅系統并進行了樣機試制。具體設計如下：根據座椅安裝空間要求和結構參數對負剛度機構靜力學特性影響規律，得額定載荷下靜平衡時主簧變形設計值ue=30 mm、剪桿長度L=600 mm、連桿長度r=40 mm。根據剛度解析匹配數學模型，得剪桿與座椅底板初始夾角θ0=49°，連桿與底板初始夾角β0=36°，主簧剛度Kv=20 N/mm、副簧剛度Ks=50 N/mm。基于所建座椅系統動力學模型，以文獻[30]實測砂石路況下試驗車輛座椅底板垂向振動加速度為輸入，利用減振器阻尼匹配方法進行參數匹配，結果為：C0=756 N·s/m，v1f=0.11 m/s，v1r=0.09 m/s，γf=0.71，γr=0.62。加工得到圖9所示的試驗樣機。其中，主簧采用線性螺旋彈簧TF50；副簧為線性螺旋彈簧TF40；主簧可調安裝座采用Q235螺紋鐵管，用于調整主簧預緊變形量u0；連桿采用關節軸承SA12T/K；滾輪采用滾針軸承CF10/KR22。

圖9 試驗樣機Fig.9 The test prototype

5 試驗驗證與能效分析

為驗證所建理論模型和參數匹配方法的正確性并檢驗新型懸置座椅的隔振能力和效果，下文進行了靜力學、掃頻及隨機振動試驗對比分析。

5.1 靜力學試驗對比分析

試驗設備為長春試驗機研究所生產的30 kN綜合試驗臺，如圖10所示，該試驗臺可自動進行數據采集和試驗數據打印。試驗之前，拆除減振器并在各運動副涂潤滑油，將座椅面板與試驗臺架橫梁固定，將座椅底板與試驗臺架的作動器固定；隨后，通過作動器加載并跑合20次，取最后一次數據為最終試驗結果。加載速度對試驗結果影響較大，而本試驗主要目的是測試靜態力下位移-力關系，因此，試驗過程中加載速度設定為5.0 mm/min。試驗測試結果對比如圖11所示。

圖10 座椅靜力學試驗Fig.10 seat static test

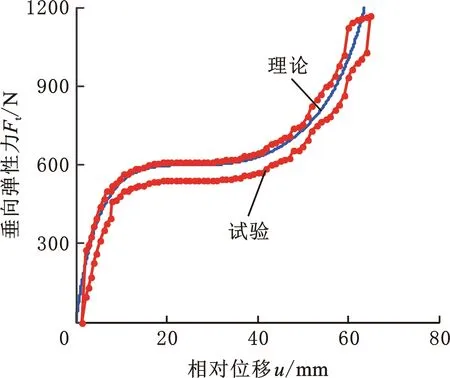
圖11 位移-力曲線對比Fig.11 Ft-u curve comparison

由圖11可知，u-Ft試驗曲線與理論設計曲線平直段吻合較好，其他部分存有一定差異。對比結果表明，所建新型懸置座椅位移-力靜力學模型能夠較好地反映懸置系統真實靜力學特性。曲線存有差異主要是運動副存在間隙和干摩擦且試驗樣機加工尺寸有一定偏差所致。此外，因干摩擦導致卸載試驗曲線呈現滯回現象。

5.2 掃頻試驗對比分析

用65 kg配重代替駕駛員并固定在新型座椅面上，在綜合試驗臺施加幅值為6.0 mm的正弦激勵以進行掃頻試驗；然后，拆除副簧和連桿，將新型座椅轉換為傳統剪式線性機械座椅并進行掃頻試驗。其中，掃頻間隔為0.05 Hz，掃頻區間為0.1～6 Hz。圖12所示為加速度傳遞率試驗與仿真對比曲線。

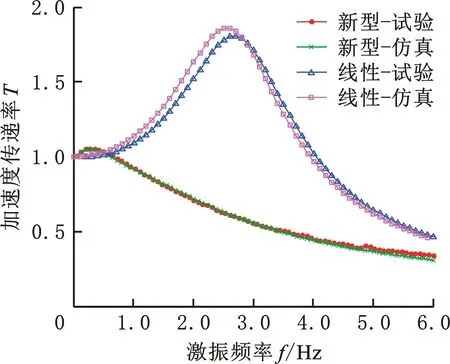
圖12 加速度傳遞率試驗與仿真曲線對比Fig.12 A comparison of T curves between the test and the simulation

由圖12可知，新型座椅加速度傳遞率仿真與試驗曲線吻合較好，兩者在0～4 Hz幾乎重合，僅在4～6 Hz略有差異。結果驗證了所建新型座椅系統動力學模型的正確性。與傳統剪式線性機械座椅相比，新型座椅最大傳遞率和固有頻率分別降低了31.2%和80.6%，對比結果表明新型座椅隔振性能明顯優于線性座椅。

此外，因試驗中線性座椅由新型座椅拆除副簧而來，拆除副簧后負剛度機構摩擦力幾乎消失，故線性座椅T試驗曲線比新型座椅的更光滑。對比結果也說明，新型座椅若副簧失效，可提供傳統剪式線性座椅隔振性能，確保性能不嚴重惡化，從而提高新型懸置座椅系統實用性和可靠性。

5.3 隨機振動試驗對比分析

為進一步對比驗證新型非線性座椅減振性能，將前期試驗所測砂石和瀝青兩種路況下座椅底板加速度轉換為位移信號[30]，以此驅動綜合試驗臺作動器，分別對新型非線性座椅、傳統非線性座椅及傳統線性座椅施加振動激勵，進行隨機振動試驗，如圖13所示。同時，為對比分析非線性懸置座椅系統失效情況下隔振性能，將新型非線性座椅副簧拆除，將傳統非線性座椅其中一側副簧拆除，復現實際工程中最常見失效形式并分別進行試驗。試驗之前拆除各座墊，消除坐墊對座椅性能對比的干擾。瀝青路況下新型非線性座椅垂向加速度試驗與仿真時間歷程對比如圖14所示，不同座椅垂向加權加速度均方根aw及懸置動撓度均方根σ對比如表3所示。

圖13 隨機振動試驗Fig.13 The random test

圖14 加速度對比Fig.14 Acceleration comparison

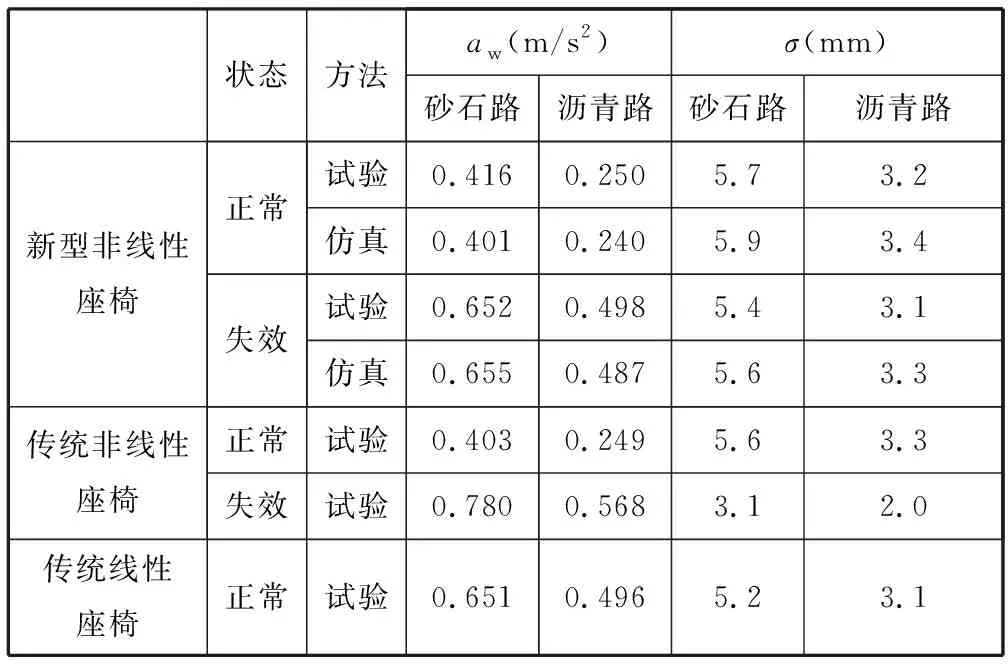
表3 座椅減振性能對比Tab.3 A comparison of the seat performance

由圖14可知，瀝青路況下新型非線性座椅垂向加速度試驗與仿真時間歷程吻合較好，表明所建座椅系統動力學模型能有效復現座椅在隨機路況下的真實動力學響應。分析表3可知，砂石和瀝青兩種路況下新型非線性座椅垂向加權加速度均方根aw仿真值與試驗值相對偏差分別為3.6%和4.0%，懸置動撓度均方根σ仿真值和試驗值相對偏差分別為3.5%和6.3%，對比結果進一步驗證了所建動力學模型的正確性。誤差主要是由所建座椅系統動力學模型沒有考慮運動副摩擦和間隙造成的。

進一步分析表3可知，正常工作狀態下，兩種路況下新型非線性座椅的σ值和aw值與傳統非線性座椅的相當；與傳統線性座椅相比，雖然新型非線性座椅的σ值略有增大，但砂石和瀝青路況下aw值分別降低了36.0%和49.6%。在失效狀態下，與傳統線性座椅相比，兩種路況下傳統非線性的aw值分別增大了19.8%和14.5%，而新型非線性座椅的σ值僅分別增大了0.2%和0.4%。可見，正常工作下新型非線性座椅減振性能與傳統非線性座椅相當，但失效狀態下新型非線性座椅減振性能與傳統線性座椅相當，且明顯優于傳統非線性座椅。進一步分析可知，因失效狀態下，新型非線性座椅轉化為了傳統線性座椅，故其性能沒有嚴重惡化；而傳統非線性座椅在橫置副簧側向力作用下導致座椅垂向運動產生一定卡滯，故σ值明顯減小且aw值增大。

綜上分析，與傳統線性座椅相比，新型非線性座椅振動舒適性顯著提高且與傳統非線性座椅相當；與傳統非線性座椅相比，新型非線性座椅不僅結構簡單、成本低、便于工程上實現高低選配，而且使用可靠性更高。

6 結論

(1)基于新型負剛度隔振機構揭示了新型非線性座椅提高使用可靠性、降低生產成本的原因并闡明了其工作原理，建立了基于準零剛度理論的座椅懸置系統彈性力解析表達式、量綱一位移-剛度數學模型及非線性系統動力學模型。

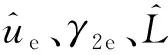
(3)提出了座椅非線性懸置剛度解析匹配方法，構建了減振器非線性阻尼匹配數學模型，設計加工了樣機并進行了試驗驗證，結果驗證了所建靜力學模型、動力學模型、參數匹配模型及方法的正確性和有效性。

(4)試驗分析結果表明：與傳統線性座椅相比，新型非線性座椅振動舒適性顯著提高且與傳統非線性座椅相當；與傳統非線性座椅相比，新型非線性座椅成本更低且使用可靠性更高。