miniSAR 衛星精密參考軌道設計

廖祥, 鄭靖, 許永生, 謝成清, 丁強強

(1. 深圳市魔方衛星科技有限公司, 深圳 518129; 2. 深圳航天東方紅衛星有限公司, 深圳 518057)

2015 年以來,多個國外商業航天初創公司相繼提出并部署各自的輕小型合成孔徑雷達(mini synthetic aperture radar,miniSAR)衛 星[1]。 在 此背景下,深圳航天東方紅衛星有限公司瞄準市場前景廣闊的高分辨率微波成像和形變測量應用領域的miniSAR 衛星項目,并立項研發,計劃2021年底具備發射條件。 為實現高精度長時間序列的形變監測,miniSAR 衛星的重軌干涉基線設計優于500 m,要求衛星在軌任務期間的三維空間回歸軌跡被控制在直徑為500 m 的管道內。

管道指以衛星運行軌道的參考軌跡為中心、干涉基線極大值為直徑的三維空間[2]。 以國外早期干涉SAR 衛星項目為例,ERS-1/ERS-2 管道設計直徑為600 m[3],TerraSAR-X 為500 m[4],ALOS/ALOS-2 為1000 m[5],Sentinel-1 則 達 到 了150 m[6-7]。 由于SAR 衛星一般運行在500 ～800 km高度范圍內的低地球軌道空間,大氣阻力與太陽光壓等非保守攝動力會對衛星軌道根數造成長期影響,如此高精度的管道控制要求,需設計高精度參考軌跡為基準,進一步實施精密軌道控制[8]。而參考軌跡由參考軌道預報一個回歸周期生成,因此,干涉SAR 衛星高精度軌道控制中一個十分重要的術語“參考軌道”被提出。

參考軌道指在僅考慮中心天體保守力情況下,滿足預報一個回歸周期后衛星地固系下的三維空間位置完成重合的一類軌道。 參考軌道僅為一組包含歷元的軌道根數,其最終類型為瞬時軌道根數(又稱密切軌道根數),坐標系通常為慣性系瞬時真赤道地心坐標系(true of date,TOD)[9]。對于需要生成長期一致的時間序列干涉數據的SAR 衛星,參考軌道一旦完成設計,在整個任務周期內就不能更改,這同時對重軌單星和雙星近距編隊干涉SAR 系統構成約束。

由于干涉SAR 衛星技術起步較晚,且工程任務較少,國內外關于參考軌道設計的文獻較欠缺。推導嚴密、可復現性好的精密參考軌道設計文獻更是稀缺。 文獻[10]針對TerraSAR-X 任務,實現了一種基于虛擬速度增量與序列二次規劃的參考軌道優化設計方法,但由于引入了2 次虛擬軌控,生成的參考軌跡不連續;文獻[11]提出基于迭代修正方法的嚴格回歸軌道設計,但文中的推導存在部分錯誤,實現算法存在缺陷,且回歸精度較差;文獻[12]提出一種基于高階地球重力場模型的嚴格回歸軌道單目標優化設計方法,但回歸精度較差,仍在米級;文獻[13]在修正文獻[10]方法的同時,解決了利用傾角偏置修正沿跡向長期漂移的問題,但文中采用專有工具優化設計參考軌道,無法獲取具體實現算法。

本文基于嵌套式迭代修正思想,通過合理選擇參考系、初始預估參數、平根與軌道外推模型,并合理設置迭代修正反饋值及迭代收斂判據,建立了一套推導嚴密、可復現性好的miniSAR 衛星精密參考軌道設計算法,由其設計的參考軌道生成的參考軌跡在地固系下的閉環精度達毫米級。

1 參考軌道特性分析

miniSAR 衛星的參考軌道必須同時具備2 個基本特性:①軌道必須是回歸軌道,即運行在該軌道上的衛星對星下點具有高精度重訪特性;②軌道必須是凍結軌道,即衛星星下點重訪時軌道高度的一致性。 根據軌道動力學原理,回歸軌道特性與軌道半長軸a和傾角i相對應,凍結軌道特性與偏心率e和近地點幅角ω相對應[10]。

此外,考慮到衛星能源的穩定性及升交點赤經的進動速率,miniSAR 衛星的參考軌道還設計具備太陽同步軌道特性。 這一特性進一步約束了參考軌道半長軸a和傾角i之間的關系[14]。

1.1 太陽同步特性

太陽同步軌道平面法線與太陽矢量在赤道平面上的投影保持著固定的夾角關系,這使得運行其上的衛星可獲得穩定的光照條件,且在衛星飛越相同地理緯度的目標區域處于同一地方時。 太陽同步軌道的設計主要考慮降交點平地方時(mean local time, MLT)與平均軌道高度(mean orbit altitude, MOA)2 個參數。

文獻[15]指出,太陽同步軌道傾角平根受太陽引力影響的長期攝動年變化率di/dt(°/年)與降交點MLT 成正弦關系,降交點MLT 為3:00、9:00、15:00、21:00 時di/dt最 大,降 交 點MLT 為0:00、6:00、12:00、18:00 時di/dt最小并接近于0,如圖1 所示。 因此,在設計太陽同步軌道參數時,干涉SAR 衛星適合選擇0:00、6:00、12:00、18:00 附近的降交點MLT,以減小傾角平根的長期漂移,進而避免不必要的傾角調整。

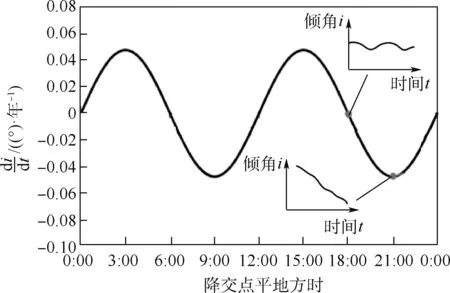
圖1 受太陽引力影響的傾角長期項攝動[15]Fig.1 Secular perturbation of inclination due to gravity of the Sun[15]

MOA 的設計則需考慮SAR 衛星載荷在一個回歸周期T內可實現對全球的無縫覆蓋。 這里的覆蓋能力并非實際可照射區域,而是衛星在姿態最大側擺角下載荷所能覆蓋的區域來計算。 由于SAR 載荷一般具有照射盲區,因而MOA 的設計需要對此因素加以建模分析。

確定好降交點MLT 與MOA 后,可根據基于J2低階引力攝動下的太陽同步軌道設計方程進一步確定軌道傾角:

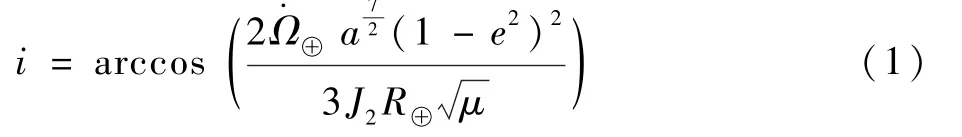
式中:μ為地球引力常數;R⊕為地球平均半徑;為地球公轉升交點赤經進動速率;J2為地球非球形引力模型二階帶諧項系數。

1.2 回歸特性

理想的參考軌跡在地固系三維空間下為首尾完全閉合的曲線,因而參考軌道必須具有回歸特性。 給定回歸周期T與對應的回歸圈數N,則回歸軌道約束方程為

式中:ω⊕為地球自轉速率;分別為升交點赤經、近地點幅角、平近點角的進動速率,三者在J2低階引力攝動下的解析式[16]為

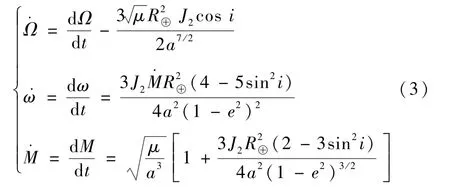
式中:傾角i以式(1)為約束參與式(3)對半長軸a的求解;Ω為升交點赤經;ω為近地點幅角;M為平近點角。

1.3 凍結特性

理想參考軌跡的星下點重訪時軌道高度保持不變,因而參考軌道必須具有凍結特性。 凍結軌道有2 種類型:①臨界傾角的凍結軌道;②小偏心率近圓凍結軌道。 干涉SAR 衛星的參考軌道屬于第2 種情況。 凍結軌道設計方程為

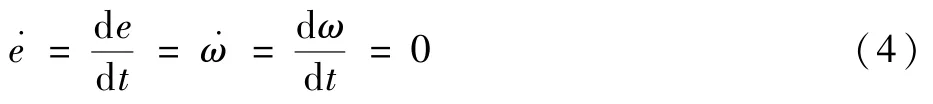
根據小偏心率近圓凍結軌道的要求,考慮J2及J3低階引力攝動可解算得到

式中:J3為地球非球形引力模型三階帶諧項系數。

1.4 參考軌道預估值

綜上對參考軌道特性的分析,可預估得到5 個基于低階引力勢場的參考軌道根數:

需要指明的是,此處獲得的參考軌道初值為TOD 坐標系下的平根,在使用之前須將其轉換為瞬根方可作為初始輸入參與后續迭代修正過程:

式中:a0、i0、e0、ω0、M0分別為半長軸、傾角、偏心率、近地點幅角、平近點角的瞬根。

2 參考軌道設計算法

參考軌道的設計包含兩部分工作:①針對(a,i)組合的太陽同步回歸軌道的優化設計;②針對(e,ω)組合的凍結軌道的優化設計。 但由于(a,i)迭代修正的輸入為預估的參考軌道根數,2種組合優化設計方法需嵌套使用。 當(e,ω)迭代收斂之后,只需再重復一輪(a,i)迭代修正即可實現高精度回歸。 具體算法流程如圖2 所示。

圖2 精密參考軌道設計算法流程Fig.2 Algorithm flow chart of precise reference orbit design

2.1 迭代修正具體實現

從算法流程可見,參考軌道設計過程主要分為3 個步驟:①(a,i)組合迭代粗修正;②(e,ω)組合迭代修正;③(a,i)組合迭代精修正。

2.1.1 (a,i)組合迭代粗修正

(a,i)組合迭代粗修正以參考軌道初值a0為輸入,外推1 個回歸周期T,利用首尾軌道數據生成平根修正量(Δˉa,Δˉi),并進一步通過平瞬轉換獲得新的(a,i)值,其余軌道根數保持不變。 其中,(ˉ)為實際獲得的平根修正量,(a,i)則為最終修正得到的瞬根值。 ()根據梯度矩陣獲得

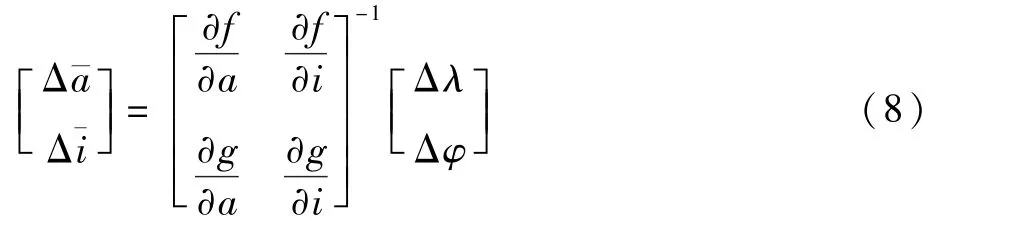
式中:Δλ和Δφ分別為首尾軌道數據星下點經緯度之差;4 個偏導數求解式為

其中:中間量?u/?a計算如下:

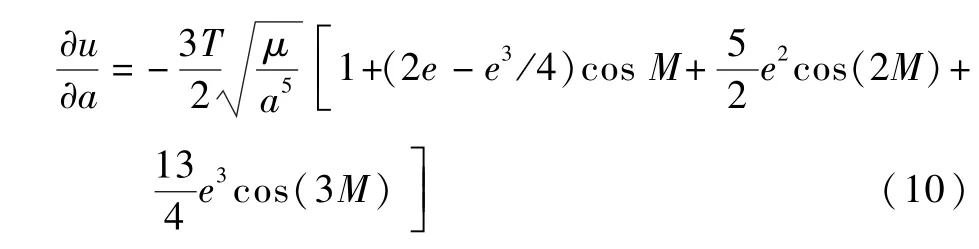
式(8) ～式(10)為最終算法,其詳細推導過程可參考文獻[10-12],但注意式(9)對文獻[11]中錯誤部分的更正。

2.1.2 (e,ω)組合迭代修正

圖3 偏心率平根矢量修正示意圖Fig.3 Diagram of mean eccentricity vector correction

2.1.3 (a,i)組合迭代精修正

(a,i)組合迭代精修正的實施方法與2.2 節

步驟1相同,但本節迭代修正的收斂判據與2.2 節步驟1 不同。

2.2 收斂判據

(a,i)與(e,ω)組合每輪修正需要多次迭代實現收斂,參考軌道設計算法的3 輪組合修正都需要給定明確的收斂判據,用以判斷每次迭代后的結果是否滿足收斂條件,各輪修正的收斂判據如下。

步驟1判定3。 以前后2 次迭代修正后的參考軌道根數,預報1 個回歸周期T之后的三維空間軌跡回歸精度優于精密定軌精度為收斂準則。 參考GNSS 精密定軌精度為厘米級,故收斂準則設置為

式中:n為迭代次數,n≥1;為參考軌跡閉環回歸精度,計算式為

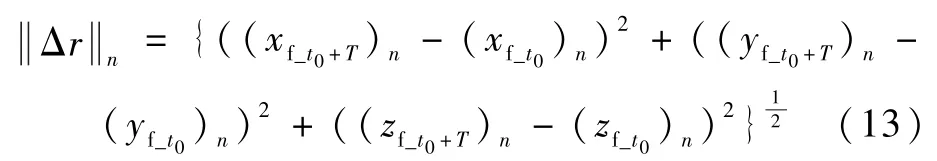
式中:xf、yf、zf分別為地固系三維坐標值,時間下標t0、t0+T表征預報1 個回歸周期T所得軌道數據的首、尾坐標值。

步驟2判定2。 以前后2 次迭代修正后的偏心率平根矢量偏差引起的參考軌跡偏差ˉaΔˉe優于厘米級為收斂準則。 由于ˉa為10-6m量級,故偏心率平根矢量前后差異需優于1.0 ×10-8,即

步驟3判定1。 以前后2 次迭代修正后的參考軌道根數預報1 個回歸周期T之后的三維空間軌跡回歸精度無明顯提高為收斂準則。 考慮二階展開,回歸精度差異需優于o(),即

式中:abs()表示取絕對值;n為迭代次數,n≥2。

2.3 平瞬轉換

參考軌道設計算法的迭代實際修正量為平根,但參考軌道的形式為瞬根,因此在修正平根后需執行平瞬轉換獲得瞬根修正值。

常用的平瞬轉換模型有多種[16],本文選用考慮J2～J6及攝動的Eckstein-Hechler 模型[17],該模型專門針對小偏心率凍結軌道進行優化,尤其適合參考軌道設計過程。

Eckstein-Hechler 模型在基于SCILAB 科學計算語言的Celestlab[18]與基于Java 語言的Orekit[19]這2 套成熟開源航天動力學庫中皆有實現,可作為實現參考。

2.4 外推模型

(a,i)與(e,ω)組合迭代修正的過程皆需要進行軌道外推,以獲得向后一段時間的軌道數據。由于參考軌道只考慮中心天體保守力,因而外推模型的動力學只考慮高階地球非球形引力,本文為100 ×100 階的EGM2008 引力模型[20]。

動力學模型的單一決定了外推模型的精度取決于積分器的選擇及對積分步長的控制。 考慮到積分效率與精度,選擇9 階誤差控制的8 階Runge-Kutta-Verner 積分器RKV8(9)[21]。 修正過程中,誤差容限設為優于1.0 ×10-13,(a,i)、(e,ω)組合迭代修正最大步長分別控制在10 s、5 s 以內。

3 數值實驗

3.1 輸入數據與實驗條件

3.1.1 軌道特性輸入

miniSAR 衛星軌道設計為具有10 天/151 軌(回歸周期為10 天,10 天內衛星運行151 軌)回歸、凍結特性的太陽同步軌道,標稱降交點MLT為6:00(晨昏軌道),衛星質量為180 kg。

3.1.2 定位數據輸入

衛星成功入軌后經運控系統提供一組包含升交點的定位數據,如表1 所示(表中為仿真的地固系三維位置與速度值)。 對其插值得到升交點處地固系狀態矢量,對應歷元t0為2021-01-01,00:26:13.511 668 UTCG。 再利用升交點處的地固狀態矢量計算得到升交點赤經平根初值為=10.881 803 934°。

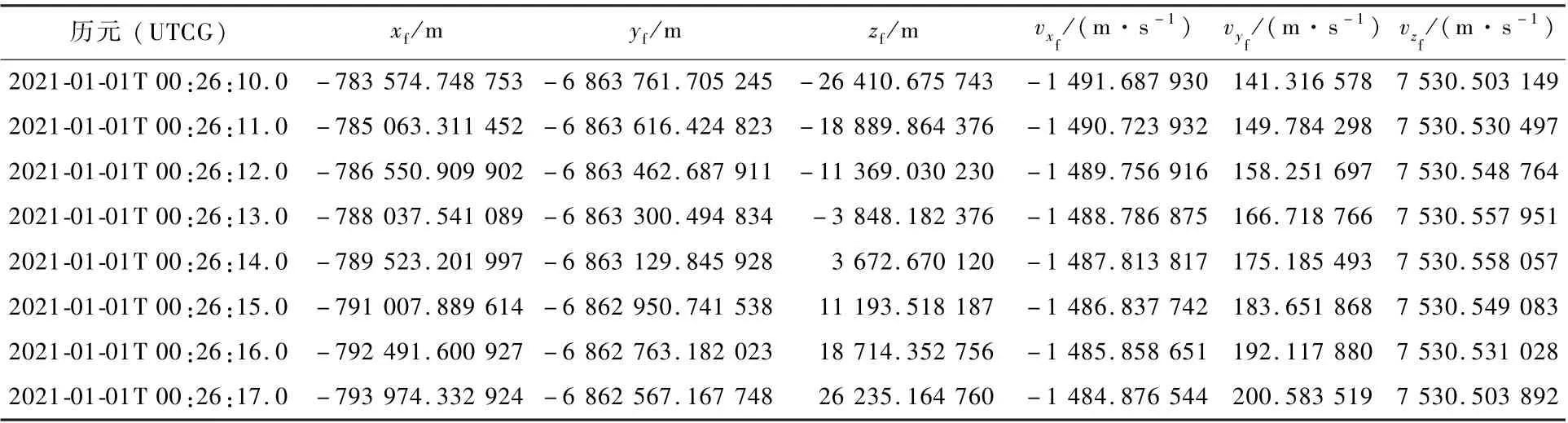
表1 定位數據Table 1 Precision positioning data

3.1.3 參考軌道初值

根據軌道特性預估值與定位數據,計算得到的參考軌道在t0時刻的初值為

平瞬轉換后參與迭代修正的參考軌道初值為

3.1.4 實驗條件

數值實驗基于MATLAB 語言環境,軌道外推與數據報表使用STK Engine 的MATLAB 編程接口實現,平瞬轉換算法移植自Celestlab。 仿真程序運行于搭載Windows 10 專業版操作系統的聯想P52 移動工作站,機帶內存32 GB,處理器型號為Intel Xeon E-2176M。

3.2 實驗結果

表2 給出了參考軌道初值及數值實驗過程中3 輪迭代修正所得參考軌道根數,其中a為最終獲得的參考軌道根數。 從表2 中數據可見,由a0到a1及a2到a的過程中,只有半長軸與傾角是變化量;由a1到a2的過程中,只有偏心率、近地點幅角與平近點角是變化量。

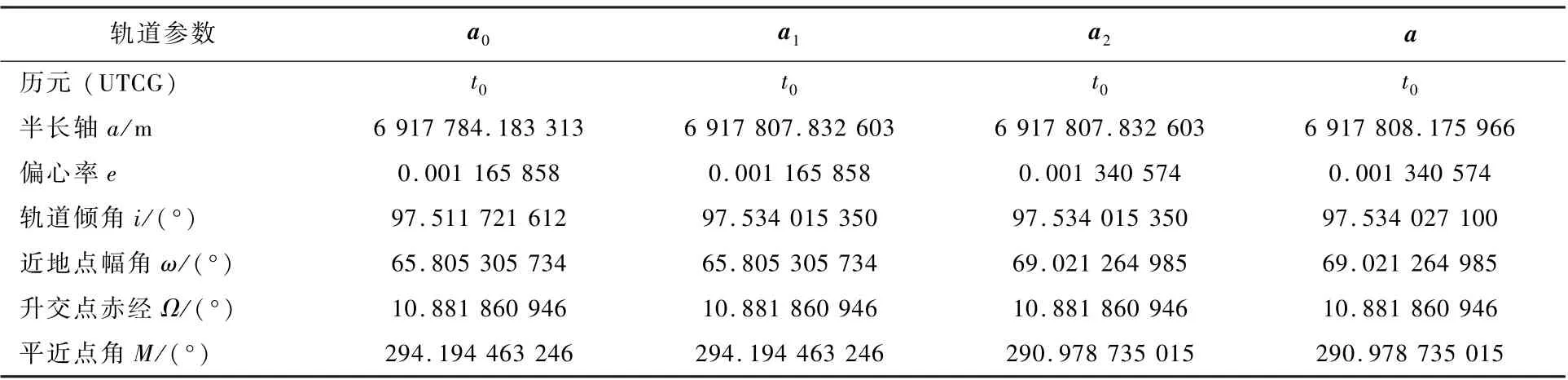
表2 迭代修正過程中所得參考軌道根數(TOD 瞬根)Table 2 Reference orbit elements obtained during process of iterative correction (TOD osculating elements)

表3 給出了3 輪修正迭代過程中收斂判據的統計數據,圖4 ～圖7 則對統計數據進行了可視化。 其中,圖4 與圖5 對應第1、2 輪(a,i)組合迭代修正過程中的收斂情況,橫坐標n為迭代次數,圖6 與圖7 則對應(e,ω)組合迭代修正過程中偏心率平根矢量收斂情況。 統計數據表明:

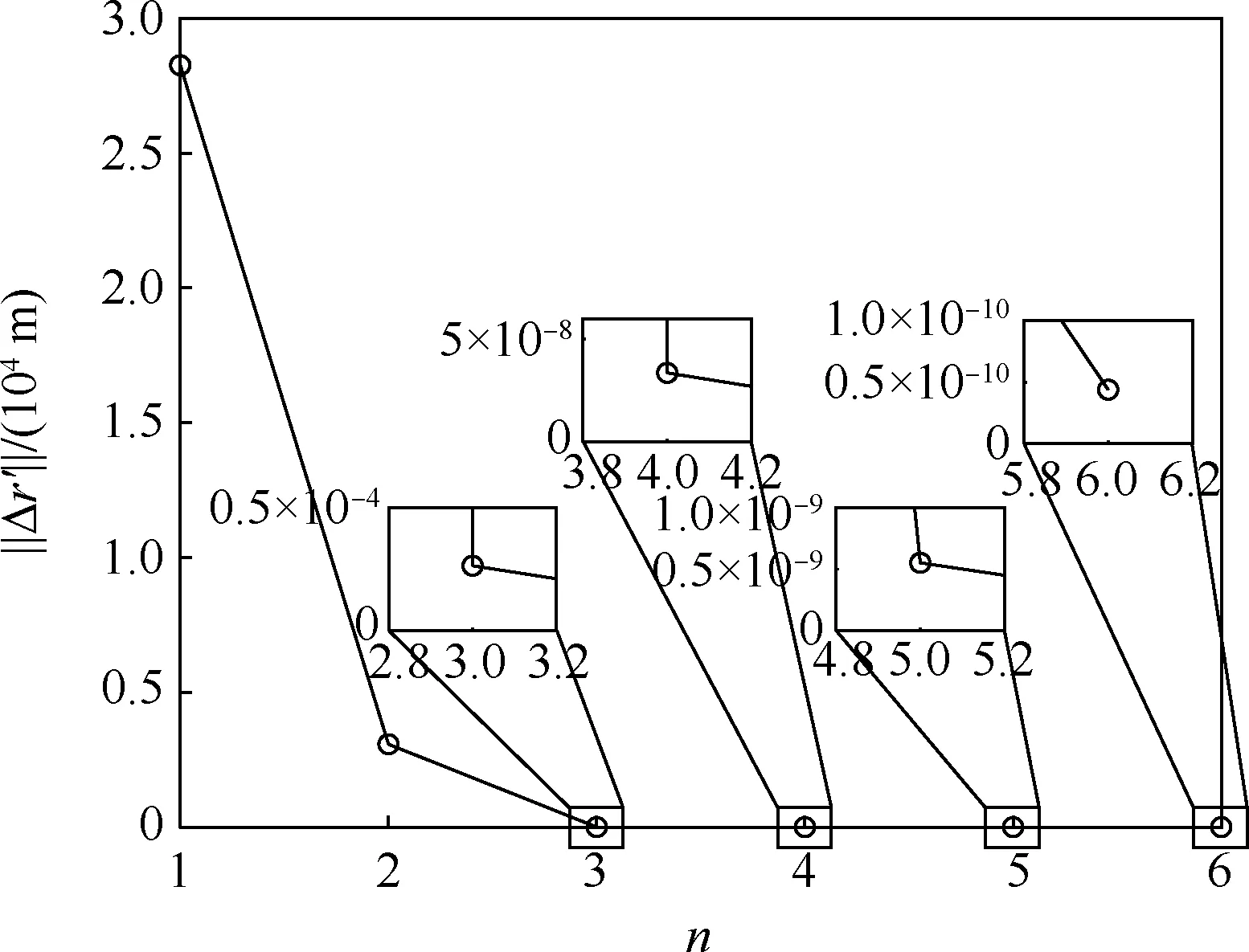
圖4 第1 輪(a,i) 迭代修正收斂情況Fig.4 Convergence of first (a,i) iterative correction

圖5 第2 輪(a,i) 迭代修正收斂情況Fig.5 Convergence of second (a,i) iterative correction

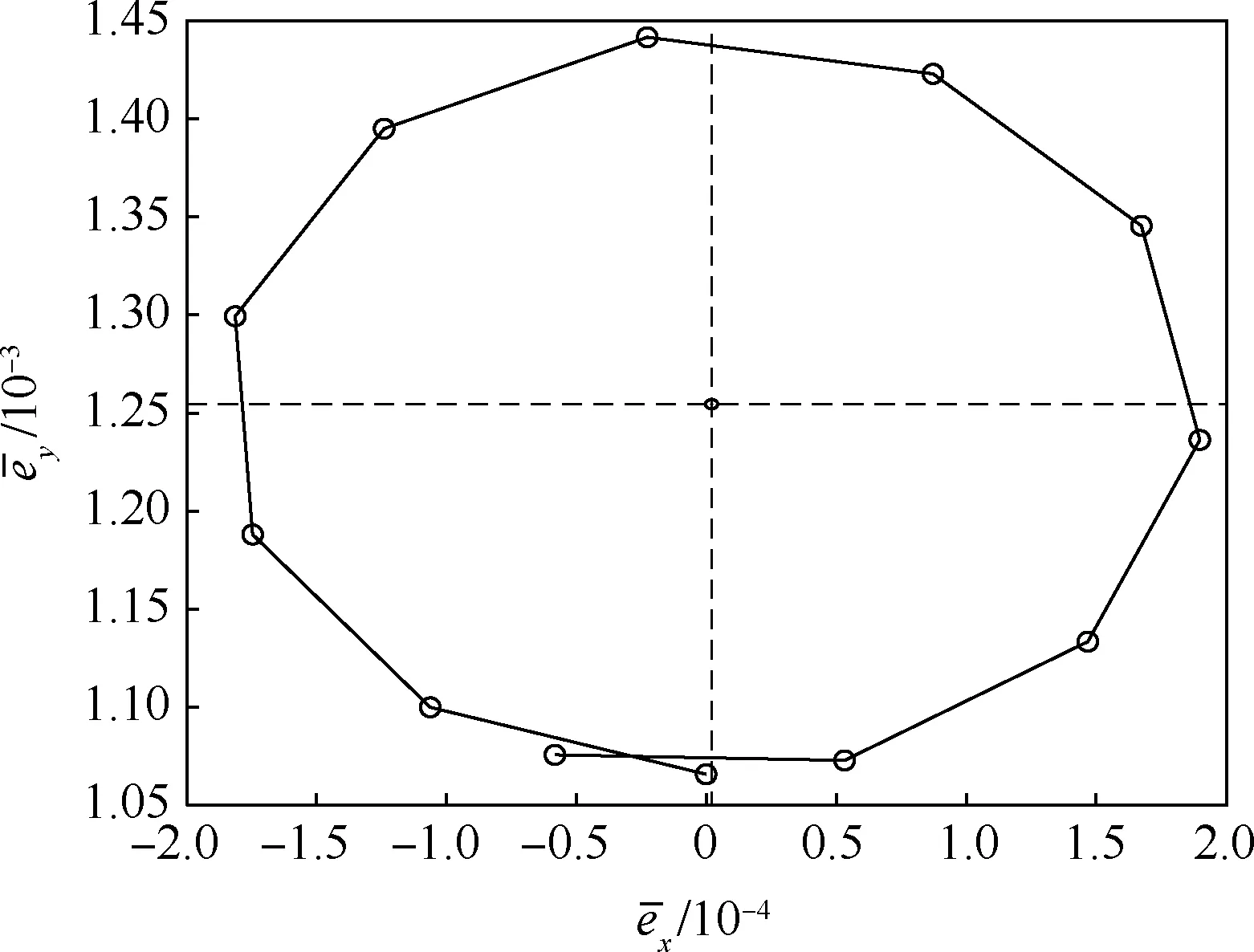
圖6 偏心率平根矢量收斂情況Fig.6 Convergence of mean eccentricity vector

圖7 (e,ω)迭代修正收斂情況Fig.7 Convergence of (e,ω) iterative correction

表3 迭代修正收斂數據Table 3 Convergence data of iterative correction

1) 第1 輪(a,i)組合迭代修正過程中,僅6 次迭代即實現收斂,收斂精度達4.38 ×10-7m。

2) (e,ω)組合迭代修正過程中,120 天內以1 個回歸周期為步長的偏心率平根矢量在迭代修正過程中逐步收縮半徑,僅4 次迭代偏心率平根變化率Δˉe即收斂至2 ×10-10。

3) 第2 輪(a,i)組合迭代修正過程中,僅4 次迭代即實現收斂,收斂精度優于0.006 m。

綜合本節所述,實驗結果的收斂精度滿足收斂判據指標,驗證了所提miniSAR 衛星參考軌道迭代修正設計算法的有效性和精密性。

實驗中,單次(a,i)修正平均耗時56.64 s,單次(e,ω)修正平均耗時624.45 s,合計耗時47.29 min。衛星軌控任務周期一般大于軌道周期,合計耗時小于miniSAR 衛星約95.36 min 的軌道周期,不影響軌控任務正常開展。 此外,考慮到軟硬件條件,參考軌道設計工作不適合在內存低于GB 級的嵌入式星載計算機上進行。

4 結 論

本文建立了一套完整的miniSAR 衛星精密參考軌道設計算法,經過嵌套式(a,i)、(e,ω)組合的3 輪迭代修正獲得了毫米級三維空間軌跡回歸精度。

1) 引入了參考軌道的具體定義,提出的參考軌道設計算法流程清晰、推導嚴密、收斂判據明確、可復現性好。

2) 提升了參考軌道設計速度與精度,數值實驗在48 min 內獲得了地固系三維空間閉環回歸精度約為0.005 m 優于0.01 m 的精密參考軌道,滿足實際工程應用需求。