圍繞主題漸次生長:數學習題課的教學追求
——以蘇科版數學九(下)“二次函數”習題課教學為例
■姜國生
二次函數是九年級的重點內容,新授課之后往往要安排必要的習題課進行鞏固訓練,如果教師選擇的習題比較零散,則不利于學生掌握同一類問題。因此,筆者圍繞二次項系數為1的二次函數問題研發了一節習題課,在教研組內執教公開課后,取得較好的課堂效果,也獲得組內同行的好評。下面,筆者整理本節課教學設計,并給出教學立意的闡釋,供同行們研討。
一、教學設計
1.基礎熱身
例1如圖1,已知拋物線y=x2。
(1)在圖1中,求拋物線y=x2與直線y=1的兩個公共點坐標;
(2)在圖1中,求拋物線y=x2與直線y=4的兩個公共點之間的距離;
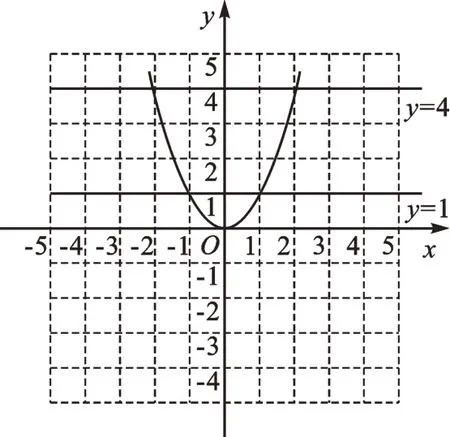
圖1
(3)在圖2中,求拋物線y=(x-1)2與直線y=4的兩個公共點之間的距離;
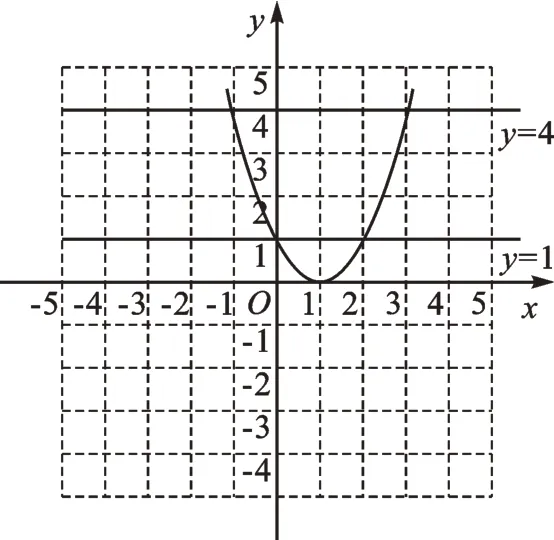
圖2
(4)在圖3中,求拋物線y=-(x+2)2+2與直線y=-2的兩個公共點之間的距離。

圖3
[設計意圖]通過上述4個題目,學生對二次項系數為1的二次函數圖像的形狀特征更加熟悉,為后續的變式應用奠定基礎。
變式1在平面直角坐標系xOy中,二次函數y=x2+mx+n的對稱軸為直線x=2,且經過點A(0,3)。將這個二次函數的圖像沿y軸向下平移,請問:當向下平移幾個單位時,所得到的新的函數圖像與x軸的兩個交點之間的距離為4。
[設計意圖]有些學生先寫出二次函數表達式y=x2-4x+3。教師要引導學生寫成頂點式y=(x-2)2-1,讓學生結合例1積累的圖像特征,得到新的函數圖像與x軸的兩個公共點之間的距離。
2.拾級而上
例2如圖4,已知正方形OBCD的三個頂點坐標分別為B(1,0)、C(1,1)、D(0,1)。試分析拋物線y=(x-h)2(h為常數)與正方形OBCD的邊的公共點個數,并指出相應的h的取值范圍。

圖4
[設計意圖]教師通過追問的方式,引導學生自主梳理不同的臨界情形對應的公共點個數,讓學生明白本題的本質就是拋物線y=(x-h)2(h為常數)的頂點在x軸上平移。
變式2已知M(x1,y1)、N(x1,y1)為拋物線y=ax2(a≠0)上任意兩點,其中0≤x1<x2。若對于x2-x1=1,都 有|y1-y2|≥1,則a的 取 值 范 圍 為__________。
[設計意圖]變式2主要是針對例2的變式訓練與學情反饋。首先,教師要引導學生學會利用“以形助數”進行分析,構造出圖5。然后引導學生分情況討論,其中包括當a>0時,對于x2-x1=1,都有|y1-y2|≥1,所以a|x12-x22|≥1,解得a≥1。同理,當a<0時,解得a≤-1。最后得出a≥1或a≤-1。
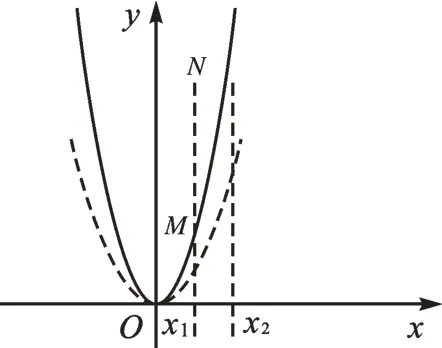
圖5
3.拓展提升
例3在平面直角坐標系xOy中,已知拋物線y=x2-2mx+m2-1。直 線y=-x+b與x軸交于點A(3,0),與y軸交于點B,過點B作垂直于y軸的直線l交拋物線于點P、Q,若△OAP和△OAQ中有且僅有一個為鈍角三角形,結合圖像,求m的取值范圍。
[設計意圖]教師引導學生將拋物線表達式改寫成頂點式y=(x-m)2-1,讓學生能看出該拋物線的平移規律,求出一次函數表達式y=-x+3。此時再構造圖6、圖7這兩種臨界情形,教師鼓勵學生結合圖形自主分析講解。

圖6
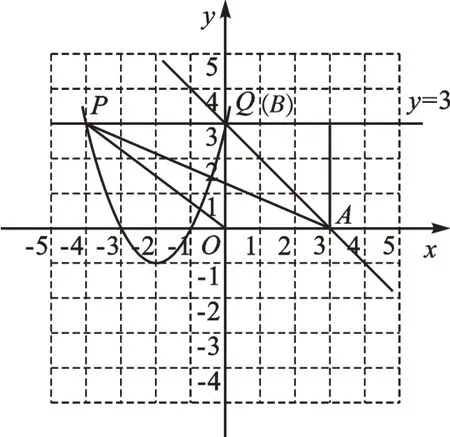
圖7
變式3如圖8,已知關于x的二次函數y1=-x2-2x+n、y2=a(x-3)2-n+1(a>0)滿足對于任意的實數x,都有y1≤1+2n≤y2成立。直線y=kx-k+1(k>0)與函數y1的圖像交于A、B兩點,與函數y2的圖像交于C、D兩點。若對于任意的k>0,都有AB≤CD,結合函數圖像,直接寫出a的取值范圍。

圖8
[設計意圖]學生可以求出n的值為-1,知道直線y=kx-k+1(k>0)經過定點(1,1)。解決本題的關鍵是教師要啟發學生發現兩條拋物線的頂點關于點M(1,1)中心對稱,引導學生結合圖像觀察,最終求出a的取值范圍。
4.回顧小結
小結問題1:本節課繼續研究的是二次項系數為1的二次函數(比如y=x2),你對這類函數的圖像特征有哪些新的認識?
小結問題2:本節課的變式問題與開課時回顧的二次函數(比如y=x2)的圖像特征有什么緊密的聯系?可舉例交流。
[設計意圖]通過課后的小結問題,教師帶領學生課后回顧和反思,一方面回顧本節課所學,另一方面積累本節課教學中的解題經驗和策略。
二、教學反思
1.聚焦核心知識,精心選取習題
在一些重要的章節學習之后,教師會安排幾個課時的習題課教學,這對于鞏固新知是非常必要的。教師如果隨意選取習題,缺少明確的主線或主題,則難以取得良好的教學效果,往往會出現“練過、講過,學生還是出錯”的情形。筆者認為,安排習題課首先要明確教學目標,找出教學主線,圍繞教學主線精選習題。這樣一節課下來,學生對這一類問題及變式題就能有著較為全面的理解,學習效果也能顯著提升。
2.習題課要加強前后教學環節的關聯
為了防止習題課走偏成“題海戰術課”,筆者將本節課習題進行大致歸類,設計成3~4個題組,每個題組是一個教學活動(或教學環節),按由易到難的順序展開教學。每個教學環節最好有明顯的關聯或遞進關系。例如,“基礎熱身”主要是帶領學生復習二次項系數為1的二次函數的圖像特征,而后續的“拾級而上”“拓展提升”這兩個教學環節分別與第一個教學環節關聯和呼應。當學生面對這些變式問題沒有思路時,可以“退回”到第一個教學環節中,重新獲得一些思路和啟示后再挑戰難題,這也是一種“以退為進”的解題策略。
3.精心預設小結問題,引導學生回顧反思
筆者發現,很多習題課教學的最后都沒有課堂小結的時間。著名數學教育家波利亞說過:“習題課教學環節能促進學生對本節課所學的主題、經典圖形、重要性質有一個重新審視、積累經驗的作用。”如本文中的小結問題一樣,教師可以圍繞本節課所學,預設幾個有針對性的小結問題,然后讓學生在這些小結問題的引領之下學會回顧反思,促進經驗分享和知識積累;還可以讓學生課后繼續圍繞本節課訓練的主線,把曾經練習過的同類習題收集、整理在一起,讓學生以解題隨筆或數學寫作的方式梳理成文,在潛移默化中提升解題能力。

