顫振環境軟金屬碰撞滑動接觸摩擦的分子動力學模擬
強寶寶,佟瑞庭,葉軍,權澤芬,王靜巖,李士林
(1.西北工業大學 機電學院,陜西 西安 710072;2.上海飛機設計研究院,上海 200436)
空間高真空、微重力是影響航天器運動機構摩擦和潤滑性能的重要因素[1-3]。日本地球資源衛星一號(JERS-1)因空間環境微重力引發的空間顫振現象,雷達天線展開機構發生冷焊,導致衛星進入預定軌道后雷達天線無法正常展開[4]。美國伽利略號航天器因空間顫振現象引發高增益天線的定位銷與V型槽銷孔之間發生冷焊,造成高增益天線無法展開,導致航天器部分探測任務未完成[5]。國際空間站及哈勃望遠鏡等航天器的運動部件由于空間顫振環境的影響,反復發生摩擦潤滑失效故障[4]。因此,空間摩擦學的研究得到越來越廣泛的關注[6]。
空間環境中,傳統的油、脂潤滑劑易揮發、易爬移,導致機構潤滑不足,而固體潤滑劑因具有低蒸發率、低摩擦阻力等優異性能而得到廣泛應用[7-10]。Ag、Au、Cu等軟金屬,由于低剪切強度,而且具有一定的抗壓強度和韌性,作為固體潤滑劑,能發揮其良好的減摩和潤滑性能[11]。軟金屬固體潤滑劑一般可通過離子鍍、電鍍、磁控濺射等方式附著于基材摩擦副表面,形成軟金屬涂層,實現減摩和潤滑的作用[12]。Tong等[13]通過分子動力學模擬研究了高真空和微重力環境銀薄膜的摩擦性能,結果表明空間顫振會導致銀薄膜的摩擦力顯著增加。袁志威等[14]通過磁控濺射技術在鈦合金表面制備TaC和TaC-Ag涂層與氧化鋁球進行對磨,結果表明,不同溫度下TaC-Ag涂層的磨損率均低于TaC涂層,即加入Ag可提高涂層的耐磨性,因為Ag的添加使TaC晶粒細化,涂層的抗變形性能得以改善。吳耀佳等[15]研究表明,適量的軟金屬Ag與硬質涂層組合,可改善涂層的摩擦性能,提高硬質涂層的耐磨性能;但是添加過多的Ag會降低硬質涂層的耐腐蝕性。尹念等[12]模擬超高真空環境,研究了Au薄膜的摩擦性能,研究結果表明滑動速度較小時,界面之間有大量原子滲透,金屬鍵持續斷裂,摩擦力增大,同時磨損加劇。Tong等[16]通過分子動力學方法模擬真空微重力環境下的碰撞滑動接觸摩擦行為,研究不同壓頭振幅、頻率等對Au薄膜摩擦性能的影響,結果表明,當壓頭振動頻率小于基體固有頻率,壓頭頻率的變化對平均摩擦力影響很小;當壓頭振動頻率大于基體固有頻率,提高壓頭的振動頻率可以減小摩擦力。在固有頻率下,壓頭振幅的變化對平均摩擦力和表面溫度影響不大,在其他頻率下,壓頭振幅對平均摩擦力和表面溫度有明顯影響。Lin等[17]通過模擬研究了Cu薄膜的摩擦性能,結果表明滑動速度較小時,隨著滑動速度增大,摩擦力增大;當滑動速度較大時,Cu薄膜表面溫度升高,表層軟化,摩擦力減小。姚小飛等[18]在TC4鈦合金表面通過硫酸鹽鍍銅技術制備Cu涂層,研究了Cu涂層對TC4鈦合金基材摩擦磨損性能的影響。結果表明,覆有Cu涂層的TC4鈦合金耐磨性優于無涂層的TC4鈦合金基材;無涂層的TC4鈦合金基材主要發生剝層磨損和黏著磨損,覆有Cu涂層的TC4鈦合金會發生剝層磨損和疲勞磨損。Chen等[19]研究表明,與粗粒Cu相比,梯度納米Cu涂層的磨損損失非常低,梯度納米顆粒提高了涂層結構的穩定性,防止在高負荷下晶粒粗化,顯著提高了Cu涂層的耐磨性。以上研究表明軟金屬具有一定的減摩和耐磨作用,但針對真空微重力環境導致的顫振現象對軟金屬摩擦性能的影響仍需進一步研究。
本文采用LAMMPS軟件模擬研究真空微重力環境下軟金屬的摩擦性能。LAMMPS軟件的模擬環境為真空環境,將微重力環境引起空間鉸鏈機構的顫振簡化為圓柱壓頭與基體之間的碰撞滑動接觸運動,建立相應的分子動力學模型。針對空間鉸鏈機構的運動特性,研究不同滑動速度、碰撞速度、壓頭半徑對碰撞滑動接觸摩擦性能的影響,并對比研究Ag、Au與Cu等不同軟金屬的摩擦性能。
1 模型建立
目前含間隙鉸鏈機構在航天器上的應用非常廣泛,如衛星天線展開機構(如圖1所示)、太陽帆板驅動機構、機械臂、紅外地平儀等姿態控制系統中的軸承組件[4],因此以含間隙鉸鏈機構作為空間顫振環境碰撞滑動接觸問題的研究對象。該機構可簡化為由軸和軸承組成,將該模型沿軸向剖開,軸承簡化為上、下基體,軸簡化為圓柱壓頭,如圖2所示。在微重力環境下,摩擦副受到輕微擾動時,會導致軸在軸承內發生無規則碰撞運動,引發顫振。將軸與軸承間的顫振等效為圓柱壓頭沿-z方向的碰撞,將軸的旋轉運動等效為壓頭沿基體表面的水平滑動。因此,在空間微重力環境下,軸與軸承間的運動可等效為圓柱壓頭與基體間的滑動過程和碰撞過程的耦合運動,圓柱壓頭的滑動速度為V1,初始碰撞速度為V0,采用粗粒化分子動力學(CGMD)方法[20]研究碰撞滑動接觸問題。
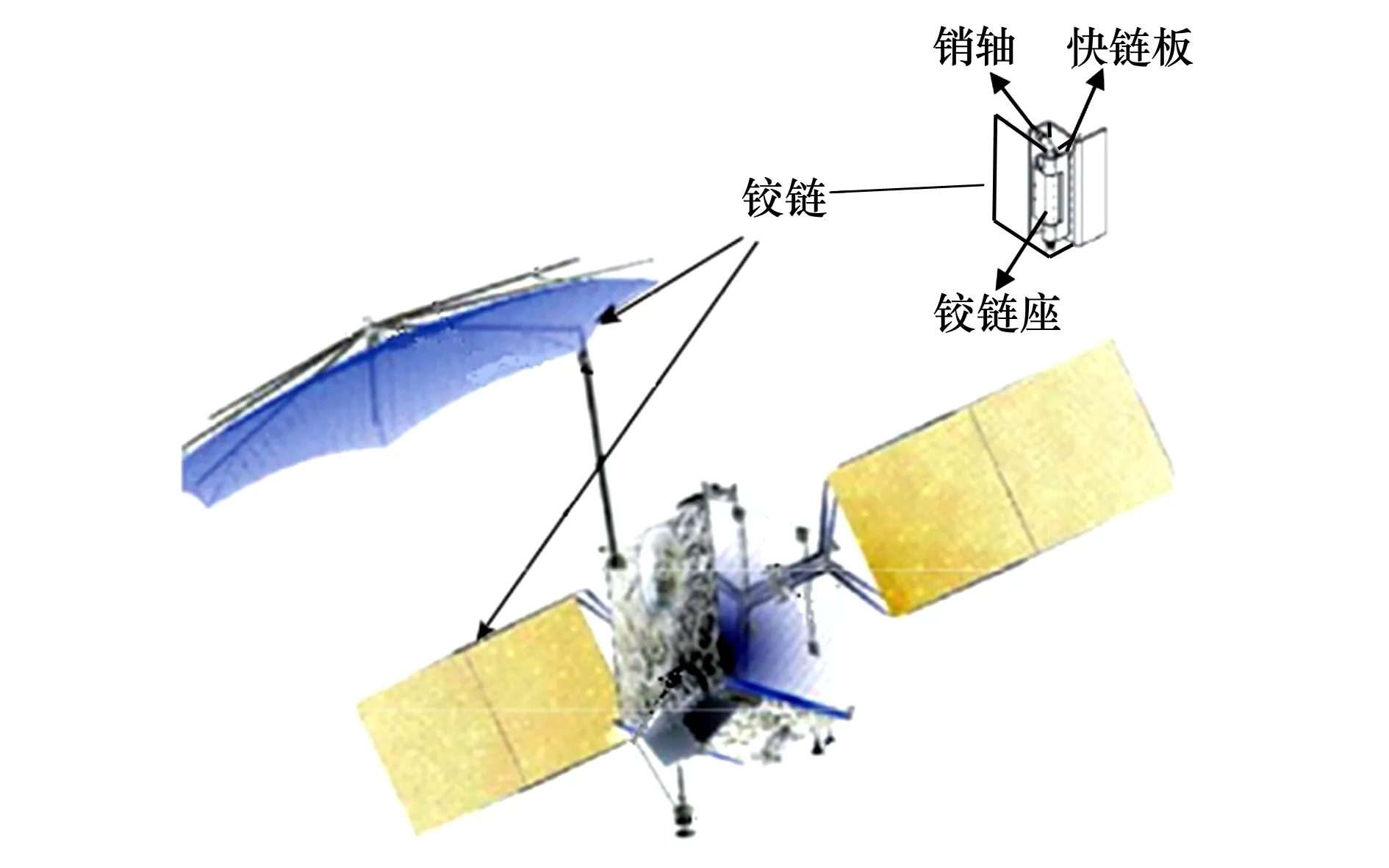
圖1 衛星天線展開機構含間隙鉸鏈圖[4]
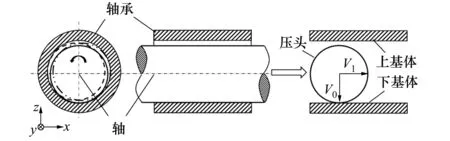
圖2 含間隙鉸鏈機構模型簡化
以軟金屬Au為例,建立碰撞滑動接觸問題的分子動力學模型。基體材料為單晶金,壓頭材料為單晶鐵。模型在x,y,z方向的尺寸分別為114q,20q,100q(q為Au的晶格常數,q=0.408 nm),壓頭半徑為35a(a為Fe的晶格常數,a=0.286 3 nm),上、下基體的尺寸均為114q×20q×18q。為節省模擬計算成本,將壓頭分為3個區域,區域1采用全原子(MD)形式,區域2采用CGMD1,區域3采用CGMD2(CGMD為粗粒化原子模型,CGMD1每個晶格由8個MD晶格組成,其晶格常數等于MD晶格常數的2倍,質量為MD粒子質量的8倍;CGMD2每個晶格由64個MD晶格組成,其晶格常數等于MD晶格常數的4倍,質量為MD粒子質量的64倍)。壓頭上、下各有9層晶格原子為MD形式,與之相鄰的6層晶格原子為CGMD1形式,壓頭中間其余原子為CGMD2形式。基體由邊界層原子、恒溫層原子和牛頓層原子組成。以下基體為例,基體底部的3層原子為邊界層,與邊界層相鄰的3層原子為恒溫層,基體其余原子為牛頓層原子。基體的x方向和y方向采用周期性邊界條件以減少尺寸效應的影響,在z方向采用固定邊界條件。分子動力學模型如圖3所示。
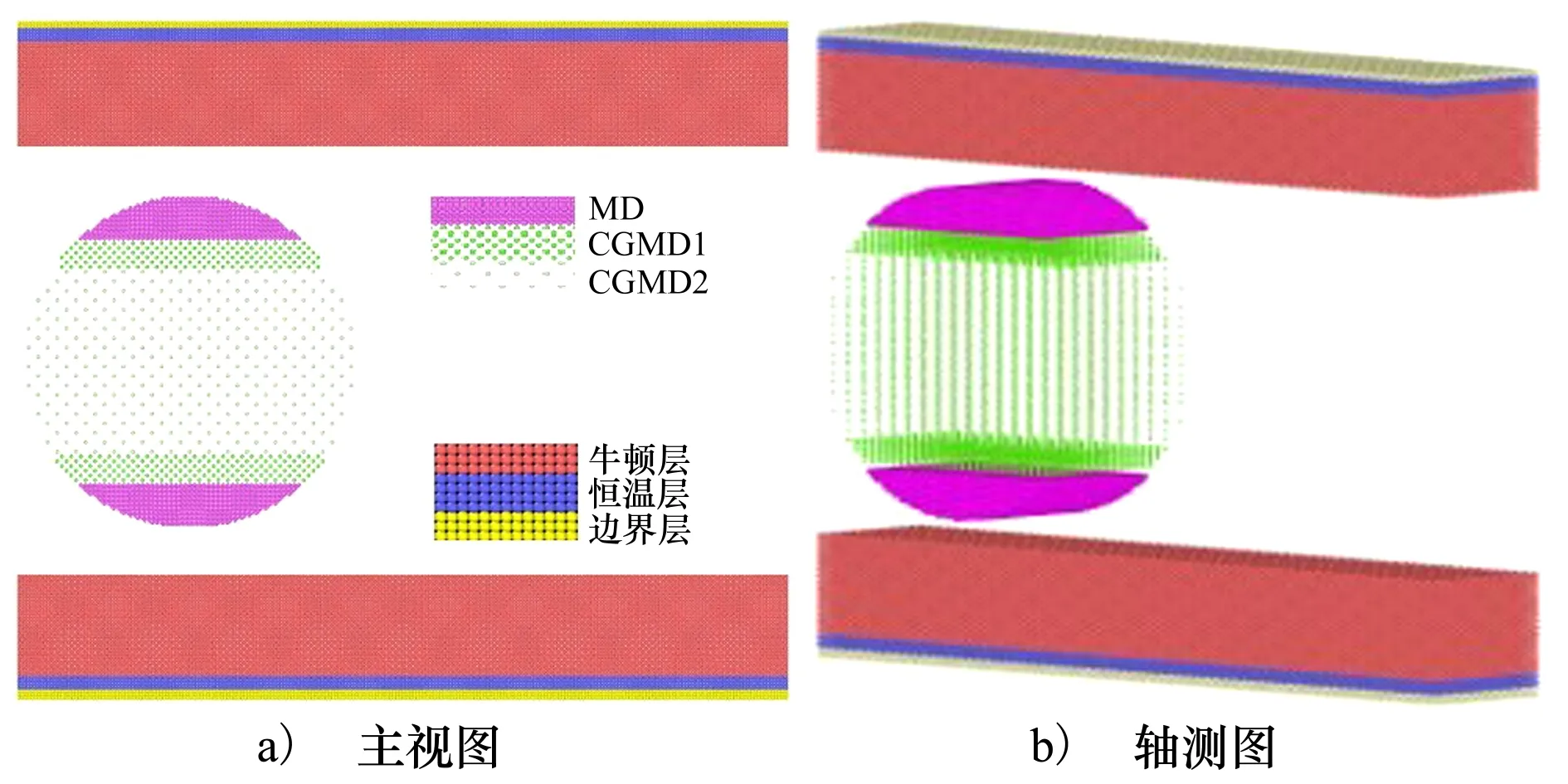
圖3 碰撞滑動接觸粗粒化分子動力學模型
模擬過程中,基體恒溫層和牛頓層原子的運動遵循牛頓第二定律,以velocity-Verlet算法求解運動方程,設置時間步長為0.01 ps。壓頭發生運動前,采用NVT系綜對系統進行弛豫,恒溫層原子和牛頓層原子的弛豫溫度為300 K,弛豫時間為50 ps,之后將系統轉入NVE系綜,弛豫50 ps至系統達到平衡。弛豫完成后,壓頭以碰撞速度V0(-z方向)、滑動速度V1(x方向)開始運動。
采用EAM勢函數描述基體金屬原子間的相互作用,采用Morse勢函數描述Fe壓頭與基體金屬原子間的相互作用。將壓頭等效為剛體,忽略壓頭內部原子間的相互作用。
關于EAM勢,金屬基體原子的總能量EM由(1)式計算
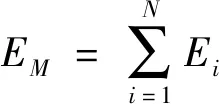
(1)
式中,原子i的能量Ei由(2)式計算

(2)
式中:Fi是原子i的嵌入能;ρi是由基體中所有其他原子產生的位于位置i的電子密度;φij是原子i和j之間的對勢。
Morse勢由(3)式計算
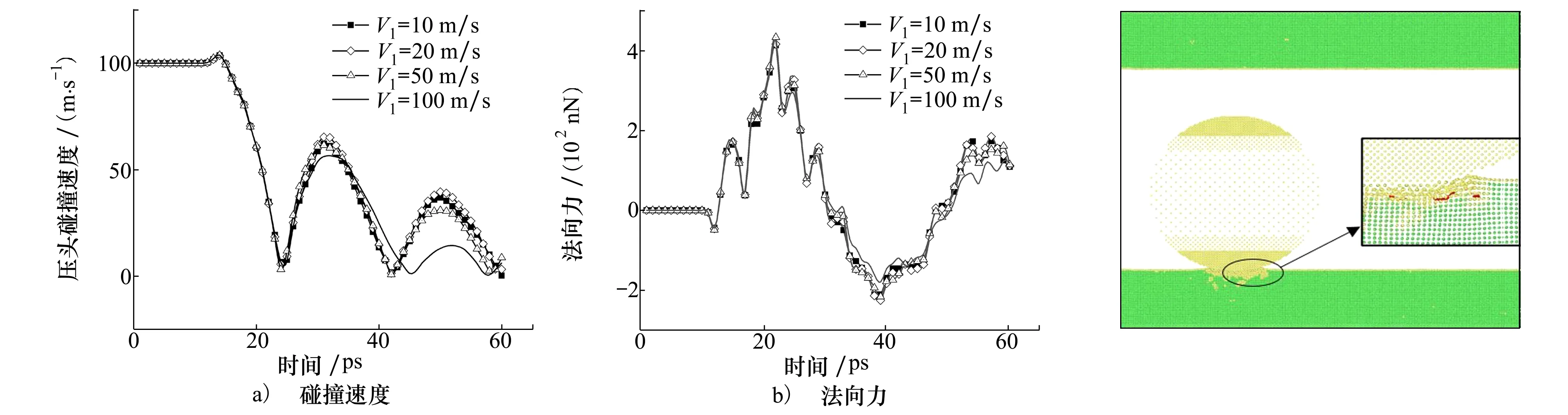
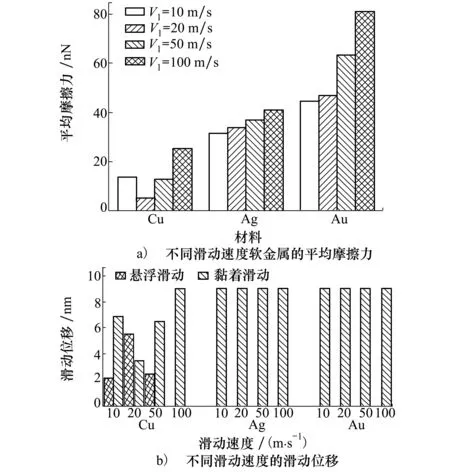
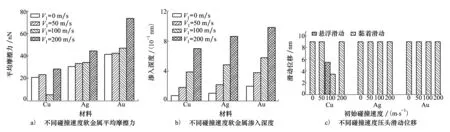
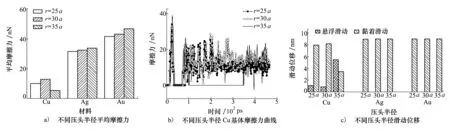
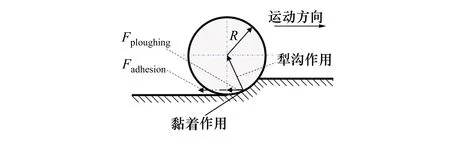
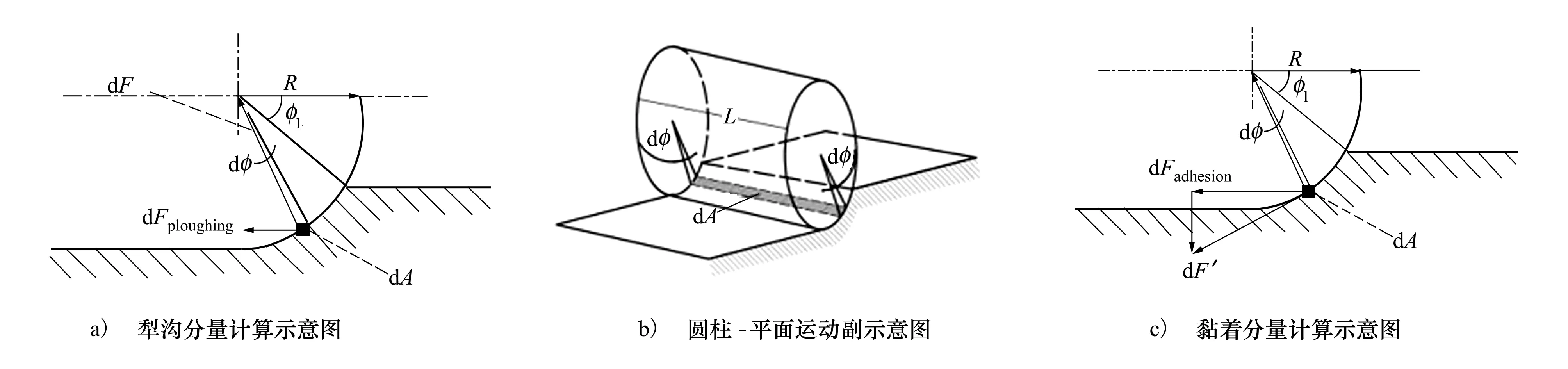
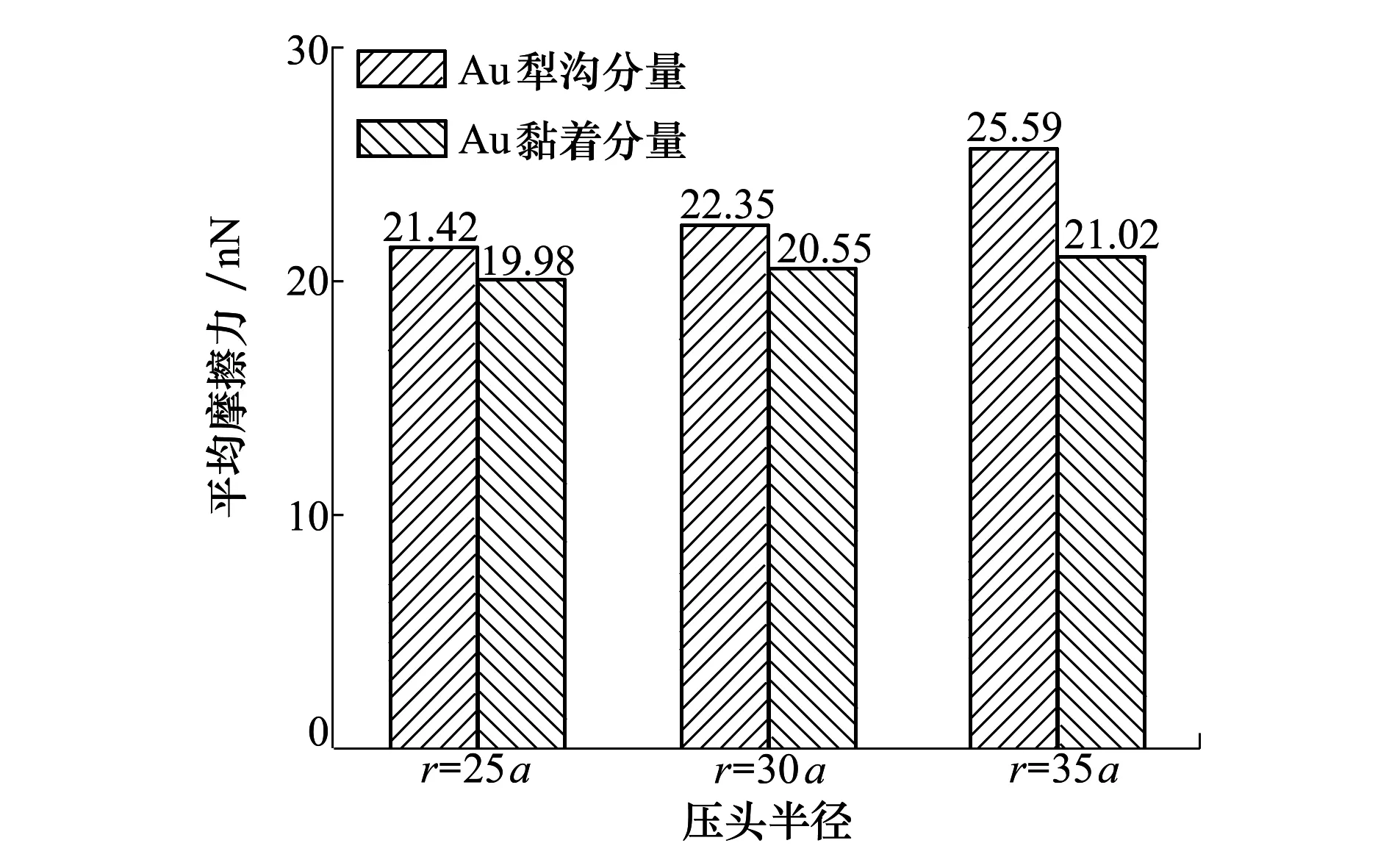
E=D0[e-2a(r-r0)-2e-a(r-r0)]r (3) 式中:D0是結合能;α是材料參數;r0是平衡距離;rc是截斷半徑;r是原子間距離。 根據Morse勢混合規則[21],得到Fe-Cu、Fe-Ag、Fe-Au的勢參數[22-23],如表1所示。 表1 Morse勢參數 在顫振環境下,研究壓頭與基體之間不同滑動速度對摩擦性能的影響。壓頭在-z方向的初始碰撞速度為100 m/s,在x方向的滑動速度分別為10,20,50和100 m/s,滑動位移為9 nm。 基體材料為Au時,取前60 ps的壓頭碰撞速度曲線,分析壓頭與基體間的碰撞過程,如圖4a)所示,與之相對應的法向力曲線如圖4b)所示。圖5是滑動速度為20 m/s、時間t=17 ps時基體的位錯圖。 如圖4所示,壓頭的碰撞速度曲線以及法向力曲線在不同滑動速度下均呈現出類似的波動趨勢,取滑動速度為20 m/s進行分析。壓頭與基體的碰撞過程分為3個階段:碰撞階段、回彈階段和黏著分離階段。在碰撞階段中,如圖4a)所示,t=13 ps時,壓頭碰撞速度V0=103.8 m/s,略大于壓頭的初始碰撞速度100 m/s。當壓頭與基體即將接觸時,由于分子間相互作用力以吸引力為主(如圖4b)所示,t=10~12 ps時壓頭與基體之間的相互作用力為負值,表現為相互吸引力),該吸引作用力與壓頭運動方向相同,對壓頭產生一定的加速作用,因此,壓頭碰撞速度呈現出微小增大。壓頭與基體接觸之后,法向力逐漸增大,此時法向力阻礙壓頭向下運動,壓頭的碰撞速度逐漸減小。圖4b)中,t=17 ps時法向力突然減小,之后繼續增大,這是因為t=17 ps時,在壓頭作用下基體開始出現了位錯(如圖5所示,滑動速度為20 m/s、時間t=17 ps時基體發生了位錯,紅色線為基體位錯線,綠色原子為FCC結構,黃色原子為其他結構),位錯的產生使基體上累積的部分應變能得以釋放,因此法向力會瞬時減小,而隨著壓頭繼續下壓,法向力會逐漸增大。當碰撞速度減小至零時,壓頭處于基體的最大滲入深度處,此時法向力達到最大值,對應于圖4b)中t=22 ps時刻,法向力達到最大為417.11 nN。此后,壓頭進入回彈階段,壓頭開始向上運動,此時法向力作為壓頭回彈的動力,壓頭速度逐漸增大,法向力逐漸減小。當法向力趨于零時,壓頭達到回彈的最大速度(如圖4a)~4b)中,t=31 ps時,法向力為零,壓頭達到回彈最大速度),此后壓頭進入黏著分離階段。壓頭繼續向上運動,由于黏著作用,壓頭與基體之間的作用力阻礙壓頭向上運動,因此壓頭的速度逐漸減小。由于壓頭與Au基體黏著作用較大,無法碰撞分離,此后壓頭會在z方向產生微小幅度振蕩,并沿x方向繼續勻速滑動。 此外,如圖4a)所示,壓頭水平滑動速度分別為10,20,50和100 m/s,由于壓頭與Au基體的黏著作用較大,無法碰撞分離,壓頭在z方向振蕩,壓頭的動能補償振蕩過程中黏著作用消耗的能量,因此碰撞速度會逐漸減小。隨著滑動速度的增大,壓頭在z方向的碰撞速度衰減加快。滑動接觸過程以黏性阻尼為主,滑動速度越大,壓頭在碰撞滑動過程中能量損耗越大,碰撞速度衰減越快。 圖4 不同滑動速度壓頭的碰撞速度、法向力曲線圖5 滑動速度為20 m/s、時間t=17 ps時基體位錯圖 不同滑動速度下,Au、Ag、Cu軟金屬的平均摩擦力、滑動位移如圖6所示。圖6a)中,隨著滑動速度增加,壓頭與Cu基體的平均摩擦力先減小后增大,壓頭與Ag基體和Au基體的平均摩擦力逐漸增大。當滑動速度較小時,壓頭與Cu基體可碰撞分離,且懸浮滑動位移(懸浮滑動是指壓頭與基體碰撞分離后,壓頭會沿x方向繼續滑動,此時壓頭處于懸浮狀態)隨滑動速度的增加先增大后減小(如圖6b)所示,滑動速度為10,20和50 m/s時,懸浮滑動位移分別為2.1,5.52和2.45 nm)。由于懸浮滑動過程中,壓頭與基體間作用力較小,因此摩擦力呈現出先減小后增大趨勢。當滑動速度較大時,壓頭與Cu基體始終處于黏著滑動接觸狀態,基體對壓頭黏著作用增強,因此摩擦力較大。壓頭與Ag基體和Au基體無法碰撞分離,始終處于黏著滑動狀態,且隨著滑動速度增大,黏著作用增強,摩擦力增大。 圖6 不同滑動速度軟金屬的平均摩擦力、滑動位移 顫振環境下,不同碰撞速度會對壓頭與基體間的相互作用產生重要影響。選取-z方向的初始碰撞速度分別為0,50,100與200 m/s,壓頭在x方向的滑動速度為20 m/s,滑動位移為9 nm,研究碰撞速度對摩擦性能的影響。壓頭初始碰撞速度為0 m/s,即壓頭與基體不發生碰撞,系統弛豫完成后,壓頭在-z方向以10 m/s的速度靠近基體,以壓頭與基體之間即將產生相互作用力為臨界點,認為壓頭與基體恰好接觸,將壓頭的速度和作用力清零,再次對系統進行弛豫至平衡。然后壓頭以20 m/s的速度沿x方向滑動,模擬無碰撞滑動接觸摩擦過程。 不同碰撞速度下,Au、Ag、Cu軟金屬的平均摩擦力、滲入深度和滑動位移如圖7所示。圖7a)中,隨著碰撞速度的增大,壓頭與Cu基體間的平均摩擦力先增大后減小再增大,壓頭與Ag基體和Au基體間的摩擦力逐漸增大。當碰撞速度較小時,壓頭動能較小,與基體碰撞會導致部分能量損失,壓頭回彈的動能較小,無法克服Cu基體對壓頭的黏著作用,壓頭無法從基體碰撞分離,與Cu基體始終處于黏著滑動狀態(如圖7c)所示)。壓頭與基體不發生碰撞分離的情況下,碰撞速度越大,黏著作用越強,摩擦力越大,如圖7a)中碰撞速度小于100 m/s的情況。隨著碰撞速度繼續增加,壓頭動能增大,壓頭回彈的動能較大,對于Cu基體,壓頭可碰撞分離,壓頭與基體之間的部分滑動處于懸浮滑動狀態,黏著滑動位移較小(圖7c)中碰撞速度為100 m/s時,壓頭與Cu基體懸浮滑動位移為5.52 nm,黏著滑動位移為3.48 nm),因此摩擦力較小。當碰撞速度更大(如碰撞速度為200 m/s)時,基體的滲入深度增大,接觸面積增加,黏著作用增強,壓頭與Cu基體無法碰撞分離,始終處于黏著滑動狀態,因此摩擦力較大;如圖7b)中碰撞速度為200 m/s時,基體的滲入深度顯著增加,且壓頭與Cu基體始終處于黏著滑動狀態(如圖7c)所示),導致摩擦力較大。壓頭與Ag基體和Au基體始終處于黏著滑動狀態(如圖7c)所示),初始碰撞速度越大,壓頭動能越大,基體滲入深度越深,接觸面積越大,黏著作用越強,摩擦力也越大。 圖7 不同碰撞速度軟金屬的平均摩擦力、滲入深度和滑動位移 壓頭半徑對基體與壓頭的接觸面積有重要影響,選取壓頭半徑分別為25a,30a,35a,壓頭在x方向的滑動速度為20 m/s,在-z方向的初始碰撞速度為100 m/s,滑動位移為9 nm,研究壓頭半徑對軟金屬摩擦性能的影響。 不同壓頭半徑的平均摩擦力、Cu基體摩擦力曲線、滑動位移如圖8所示。圖8a)中,隨著壓頭半徑增大,壓頭與Cu基體間的平均摩擦力先增大后減小,壓頭與Ag基體和Au基體間的平均摩擦力逐漸增大。當壓頭半徑分別為25a與30a時,壓頭與下基體Cu均可碰撞分離1次,最終與上基體Cu發生黏著滑動,且壓頭半徑越大,動能越大,與下基體碰撞分離后回彈速度越大,懸浮滑動位移越小,黏著滑動位移越大(如圖8c)所示),導致摩擦力越大。當壓頭半徑為35a時,壓頭與Cu基體可碰撞分離2次,最終在下基體Cu上持續黏著滑動,壓頭懸浮滑動位移較長,黏著滑動位移較短,因此平均摩擦力較小。由于壓頭與Ag基體和Au基體未發生碰撞分離,始終處于黏著滑動狀態(如圖8c)所示),隨著壓頭半徑增大,動能增大,壓頭與基體的接觸面積增加,摩擦力增大。 圖8 不同壓頭半徑的平均摩擦力、Cu基體摩擦力曲線和滑動位移 圖8b)為不同半徑壓頭與Cu基體之間的摩擦力曲線,t=31~84 ps時,壓頭與基體之間摩擦力為零,且半徑越大,維持的時間越短。由于壓頭與Cu基體可碰撞分離,碰離后壓頭與基體處于懸浮滑動狀態,因此摩擦力為零,且壓頭半徑越大,動能越大,碰離后速度越大,z方向間隙相同時,所需時間越短。半徑分別為25a與30a時,半徑越大,摩擦力越大。因為半徑越大,動能越大,壓頭與下基體碰離后的速度越大,與上基體的碰撞速度就越大,滲入深度越深,壓頭與上基體的接觸面積越大,因此摩擦力越大。半徑為35a時,壓頭與上、下基體均可碰撞分離,與上基體碰離后壓頭的速度較小,懸浮滑動時間較長(t=102~345 ps時,壓頭與基體處于懸浮滑動狀態),黏著滑動位移較短,因此摩擦力較小。 此外,針對圖8a)中不同壓頭半徑時Au基體的平均摩擦力進行詳細的理論分析探討。根據經典摩擦學理論[24-25],摩擦力主要由兩部分組成,一部分是由于摩擦副的界面剪切黏著作用形成的黏著分量,另一部分是由于材料變形阻礙壓頭向前運動的犁溝作用形成的犁溝分量,如圖9所示,總摩擦力可以表示為 F=Fploughing+Fadhesion (4) 式中:Fploughing為犁溝分量;Fadhesion為黏著分量。 圖9 圓柱-平面運動副摩擦力組成示意圖 由圖9可知,犁溝作用是基體沿垂直于接觸面的方向對壓頭的作用力,摩擦力的犁溝分量為犁溝作用沿運動方向的分量。根據圖10a)~10b)推導圓柱形壓頭與基體摩擦過程中摩擦力的犁溝分量,假設金屬的屈服極限是各向同性的,則接觸面積dA為 dA=RLdφ (5) 式中:R為圓柱形壓頭半徑;L為圓柱形壓頭長度。 圖10 圓柱-平面運動副摩擦力計算示意圖 圓柱形壓頭的犁溝作用dF為 dF=δsdA (6) 式中,δs為金屬屈服極限。 dF沿運動方向的分量為 dFploughing=dFcosφ=δsRLcosφdφ (7) 對dFploughing從φ1到π/2積分即可求得犁溝分量 Fploughing= (8) 如圖10c)所示,圓柱形壓頭與基體間的黏著作用為 dF′=δcdA (9) 式中,δc為剪切強度。 dF′沿運動方向的分量為 dFadhesion=dF′sinφ=δcRLsinφdφ (10) 對dFadhesion從φ1到π/2積分即可求得黏著分量為 (11) 根據摩擦力的犁溝分量和黏著分量可知,當增大圓柱形壓頭半徑時,摩擦力的犁溝分量和黏著分量都會增加。如圖8a)中Au基體的平均摩擦力用摩擦分量表示如圖11所示。隨著壓頭半徑增大,犁溝分量和黏著分量增大。由于壓頭半徑增大時,動能增加,壓頭與基體的滲入深度增大,阻礙壓頭向前運動的犁溝作用增強,導致摩擦力的犁溝分量增大;同時壓頭與基體的接觸面積增加,摩擦副剪切黏著作用增強,導致摩擦力的黏著分量增大。 圖11 不同壓頭半徑Au基體的摩擦分量 1) 當滑動速度較小時,壓頭與Cu基體發生碰撞分離,且懸浮滑動位移隨滑動速度的增加表現為先增大后減小,因此摩擦力先減小后增大。當滑動速度較大時,壓頭與Cu基體始終處于黏著滑動狀態,摩擦力較大。壓頭與Ag基體和Au基體始終處于黏著滑動狀態,隨著滑動速度增加,摩擦力增大。 2) 當碰撞速度較小時,壓頭與Cu基體始終處于黏著滑動狀態,且碰撞速度越大,黏著作用越強,摩擦力越大。當碰撞速度增大時,壓頭與Cu基體之間的部分滑動處于懸浮滑動狀態,摩擦力較小。繼續增大碰撞速度,壓頭與Cu基體始終處于黏著滑動狀態,壓頭在基體的滲入深度較大,接觸面積增加,黏著作用增強,摩擦力較大。壓頭與Ag基體和Au基體始終處于黏著滑動狀態,初始碰撞速度越高,壓頭動能越大。壓頭動能的增大導致基體滲入深度增大,進一步使接觸面積增加,從而導致摩擦力增大。 3) 壓頭半徑分別為25a,30a和35a時,壓頭在Cu基體均發生碰撞分離,壓頭與基體之間的部分滑動處于懸浮滑動狀態,且半徑為35a時,壓頭與Cu基體碰撞分離2次,懸浮滑動位移較長,黏著滑動位移較短,摩擦力較小。壓頭與Ag基體和Au基體始終處于黏著滑動狀態,隨著壓頭半徑增大,動能增加,壓頭與基體的滲入深度增大,阻礙壓頭向前運動的犁溝作用增強,導致摩擦力的犁溝分量增大;同時壓頭與基體的接觸面積增加,摩擦副剪切黏著作用增強,導致摩擦力的黏著分量增大。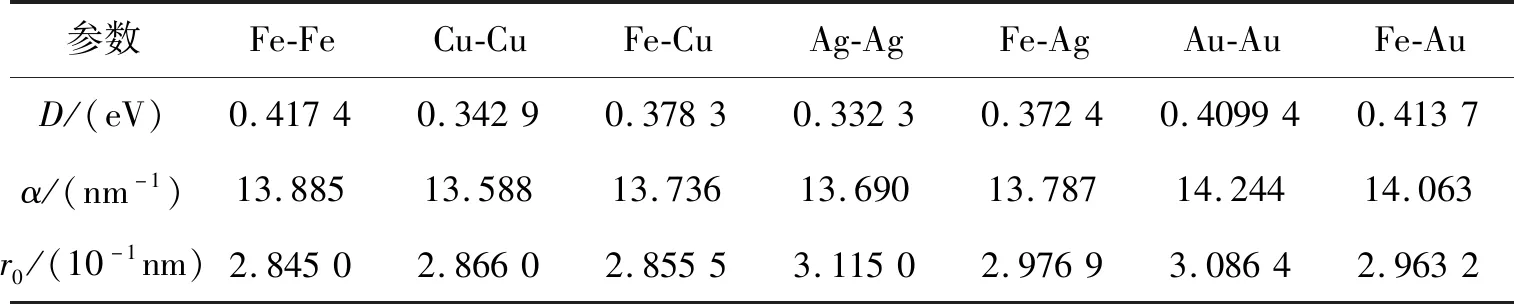
2 結果與分析
2.1 滑動速度的影響
2.2 碰撞速度的影響
2.3 壓頭半徑的影響
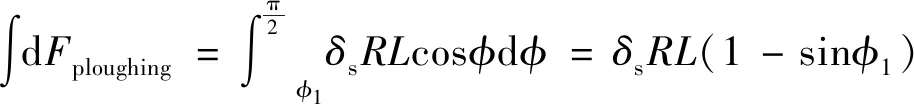
3 結 論

