基于復數陷波器的改進雙二階廣義積分鎖相環

王 濤，陳 榮

（1.江蘇大學電氣信息工程學院，江蘇鎮江 212013；2.鹽城工學院電氣信息工程學院，江蘇鹽城 224051）

隨著化石能源的不斷減少和環境的日益惡化，可再生能源得到大規模發展，利用風能、太陽能等可再生能源進行發電，是應對能源不斷減少和環境不斷惡化等問題的重要措施。在新能源并網發電系統中，需要實時獲取電網同步信息以確保并網逆變器可靠、穩定、同步運行。鎖相技術是確保并網系統穩定運行的關鍵技術之一，其性能的好壞直接決定逆變器向電網輸送電能的質量[1]。鎖相環是獲取輸入信號相位信息的常用方法，在通信系統中的信號調制與解調[2]、電機控制系統中的電機轉速與位置信息[3]、并網發電系統的電網同步信息[4]等領域中，鎖相環應用十分廣泛。

對于理想電網電壓而言，傳統單同步旋轉坐標系鎖相環(Synchronous Reference Frame-Phase Locked Loop，SRF-PLL)可以快速準確地獲取相位信息，然而在實際系統中，電網電壓不平衡、含有直流及諧波分量時有發生，SRF-PLL 已不能滿足準確提取相位的要求。文獻[5-6]采用高通濾波器對輸入信號中的直流分量進行消除，由于是直接對輸入信號進行濾波處理，濾波后的信號在基頻處會產生幅值和相位誤差，因此需設計補償環節進行校正。文獻[7]提出一種正交消諧法消除諧波分量，以實現準確鎖相，但涉及到微分運算，易放大噪聲信號。文獻[8]提出在兩相靜止坐標系下級聯二階陷波器消除諧波，但運算量相對較大，且每相都需要一個二階陷波器。

為此，文中提出一種改進型雙二階廣義積分鎖相環，在誤差通道中級聯復數陷波器對直流和諧波進行消除，不需要設計補償環節進行校正，并且所需的復數陷波器相比傳統二階陷波器始終少一個。

1 正負序提取及二階廣義積分器

1.1 正負序分量提取

當三相電網不平衡時，常利用對稱分量法分解為正序分量和負序分量，可表示為：

式（1）中，[C32]和[C32]-1分別為Clarke 變換及其逆變換的變換矩陣，[Tabc]+和[Tabc]-分別為三相坐標系下的正、負序變換矩陣，q=-j，是一個滯后90°的移相旋轉因子。

由式（1）可知，若要獲得正負序分量，就需要獲得vα和vβ以及它們滯后90°的正交信號qvα和qvβ。

1.2 二階廣義積分器

由內模原理可知，跟蹤某一特定頻率的信號時,要求開環傳遞函數中含有該信號的s域模型。正弦信號的拉普拉斯變換為二階廣義積分，使用二階廣義積分器可跟蹤輸入信號，同時利用積分器產生滯后90°的正交信號[9]。基于二階廣義積分的正交信號發生器(Quadrature Signal Generator based on Second-Order Generalized Integrator，SOGI-QSG)結構圖如圖1所示。

圖1 SOGI-QSG結構圖

根據圖1 可以得到SOGI 和輸出兩正交信號與輸入信號之間的傳遞函數，其表達式為：

傳遞函數D(s)和Q(s)的伯德圖如圖2 所示。

圖2 D(s)、Q(s)傳遞函數的伯德圖

由圖2 可以看出，D(s)為二階帶通濾波器，Q(s)為二階低通濾波器。在中心頻率ω′處，幅值增益為1，相位分別為0°和-90°。由式（2）可知，濾波器的帶寬僅取決于增益系數k，與中心頻率ω′無關，也就是說，僅調節k的值就可以設定其帶寬，從而改變濾波器的動態性能和濾波性能。具體來說，k值越大，帶寬越寬，濾波性能就越弱，動態響應時間就越短；k值越小，結論與之相反。因此，為了兼顧濾波性能和動態性能，k的取值一般在1.414 附近[10]。

2 改進型DSOGI

2.1 直流和諧波分量消除原理

在實際應用中，受A/D 轉換誤差、模擬器件溫度、零點漂移[11-12]以及PCC 處接有非線性負載等因素的影響[13]，輸入電網電壓信號中可能含有直流分量和諧波分量。

假設輸入電壓信號中只含有直流分量干擾，當系統到達穩態時，暫態指數部分衰減為0，輸出信號v′中不含直流分量，而qv′中含有直流分量，此時的輸入輸出信號可以用下式進行表示：

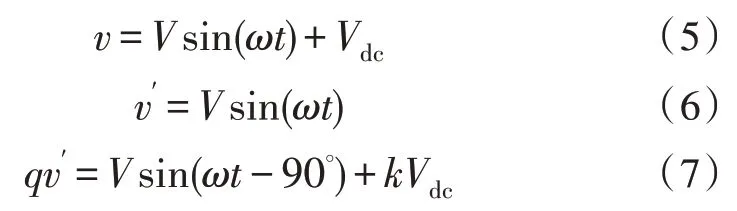
由式（5）-（7）分析可得，將輸入信號v與輸出信號v′反饋作差，則誤差信號εv中僅含有直流分量Vdc，直流分量是一個常數，其導數恒等于0，因此，可以考慮在誤差通道中直接引入一個微分器，相當于給系統增加一個零點，但微分器較難實現，而且微分器的幅值增益隨頻率線性上升，對高頻噪聲信號非常敏感，系統的穩定性將會受到影響。故文中將微分器用高通濾波器(HPF)來代替，高通濾波器的傳遞函數為:

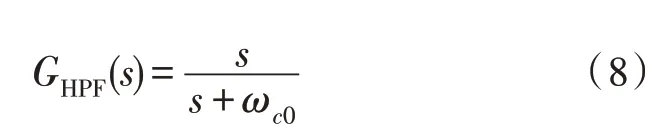
當電網中含有干擾程度較大的低次諧波（如5次和7 次）時，由圖2 伯德圖可知，濾波器對其抑制能力不足，因此，輸出信號中的基波信號不純凈。與直流分量消除原理相同，此時誤差通道中含有諧波分量，基于增加諧波頻率處零點的思想，同理可得，諧波分量使用復頻移的高通濾波器進行消除，即復數陷波器(Complex Notch Filter，CNF)，其表達式為：

式（9）表明，復數陷波器將零點配置在nω處，故可以消除干擾程度較大的特定次諧波。特別地，當n=0 時，復數陷波器變為高通濾波器。實際上，高通濾波器可以看作是消除直流分量（0 Hz）的復數陷波器。

在兩相靜止坐標系下，xα、xβ和yα、yβ分別為兩輸入和輸出，始終保持天然正交，即滿足xα=jxβ且yα=jyβ，因此，依據此性質，可以巧妙地實現復數陷波器。對式（9）進行改寫，整理成狀態空間方程的形式，可得表達式為：

根據式（10）實現復數陷波器，其結構框圖如圖3所示。

圖3 復數陷波器實現結構框圖

2.2 改進DSOGI-PLL整體結構

將復數陷波器和高通濾波器級聯嵌入在誤差通道中，改進型DSOGI(Dual Second Order Generalized Intergrator)結構如圖4 所示。

圖4 改進型DSOGI原理結構框圖

根據圖4，以5 次和7 次諧波為例，結合式（2）-（4）、式（8）和式（9），改進型DSOGI 的傳遞函數D1(s)和Q1(s)分別為：

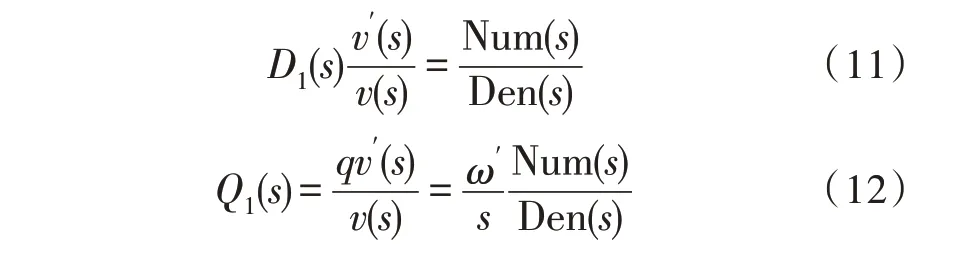
當實際電網頻率ω與濾波器中心頻率ω′相同時，令s=jω，可得：

所以，改進型DSOGI 結構依舊能夠無衰減零相移地從輸入信號中提取出基頻信號和滯后90°的正交信號，且能消除直流和諧波分量的影響，不需要設計復雜的相位和幅值補償；然后通過PNSC 模塊分離正序和負序分量；最后結合SRF-PLL 完成鎖相，得到的改進型DSOGI-PLL 結構整體如圖5 所示。

圖5 改進型DSOGI-PLL結構框圖

2.3 改進DSOGI相關參數選擇

改進DSOGI 的性能品質取決于其結構中的增益系數k與加入的復數陷波器的截止頻率ωcn。為簡化設計，保持增益系數k與傳統一致，即k=1.414，ωcn的選取范圍由式（8）的特征方程決定，可通過勞斯穩定判據判斷求出范圍。由于特征方程為5 階，階數較高，故文中在Simulink 里使用Model Linearizer 線性分析工具來判斷ωcn參數變化對濾波器的影響。分析可得，當ωcn過小時，動態時間會變慢；而當ωcn過大時，會使得正交信號產生振蕩。因此，綜合考慮動態響應速度、濾波強度和穩態特性，折中選取參數，使濾波器獲得較優的性能品質，文中選取k=1.414,ωc0=78.5,ωc5=392.5,ωc7=549.5。

3 仿真分析

為驗證文中所設計的新型鎖相環在電網電壓不平衡、含有直流分量以及含有諧波的情況下的有效性，在Matlab/Simulink 軟件中搭建了仿真模型，同時搭建了DSOGI-PLL 和自調諧PLL[14-15]的仿真模型進行對比驗證。根據對稱最優化設計[16]，鎖相環路中的PI 控制器參數設置為kp=88.8，ki=3 947.8。

3.1 電網電壓不平衡

在0.3 s 時刻，設置輸入電壓不平衡跌落，保持A相電壓正常，設定B 相電壓跌落10%，C 相電壓跌落45%，仿真結果如圖6 所示。

圖6 電網電壓不平衡下仿真波形

圖6（a）為兩相幅值歸一化后的電壓波形，在0.3 s 之前為理想電壓，在0.3 s 之后，電壓設定不平衡跌落；圖6（b）是使用文中方法對輸入信號進行預處理提取正序電壓分量的波形；圖6（c）為文中方法、DSOGI-PLL 和自調諧PLL 三種鎖相頻率圖，這三種方法都可以準確檢測鎖相頻率，但在超調量與穩態調節時間上有所差距。

3.2 含有直流分量

在0.3 s 時刻，設置輸入電壓含有直流分量，A 相加入50 V 的直流分量，B 相加入20 V 的直流分量，C相加入30 V 的直流分量，仿真結果如圖7 所示。

圖7 含直流分量的仿真波形

由圖7（c）可知，由于DSOGI-PLL 和自調諧PLL對直流分量抑制能力不足，因此，基準正序電壓分量里含有直流分量擾動，PLL 頻率出現較大波動；而文中設計的新型鎖相環能夠完全消除直流分量，可以快速準確地檢測鎖相頻率。

3.3 含有諧波分量

在0.3 s 時刻，設置輸入電壓含有諧波分量，在三相電壓中加入0.2 pu 的5 次諧波和0.1 pu 的7 次諧波，仿真結果如圖8 所示。

由圖8（c）可知，DSOGI-PLL 對5 次、7 次諧波抑制能力不足，故基準信號中基頻信號不純凈，鎖相頻率 在-0.5～0.5Hz之間波動；自調諧PLL相對于DSOGI-PLL，在其基礎上增加了類GI 自適應濾波器，諧波抑制能力得到增強，具體可以參考文獻[14]，鎖相頻率僅在-0.2～0.2 Hz 之間波動；而文中方法能夠完全消除諧波分量的影響，大約經過2.5 個工頻周期，鎖相頻率恢復穩定，穩態幾乎無波動。因此，文中所提的新型鎖相環的檢測頻率精度更高，鎖相效果更好。

圖8 含諧波分量的仿真波形

4 結論

文中在傳統DSOGI-PLL 的基礎上，提出了一種可以同時應對電網電壓不平衡、含有直流及諧波條件下的新型鎖相環，該鎖相環能夠滿足電壓頻率和相位等信息的快速準確檢測[17-18]。文中詳細分析了如何消除直流分量和干擾程度較大的諧波分量，在DSOGI 的誤差通道中采用級聯形式的復數陷波器，組成改進型DSOGI 前置濾波器，結合PNSC 模塊提取正序分量，最后通過PLL 獲取頻率和相位等信息。所設計的鎖相環精度高，對新能源發電并網具有一定的應用價值。