Fm、Pn⊙Fm和Cn⊙Fm的r-hued染色研究

西日尼阿依·努爾麥麥提, 劉鳳霞

(1. 喀什大學 數學與統計學院, 新疆 喀什 844000; 2. 新疆大學 數學與系統科學學院, 新疆 烏魯木齊 830046)

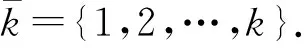
圖的r-hued染色的概念首次由Montgomery等[1]提出,并在文獻[2]中得出了特殊情形r=2的一些結果.在早期階段,2-hued染色被稱為dynamic染色.文獻[3]首次研究了關于r的一般值的r-hued染色,并且r-hued染色被稱為條件染色.在后來的研究中,專業名稱還沒統一,但大多數研究者都在使用“r-hued染色”或者“r-dynamic染色”.

(C1) 若uv∈E(G),則c(u)≠c(v);

(C2) 對于任意v∈V(G),則

|c(NG(v))|≥min{|NG(v)|,r}.

引理 1[3]χ(G)=χ1(G)≤χ2(G)≤…≤χΔ(G)(G)=χΔ(G)+1(G)=…=χ(G2),如果r≥Δ(G),那么χr(G)=χΔ(G)(G).

圖G的平方圖記為G2,表示滿足V(G2)=V(G),uv∈E(G2),當且僅當點u、v在圖G中的距離最多是2的圖.

引理 2[3]設G是一個圖,則有χr(G)≥min{Δ(G),r}+1,其中r≥1.

圖G和圖H的corona乘積圖記為G⊙H,是將圖G拷貝一份、圖H拷貝|V(G)|份,把圖G的第i個頂點跟圖H的第i(1≤i≤|V(G)|)個拷貝份的每個頂點連邊而得到的圖.關于2個圖的corona乘積圖的r-hued染色數的研究早期已有很多結果,比如:在2017年,Kristiana等[5]刻畫了路與路、路與圈、路與輪圖的corona乘積圖的r-hued染色數;在2018年,Kristiana等[6]刻畫了星圖和輪圖、輪圖和輪圖的corona乘積圖的r-hued染色數,Kristiana等[7]刻畫了星圖與完全圖、完全圖與完全圖的corona乘積圖的r-hued染色數等.

本文主要研究Fm、Pn⊙Fm和Cn⊙Fm的r-hued染色數.

1 Fm的r-hued染色數

本節主要研究扇圖Fm的r-hued染色數,先給出本文的結論.

定理 1設Fm是一個扇圖,m≥2,則

證明扇圖Fm是頂點集合為

V(Fm)={u0,u1,u2,…,um},邊集合為

E(Fm)={u0ui|1≤i≤m}∪

{uiui+1|1≤i≤m-1}

的連通圖,其頂點個數為

|V(Fm)|=m+1,邊的個數為

|E(Fm)|=2m-1,且Δ(Fm)=m,d(u0)=m,d(u1)=d(um)=2,當2≤i≤m-1時,d(ui)=3.

為了刻畫Fm的r-hued染色數的精確值,根據r的取值范圍,分以下3種情形進行討論.

情形 1 1≤r≤2.定義映射c1:V(Fm)→{0,1,2}如下:

c1(u0)=0,

其中,m≥2.

當r=2時,對于ui而言,滿足

2=|c1(N(u0))|≥min{d(u0),2}=2;

當i=1,m時,

2=|c1(N(ui))|≥min{d(ui),2}=2;

當i=2≤i≤m-1時,

2=|c1(N(ui))|≥min{d(ui),2}=2.

從而c1是圖Fm的一個(3,2)-染色,即χ2(Fm)≤3.由引理2知

χ2(Fm)≥min{Δ(Fm),2}+1=

min{m,2}+1=3,從而χ2(Fm)=3.

因為Fm中包含三角形,有χ1(Fm)≥3.由引理1,χ1(Fm)≤χ2(Fm)≤3,所以χ1(Fm)=3,故

χ1≤r≤2(Fm)=3.

情形 2 3≤r≤Δ.定義映射c2:V(Fm)→{0,1,2,…,r}如下:

c2(u0)=0,

其中,m=Δ≥3.

r=|c2(N(u0))|≥min{d(u0),r}={m,r}=r;

當i=1,m時,

2=|c2(N(ui))|≥min{d(ui),2}={2,r}=2;

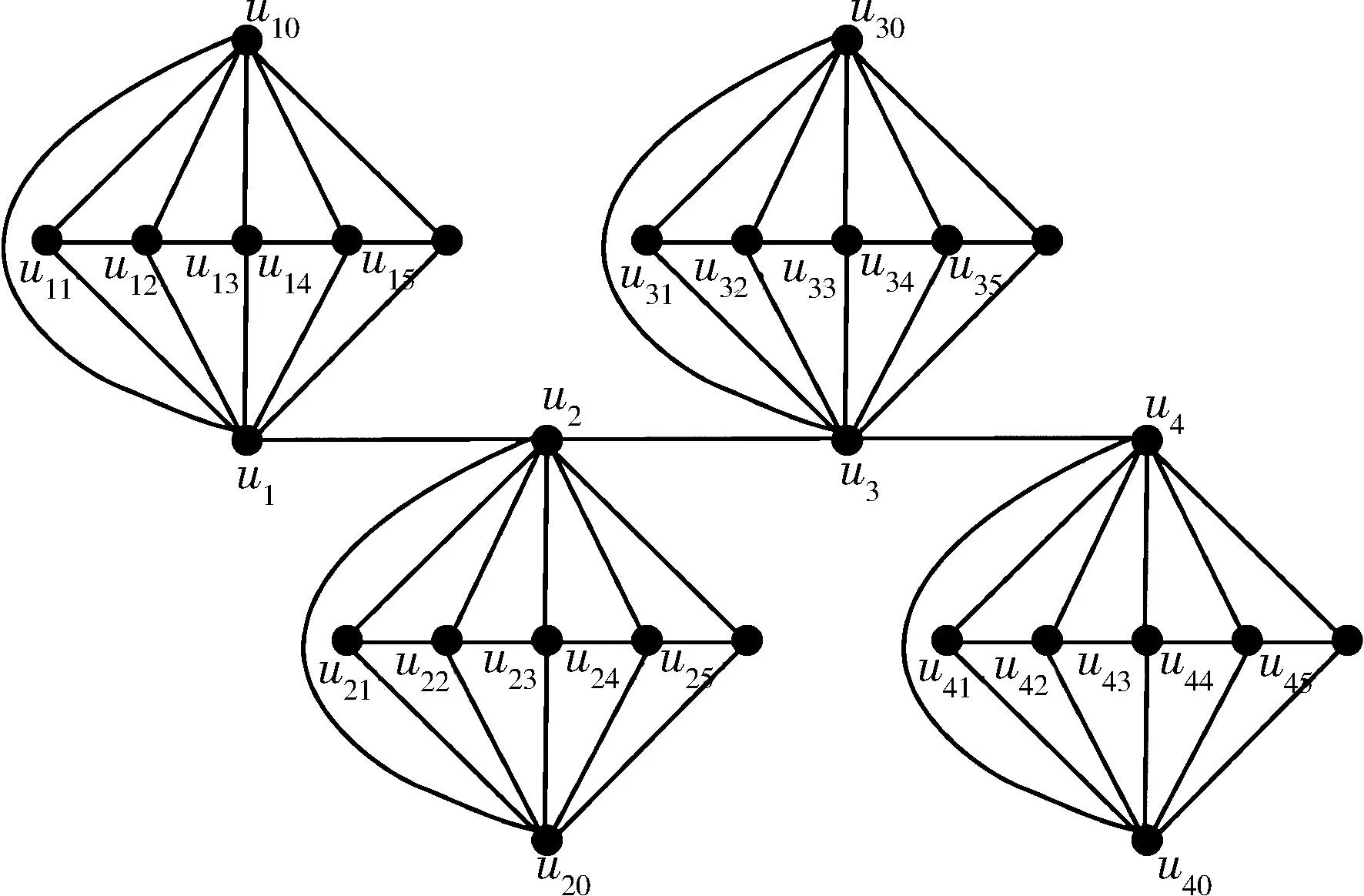
當1

3=|c2(N(ui))|≥min{d(ui),r}={3,r}=3.

從而c2是圖Fm的一個(r+1,r)-染色,即χr(Fm)≤r+1.由引理2知,χr(Fm)≥min{Δ(Fm),r}+1=min{m,r}+1=r+1,從而χr(Fm)=r+1,故

χ3≤r≤Δ(Fm)=r+1.

情形 3r>Δ.定義映射c3:V(Fm)→{0,1,2,…,m}如下:

c3(u0)=0,c3(ui)=i, 1≤i≤m,其中,m≥3.

當i=1,m時,

2=|c3(N(ui))|≥min{2,r}=2,當1

3=|c3(N(ui))|≥min{3,r}=3,

m=|c3(N(u0))|≥min{Δ,r}=Δ=m.

從而c3是圖Fm的一個(m+1,r)-染色,即

χr(Fm)≤m+1.

由引理2知

χr(Fm)≥min{Δ(Fm),r}+1=

min{m,r}+1≥m+1,從而χr>Δ(Fm)=m+1.

2 Pn⊙Fm的r-hued染色數

本節主要研究路Pn和扇圖Fm的corona乘積圖的r-hued染色數.

定理 2設Pn⊙Fm是路和扇圖的corona乘積圖,n≥2,m≥2,則

證明路的頂點集合為

V1(Pn)={v1,v2,…,vn},邊集合為

E1(Pn)={vivi+1|1≤i≤n-1};

扇圖的頂點集合為

V2(Fm)={u0,u1,u2,…,um},邊集合為

E2(Fm)={u0uj|1≤j≤m}∪

{ujuj+1|1≤j≤m-1}.

由此,可以假設Pn⊙Fm的頂點集合為

V(Pn⊙Fm)={vi|1≤i≤n}∪

{uij|1≤i≤n,0≤j≤m},即

|V(Pn⊙Fm)|=n(m+2),邊集合為

E(Pn⊙Fm)={vivi+1|1≤i≤n-1}∪

{viuij|1≤i≤n,0≤j≤m}∪

{ui0uij|1≤i≤n,1≤j≤m}∪

{uijui(j+1)|1≤i≤n,1≤j≤m-1},則|E(Pn⊙Fm)|=3mn+n-1,且當n=2時,Δ(Pn⊙Fm)=m+2;當n≥3時,Δ(Pn⊙Fm)=m+3.P4與F5的corona乘積圖如圖1所示.

圖 1 P4與F5的corona乘積圖

為了刻畫Pn⊙Fm的r-hued染色數的精確值,根據r的取值范圍,分以下3種情形進行討論.

情形 1 1≤r≤3.定義映射c4:V(Pn⊙Fm)→{1,2,3,4}如下:

其中,n≥2,m≥2.

映射c4是圖Pn⊙Fm的一個(4,3)-染色,即χ3(Pn⊙Fm)≤4.由引理2知χr(Pn⊙Fm)≥min{Δ(Pn⊙Fm),3}+1=min{m+3,3}+1=4,從而χ3(Pn⊙Fm)=4.

因為Pn⊙Fm中包含K4,所以χ1(Pn⊙Fm)≥4.由引理1知χ1(Pn⊙Fm)≤χ3(Pn⊙Fm)=4,從而χ1(Pn⊙Fm)=4,而

4=χ1(Pn⊙Fm)≤χ2(Pn⊙Fm)≤χ3(Pn⊙Fm)=4,即χ2(Pn⊙Fm)=4,故χ1≤r≤3(Pn⊙Fm)=4.

情形 2 4≤r≤Δ-1.

子情形 2.1 4≤r≤Δ-2.定義映射

c51:V(Pn⊙Fm)→{1,2,…,r,r+1}

如下:

其中,n≥2,m≥3.

映射c51是圖Pn⊙Fm的一個(r+1,r)-染色,即

χr(Pn⊙Fm)≤r+1.

子情形 2.2r=Δ-1.定義映射

c52:V(Pn⊙Fm)→{1,2,…,r,r+1}

如下:

其中,n≥2,m=r-2≥3.

映射c52是圖Pn⊙Fm的一個(r+1,r)-染色,即

χr(Pn⊙Fm)≤r+1.

由子情形2.1和2.2可得,當4≤r≤Δ-1時,χr(Pn⊙Fm)≤r+1.由引理2知χr(Pn⊙Fm)≥min{Δ(Pn⊙Fm),r}+1=min{m+3,r}+1=r+1,從而χr(Pn⊙Fm)=r+1,故

χ4≤r≤Δ-1(Pn⊙Fm)=r+1.

情形 3r≥Δ.定義映射

c6:V(Pn⊙Fm)→{1,2,…,Δ,Δ+1}

如下.

子情形 3.1 當n=2,m≥3時,

c6(v1)=1,c6(v2)=2,

映射c6是圖Pn⊙Fm的一個(m+3,r)-染色,即

χr(Pn⊙Fm)≤m+3=Δ+1.

子情形 3.2 當n≥3,m≥3時,

映射c6是圖Pn⊙Fm的一個(m+4,r)-染色,即

χr(Pn⊙Fm)≤m+4=Δ+1.

由子情形3.1和3.2可得χr(Pn⊙Fm)≤Δ+1.由引理2知χr(Pn⊙Fm)≥min{Δ(Pn⊙Fm),r}+1=min{Δ,r}+1=Δ+1,從而χr(Pn⊙Fm)=Δ+1,故

χr≥Δ(Pn⊙Fm)=Δ+1.

例 1設Pn⊙Fm是路和扇圖的corona乘積圖,討論n=2或3,m=2,r=4的情形:

1) 當n=2,m=2時,此圖的最大度為4且c(v1)=1,c(v2)=5,c(ui0)=2,c(ui1)=3,c(ui2)=4(i=1,2),即χr=4(Pn⊙Fm)=5.

2) 當n=3,m=2時,此圖的最大度為5且c(v1)=1,c(v2)=5,c(v3)=1,c(ui0)=2,c(ui1)=3,c(ui2)=4(i=1,2,3),即χr=4(Pn⊙Fm)=r+1=5.

3 Cn⊙Fm的r-hued染色數

本節主要研究圈Cn和扇圖Fm的corona乘積圖的r-hued染色數.

定理 3設Cn⊙Fm是圈和扇圖的corona乘積圖,n≥3,m≥3,則

證明圈的頂點集合為

V1(Cn)={v1,v2,…,vn},邊集合記為

E1(Cn)={vivi+1|1≤i≤n-1}∪{v1vn};

扇圖的頂點集合為

V2(Fm)={u0,u1,u2,…,um},邊集合為

E2(Fm)={u0uj|1≤j≤m}∪{ujuj+1|1≤j≤m-1}.

由此,可以假設Cn⊙Fm的頂點集合為

V(Cn⊙Fm)={vi|1≤i≤n}∪{uij|1≤i≤n,0≤j≤m},即

|V(Cn⊙Fm)|=n(m+2),邊集合為

E(Cn⊙Fm)={vivi+1|1≤i≤n-1}∪{v1vn}∪

{viuij|1≤i≤n,0≤j≤m}∪{ui0uij|1≤i≤n,1≤j≤m}∪

{uijui(j+1)|1≤i≤n,1≤j≤m-1},則

|E(Cn⊙Fm)|=3mn+n,且Δ(Cn⊙Fm)=m+3.

為了刻畫Cn⊙Fm的r-hued染色數的精確值,根據r的取值范圍,分以下3種情形進行討論.

情形 1 1≤r≤3.

子情形 1.1 設n是偶數且n≥4,定義映射c71:V(Cn⊙Fm)→{1,2,3,4}如下:

映射c71是圖Cn⊙Fm的一個(4,3)-染色,即

χ3(Cn⊙Fm)≤4.

子情形 1.2 設n是奇數且n≥3,定義

c72:V(Cn⊙Fm)→{1,2,3,4}

如下:

映射c72是圖Cn⊙Fm的一個(4,3)-染色,即

χ3(Cn⊙Fm)≤4.

由子情形1.1和1.2可得χ3(Cn⊙Fm)≤4.由引理2知χ3(Cn⊙Fm)≥min{Δ(Cn⊙Fm),3}+1=min{m+3,3}+1=4,從而χ3(Cn⊙Fm)=4.

因為Cn⊙Fm中包含K4,所以χ1(Cn⊙Fm)≥4.由引理1知χ1(Cn⊙Fm)≤χ3(Cn⊙Fm)=4,從而χ1(Cn⊙Fm)=4,而

4=χ1(Cn⊙Fm)≤χ2(Cn⊙Fm)≤

χ3(Cn⊙Fm)=4,即χ2(Cn⊙Fm)=4,故χ1≤r≤3(Cn⊙Fm)=4.

情形 2 4≤r≤Δ-1.

子情形 2.1 4≤r≤Δ-2,n是偶數.定義映射c81:V(Cn⊙Fm)→{1,2,…,r,r+1}如下:

其中,n≥4.

映射c81是圖Cn⊙Fm的一個(r+1,r)-染色,即

χr(Cn⊙Fm)≤r+1.

子情形 2.2 4≤r≤Δ-2,n是奇數.定義映射c82:V(Cn⊙Fm)→{1,2,…,r,r+1}如下:

其中,n≥3.

映射c82是圖Cn⊙Fm的一個(r+1,r)-染色,即

χr(Cn⊙Fm)≤r+1.

子情形 2.3r=Δ-1,n是偶數.定義映射c83:V(Cn⊙Fm)→{1,2,…,r,r+1}如下:

其中,n≥4,m=r-2≥3.

映射c83是圖Cn⊙Fm的一個(r+1,r)-染色,即

χr(Cn⊙Fm)≤r+1.

子情形 2.4r=Δ-1,n是奇數.定義映射c84:V(Cn⊙Fm)→{1,2,…,r,r+1}如下:

其中,n≥3,m=r-2≥3.

映射c84是圖Cn⊙Fm的一個(r+1,r)-染色,即

χr(Cn⊙Fm)≤r+1.

由子情形2.1～2.4可得,當4≤r≤Δ-1時,χr(Cn⊙Fm)≤r+1.由引理2知χr(Cn⊙Fm)≥min{Δ(Cn⊙Fm),r}+1=min{m+3,r}+1=r+1,從而χr(Cn⊙Fm)=r+1,故

χ4≤r≤Δ-1(Cn⊙Fm)=r+1.

情形 3r≥Δ.

子情形 3.1 當n≡0(mod 3)時,定義映射c91:V(Cn⊙Fm)→{1,2,…,m+3,m+4}如下:

其中,m≥3.

映射c91是圖Cn⊙Fm的一個(m+4,r)-染色,即

χr(Cn⊙Fm)≤m+4.

子情形 3.2 當n≡1(mod 3)時,定義映射c92:V(Cn⊙Fm)→{1,2,…,m+3,m+4}如下:

其中,m≥3.

映射c92是圖Cn⊙Fm的一個(m+4,r)-染色,即χr(Cn⊙Fm)≤m+4.

子情形 3.3 當n≡2(mod 3)時,定義映射c93:V(Cn⊙Fm)→{1,2,…,m+3,m+4}如下:

其中,m≥3.

映射c93是圖Cn⊙Fm的一個(m+4,r)-染色,即χr(Cn⊙Fm)≤m+4.

由子情形3.1～3.3可得,當r≥Δ時,

χr(Cn⊙Fm)≤m+4.

由引理2知χr(Cn⊙Fm)≥min{Δ(Cn⊙Fm),r}+1=min{m+3,r}+1=m+4,從而χr(Cn⊙Fm)=m+4,故χr≥Δ(Cn⊙Fm)=m+4.