電路中的動態變化問題模型分析

馬洪波

(浙江省杭州市臨安區於潛中學)

恒定電流部分涉及電路分析、動態變化和圖像問題三大考點,三者互相關聯,難解難分.其中,動態變化問題是最常考查的電路問題,也是三者的最終表現形式.如果能夠熟練解決電路的動態變化問題,也就意味著基本掌握了恒定電流部分的知識內容.本文就電路中動態變化問題進行模型整合.

1 模型構建

恒定電流電路中的動態變化問題指的是在外電路中當某一部分電路的物理量變化時,會引起電路中其余部分發生一系列變化的情況.電路中的變化包括整個電路各個部分的電壓、電流、功率等的變化,分析時需要應用到的電路知識包括:電壓、電流和功率的相互關系;閉合電路歐姆定律和部分電路歐姆定律;電動勢、電容、振蕩電路、電場或磁場中的帶電粒子運動相關公式等.因為涉及知識點多,且往往與其他知識點結合考查,所以難度較高.下面,我們先來看一下電路中的動態變化模型.

模型 一平行板電容器的兩個金屬板水平放置,連接在如圖1 所示的電路中,開關S 閉合后,電容器極板之間一個質量為m、電荷量為q的小微粒恰好靜止.已知電源的電動勢和內阻分別為E和r,G 是一臺靈敏電流計.以下說法中正確的是( ).

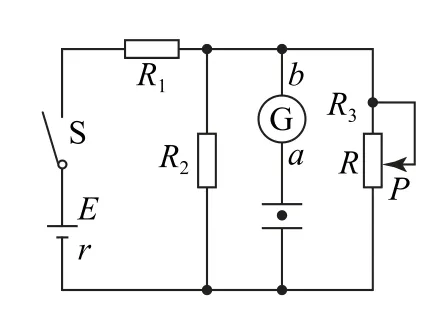
圖1

A.滑動變阻器滑片P向上移動時,靈敏電流計G 中通過的電流方向是b→a,小微粒向上加速運動

B.滑動變阻器滑片P向下移動時,靈敏電流計G 中通過的電流方向是b→a,小微粒向下加速運動

C.滑動變阻器滑片P向上移動時,靈敏電流計G 中通過的電流方向是a→b,小微粒靜止不動

D.當斷開開關S后,靈敏電流計G 中無電流通過,帶電小微粒靜止不動

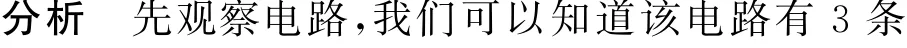
當開關S斷開時,原電路中3條支路組成閉合電路,電容器在其中充當電源,故電容器會迅速放電直至電荷量為0,因此靈敏電流計G 中有方向為a→b的電流,帶電小微粒向下加速運動,選項D 錯誤.

特征分析 牽一發而動全身是該模型的最大特征.比如本題,滑動變阻器滑片的移動、開關的狀態等都能改變整個電路的狀態.另外,該模型常見的變化類型還有多向開關模型、磁場變化模型、帶電液滴的增減(即電荷量變化)模型等.

2 方法總結

該模型解題的核心知識是閉合電路的歐姆定律,圍繞該核心,可以總結出以下4種解法,以供選擇.

解法1 直觀法

直觀法適合較為簡單的動態變化問題.具體做法是應用支路電路中的電壓、電流和電阻的關系直接得出結論,當電路中某一電阻變化時:1)與之串聯的電學元件中的電流隨該電阻阻值的變大(變小)而變小(變大),電壓隨該電阻阻值的變大(變小)而變小(變大).2)與之并聯的電學元件中的電流隨該電阻阻值的變大(變小)而變大(變小),電壓隨該電阻阻值的變大(變小)而變大(變小).以上規律可總結為“串反并同”.

解法2 程序法

程序法適合所有電路動態變化類問題.具體解題思路可總結為“部分→整體→部分”,即先從引起變化的源頭分析,判斷該元器件所在部分的電壓、電流和電阻的變化情況;然后判斷該變化對整個電路,即干路的影響;最后根據干路的變化情況判斷局部電路的情況.總結為思維導圖如圖2所示.

圖2

解法3 特殊值法

特殊值法只適合某些雙臂環路問題.解題時可以代入某些特殊值,從而快速得出結論.

解法4 極值法

極值法只適用于由于滑動變阻器接入電路中的阻值發生變化而(或可視為滑動變阻器的類似阻值變化)引起電路變化的問題.解題時可嘗試將滑動變阻器實際接入電路中的阻值取兩個極端值(0和滿阻值)代入求解.

解題提醒 具體問題具體分析是我們最常聽到的一句話,在學習中也是如此.雖然模型總結起來簡單清晰,但在面對具體問題時,還有很多細節需要我們注意,現總結如下:1)分清總功率、輸出功率和損耗功率.若馬虎大意,容易錯用公式出現錯解.2)分清功率和效率的關系.效率最大時,輸出功率未必最大.3)分 清U和ΔU、I和ΔI、U/I和ΔU/ΔI的 差 異.4)正確認識特殊元器件,比如電容器、二極管、振蕩器等,它們對電路的特殊影響一定要記清.

3 例題賞析

例 如圖3所示,是一個實驗電路圖,其中電源電壓220V,R1、R2、R3均為定值電阻.由于標簽損壞,三個定值電阻的阻值不明,只知道可能的阻值為44 Ω、88Ω、176 Ω、220 Ω.保 持 開關S 閉合,在開關S1和S2同時斷開和閉合的狀態下,電流表的讀數大小比值為1∶10.若知道該電路消耗的電功率有4種可能的情況,其中消耗的最大值為1100 W.求:

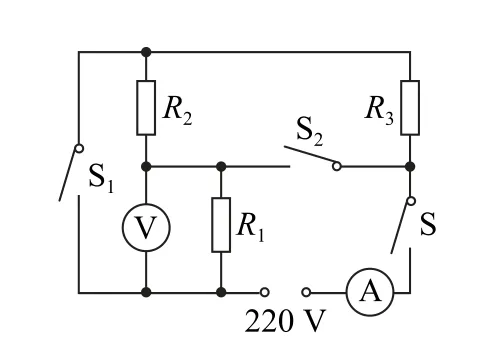
圖3

(1)定值電阻R2的阻值;

(2)在保持開關S閉合,開關S1和S2同時斷開的狀態下,電壓表讀數的可能值.

綜上計算及題給信息,可知3個定值電阻的阻值應在88Ω、176Ω、176Ω 中選擇.根據3個開關的通斷可知分以下4種情況:①3個開關都閉合;②開關S閉合,S1、S2斷開;③開關S、S1閉合,S2斷開;④開關S、S2閉合,S1斷開.4種情況對應的電路圖分別如圖4所示.

圖4

(2)當開關S閉合,S1、S2斷開時,等效電路圖如圖4中②所示,電壓表測R1兩端電壓,有U＝I串R1.由(1)知R1的阻值可能為88Ω 和176Ω,代入數據可知電壓表的示數可能為44V 和88V.

總之,解答電路的動態變化問題時,只要對各個元器件的性質做到正確理解,對電路涉及的物理知識(尤其是歐姆定律)做到熟練掌握,同時保持清晰的思維、采用縝密的推理,就能輕松解決問題.