新能源并網電站涉網性能無功優化方法

卜曉坤

（電力規劃設計總院，北京 100120）

0 引 言

在化石能源日漸枯竭的當今社會，新能源已經成為了一種應用范圍極為廣泛的能源，大量新能源并入電網后卻給電網的穩定運行帶來了巨大的阻礙。大量的新能源并網電站會導致電網的潮流分布和暫態穩定性變差，進而導致系統原有的運行成本增加，輸電系統穩定性降低，原有的繼電保護設施難以繼續保證新能源并網后的系統性能。為改善并網電站涉網性能，需要對其進行無功優化。通過靈活多變的網絡拓撲結構，保證可再生能源對并網電站的支撐作用。優化無功潮流，在降低網損、提高電能質量的同時，對多種可控資源進行調整與控制，進而使所有已經并網的新能源能夠獲得更積極的消納路徑。文獻[1]在分布式電源以及儲能系統之間，設計了一種具備恒功率特性的無功優化模型，該模型可以獲得更小的計算偏差，同時結合動態均衡方法滿足多時段的無功補償。文獻[2]所設計的電力系統在風電、光伏等新能源的加入下，建立了一個新能源電站集群的無功優化模型，該模型使用二階錐凸松弛算法和分段線性化算法，解決了電壓控制不足、系統經濟性較差的問題。本文結合上述文獻，設計了一種新能源并網電站涉網性能無功優化方法。

1 設計新能源并網電站潮流計算方法

在新能源并網的潮流計算中，首先需要確定不同新能源電源的等效模型。普通異步發電機的并網系統具備結構簡單、成本低廉的優點，但是其在工作過程中不具備勵磁設備，因此需要通過在發電機一端安裝分組電容器的方式進行無功補償。此時其等值電路可以表示為

式中：Pm表示新能源發電機在等值電路中的發電功率；Im表示電路電流；R表示電路電阻；Up表示電源電壓；Qm表示新能源發電機在等值電路中的輸出功率；Fs表示潮流計算的轉差率；Nx表示轉子的有功出力；Nd表示轉子的無功出力。在該等值電路下，傳統配電網在無新能源時的潮流計算一般使用前推后代法。第1步需要將配電網的平衡節點初始化，此時電壓的標幺值可以表示為1 p.u.，且電壓的迭代次數為0。第2步開始進行電流的前推，根據計算得到的節點電壓以及國內功率損耗，可以結合負荷功率獲取全網的功率分布情況，并完成對網絡一端的功率計算。第3步需要對回代過程進行處理，在等值網絡電路上計算支路功率，結合電壓的升降過程，獲取節點電壓的幅值與相位。前推回代結束后，需要在第4步中檢驗潮流計算的整個過程是否收斂，通過判斷標準確定最終數值是否小于給定值[3]。若沒有達到收斂標準，則需要在迭代中循環，直至達到收斂標準為止。在新能源的潮流計算中，需要以上述前推回代為基礎，新增新能源節點。不同的新能源類型具備不同的隨機特性，其并網方式均不相同，具體如表1所示。

表1的并網方法中，分別列舉光伏發電、風能發電、地熱能發電、潮汐能發電以及化學電池發電5個類型的新能源并網方法[4]。在新增節點中，需要分別建立新能源的隨機特性模型，在此過程中進行等值化處理。在不斷迭代下獲取電壓相量，并計算新能源節點電流的無功功率為

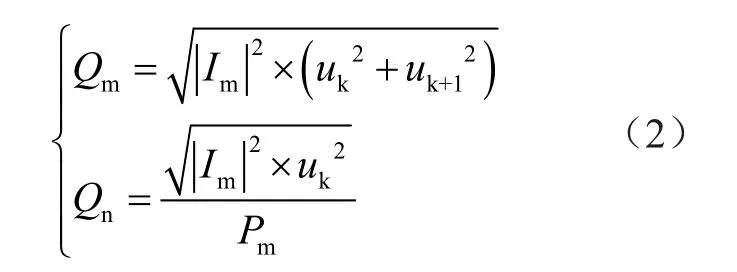
式中：Qm表示DC/AC逆變器作用下電流的無功功率；Qn表示同步發電機作用下電流的無功功率；uk和uk+1分別表示2個緊鄰的迭代過程的電壓。在該等值化模型下，可以得到新能源潮流計算的具體流程如圖1所示。

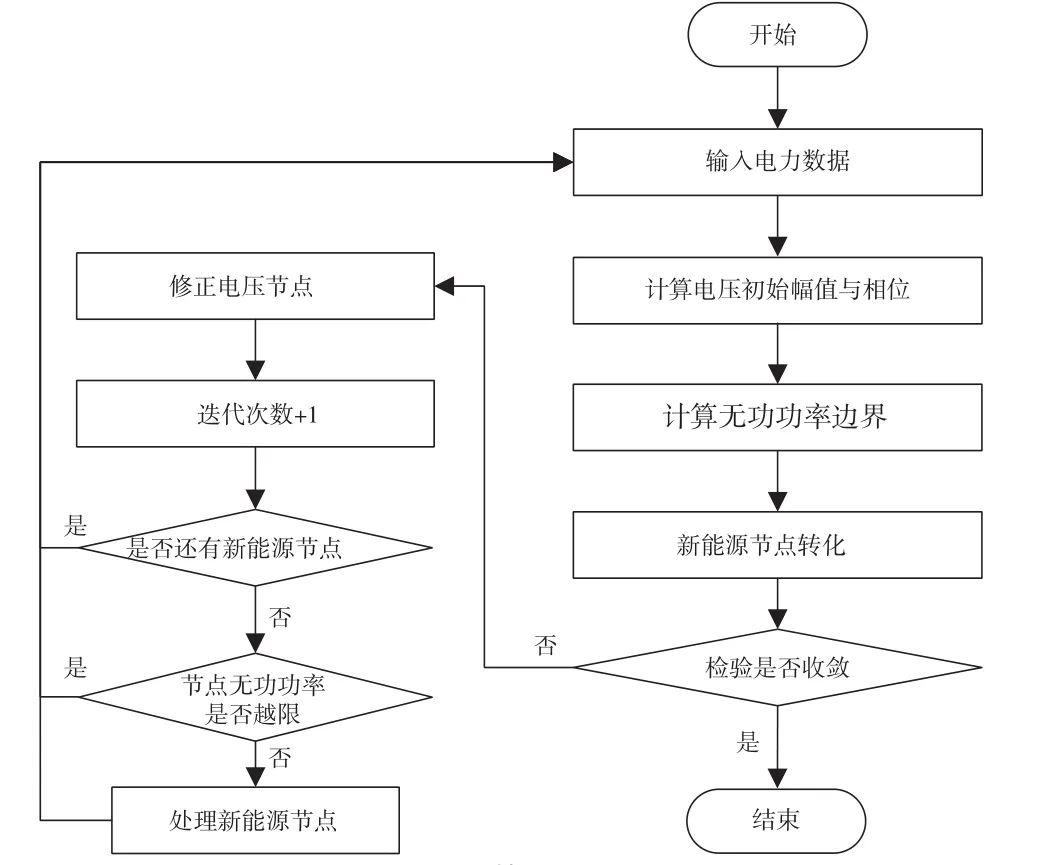
圖1 算法流程

圖1中，通過是否收斂判斷算法是否結束，在此過程中需要使用電壓變化量作為收斂標準，其計算公式為

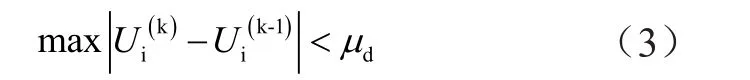
2 建立涉網性能無功優化模型

結合潮流計算的結果，建立涉網性能無功優化模型，需要首先建立新能源接入網絡的目標函數。在考慮經營經濟性和電壓穩定性的同時，依據有功功率損耗的最小值和負荷節點電壓偏差的最小值得到目標函數為

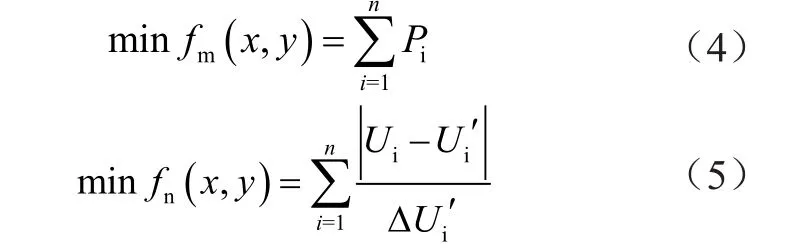
式中：fm(x,y)表示有功功率損耗的函數值；fn(x,y)表示負荷節點電壓偏差的函數值；Pi表示有功功率；Ui表示負荷節點上的電壓值；Ui'表示負荷節點的電壓參考值。在這2個目標函數中，結合不同節點的電壓以及有功功率，可以得到約束條件為

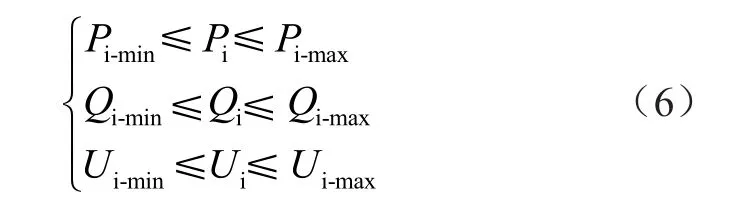
式中：Qi表示無功功率；Pi-min和Pi-max表示有功功率的下界與上界；Qi-min和Qi-max表示無功功率的下界與上界；Ui-min和Ui-max則分別表示節點電壓的下界與上界。根據負荷節點的負載電壓，可以得到負載電壓與傳輸負載的約束條件為

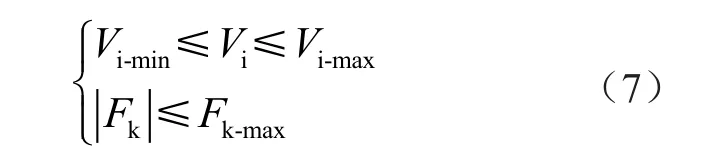
式中：Vi表示負荷節點的負載電壓；Fk表示負荷節點的傳輸負載；Vi-min和Vi-max分別表示負載電壓的下界與上界；Fk-max則表示傳輸負載的上界。根據上述目標函數以及約束條件，可以對新能源并網電站的涉網性能進行無功優化，并建立一個優化模型[5]。通過有功功率損耗和負荷節點電壓偏差，優化并網電站的性能。

3 算例分析

3.1 節點設置

在配電網中，無功功率的影響非常大，本實驗對上文設計的新能源并網電站涉網性能無功優化進行仿真分析，并設置一個仿真節點系統。以12節點的鏈式結構為基礎，其系統模型如圖2所示。

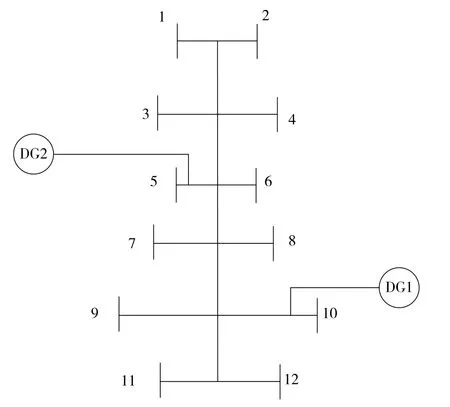
圖2 12節點鏈式結構配電系統模型

在圖2所示的配網系統模型中，共存在12個節點，其中節點5和節點10處分別存在1個新能源并網DG。在該系統內，并網DG的有功功率為250 kW，無功功率的范圍為0～1 000 kvar。

3.2 2種極端條件下電網工作狀態

在上述系統模型中，設定2種極端條件。第一，線路負荷調整為最大值，此時2個新能源并網電源會因為故障或者其他原因而退出工作狀態，即此時DG1和DG2的有功與無功功率均為0。第二，線路負荷調整為輕載狀態，設定10%功率輸出為額定負荷，DG1和DG2這2個新能源系統運行正常，有功出力達到最大，無功出力為0。在上述2個極端條件下，繪制配網節點系統模型的初始電壓曲線如圖3所示。

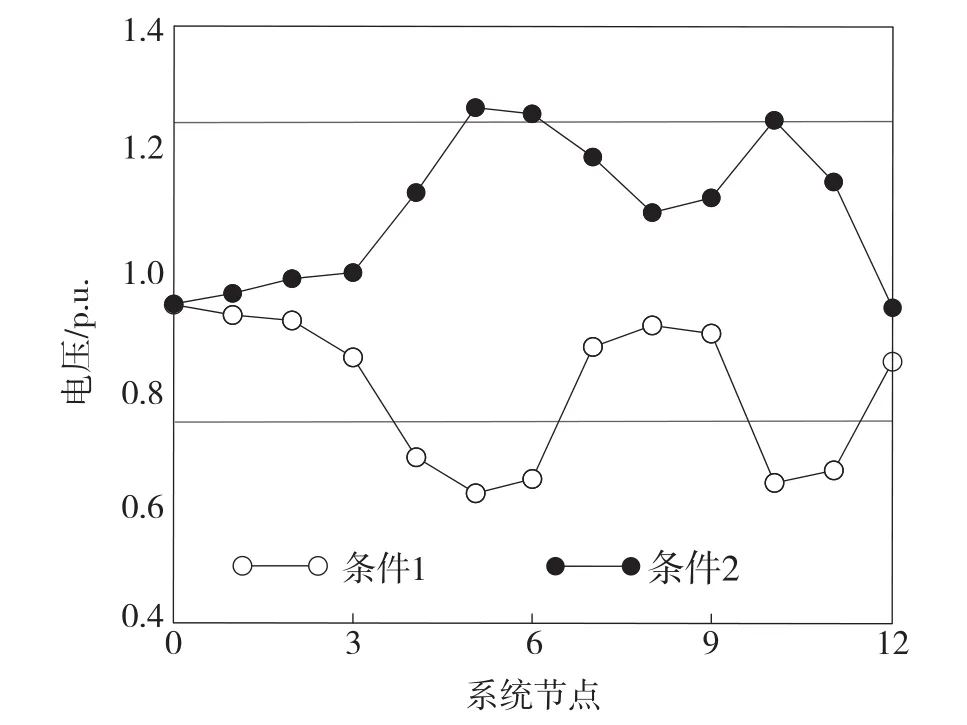
圖3 初始電壓曲線

通過圖3所示的仿真結果可知，在條件1中，有一些節點（如節點4、節點5、節點6、節點10、節點11）會越過電壓下限。在條件2中，也有少部分節點（如節點5、節點6、節點10）越過了電壓上限。

3.3 極端條件優化后效果

使用上述方法對2種極端工況的電壓進行優化，可以得到優化效果如圖4所示。

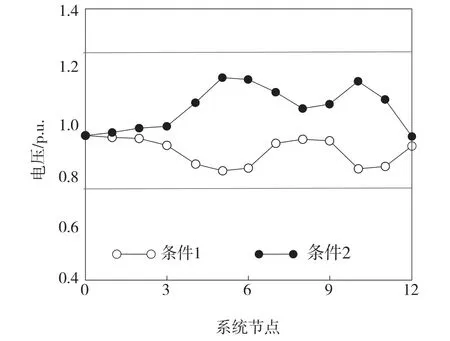
圖4 優化效果圖

如圖4所示，經過優化處理后，2個極端條件下的系統節點電壓均在2道界限之間。其中，條件1經過無功優化后的系統電壓偏差之和為0.52，條件2的電壓偏差之和則為0.88，二者均滿足新能源并網電站對電壓質量的需求，且本文方法很好地解決了系統節點越過電壓上限與下限的問題。

3.4 算法收斂特性對比

設置粒子規模為100，最大迭代次數為700。學習因子a1和a2相同，均為0.5；粒子速度的區間為[-5，5]，慣性權重的最大值與最小值分別為0.8和0.4，分檔系數則為300。分別使用本文方法、動態均衡凸-凹步驟法、有功與無功耦合特性方法對上述系統節點進行迭代優化，可以得到適應度函數值如圖5所示。

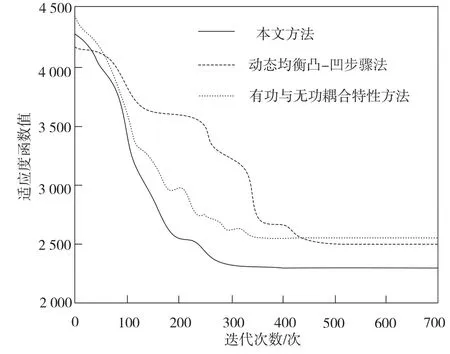
圖5 算法收斂特性曲線

如圖5所示，在700次迭代中，3種方法均順利完成了對算法的尋優。其中本文方法在300次時就得到了適應度函數的最優值，動態均衡凸-凹步驟法在500次迭代時尋優結束，有功與無功耦合特性方法則在400次時迭代結束。這3種方法的對比中，本文方法的適應度函數值明顯優于其他2種算法。

由此可見，本文設計的新能源并網電站涉網性能無功優化方法能夠解決極端條件下的電壓偏差過大問題，且在與其他2種方法的對比中，明顯性能更好。

4 結 論

電壓越限問題一直是新能源并網的重難點，本文設計了一種新能源并網電站涉網性能無功優化方法，該方法可以較好地解決極端環境下的電壓越限問題，同時在與其他方法的對比中可知其效果更好。通過該無功優化方法，可以將新能源并網的電壓偏差約束在標準范圍之內，該范圍內的電網電能質量已經能夠滿足新能源的穩定使用。在接下來的研究中，可以繼續使用本文的方法，對串聯電抗器進行無功優化，探究沖擊電流與串聯方式的應用環境，并對算法進行進一步的改進與優化。