圓弧輪廓銑削最大刀具補償半徑的確定方法

成建群

（蘇州健雄職業技術學院 中德工程學院，太倉 215411）

數控刀具路徑規劃直接影響加工質量和加工效率。通過刀具半徑補償設置自動偏置，可避免大量軌跡偏置帶來的復雜坐標計算[1]。另外，直接采用零件輪廓坐標編制刀具路徑程序，可以利用刀補功能直接去除毛坯加工余量，簡化編程過程[2]。對于復雜曲面加工，可以通過優化補償方法適應曲面加工要求[3-4]。針對零件特殊表面的加工要求，可以充分運行刀具補償原理，優化補償算法，拓展刀具補償的應用范圍，改善加工質量[5-6]。在多軸加工過程中，刀軸矢量多變，但仍可實現刀具補償[7-8]。刀具補償編程是銑削過程中的基本方法，在運用刀具補償編程時需要選用合適的刀具。刀具半徑直接關系刀具的剛度，影響加工質量。刀具直徑大，可以選用更高效的切削參數，提高加工效率，降低加工成本。

在銑削過程中，刀具半徑與最小的零件輪廓半徑有密切關系。零件輪廓半徑小于刀具半徑時，該輪廓不能進行切削。刀具補償半徑根據刀具半徑設定，在不留加工余量的情況下，刀具補償半徑等于刀具半徑；當留有加工余量時，刀具補償半徑大于刀具半徑。所以，刀具最大半徑小于等于刀具最大補償半徑。刀具最大補償半徑決定了刀具最大半徑。在不考慮通過修改刀補來添加余量的情況下，刀具最大半徑就是刀具最大補償半徑。

在數控加工過程中，通常以零件尺寸計算坐標，并添加刀具補償指令完成編程，由數控系統自動計算偏置，完成零件輪廓加工。鑒于數控系統算法的原因，刀具半徑將比零件輪廓半徑更小。西門子840D系統是當前主流數控系統之一，應用廣泛。本文以西門子840D系統為基礎，研究零件輪廓半徑與最大刀具半徑之間的關系。

1 問題的提出

為了在保證一般性的同時簡化問題，選用三軸銑削加工臺階外輪廓面零件進行研究。因外凸圓弧零件輪廓不影響刀具尺寸，這里僅僅考慮內凹槽圓弧零件輪廓，零件如圖1所示。該圖毛坯尺寸為80 mm×80 mm×20 mm，銑削臺階深度為2，三段圓弧凹槽直徑均為Φ20 mm。左側圓弧輪廓圓心在輪廓線上，中間圓弧輪廓圓心在輪廓線內側，右側圓弧輪廓圓心在輪廓線外側。

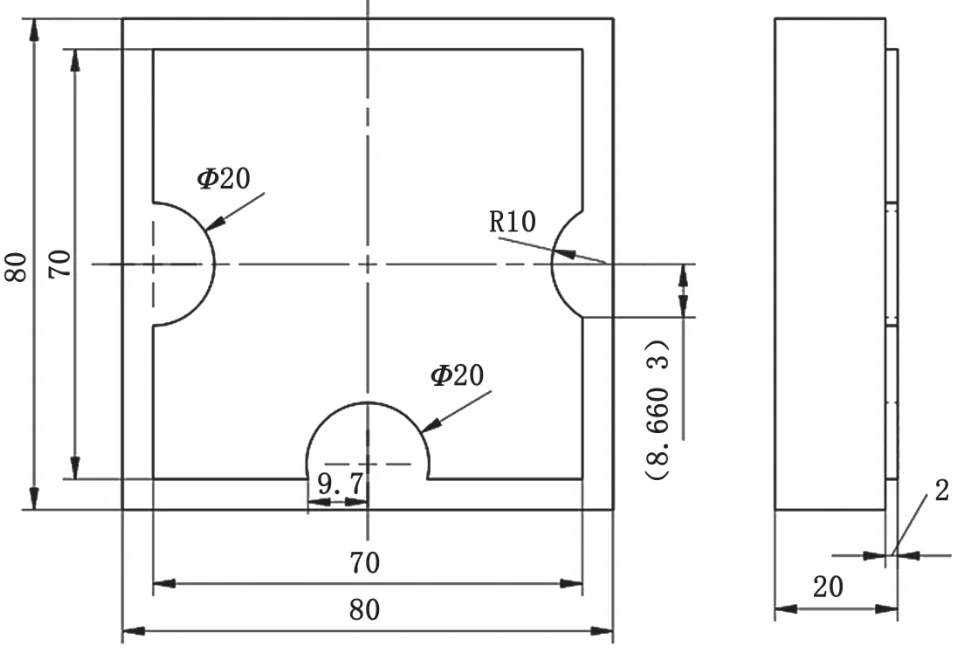
圖1 零件結構（單位：mm）

現選用西門子840D系統，刀具選用Φ16 mm銑刀，利用Vericut軟件建立測試環境。測試環境主要設置如表1所示，控制系統選用sin840d。

表1 Vericut軟件測試環境主要設置

仿真結果如圖2所示，3個Φ20 mm圓弧輪廓僅僅完成了2個，其中1個并未按要求完成，僅表現為Φ16 mm刀具直徑的輪廓。進一步可以查看刀路圖，如圖3所示，其中有1處出現折線，但并未出現Φ20 mm圓弧輪廓加工刀路。

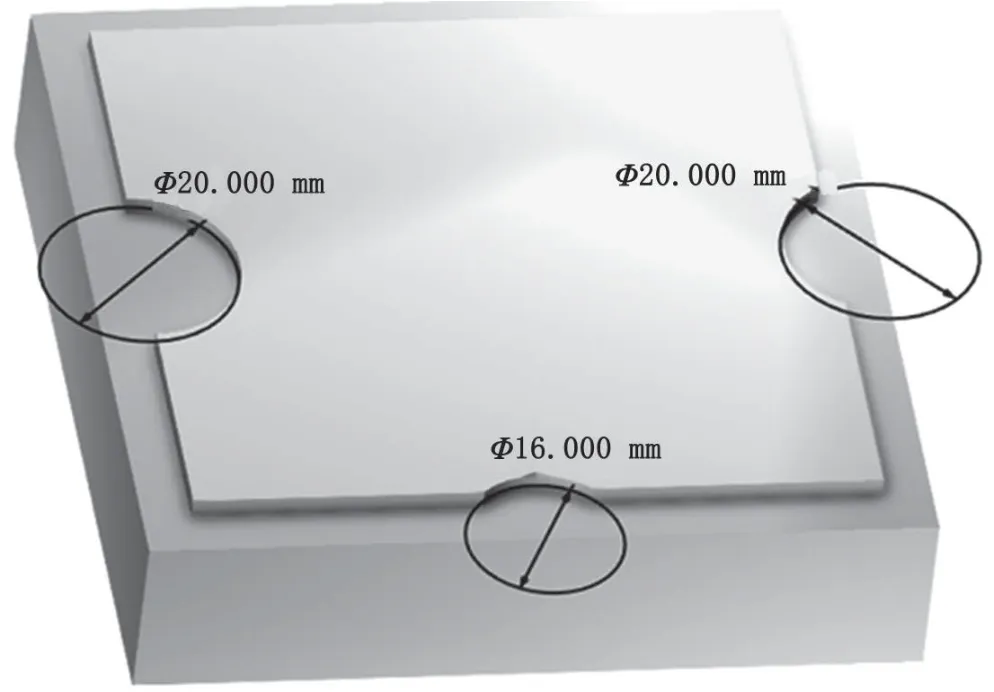
圖2 Φ16 mm刀具仿真結果

圖3 Φ16 mm刀具仿真刀路

可見，當圓弧輪廓圓心在輪廓線外側或在輪廓線上時，刀具最大直徑為圓弧輪廓直徑；當圓弧輪廓圓心在輪廓線內側時，刀具最大直徑小于圓弧輪廓直徑，具體數值需要建立數學模型進行分析。

2 數學模型建立

程序中按逆時針圓弧方向編制，坐標由A點到B點，圓心為O。因刀具偏置，A點時，刀具圓心向左和向下都偏移距離d。切線方向進入圓弧，進入圓弧第一個點A對應刀具中心O1，切線長度為d，由此可以得到刀具中心由K點沿切線進入圓弧輪廓。切出輪廓與切入輪廓符合軸對稱關系，所以刀具Φd由P1到P2銑削圓心為O圓弧輪廓ΦD，形成銑削原理輪廓，如圖4所示。

圖4 銑削原理輪廓

因圖形對稱，選取右側進行分析，建立數學模型。對稱中線交K處水平線于T，A處豎直線交水平線TK于N，延長OA、TK交于P，如圖5所示。其中，輪廓半徑為R，刀具半徑為r，輪廓開口距離為TK，有

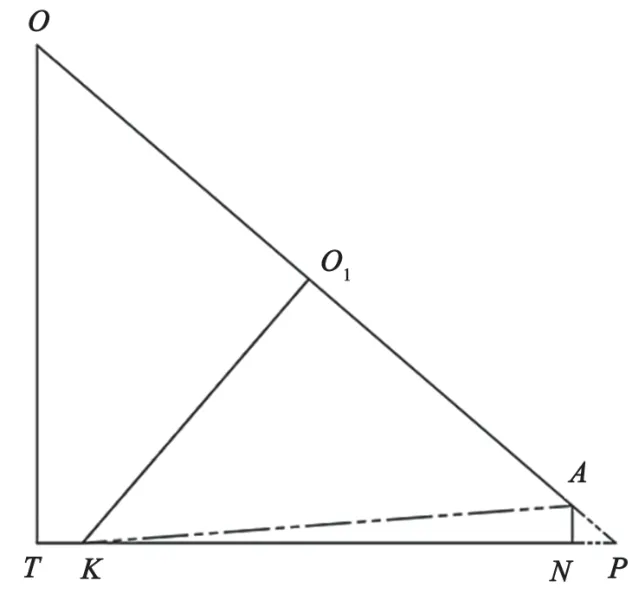
圖5 數學模型幾何

設TK為x，有

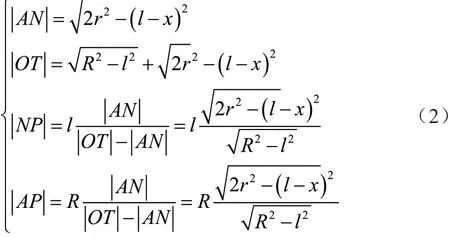
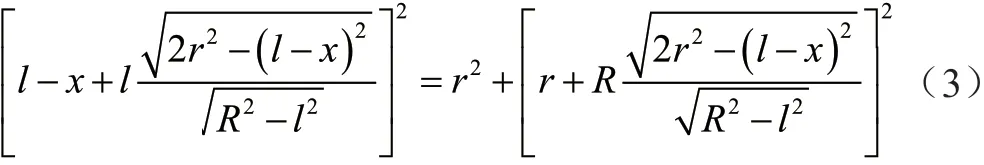
在直角△KPO1中應用勾股定理，得到

求解得到

為了刀具能完成刀補過程，必須x≥0，得到

因刀具半徑必須小于孔半徑，得到

式中：r為有效銑刀半徑；R為圓弧輪廓半徑；l為圓弧輪廓半開口寬度。

式（6）在圓弧輪廓圓心在輪廓線內側有效。當圓弧輪廓圓心在輪廓線上時，式（6）同樣實用。當圓弧輪廓圓心在輪廓線外側時，式（6）失去意義。

3 實驗驗證

依照式（6），將參數R=10和l=9.7代入驗證，得到rmax=7.996，最大刀具直徑為15.992 mm，如圖6所示。

圖6 最大刀具驗證

為了便于說明問題，將刀具半徑增加0.001 mm進一步驗證，結果如圖7所示，未出現Φ20 mm圓弧輪廓加工，刀具偏置失敗。

圖7 超出最大刀具驗證

4 結語

在輪廓銑削加工過程中，運用刀補編程并選擇最大刀具半徑是有效的工作方法，能極大提高工作效率，保證工作質量，降低加工成本。針對圓弧輪廓加工提出了最大刀具半徑計算數學模型，并推導了計算公式。經過西門子840D系統仿真驗證，最大刀具半徑計算結果符合預期，并有力解決了過大半徑刀具無法獲得圓弧輪廓加工刀路的問題，說明最大刀具半徑計算公式正確有效。