基于磁偶極子的2階磁場(chǎng)梯度張量縮并方法

江勝華

(西南大學(xué) 工程技術(shù)學(xué)院，重慶 400715)

0 引言

磁性目標(biāo)的磁場(chǎng)梯度張量定位技術(shù)，作為一種被動(dòng)的定位技術(shù)，具有更豐富更深入的特征信息，包括梯度、張量不變量、特征值和模量等，其最大的優(yōu)點(diǎn)是可以很大程度上克服地球磁場(chǎng)等背景磁場(chǎng)的影響，且不易受測(cè)量系統(tǒng)中朝向誤差的影響，可以提高對(duì)磁性目標(biāo)的定位精度[1-5]。其中，磁場(chǎng)梯度張量的不變量、模量和特征值等，與坐標(biāo)軸方向無(wú)關(guān)，非常適合磁性目標(biāo)的實(shí)時(shí)定位[6-8]，已逐漸應(yīng)用在水下/地下爆炸物探測(cè)、水下磁性物體探測(cè)、入侵物體探測(cè)、室內(nèi)定位、體內(nèi)微型診療裝置定位[9-10]等多個(gè)領(lǐng)域。另一方面，鐵磁金屬試件可視為無(wú)數(shù)個(gè)微小的磁偶極子的組合，微小的磁偶極子與磁場(chǎng)傳感器之間的關(guān)系可近似借鑒磁場(chǎng)定位的相關(guān)理論，磁場(chǎng)梯度張量可應(yīng)用在金屬缺陷、銹蝕、應(yīng)力等損傷檢測(cè)技術(shù)[11-12]。將磁場(chǎng)梯度張量的不變量、模量和特征值等進(jìn)一步處理后，可得到更加豐富、細(xì)致和深入的定位特征信息。隨著全張量磁力梯度儀的研制成功，為了適應(yīng)不同的定位情景，也出現(xiàn)了各種不同構(gòu)造和組合的全張量磁力梯度儀[13-14]。相應(yīng)地，諸多學(xué)者發(fā)展了1階磁場(chǎng)梯度張量的測(cè)量原理和算法，且已經(jīng)應(yīng)用在不同的領(lǐng)域。目前2階磁場(chǎng)梯度張量亦開始逐漸應(yīng)用在磁性物體的定位。Schmidt等[15]認(rèn)為2階磁場(chǎng)梯度張量比1階磁場(chǎng)梯度張量在磁測(cè)反演時(shí)具有更高的分辨率。Clark[16]結(jié)合2階和1階磁場(chǎng)梯度張量計(jì)算了磁場(chǎng)梯度張量的特征值和不變量的導(dǎo)數(shù)，并應(yīng)用在管道定位和礦床的幾何形態(tài)及鉆孔交點(diǎn)的定位，磁場(chǎng)反演結(jié)果與實(shí)際情況一致。Sui等[17]采用安裝在一個(gè)旋轉(zhuǎn)圓盤上的磁傳感器進(jìn)行了2階磁場(chǎng)梯度張量的測(cè)量，認(rèn)為2階磁場(chǎng)梯度張量和1階磁場(chǎng)梯度張量相結(jié)合使用，在一定程度上可降低定位時(shí)非唯一解和非真實(shí)解導(dǎo)致求解的模糊性。Li等[18]提出一種2階磁場(chǎng)梯度測(cè)量系統(tǒng)，并采用2階磁場(chǎng)梯度張量和歐拉方程進(jìn)行磁場(chǎng)定位，結(jié)果表明2階磁場(chǎng)梯度張量具有更強(qiáng)的消除背景磁場(chǎng)和抗干擾的能力。張濤等[19]通過(guò)十字型陣列、六面體陣列及9個(gè)傳感器形成的菱形陣列3種全張量磁傳感系統(tǒng)，在2 m×2 m的正方形區(qū)域內(nèi)進(jìn)行數(shù)值模擬，比較了1階和2階磁場(chǎng)梯度張量，結(jié)果顯示：在消除地磁場(chǎng)方面，2階磁場(chǎng)梯度張量更優(yōu)；在消除干擾噪聲方面，1階磁場(chǎng)梯度張量略優(yōu)。由于全張量磁力梯度儀的研制成功及發(fā)展，研究2階磁場(chǎng)梯度張量，并與1階磁場(chǎng)梯度張量結(jié)合使用，在磁場(chǎng)定位中將具有重要的研究意義和應(yīng)用價(jià)值。

鑒于1階和2階磁場(chǎng)梯度張量測(cè)量設(shè)備的逐漸發(fā)展，同時(shí)2階磁場(chǎng)梯度張量在磁測(cè)反演擁有更高的分辨率，處理特征值和不變量時(shí)具有更豐富、更細(xì)致的信息，更強(qiáng)的消除背景磁場(chǎng)和抗干擾的能力，可降低定位時(shí)非唯一解和非真實(shí)解導(dǎo)致求解的模糊性等多方面的優(yōu)點(diǎn)，針對(duì)2階磁場(chǎng)梯度張量的理論尚不夠完善的現(xiàn)狀，本文提出基于磁偶極子的2階磁場(chǎng)梯度張量縮并方法，包括全局縮并和局部縮并的方法，提出2階磁場(chǎng)梯度張量的全局模量和局部模量的計(jì)算公式，進(jìn)行仿真分析，研究全局模量和局部模量及相關(guān)參數(shù)的三維空間分布規(guī)律，給出相關(guān)參數(shù)的近似計(jì)算公式，并比較2階和1階磁場(chǎng)梯度張量及模量隨距離的規(guī)律。

1 基于磁偶極子的2階磁場(chǎng)梯度張量

如磁性物體簡(jiǎn)化為磁偶極子，在測(cè)試系統(tǒng)處激發(fā)的磁感應(yīng)強(qiáng)度矢量[20]為

(1)

式中：μ0為介質(zhì)磁導(dǎo)率；m為磁性目標(biāo)的磁矩m=(mx,my,mz)，其中mx、my和mz分別為磁矩m沿著x軸、y軸和z軸3個(gè)方向的分量；r為磁偶極子至測(cè)量系統(tǒng)的位置矢量，r為r的模，r=|r|，即磁偶極子至測(cè)量系統(tǒng)的距離。磁感應(yīng)強(qiáng)度矢量B可以用笛卡爾分量表示，即沿x軸、y軸和z軸3個(gè)方向的磁感應(yīng)強(qiáng)度Bx、By和Bz。

磁偶極子的1階磁場(chǎng)梯度張量[4,17]為

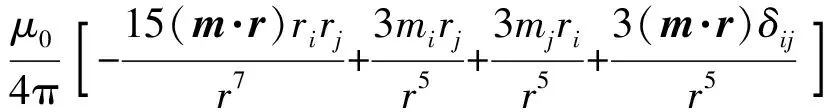
(2)

(3)

式中：i,j=x,y,z。

1階磁場(chǎng)梯度張量G中共有9個(gè)參數(shù)，即Bxx、Bxy、Bxz、Byx、Byy、Byz、Bzx、Bzy和Bzz，分別為磁感應(yīng)強(qiáng)度Bx、By和Bz沿x軸、y軸和z軸3個(gè)方向的梯度。9個(gè)參數(shù)中僅有5個(gè)獨(dú)立的參數(shù)，即Bxx、Bxy、Bxz、Byy和Byz。

磁偶極子的1階磁場(chǎng)梯度張量的全局模量CG為

(4)

式中：Gij表示矩陣Gij中的參數(shù)。

1階磁場(chǎng)梯度張量的全局模量與磁偶極子的磁矩的模、磁偶極子至測(cè)量系統(tǒng)的距離等之間的關(guān)系[21-22]為

(5)

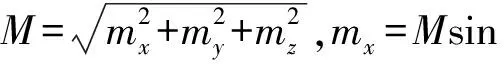
磁偶極子的2階磁場(chǎng)梯度張量[17]為

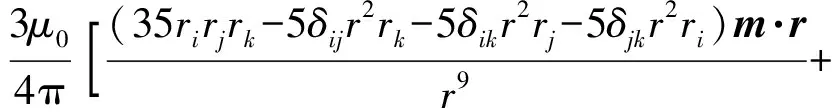
(6)

δ=(δil,δjl,δkl)

(7)

式中：k,l=x,y,z。

磁偶極子的2階磁場(chǎng)梯度張量展開成3個(gè)矩陣Hx、Hy和Hz：

(8)

式中：主對(duì)角元素滿足：

Hxxx+Hyyx+Hzzx=0

(9)

Hx矩陣中共9個(gè)參數(shù)，但僅有5個(gè)獨(dú)立的參數(shù)，即Hxxx、Hxyx、Hxzx、Hyyx和Hyzx。

(10)

式中：主對(duì)角元素滿足：

Hxxy+Hyyy+Hzzy=0

(11)

Hy矩陣中共9個(gè)參數(shù)，但僅有5個(gè)獨(dú)立的參數(shù)，即Hxxy、Hxyy、Hxzy、Hyyy和Hyzy。

(12)

式中：主對(duì)角元素滿足：

Hzzz=-Hxxz-Hyyz

(13)

Hz矩陣中共9個(gè)參數(shù)，但僅有5個(gè)獨(dú)立的參數(shù)，即Hxxz、Hxyz、Hxzz、Hyyz和Hyzz。

2階磁場(chǎng)梯度張量H中共27個(gè)參數(shù)，由于(9)式、(11)式和(13)式，且考慮對(duì)稱性，僅有7個(gè)獨(dú)立的參數(shù)，即Hxxx、Hyyy、Hxxy、Hxxz、Hyyx、Hyyz和Hxyz。

2 基于磁偶極子的2階磁場(chǎng)梯度張量縮并

定義磁偶極子的2階磁場(chǎng)梯度張量的全局模量為

(14)

(14)式即為2階磁場(chǎng)梯度張量全局縮并，將2階磁場(chǎng)梯度張量H的全部27個(gè)元素變?yōu)橐粋€(gè)標(biāo)量CH。

定義磁偶極子的2階磁場(chǎng)梯度張量局部模量CHx、CHy、CHz、CHxy、CHxz及CHyz，具體公式如下：

(15)

(16)

(17)

(18)

(19)

(20)

(15)式至(20)式為2階磁場(chǎng)梯度張量局部縮并，將2階磁場(chǎng)梯度張量H的若干元素變?yōu)闃?biāo)量CHx、CHy、CHz、CHxy、CHxz及CHyz。

根據(jù)(6)式可知，2階磁場(chǎng)梯度張量的27個(gè)參數(shù)均與磁矩的模M呈正比，與距離的5次方r5呈反比，即H∝M/r5。根據(jù)(14)式，進(jìn)一步得到全局模量CH亦與磁矩的模M呈正比，與距離的5次方r5呈反比，即CH∝M/r5。結(jié)合1階磁場(chǎng)梯度張量的全局模量與磁偶極子的磁矩的模、磁偶極子至測(cè)量系統(tǒng)的距離等之間的關(guān)系[21-22]，給出2階磁場(chǎng)梯度張量的全局模量與磁偶極子的磁矩的模、磁偶極子至測(cè)量系統(tǒng)的距離等之間的關(guān)系為

(21)

式中：kH為僅與磁偶極子的軸線及磁性目標(biāo)至測(cè)量系統(tǒng)連線夾角相關(guān)的參數(shù)。

由于H∝M/r5，通過(guò)(15)式～(20)式進(jìn)一步得到局部模量亦與磁矩的模M呈正比，與距離的5次方r5呈反比，即CHx∝M/r5、CHy∝M/r5、CHz∝M/r5、CHxy∝M/r5、CHxz∝M/r5及CHyz∝M/r5。結(jié)合1階磁場(chǎng)梯度張量的局部模量與磁偶極子磁矩的模、磁偶極子至測(cè)量系統(tǒng)的距離等之間的關(guān)系[21-22]，給出2階磁場(chǎng)梯度張量的局部模量CHx、CHy、CHz、CHxy、CHxz及CHyz與磁偶極子的磁矩的模、磁偶極子至測(cè)量系統(tǒng)的距離等之間的關(guān)系為

(22)

(23)

(24)

(25)

(26)

(27)

式中：kHx、kHy、kHz、kHxy、kHxz及kHyz為與磁偶極子的軸線和磁性目標(biāo)至測(cè)量系統(tǒng)連線的夾角及r/r二者相關(guān)的參數(shù)。

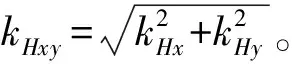
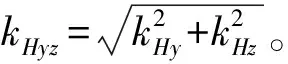
3 基于磁偶極子的2階磁場(chǎng)梯度張量縮并的仿真分析

由(2)式和(6)式，可分別計(jì)算1階和2階磁場(chǎng)梯度張量，以Bxx、Byy、Bxy和Hxxx、Hyyy、Hxyz為例比較1階磁場(chǎng)梯度張量和2階磁場(chǎng)梯度張量，計(jì)算結(jié)果如圖1～圖2所示。在圖1和圖2中，計(jì)算Bxx、Byy、Bxy和Hxxx、Hyyy、Hxyz時(shí)，為比較二者的三維空間分布規(guī)律，取M=1.0 A·m2，r=|r|=1.0 m。由于1階和2階磁場(chǎng)梯度張量均與磁矩的模M呈正比的線性關(guān)系，當(dāng)磁矩的模取其他值時(shí)，對(duì)關(guān)于1階和2階磁場(chǎng)梯度張量比較得出的結(jié)論沒有影響；對(duì)于后續(xù)1階和2階磁場(chǎng)梯度張量的全局模量及相關(guān)參數(shù)的空間分布、相關(guān)參數(shù)具體取值的公式，以及1階和2階磁場(chǎng)梯度張量的全局模量與距離的關(guān)系比較得出來(lái)的結(jié)論，同樣適用于磁矩的模取其他值的情況。

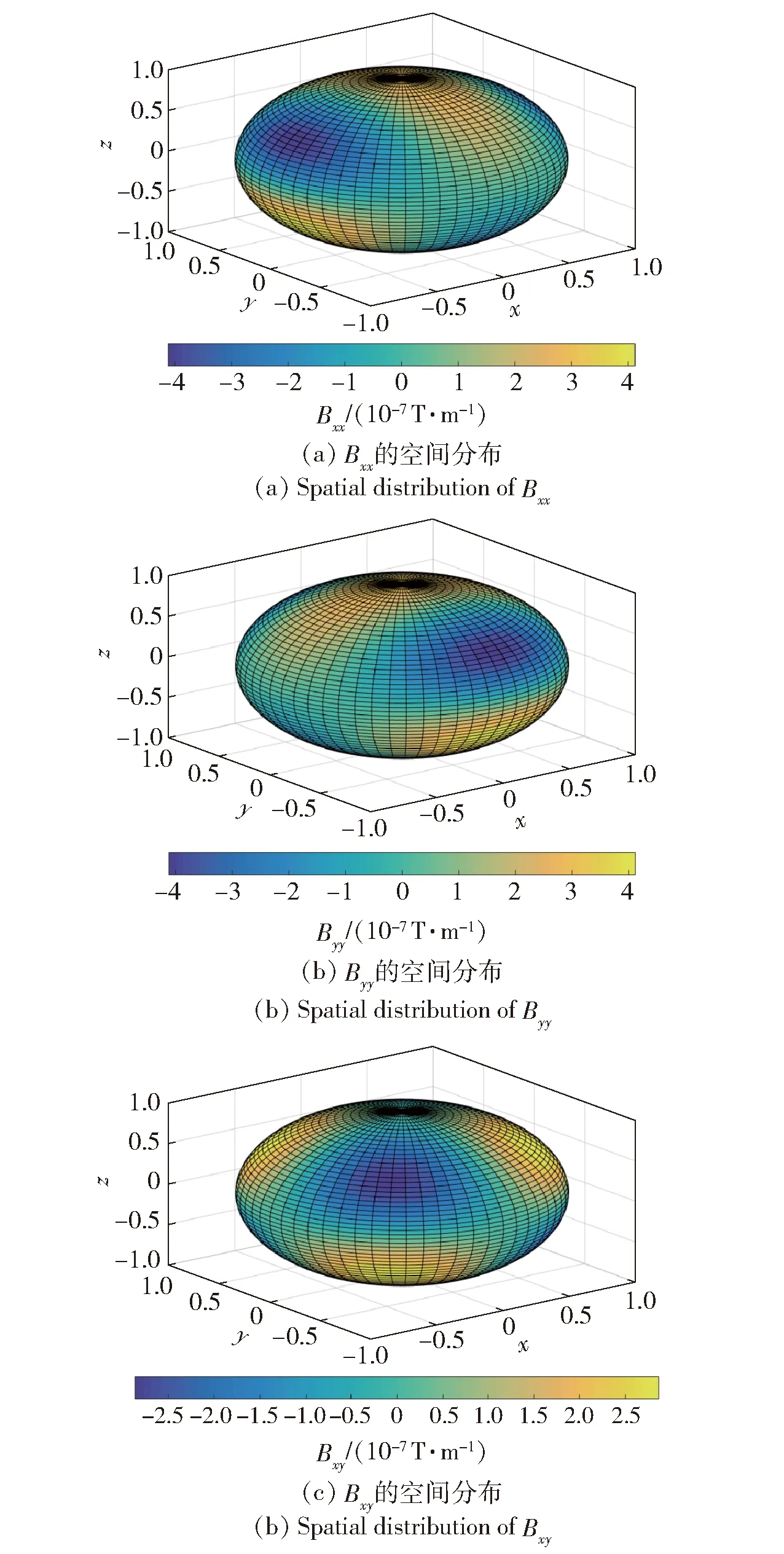
圖1 1階磁場(chǎng)梯度的三維空間分布Fig.1 3D spatial distribution of first-order magnetic gradient

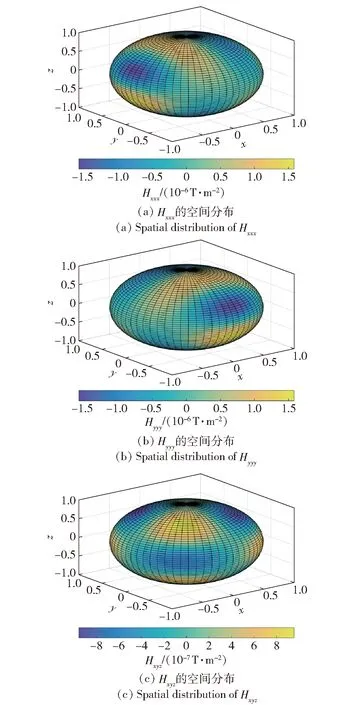
圖2 2階磁場(chǎng)梯度的三維空間分布Fig.2 3D spatial distribution of second-order magnetic gradient

由圖1和圖2可得，1階磁場(chǎng)梯度Bxx、Byy和Bxy的范圍分別為±4.13×10-7T/m、±4.13×10-7T/m和±2.88×10-7T/m；2階磁場(chǎng)梯度Hxxx、Hyyy和Hxyz的范圍分別為±1.58×10-6T/m2、±1.58×10-6T/m2和±9.64×10-7T/m2。在M=1.0 A·m2、r=|r|=1.0 m的情況下，Hxxx、Hyyy和Hxyz的絕對(duì)值最大值為Bxx、Byy和Bxy的絕對(duì)值最大值的3.35～3.83倍。

由(4)式和(14)式分別計(jì)算1階和2階磁場(chǎng)梯度張量的全局模量，即CG和CH，如圖3～圖4所示。在計(jì)算CG和CH時(shí)，取M=1.0 A·m2，r=|r|=1.0 m。

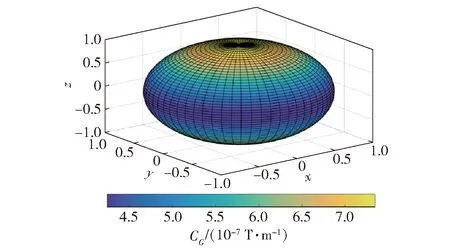
圖3 1階磁場(chǎng)梯度張量的全局模量CG的 三維空間分布Fig.3 3D spatial distribution of first-order magnetic gradient’s modulus CG

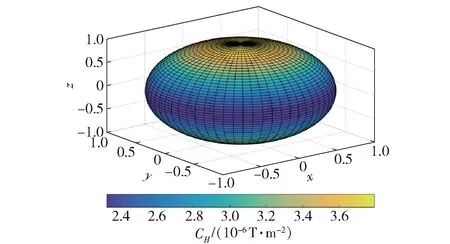
圖4 2階磁場(chǎng)梯度張量的全局模量CH的三維空間分布Fig.4 3D spatial distribution of second-order magnetic gradient’s modulus CH

由圖3和圖4可知，2階磁場(chǎng)梯度張量的全局模量CH與1階磁場(chǎng)梯度張量的全局模量CG極值分布相同：當(dāng)?=0°時(shí)(cos ?=m·r/(Mr)，表示磁偶極子的軸線與磁性目標(biāo)至測(cè)量系統(tǒng)連線夾角)，CH與CG取最大值；當(dāng)?=90°時(shí)，CH與CG取最小值。

1階磁場(chǎng)梯度張量的全局模量CG的范圍為4.242 6×10-7～7.348 5×10-7T/m；2階磁場(chǎng)梯度張量的全局模量CH的范圍為23.238×10-7～37.947×10-7T/m2。在M=1.0 A·m2，r=|r|=1.0 m的情況下，CH最大值為CG最大值的5.16～5.48倍，其倍數(shù)大于磁場(chǎng)梯度張量(3.35～3.83倍)。

由(6)式、(14)式和(21)式，可計(jì)算kH值，其三維空間分布規(guī)律如圖5所示，部分?jǐn)?shù)值見表1。在計(jì)算kH時(shí)，取M=1.0 A·m2，r=|r|=1.0 m。

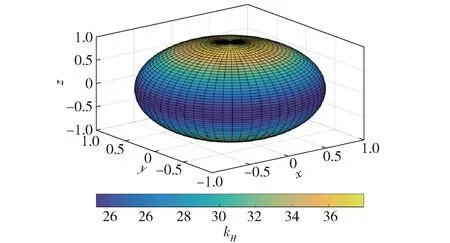
圖5 kH值的三維空間分布Fig.5 3D spatial distribution of parameter kH

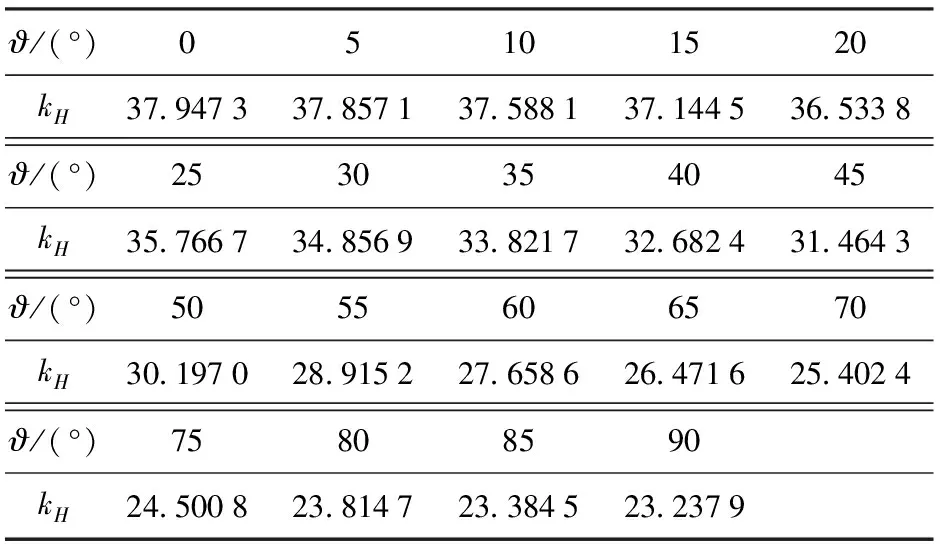
表1 kH值的理論反演值

由圖4和圖5可知，kH的三維空間分布規(guī)律與全局模量CH相同。同時(shí)，由表1可知，kH與距離r無(wú)關(guān)，只與?有關(guān)。?=0°時(shí)kH取最大值37.947 3；?=90°時(shí)kH取最小值為23.237 9。

將kH值與角度?之間進(jìn)行擬合，則擬合公式為

kH=37.973 7-0.003 695?2+2.315 1×10-7?4

(28)

當(dāng)90°≤?≤180°時(shí)，參數(shù)kH的取值與0°≤?≤90°對(duì)應(yīng)的取值對(duì)稱。

kH的理論值分布曲線與擬合公式計(jì)算值的比較如圖6所示。

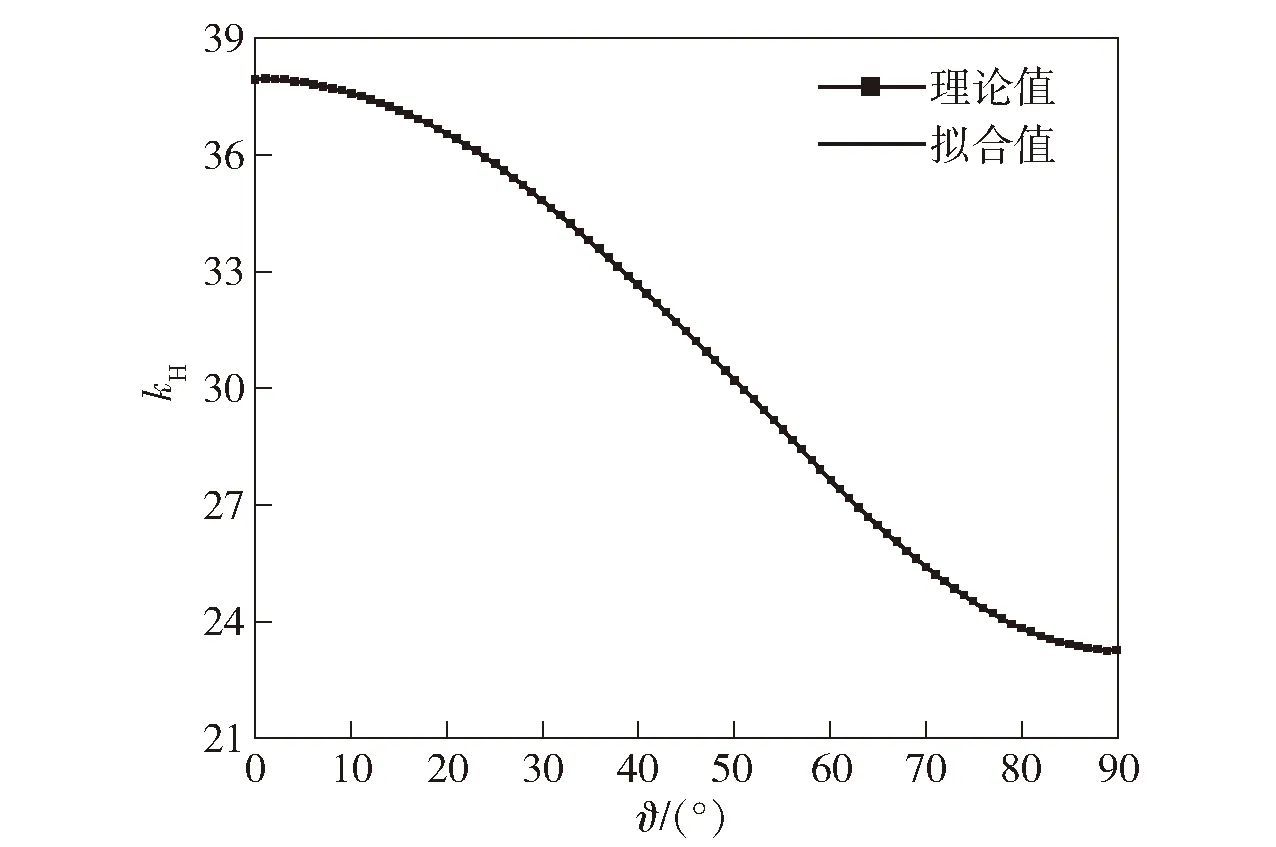
圖6 kH值的擬合Fig. 6 Fitting curve of parameter kH

由圖6可得：kH的理論值與擬合公式(28)式的計(jì)算值高度一致；理論反演值與擬合公式計(jì)算值誤差的最大值為0.028 31，均值為0.016 88，標(biāo)準(zhǔn)差為0.008 256。

2階磁場(chǎng)梯度張量的局部模量CHx、CHy、CHz、CHxy、CHxz、CHyz與M、r及?有關(guān)，在特殊情況下，當(dāng)磁偶極子軸線與坐標(biāo)軸的某個(gè)軸相同時(shí)，例如為z軸時(shí)，則CHz和CHxy僅與M、|r|及?相關(guān)，顯然在磁場(chǎng)梯度張量定位時(shí)更為簡(jiǎn)便快速，因此，后面分析磁偶極子軸線方向?yàn)閦軸方向時(shí)CHz和CHxy及參數(shù)kHz和kHxy，其三維空間分布規(guī)律如圖7～圖10所示。參數(shù)kHz和kHxy的具體取值如表2所示。

圖7 CHxy的空間分布Fig.7 Spatial distribution of parameter CHxy

圖8 kHxy值的空間分布Fig.8 Spatial distribution of parameter kHxy

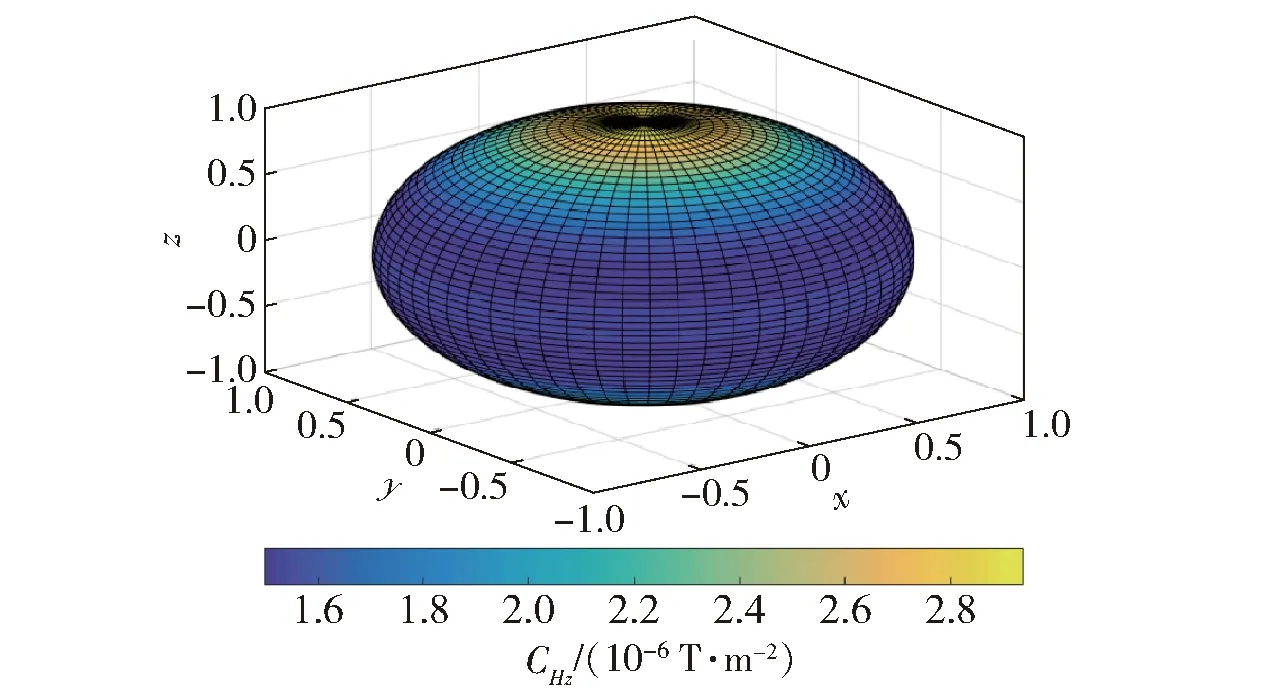
圖9 CHz的空間分布Fig.9 Spatial distribution of parameter CHz

圖10 kHz值的空間分布Fig.10 Spatial distribution of parameter kHz

由圖7可知，對(duì)于相等距離r的測(cè)量位置：在0°≤?≤90°時(shí)，CHxy先增大、后減少；在?=35°時(shí)CHxy取最大值；在?=90°時(shí)CHxy取最小值。由圖8可知，kHxy的三維分布趨勢(shì)與CHxy一致。同時(shí)，由表2可知，kHxy和r無(wú)關(guān)，只和?有關(guān)。在?=0°時(shí)kHxy為24.000 0；在?=35°時(shí)kHxy取最大值25.806 7；在?=90°時(shí)kHxy取最小值17.492 9。

由圖9可得，對(duì)于相等距離r的測(cè)量位置：在0°≤?≤90°時(shí)CHz先減少后增加；在?=0°時(shí)Cz取最大值；在?=71°時(shí)CHz取最小值。通過(guò)圖10可知，kHz的三維分布與CHz相同。同時(shí)，由表2可知，kHz和r無(wú)關(guān)，只和?有關(guān)。在?=0°時(shí)，kHz取最大值29.3939；在?=71°時(shí)，kHz取最小值14.967 3；在?=90°時(shí)，kHz為15.297 1。

kHxy和kHz與r無(wú)關(guān)，只與?相關(guān)，kHxy和kHz可表示為

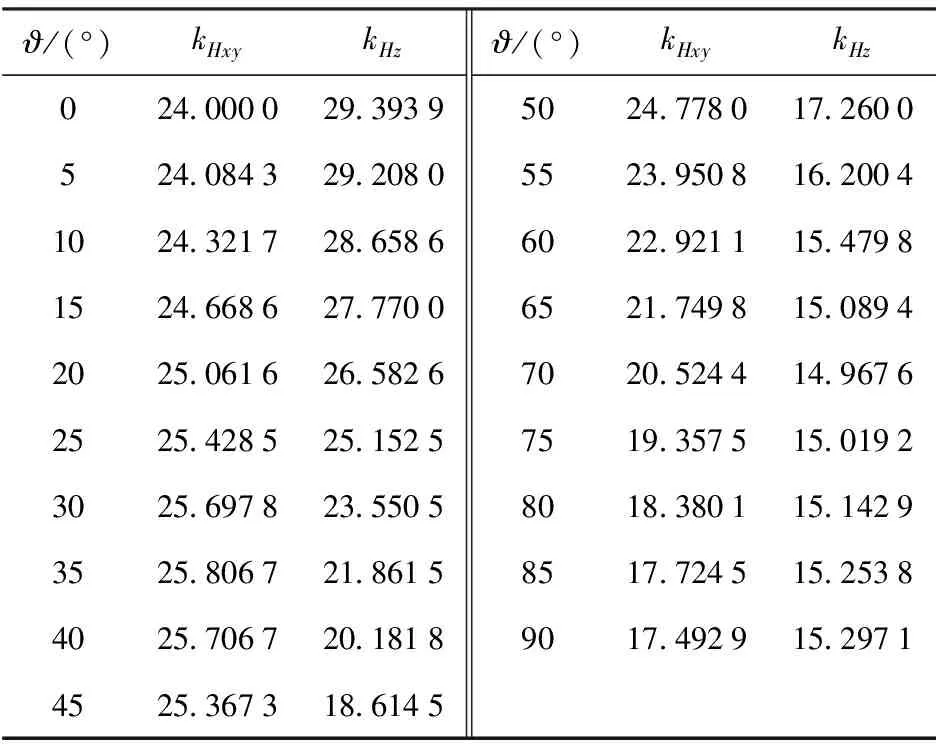
表2 kHxy和kHz值的理論反演值Table 2 Theoretical inversion value of parameterskHxy and kHz

kHxy=24.146 6-6.160 4×10-2?+9.320 3× 10-3?2-2.218 8×10-4?3+1.297 4×10-6?4

(29)

(30)

參數(shù)kHxy和kHz的理論分布曲線及其和擬合公式(29)式、(30)式的計(jì)算值的比較如圖11和圖12所示。

圖11 kHxy值的擬合Fig.11 Fitting curve of parameter kHxy

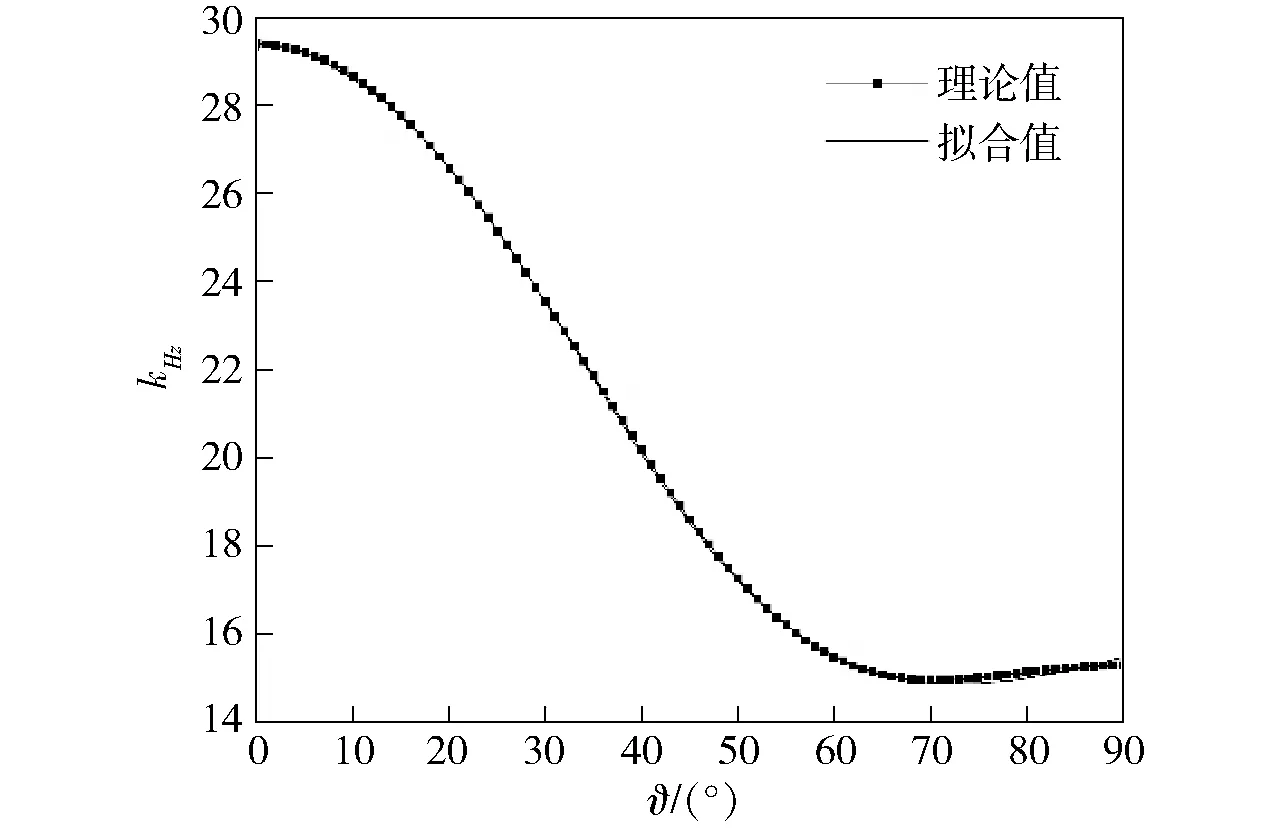
圖12 kHz值的擬合Fig.12 Fitting curve of parameter kHz

由圖11可得，kHxy的理論反演值與擬合公式(29)式計(jì)算值高度吻合；理論反演值與擬合公式計(jì)算值誤差的最大值為0.146 6，均值為0.032 49，標(biāo)準(zhǔn)差為0.021 36。

由圖12可得，kHz的理論反演值與擬合公式(30)式計(jì)算值高度吻合；理論反演值與擬合值誤差的最大值為0.182 0，均值為0.050 35，標(biāo)準(zhǔn)差為0.039 69。

4 基于磁偶極子的1階和2階磁場(chǎng)梯度張量及全局模量與距離的關(guān)系

取M=1.0 A·m2，當(dāng)距離r=0.01 m、0.1 m、1 m、10 m、100 m、1 000 m時(shí)，由(2)式和(6)式，可分別計(jì)算不同距離情況下的1階和2階磁場(chǎng)梯度張量，以Bxx、Bxy和Hxxx、Hxyz為例，進(jìn)行仿真分析，給出各自的取值范圍，比較1階磁場(chǎng)梯度張量和2階磁場(chǎng)梯度張量與距離r的規(guī)律，結(jié)果如表3所示。其中比值范圍為max(|Hxxx|)/max(|Bxx|)和max(|Hxyz|)/max(|Bxy|)中取值的最大值和最小值。

表3 1階和2階磁場(chǎng)梯度張量與距離的關(guān)系Table 3 Relationship between magnetic gradient and distance

由表3可知：

1)當(dāng)距離從0.01 m增加到1 000 m時(shí)，1階磁場(chǎng)梯度Bxx的范圍從±4.13×10 T/m衰減到±4.13×10-19T/m，Bxy的范圍從±2.88×10 T/m衰減到±2.88×10-19T/m，Bxx和Bxy與距離的四次方呈反比，與(2)式中1階磁場(chǎng)梯度和距離的關(guān)系一致；2階磁場(chǎng)梯度張量Hxxx的范圍從±1.58×104T/m2衰減到±1.58×10-21T/m2，Hxyz的范圍從±9.64×103T/m2衰減到±9.64×10-22T/m2，Hxxx和Hxyz與距離的5次方呈反比，與(6)式中2階磁場(chǎng)梯度和距離的關(guān)系一致。

2)當(dāng)距離為0.01 m、0.1 m、1 m時(shí)，2階磁場(chǎng)梯度張量的絕對(duì)值最大值大于1階磁場(chǎng)梯度張量，且在距離越小時(shí)，2階與1階磁場(chǎng)梯度張量的比值越大；即在較小距離時(shí)，2階磁場(chǎng)梯度張量比1階在數(shù)值上更大更敏感；距離越小，2階磁場(chǎng)梯度張量越敏感。

3)當(dāng)距離為10 m、100 m、1 000 m時(shí)，2階磁場(chǎng)梯度張量的絕對(duì)值最大值小于1階磁場(chǎng)梯度張量，且距離越大，2階與1階磁場(chǎng)梯度張量的比值越小；即在距離較大時(shí)，2階磁場(chǎng)梯度張量比1階在數(shù)值上更小且衰減更快，相對(duì)而言，此時(shí)1階磁場(chǎng)梯度張量更敏感。

4)由上所述可知，在磁性物體的探測(cè)過(guò)程中，如距離較遠(yuǎn)，則采用1階磁場(chǎng)梯度張量更靈敏，如距離較近，則采用2階磁場(chǎng)梯度張量更靈敏；在磁測(cè)過(guò)程為了消除干擾磁場(chǎng)，當(dāng)干擾磁場(chǎng)較遠(yuǎn)時(shí)，采用2階磁場(chǎng)梯度張量更易消除干擾磁場(chǎng)，當(dāng)干擾磁場(chǎng)較近時(shí)，采用1階磁場(chǎng)梯度張量更易消除干擾磁場(chǎng)。在實(shí)際應(yīng)用時(shí)，可結(jié)合1階和2階磁場(chǎng)梯度張量進(jìn)行使用，有助于同時(shí)提高靈敏度和消除地磁場(chǎng)等干擾磁場(chǎng)。

取M=1.0 A·m2，當(dāng)距離r=0.01 m、0.1 m、1 m，10 m、100 m、1 000 m時(shí)，由(4)式和(14)式進(jìn)行仿真分析，分別計(jì)算不同距離情況下的1階和2階磁場(chǎng)梯度張量的全局模量，即CG和CH，給出CG和CH的取值范圍，比較1階和2階磁場(chǎng)梯度張量的全局模量與距離的關(guān)系，結(jié)果如表4所示。

由表4可知：

1)當(dāng)距離從0.01 m增加到1 000 m時(shí)，1階磁場(chǎng)梯度張量的全局模量CG的范圍從4.242 6×10～7.348 5×10 T/m衰減到4.242 6×10-19～7.348 5×10-19T/m，與距離的4次方呈反比，與(5)式中1階磁場(chǎng)梯度張量的全局模量和距離的關(guān)系一致；2階磁場(chǎng)梯度張量的全局模量CH的范圍從2.323 8×104～3.794 7×104T/m2衰減到2.323 8×10-21～3.794 7×10-21T/m2，與距離的5次方呈反比，與(21)式中2階磁場(chǎng)梯度張量的全局模量和距離的關(guān)系一致。

表4 1階和2階磁場(chǎng)梯度張量的全局模量與距離的關(guān)系Table 4 Relationship between magnetic gradient’s full modulus and distance

2)當(dāng)距離為0.01 m、0.1 m、1 m時(shí)，2階磁場(chǎng)梯度張量的全局模量的最大值大于1階磁場(chǎng)梯度張量的全局模量，且在距離越小時(shí)，2階與1階磁場(chǎng)梯度張量的全局模量的比值越大；即在較小距離時(shí)，2階磁場(chǎng)梯度張量全局模量比1階在數(shù)值上更大更敏感；距離越小，2階磁場(chǎng)梯度張量的全局模量越敏感。

3)當(dāng)r=10 m、100 m、1 000 m時(shí)，2階磁場(chǎng)梯度張量的全局模量最大值小于1階，且距離越大，2階與1階磁場(chǎng)梯度張量的全局模量的比值越小；即在r較大時(shí)，2階磁場(chǎng)梯度張量的全局模量在數(shù)值上比1階更小且衰減更快，相對(duì)而言，此時(shí)1階磁場(chǎng)梯度張量的全局模量更敏感。

4)由上述可知，在磁性物體的探測(cè)過(guò)程中，當(dāng)距離較遠(yuǎn)時(shí)，采用1階磁場(chǎng)梯度張量的全局模量更靈敏，當(dāng)距離較近時(shí)，采用2階磁場(chǎng)梯度張量的全局模量更靈敏；在磁測(cè)過(guò)程為了消除干擾磁場(chǎng)，當(dāng)干擾磁場(chǎng)較遠(yuǎn)時(shí)，采用2階磁場(chǎng)梯度張量的全局模量更易消除干擾磁場(chǎng)，當(dāng)干擾磁場(chǎng)較近時(shí)，采用1階磁場(chǎng)梯度張量的全局模量更易消除干擾磁場(chǎng)。在實(shí)際應(yīng)用時(shí)，可結(jié)合1階和2階磁場(chǎng)梯度張量的全局模量進(jìn)行使用，有助于同時(shí)提高靈敏度和消除地磁場(chǎng)等干擾磁場(chǎng)。

由(5)式和(21)式，可得到1階和2階磁場(chǎng)梯度張量的全局模量的比值與距離的關(guān)系式，即

(31)

由(31)式可知，對(duì)于同一個(gè)測(cè)點(diǎn)(由角度?和距離r確定)，若1階和2階磁場(chǎng)梯度張量的全局模量相等，則相應(yīng)的距離r取值如下：

(32)

由于參數(shù)kH和kG均僅與?有關(guān)，則1階和2階磁場(chǎng)梯度張量的全局模量相等時(shí)對(duì)應(yīng)的距離也僅與?相關(guān)，如表5所示。

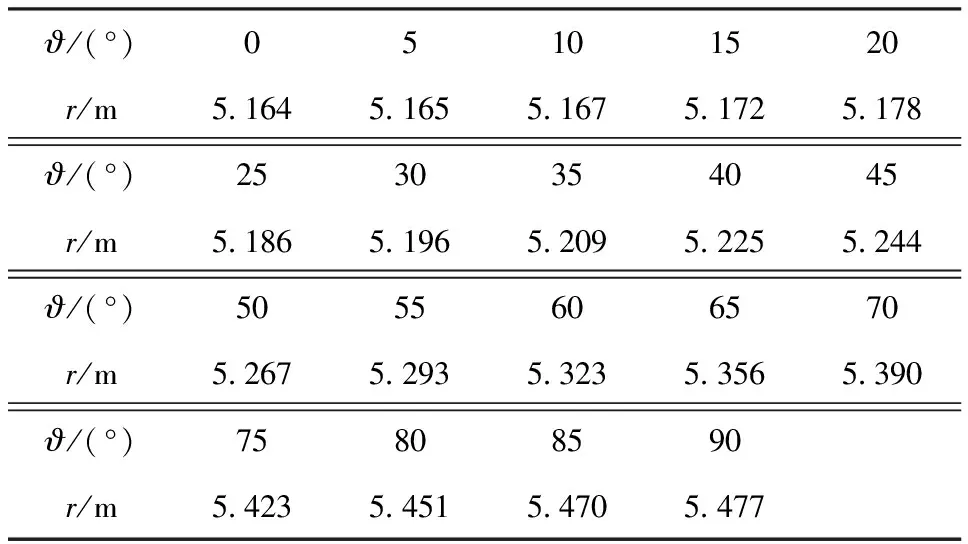
表5 1階和2階磁場(chǎng)梯度張量的全局模量 相等時(shí)的距離Table 5 Relationship between angle and distance when CG=CH

由表5可得，如1階和2階磁場(chǎng)梯度張量的全局模量相等，則距離在5.164～5.477 m之間，具體數(shù)值僅與?相關(guān)。

由(32)式可知，當(dāng)距離rCG，即2階磁場(chǎng)梯度張量的全局模量大于1階，距離越小，CH/CG的值越大；當(dāng)距離r>kH/kG時(shí)，CHCG，2階磁場(chǎng)梯度張量的全局模量小于1階，距離越大，CH/CG的值越小。此規(guī)律與表4中的數(shù)據(jù)一致。

5 結(jié)論

1)本文提出了基于磁偶極子的2階磁場(chǎng)梯度張量縮并方法，探討了全局模量、局部模量及參數(shù)kH的三維空間分布，給出了相關(guān)參數(shù)kH、kHxy和kHz的近似計(jì)算公式，比較了1階和2階磁場(chǎng)梯度張量及全局模量與距離的關(guān)系。

2)0°≤?≤90°時(shí)，全局模量CH及參數(shù)kH隨著?增大而減小，在?=0°時(shí)最大，在?=90°時(shí)最小。0°≤?≤90°時(shí)，局部模量CHxy和kHxy隨?先增加后減少，當(dāng)?=35°時(shí)最大，當(dāng)?=90°時(shí)最小；局部模量CHz和kHz隨?先減少、后增加，當(dāng)?=71°時(shí)最小，當(dāng)?=0°時(shí)最大。

3)給出了2階磁場(chǎng)梯度張量的全局模量和局部模量的計(jì)算中相關(guān)參數(shù)kH、kHxy和kHz的近似計(jì)算公式，且理論反演值和擬合值吻合度極高。

4)在距離較近時(shí)，2階磁場(chǎng)梯度張量更敏感，2階磁場(chǎng)梯度張量及全局模量的取值大于1階；在距離較遠(yuǎn)時(shí)，1階磁場(chǎng)梯度張量更敏感，2階磁場(chǎng)梯度張量及全局模量的取值小于1階。在實(shí)際應(yīng)用時(shí)，可結(jié)合1階和2階磁場(chǎng)梯度張量的全局模量進(jìn)行使用。

5)鑒于2階磁場(chǎng)梯度張量在磁場(chǎng)定位方面的應(yīng)用價(jià)值，2階磁場(chǎng)梯度張量縮并方法有必要進(jìn)一步的試驗(yàn)驗(yàn)證。