基于傳感布置優化的履帶車輛振動測試系統

楊書儀， 廖力力， 覃凌云， 戴巨川， 陳哲吾， 何興云， 仝寧可

(1.湖南科技大學 機電工程學院， 湖南 湘潭 411201； 2.長沙金維信息技術有限公司， 湖南 長沙 410006；3.江麓機電集團有限公司， 湖南 湘潭 411201；4.蘇州韋博試驗儀器有限公司， 江蘇 蘇州 215000)

0 引言

履帶車輛由于具有接地比壓小、牽引附著能力強等優點，在現代農業、軍事、建筑等領域發揮著重要作用[1-2]。履帶車輛行走系統通常由主動輪、負重輪、誘導輪、履帶、托帶輪、履帶張緊機構等組成。履帶車輛在野地、陡坡以及壕溝等工況下工作時，地面不平所帶來的振動、沖擊會通過履帶傳遞到負重輪、懸掛系統、車身以及其他操作機構，這不僅會加速履帶車輛主要零部件疲勞失效，還會降低車輛配備儀器使用精度和可靠性，甚至對駕乘人員身心健康產生嚴重影響[3-5]。履帶車輛擁有良好的抗振性能是其使用壽命長、運行可靠、乘坐舒適度高的重要保障指標之一。開展履帶車輛振動特性測試是掌握其抗振性能影響因素的重要途徑，也可為履帶車輛抗振性結構設計、輕量化設計提供實踐指導。

目前，在大尺寸結構件振動測試中，因傳感器布置冗余或者布置數量過少而導致測試結果誤差大等問題，引起了眾多學者的關注。傳感布置優化本質是一種組合優化，即將有限數量傳感器分配至結構自由度節點上。通常采用遺傳算法、粒子群優化(PSO)算法以及深度學習等智能優化算法可以有效提高尋優精度，更好地解決工程實際問題。文獻[6-7]采用不同的智能算法對傳感器布局進行研究。文獻[8]針對復雜地形下的多傳感器多目標優化部署問題，提出基于多目標局部變異- 自適應量子PSO算法。文獻[9-10]分別提出了基于Kalman多輸入估計的最優傳感器布置方法和基于頻率響應函數的傳感器布置方法。文獻[11]利用PSO算法解決齒輪箱故障檢測中傳感器優化布置問題，并通過試驗驗證了方法的可行性。文獻[12]提出一種定位算法對不均勻網絡中傳感布置進行優化。文獻[13]提出一種多目標傳感器布置優化方法，可有效處理傳感器對空間動態載荷的測量。

本文擬以履帶車輛為研究對象，提出一種慣性權值遞減協同學習因子呈指數函數特征的非線性調整策略，并從尋優精度和穩定性方面與標準PSO算法、文獻[14]和文獻[15]所提算法進行對比分析，結合履帶車輛有限元模態分析，開展振動加速度傳感布置優化計算，采用MATLAB和LabView混合編程方式，設計集傳感布置優化于一體的履帶車輛振動測試系統。

1 履帶車輛振動傳感布置優化理論

履帶車輛車身質心垂向加速度和繞質心軸俯仰角加速度通過半車模型可以描述，因而本文擬采用履帶車輛半車為研究對象，運用動力學微分方程描述其振動狀態為

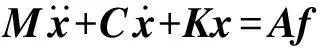
(1)

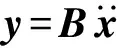
(2)

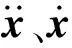
系統特征方程為

Kφi=λiMφi，i=1，2，…，n

(3)

式中：λi和φi分別為第i階模態的特征值和振型向量。由系統特征方程計算出有限元處理后的結構總模態矩陣：φ=[φ1，φ2，…，φn]。通過優化B、Φ的取值即優化傳感器布置，可使得傳感器測量響應中各階目標模態相互獨立并盡可能獲取較多的模態信息[16]。

本文采用模態置性準則(MAC)[17]作為傳感布置優化準則，MAC矩陣元素計算公式為

(4)

式中：φi和φj分別為第i階和第j階模態向量。

2 履帶車輛振動傳感布置優化算法設計

2.1 PSO-IWLF算法

本文采用一種慣性權值遞減協同學習因子呈指數函數特征的非線性調整策略，將這種改進算法稱為慣性權值協同學習因子非線性動態調整PSO(PSO-IWLF)算法[18]。(5)式為PSO-IWLF算法中調整策略數學表達式。

(5)

式中：ω為慣性權值；ωmax和ωmin分別為慣性權值最大值和最小值；c1和c2為時變學習因子；a和b為常數；t表示當前迭代次數；T表示最大迭代次數。

在履帶車輛振動傳感布置優化計算中，設粒子種群規模為N，搜索空間為D，xi=(xi1，xi2，…，xiD)T可作為粒子的當前位置，即優化問題的一個解。粒子的搜索速度可用vi=(vi1，vi2，…，viD)T表示，粒子歷史最優位置可用pbesti=(pi1，pi2，…，piD)T表示，種群歷史最優位置可用gbest=(g1，g2，…，gD)T表示。其位置和速度更新公式如下：

(6)

(7)

式中：t表示當前優化計算過程的迭代次數。

2.2 PSO-IWLF算法性能測試及分析

選取標準PSO算法、慣性權值遞減策略PSO(記為PSO-ω)算法[14]、學習因子非線性變化策略的PSO(記為PSO-c)算法[15]以及PSO-IWLF算法4個典型測試函數進行對比分析。

針對4個測試函數均設計4組對比測試，在各組測試中，設置粒子種群規模N為25，最大迭代次數T為500，搜索空間D為10，表1為算法參數設置。

表1 算法參數設置Table 1 Algorithm parameter settings

4個典型測試函數表示形式如下：

1)Rastrigin函數：

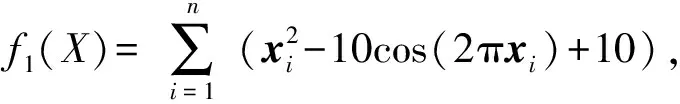
(8)

2)Sphere函數：

(9)

3)Rosenbrock函數：

(10)

4)Griewank函數：

(11)

4種典型測試函數尋優計算60次，得到各策略最優值變化曲線如圖1所示，平均解、最差解以及最優解如表2所示。

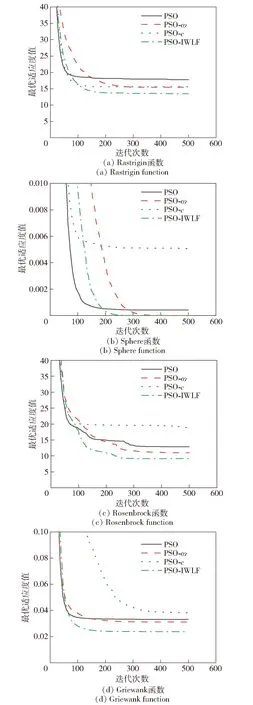
圖1 4種測試函數的平均最優值變化曲線Fig.1 Curves of average optimal value changes of four test functions

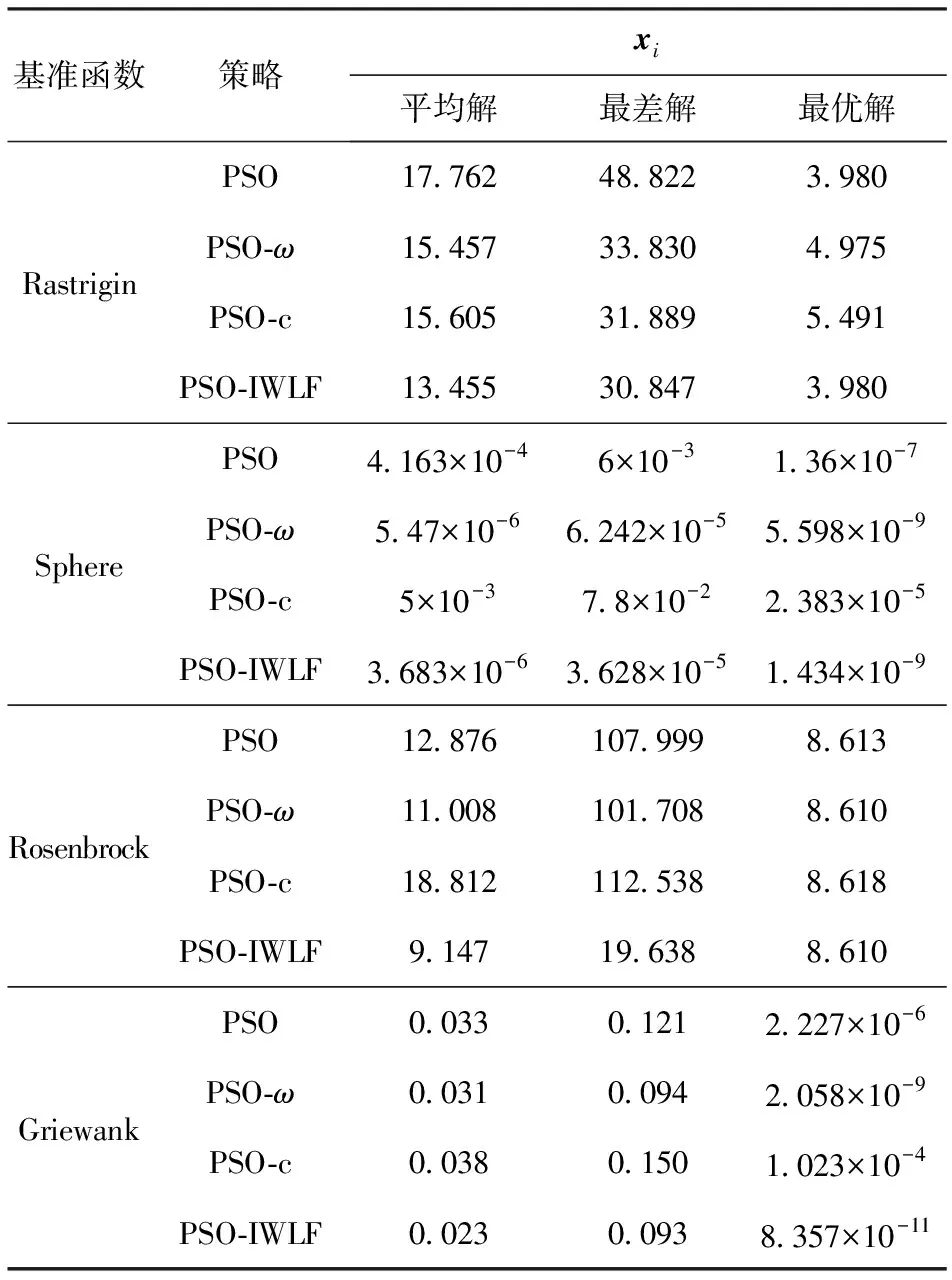
表2 4種策略測試結果比較

從表2中可知，在4種典型函數測試中，PSO-IWLF算法在尋優精度和穩定性上都優于標準PSO算法、PSO-ω算法以及PSO-c算法，這表明PSO-IWLF算法有效提高了求解收斂精度、穩定性。

3 車身振動測試傳感布置優化

3.1 履帶半車有限元模態分析

履帶車輛振動測試試驗傳感布置優化實現過程如圖2所示。

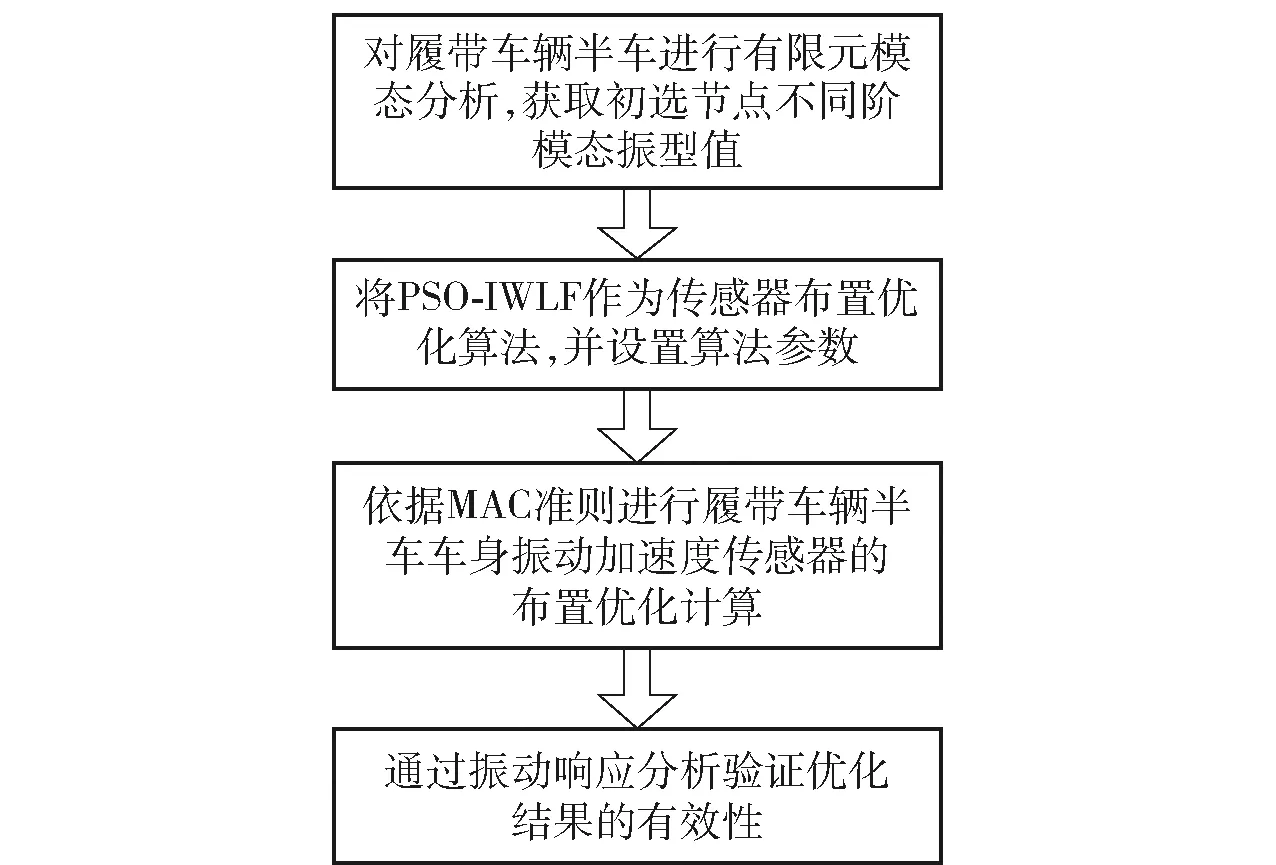
圖2 傳感布置優化實現過程Fig.2 Realization process of sensor layout optimization

圖3所示為履帶車輛半車有限元模型，將履帶車輛沿z軸直線運動以及繞x軸旋轉運動自由度釋放，其余自由度約束，作為模型邊界條件并計算各階模態振型。有限元分析模態振型圖如圖4所示。

圖3 履帶車輛半車有限元模型Fig.3 Finite element model of the semi-tracked vehicle

圖4 履帶車輛半車有限元分析模態振型Fig.4 Finite element analysis of modal shape of the semi-tracked vehicle

3.2 初選點的選擇與編碼

車身初選測點如圖5所示。

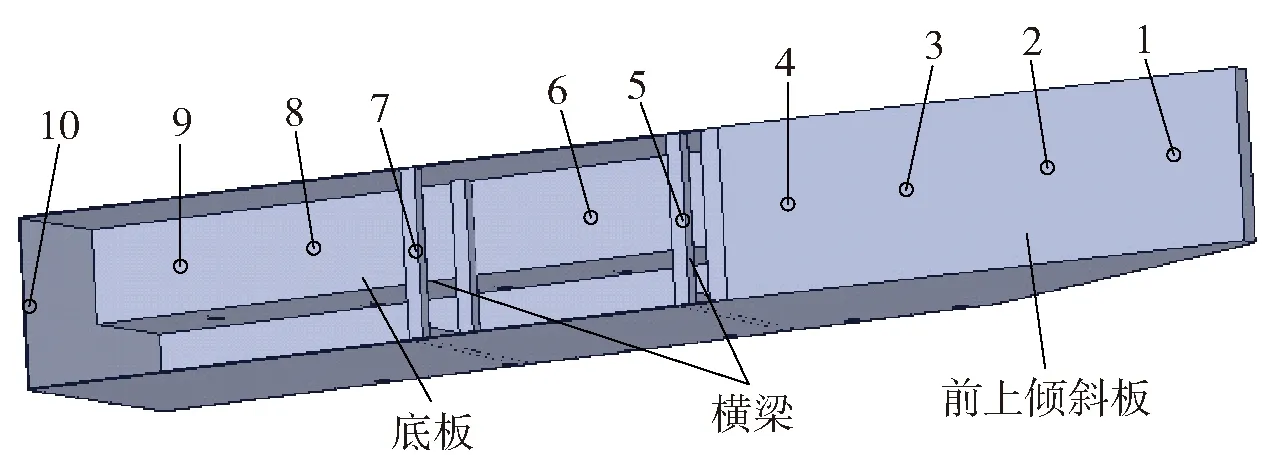
圖5 車身初選測點布置Fig.5 Primary test point arrangement of vehicle body

初選測點的節點編碼及節點各階模態頻率所對應的模態振型計算結果如表3所示。

履帶車輛半車屬于大尺寸空間結構，其模態具有密集、低頻特性。由表3可知，節點30 480的7階與8階模態振型數值就較為接近。履帶車輛半車模態的這一特性對后續傳感布置優化算法沒有直接影響，本文不予考慮。

3.3 PSO-IWLF算法實現

PSO-IWLF算法中相應參數設置如下：粒子種群規模N設為10；搜索空間D根據所選初選測點數及振動傳感器布置數目設置范圍為[1，10]；最大迭代次數T為100；傳感器布置位置的邊界值xmax=10、xmin=1；算法參數調整策略中，取常數a=1.7，常數b=2.5。 慣性權值和學習因子變化曲線如圖6所示。

由圖6可知，隨著迭代次數的增加，時變學習因子c1呈非線性遞減，而c2呈非線性遞增。在該策略中，當0≤迭代次數<200時，ω調整較慢，因此c1、c2變化較慢，這時全局搜索能力較強，粒子可以遍歷整個搜索空間；當200≤迭代次數<500時，ω和c1、c2均變化較快，使得各粒子向全局最優位置快速收斂。

3.4 優化計算結果及分析

以MACij的最大值作為傳感布置優化的適應度函數，對傳感器布置位置和數目進行雙重尋優。圖7為最優適應度值隨傳感器布置數目的變化曲線。

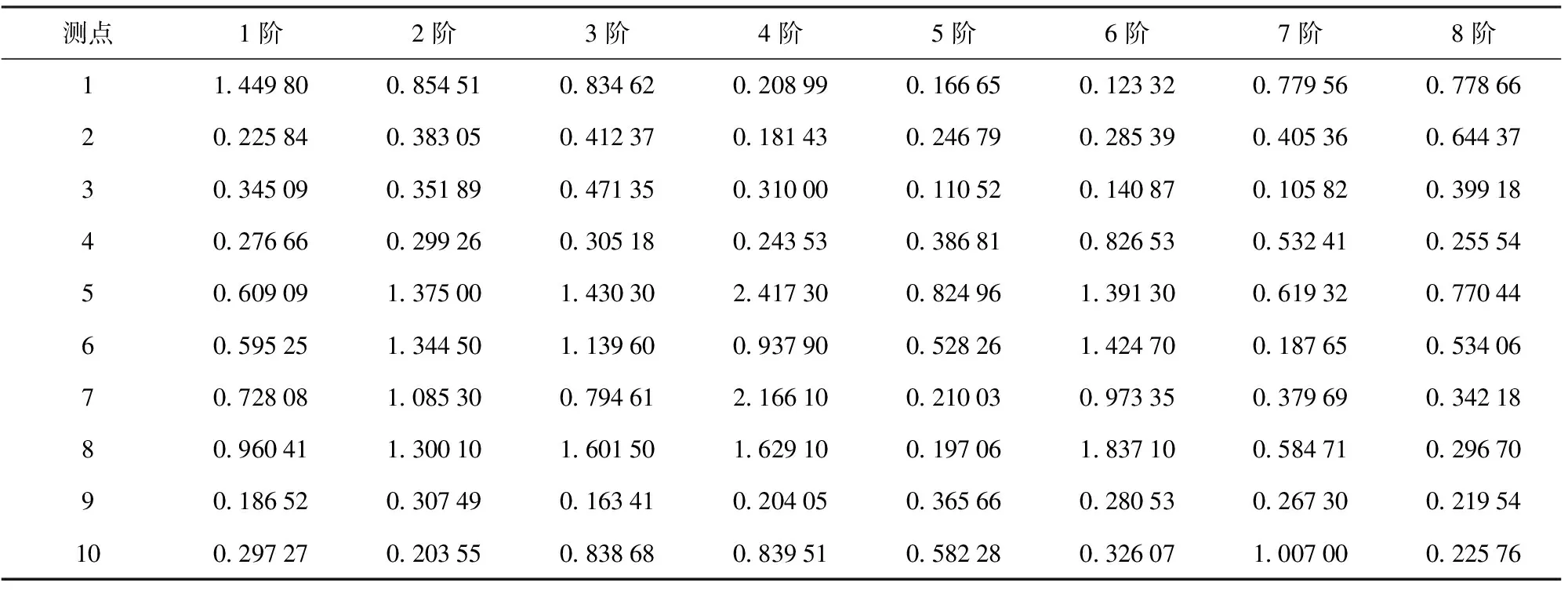
表3 初選測點8階模態振型Table 3 8th-order modal shape of primary selected measuring points mm

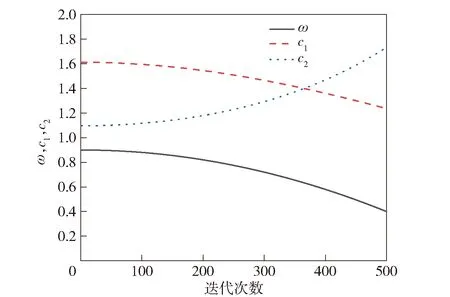
圖6 慣性權值和學習因子變化曲線Fig.6 Variation curve of inertia weight and learning factor

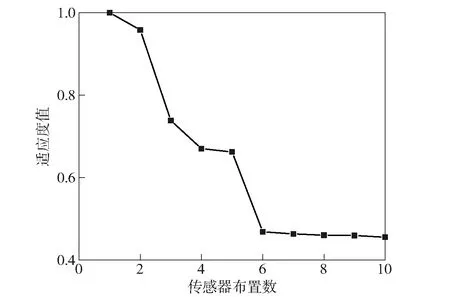
圖7 最優適應度值變化曲線Fig.7 Variation curve of optimum fitness value

不同傳感器布置數目所對應的最優適應度和傳感器布置位置如表4所示。

從圖7和表4可知，最優適應度值隨傳感器布置數目增加而逐漸減少，當布置數目為6時，適應度 值較小且后續隨著傳感器布置數目的增加，適應度值變化幅度很小，對測點布置效果提升貢獻較小。考慮綜合成本和測試效果，布置6個傳感器，位置為[2，3，4，5，9，10]較為合理。

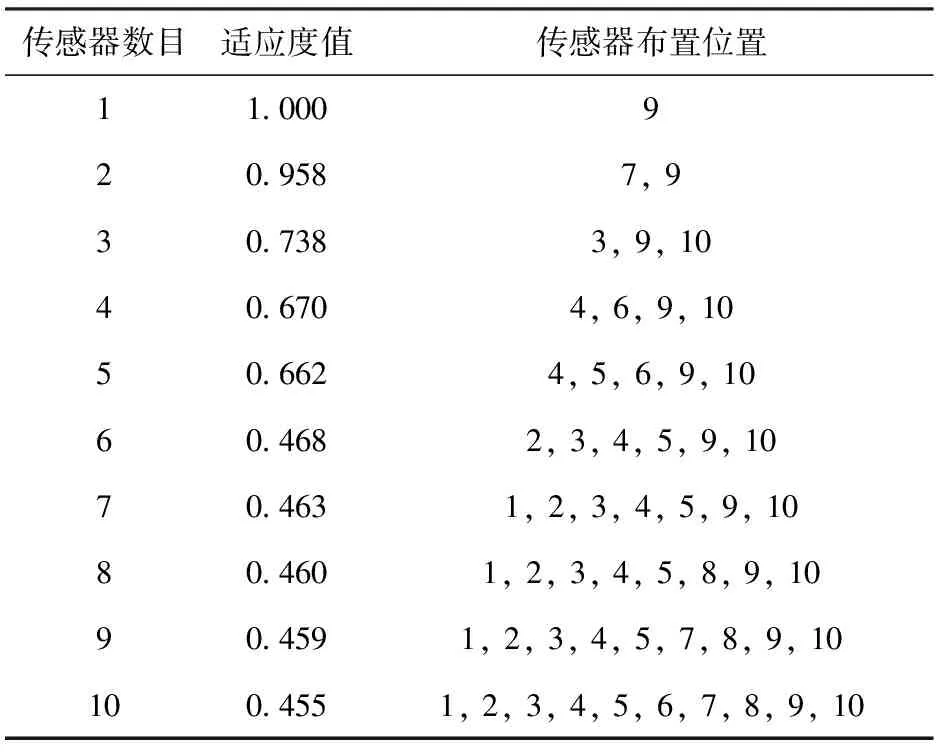
表4 傳感器布置數目和位置Table 4 Number and position of sensors

4 履帶車輛振動測試系統設計

本文采用MATLAB軟件和LabView軟件混合編程方式[19-20]，設計集PSO-IWLF優化算法于一體的履帶車輛振動測試系統，為傳感器布點提供依據。履帶車輛振動測試系統結構框圖如圖8所示。

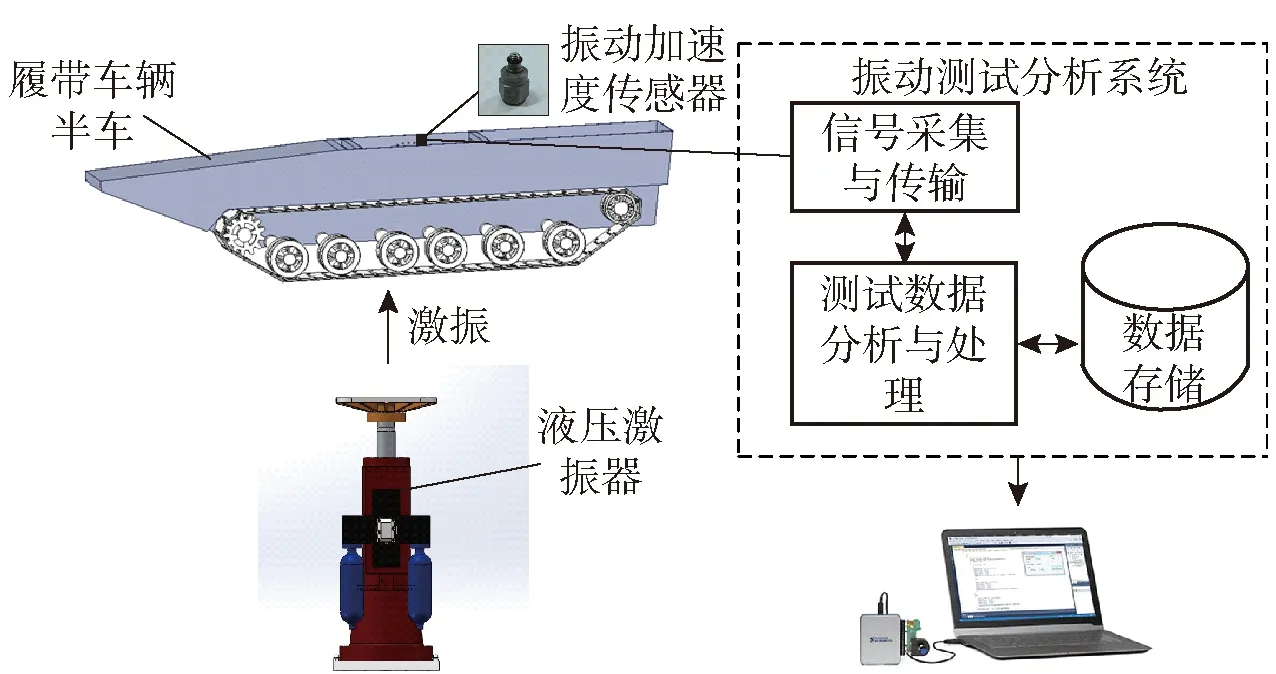
圖8 振動測試系統結構框圖Fig.8 Block diagram of vibration test system structure

履帶車輛振動測試系統硬件部分包括丹麥B&K公司生產的4514型壓電式加速度傳感器和美國NI公司生產的USB-6366型數據采集卡等。表5、表6分別為加速度傳感器和數據采集卡的主要性能指標。

履帶車輛振動測試系統的功能主要分為兩部 分：第1部分為實驗前對振動傳感器布置優化計算和信號采集硬件參數設置；第2部分是對試驗數據進行存儲和讀取，并對試驗數據進行分析和處理。系統可完成對信號的時域分析、頻域分析以及時頻分析。履帶車輛振動測試系統軟件功能框圖如圖9所示。

表5 加速度傳感器主要性能指標Table 5 Main performance indicators of acceleration sensor

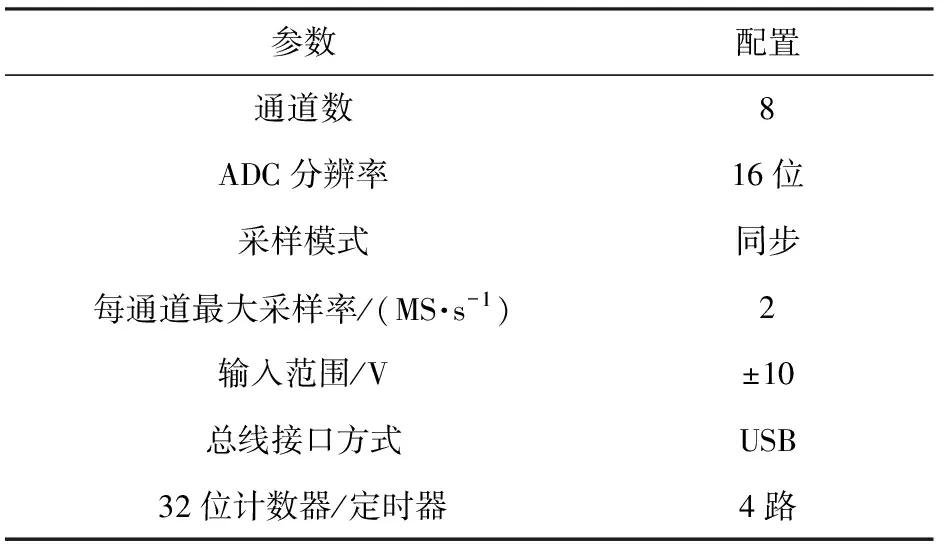
表6 數據采集卡主要參數指標Table 6 Main parameters of data acquisition card

圖9 履帶車輛振動測試系統軟件功能框圖Fig.9 Software function block diagram of tracked vehicle vibration test system

數據采集界面如圖10所示，將該測試軟件命名為LabMat。

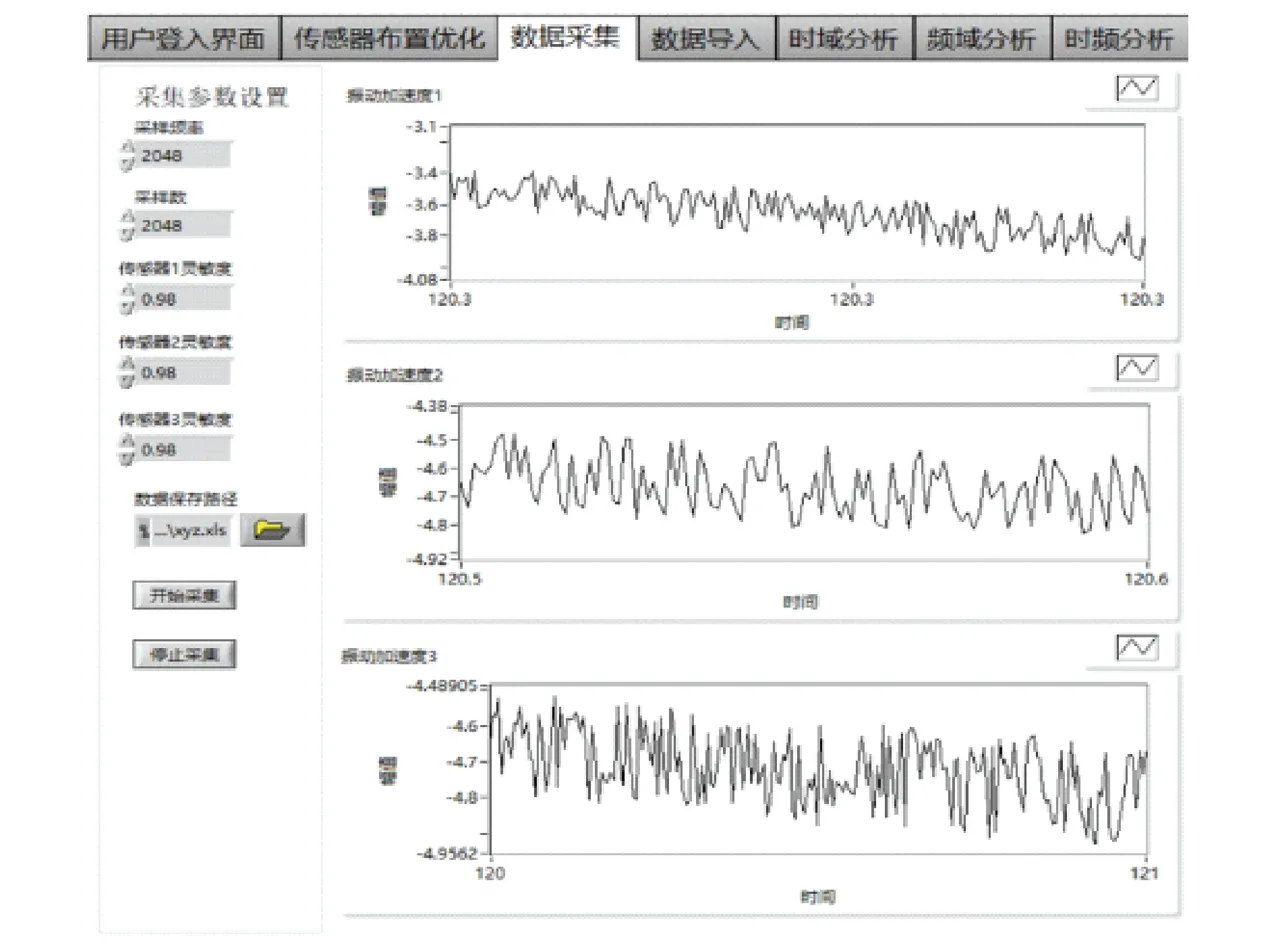
圖10 履帶車輛振動測試軟件界面Fig.10 Tracked vehicle vibration test software interface

傳感布置優化程序框圖如圖11所示，其中傳感布置優化功能模塊的參數設置主要有粒子種群規模N、搜索空間D、履帶車輛振動測試傳感布置優化計算所設置的最大迭代次數T以及傳感布置位置的邊界值xmax、xmin等。

圖11 傳感布置優化程序框圖Fig.11 Block diagram of sensor arrangement optimization program

5 履帶車輛振動測試試驗及分析

5.1 履帶車輛半車振動試驗臺

履帶車輛半車振動試驗裝置如圖12所示，測試試驗被試對象為履帶車輛半車模型，包括履帶、負重輪、懸掛裝置和車身等部件。履帶車輛半車振動試驗臺激振系統是由6組液壓激振器組成的陣列。

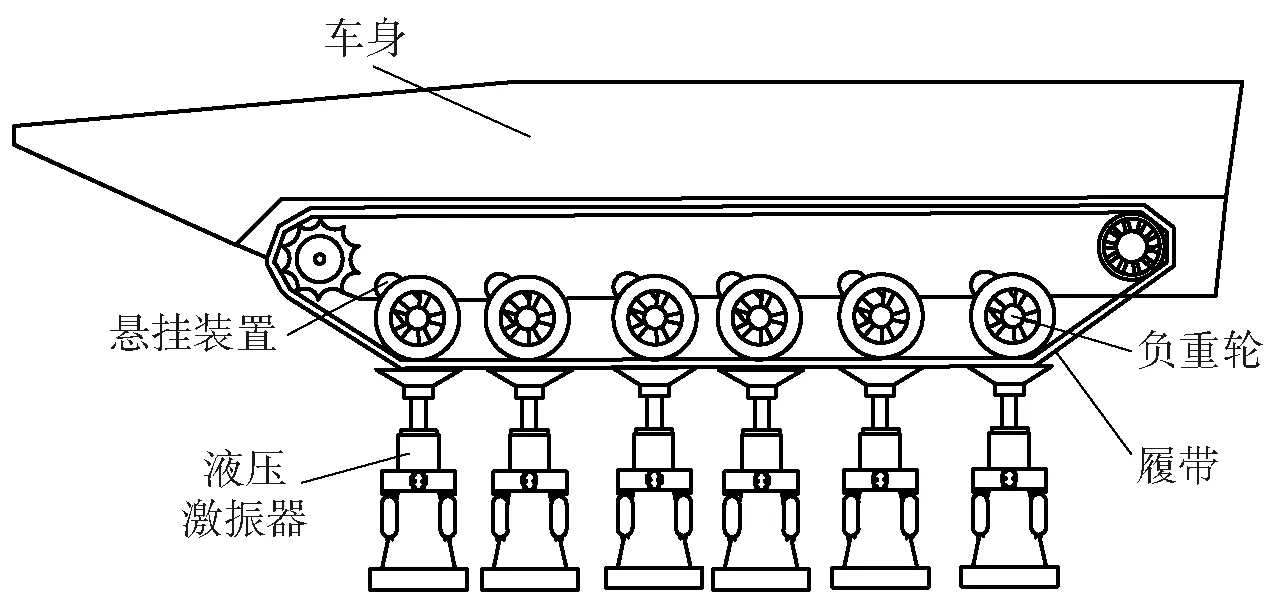
圖12 履帶車輛振動試驗裝置示意圖Fig.12 Schematic diagram of tracked vehicle vibration test devices

5.2 車身振動測試傳感布置優化試驗驗證

依據圖5所示的傳感器布置方案，在履帶車輛實驗半車上布置10個4514型單軸振動加速度傳感器，采樣頻率為8 192 Hz，現場測試系統如圖13(a) 所示。圖13(b)為傳感器安裝圖，其中旋轉移動復合機構安裝在反力墻上，用于半車車身約束，實現車身質心垂直運動和車身繞質心軸俯仰運動。

圖13 履帶車輛半車振動測試現場Fig.13 Semi-vehicle vibration test site for tracked vehicles

在0～50 Hz隨機路譜激勵下，計算10個測點60 s內加速度均方根值、峰值，結果如表7所示。

均方根值描述激勵對響應的有效性，均方根值越大，可表征在激勵下，測點的響應越大[21]。綜合兩方面響應效果，響應強烈的6個測點為[1，2，3，4，9，10]。與PSO-IWLF算法優化結果[2，3，4，5，9，10]相比，測點1和測點5位置存在偏差，這主要是本算例中優化算法目標相對單一所致，其余5個測點二者完全相同。這表明了PSO-IWLF算法的有效性和可靠性。

5.3 車身振動測試試驗

以履帶車輛行進速度15 km/h的戈壁路面譜、砂石路面譜、鋪面路面譜以及起伏路面譜信號作為激勵，用本文開發的LabMat振動測試軟件和商用LabGenius振動測試軟件同時測得車體振動加速度信號如圖14～圖17所示。

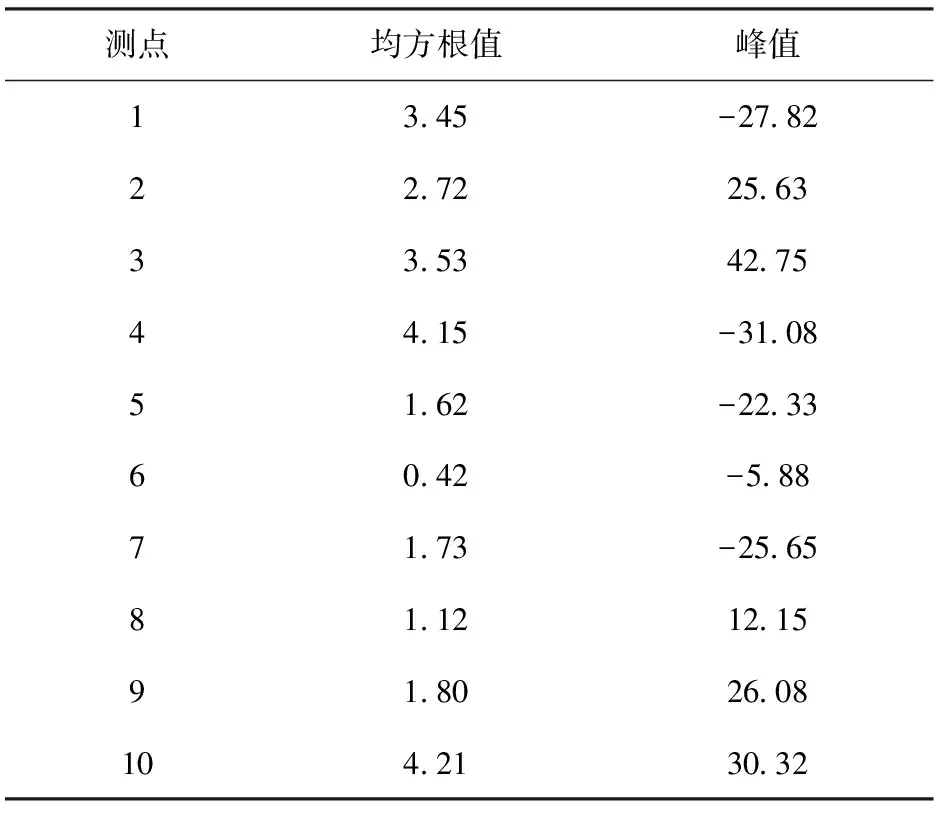
表7 加速度均方根值與峰值Table 7 Root mean square value and peak value of acceleration m/s2

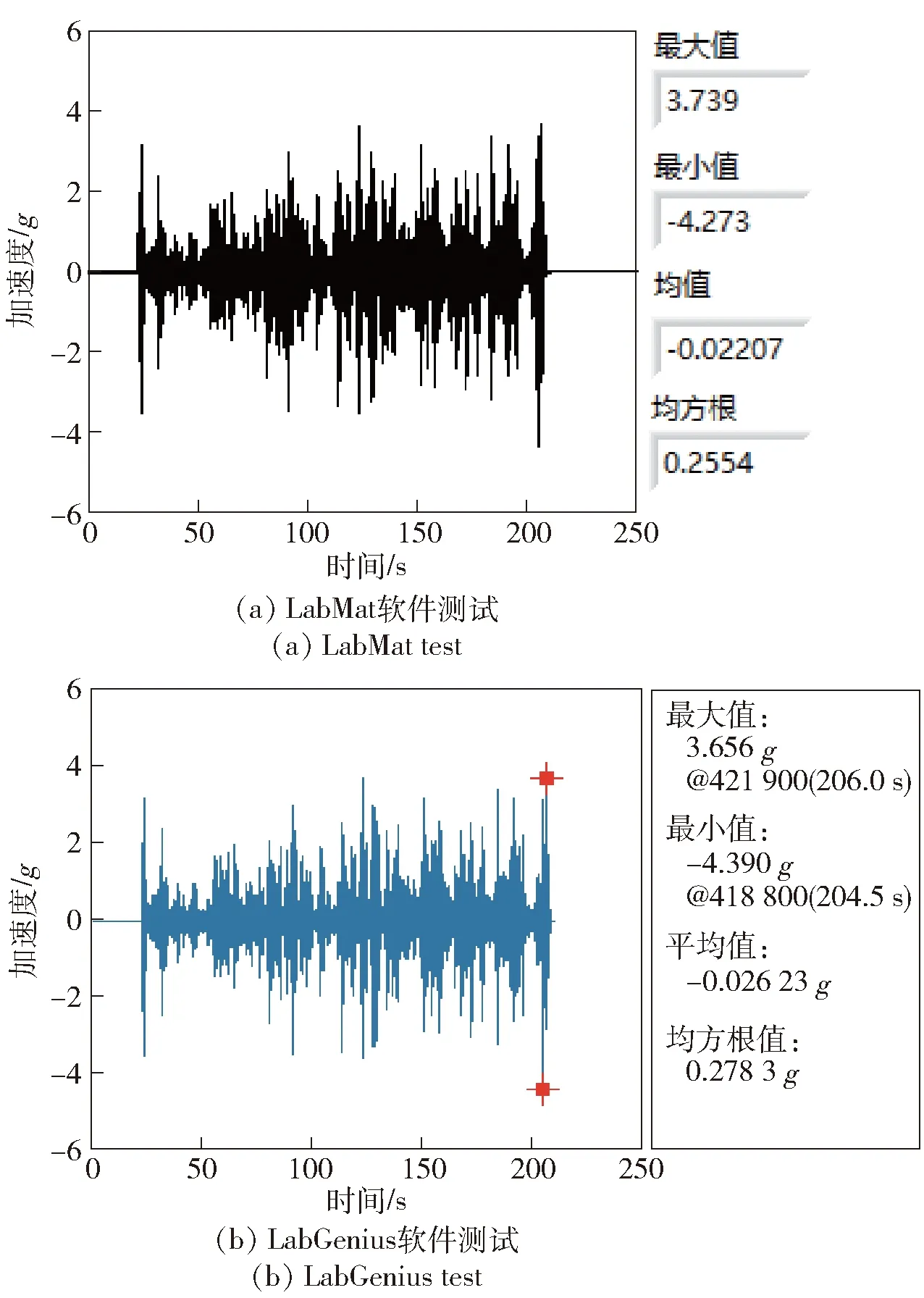
圖14 戈壁路面譜下的車身振動加速度信號Fig.14 Vehicle body vibration acceleration signal under gobi road spectrum

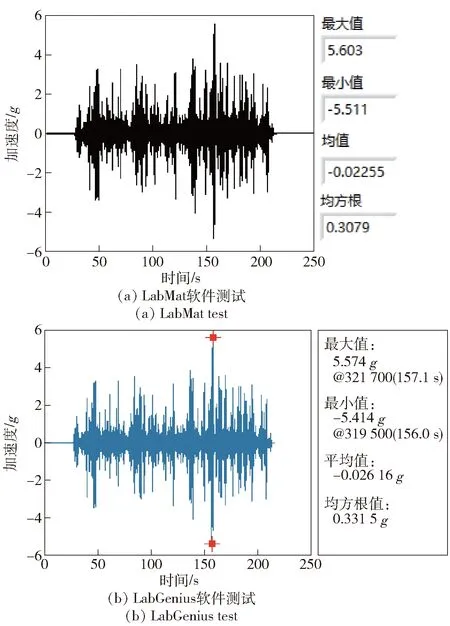
圖15 砂石路面譜下的車身振動加速度信號Fig.15 Vehicle body vibration acceleration signal under gravel road spectrum

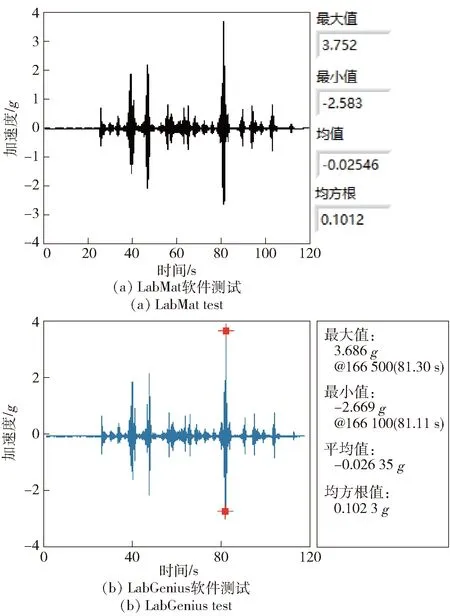
圖16 鋪面路面譜下的車身振動加速度信號Fig.16 Vehicle body vibration acceleration signal under paved road spectrum

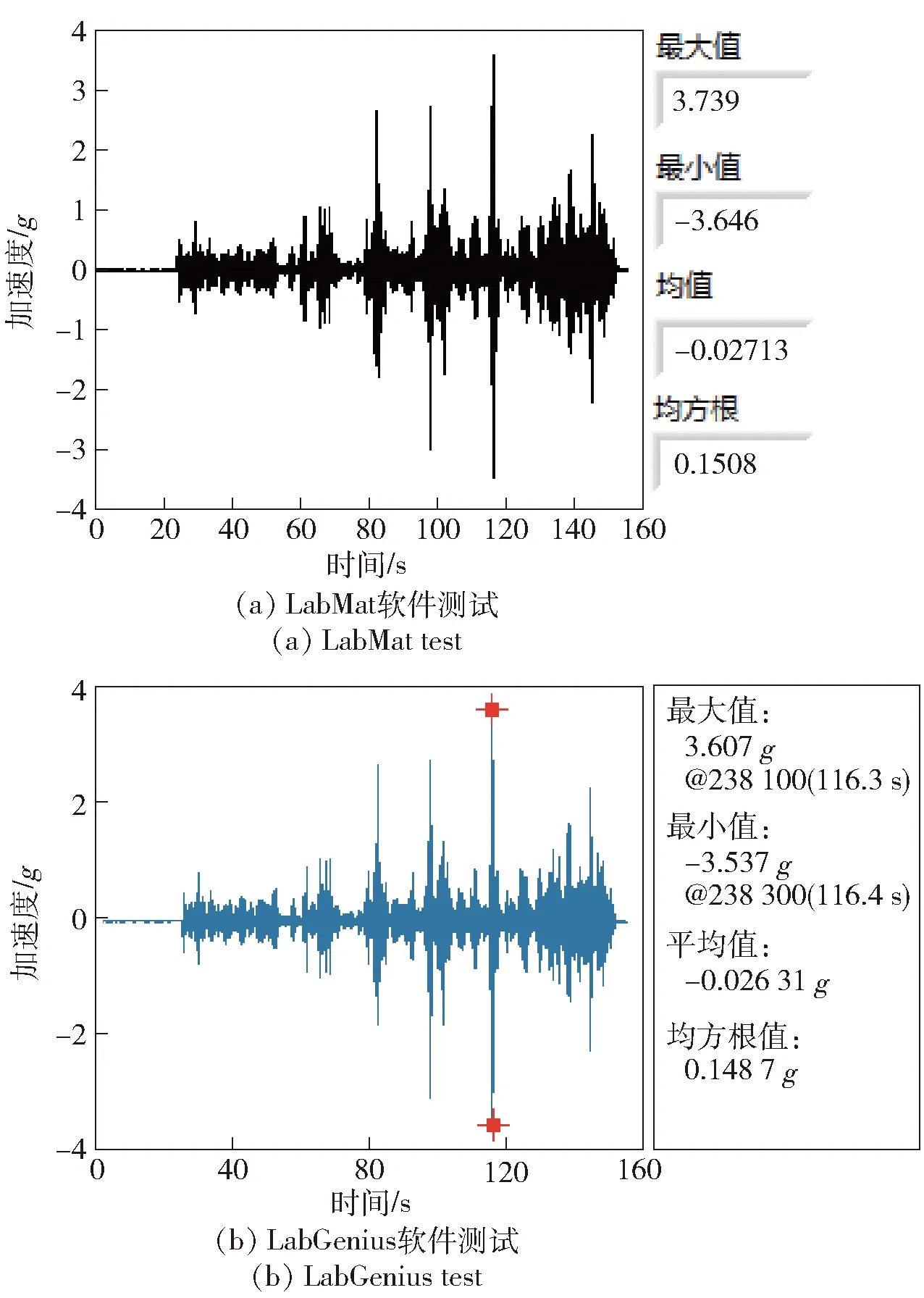
圖17 起伏路面譜下的車身振動加速度信號Fig.17 Vehicle body vibration acceleration signal under undulating road spectrum

由圖14～圖17可知，履帶車輛車身振動加速度最大值、最小值、均值、均方根值基本一致，誤差小于1%，這表明了LabMat測試軟件采集功能模塊的可行性。

6 結論

本文針對履帶車輛振動測試傳感布置多維優化問題，提出一種PSO-IWLF算法，結合履帶車輛有限元模態分析，開展振動加速度傳感布置優化及振動測試系統研究。得出以下主要結論：

1)在4種典型函數測試中，PSO-IWLF算法相對于標準PSO算法、PSO-ω算法、PSO-c算法具有更高的求解收斂精度和穩定性。

2)車身振動加速度傳感器布置優化計算，與各測點振動響應實測結果基本一致，有效解決了車輛振動測試中傳感布置冗余問題，具有良好的實踐應用價值。

3)嵌入PSO-IWLF優化算法的履帶車輛振動測試系統LabMat界面友好、操作方便，與商用振動測試系統LabGenius相比，測試結論表明LabMat振動測試系統具有良好的可行性，適應了傳感布置優化的發展需求，為大型結構件振動測試提供新的解決方案。