2016年中科大自主招生不等式試題的證明、變式及推廣

劉遠桃 陳明萬 唐明坤

(貴州師范大學數學科學學院 550025)

1 試題呈現

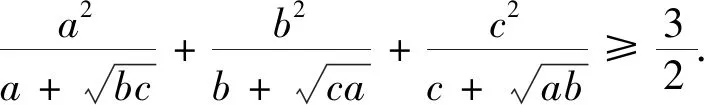
分析 此題是一道分式不等式證明題，每個分式項的分子都是一個二次單項式，分母都是二項式，由整式和根式組成，各分式項結構對稱.由此入手，想到將根式化為整式，再利用基本不等式、權方和不等式等進行證明．

2 試題證明

證法1由基本不等式和權方和不等式得

評注此證法利用基本不等式將式子中各項的分母代數式有理化，再利用權方和不等式進行放縮，湊出(a+b+c)項，將條件式a+b+c=3代入得到證明．

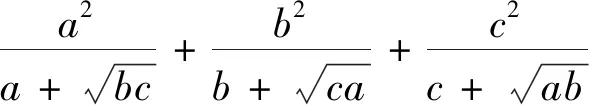
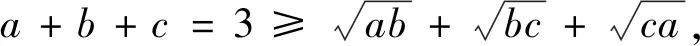
評注此證法利用柯西不等式將原不等式進行轉化，得到一個新的放縮不等式，再利用三元基本不等式求出放縮值的最小值，從而得到證明．

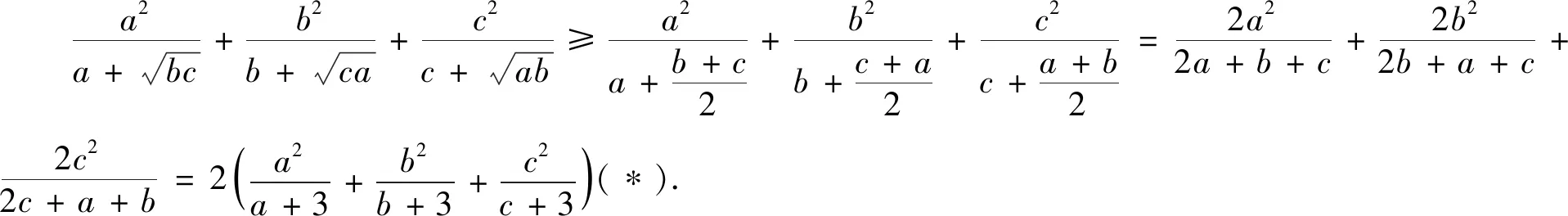
評注此證法利用基本不等式將式子中各項的分母代數式有理化，結合條件式a+b+c=3將原不等式進行放縮，再利用函數凹凸性和琴生不等式求出放縮后的最小值，從而得到證明．

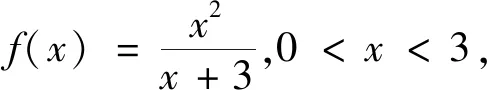
評注此證法利用基本不等式將式子中各項的分母代數式有理化，結合條件式a+b+c=3將原不等式進行放縮，再利用切線不等式求出放縮后的最小值，從而得到證明．

3 試題變式

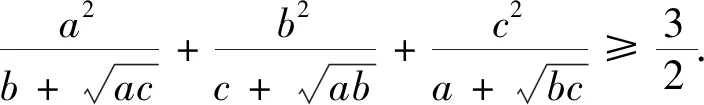
在一般情況下，對多數藥品貯藏溫度要求在2℃以上時，溫度愈低，對保管愈有利。在使用和保存藥品前務必看清藥品說明書，以免有差錯。

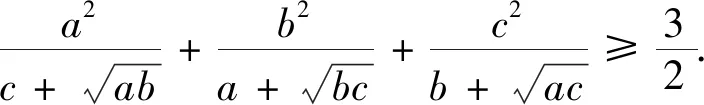
分析變式1與變式2是將試題中不等式的分母代數式進行整體輪換得到的，其證明方法與試題的證明完全一致．此外，還可以對試題中不等式的分母代數式進行部……