具有Cuntz半群消去律的C*-代數(shù)

范慶齋， 安璐

(上海海事大學文理學院，上海 201306)

0 引 言

ELLIOTT分類綱領(lǐng)指出，一類順從的C*-代數(shù)可以按照K-理論、跡態(tài)空間及K-理論與跡態(tài)空間的配對(通常稱為ELLIOTT不變量)進行分類。有許多重要的C*-代數(shù)類已經(jīng)按照ELLIOTT不變量進行了分類，例如ELLIOTT等[1-2]對于單的有單位元的AH代數(shù)的分類。受到ELLIOTT等[1-2]關(guān)于單的AH代數(shù)分類的啟發(fā)，LIN[3]提出跡拓撲秩不超過k的C*-代數(shù)，在這類C*-代數(shù)中，去掉了C*-代數(shù)的歸納極限結(jié)構(gòu)，提出了一種新的C*-代數(shù)構(gòu)造方法。這種新的結(jié)構(gòu)，事實上就是由一類好C*-代數(shù)類通過跡逼近之后得到的C*-代數(shù)類。這種構(gòu)造一方面去掉了歸納極限的結(jié)構(gòu)，更容易驗證某些C*-代數(shù)在這類C*-代數(shù)中，另一方面大大簡化了分類定理中的唯一性定理。GONG等[4]對于單的順從有單位元關(guān)于Jiang-Su代數(shù)穩(wěn)定滿足UTC條件的C*-代數(shù)給出了分類。事實上他們證明了這樣的C*-代數(shù)是在一類稱為廣義跡拓撲秩不超過1的C*-代數(shù)張量上的一個UHF代數(shù)。

廣義跡拓撲秩不超過1的C*-代數(shù)具有好的正則性質(zhì)。正則性質(zhì)在C*-代數(shù)分類中起關(guān)鍵的核心作用。正則性質(zhì)一般是指關(guān)于Jiang-Su代數(shù)Z穩(wěn)定、有限核維數(shù)、Cuntz半群的某些性質(zhì)(例如Cuntz 半群的嚴格比較性質(zhì)、可除性質(zhì)等)。對于單的可分有單位元順從的C*-代數(shù)，TOMS和WINTER猜想這3類正則性質(zhì)等價。

ELLIOTT等[5]考慮了Ω類是滿足某些性質(zhì)的C*-代數(shù)，這些性質(zhì)可以遺傳到由Ω類中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)類中。例如穩(wěn)定秩一和投影的序由跡態(tài)決定等性質(zhì)。并且這些性質(zhì)對于某類C*-代數(shù)的分類起到關(guān)鍵性的作用。

FAN[6-7]考慮了Ω中某些K-群或者K-半群的性質(zhì)可以遺傳到由Ω類中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)中。FAN[8]、ELLIOTT等[9]證明了Ω中某些正則性質(zhì)可以遺傳到由Ω類中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)中。

R?RDAM等[10]提出Cuntz半群的弱消去律和投影的消去律，并證明了如果C*-代數(shù)是穩(wěn)定秩一的，則它的Cuntz半群具有弱消去律和投影的消去律。

在本文中，設(shè)Ω是一類Cuntz半群具有弱消去律的C*-代數(shù)或者Cuntz半群具有投影消去律的C*-代數(shù)，證明了Cuntz半群的弱消去律性質(zhì)或者Cuntz半群投影的消去律性質(zhì)可以遺傳到由Ω中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)類TAΩ中。作為上述結(jié)論的應(yīng)用：如果A是一個無限維有單位元單的Cuntz半群具有弱消去律性質(zhì)的C*-代數(shù)(或者Cuntz半群具有投影消去律的C*-代數(shù))，且設(shè)α:G→Aut(A)是有限群G作用在C*-代數(shù)A上并且作用具有跡Rokhlin性質(zhì)，則交叉積C*-代數(shù)C*(G,A,α)的Cuntz半群具有弱消去律性質(zhì)(或者Cuntz半群具有投影消去律)。

1 準備知識和定義

一個C*-代數(shù)A具有性質(zhì)SP，是指對于A的任意非零可傳C*-子代數(shù)，都包含一個非零投影。

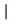
稱a與bCuntz等價(記為a～b)，滿足a?b并且b?a。記〈a〉為a的等價類。

〈a〉+〈b〉=〈a⊕b〉

序關(guān)系為

〈a〉≤〈b〉?a?b

設(shè)a和b是C*-代數(shù)A中的正元，記作[a]≤[b]，如果存在部分等距v∈A**使得對于任意的0≤c∈Her(A)，cv∈A，vv*=Pa，v*Her(a)v=Her(b)，其中Pa是a在A**中值域的投影(由[a]≤[b]可以得到aCuntz子等價于b，即a?b)。記[a]=[b]，滿足v*Her(a)v=Her(b)。假設(shè)n是一個正整數(shù)，記n[a]≤[b]，則存在n個相互垂直的正元b1,b2,…,bn∈Her(b)滿足[a]≤[bi]，i=1,2,…,n[11]。

設(shè)A是穩(wěn)定有限的C*-代數(shù)，一個正元a∈A稱為純正元，滿足a不Cuntz等價于一個投影。這等價于0不是a的譜σ(a)的聚點。

給定M∞(A)+中的正元a和ε>0，記(a-ε)+是由函數(shù)f(t)=max(t-ε,0),t∈σ(a)通過函數(shù)演算對應(yīng)C*(a)中的元，由函數(shù)演算知道((a-ε1)+-ε2)+=(a-(ε1+ε2))+。

定理1.1A是一個有單位元穩(wěn)定有限的C*-代數(shù)。

(1)設(shè)a,b∈A,任意的ε>0，如果||a-b||<ε，則存在A中一個壓縮的元d使得(a-ε)+=dbd*。

(2)a是一個純正元，對于任意的δ>0，任意的一個非負函數(shù)f∈C0(0,1]滿足||f||=1，且在(δ/2,1)上f=0，在(0,δ/2)上f>0，則f(a)≠0，且(a-δ)++f(a)?a。

(3)下列等價：①a?b；②對于任意的ε>0，(a-ε)+?b；③對于任意的ε>0，存在δ>0，使得(a-ε)+?(b-δ)+。

(4)a和p是M∞(A)中的兩個正元，其中p是一個投影，如果p?a，則存在M∞(A)中的元b使得p⊕b～a[12]。

定義1.1稱C*-代數(shù)A的Cuntz半群W(A)，具有投影的消去律，是指對于M∞(A)+中任意的正元a、b，任意的投影p，由a⊕p?b⊕p可以得到a?b[10]。

定義1.2稱C*-代數(shù)A的Cuntz半群W(A)具有弱消去律，是指對于M∞(A)+中的任意正元a、b、c和某個ε>0，由a⊕c?b⊕(c-ε)+，可以得到a?b[10]。

設(shè)Ω是一類C*-代數(shù)，則由Ω中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)類記為TAΩ。

定義1.3一個有單位元單的C*-代數(shù)A屬于TAΩ，是指對于任意的ε>0，任意的有限子集F?A，任意的a≥0，存在一個投影p∈A和A的C*-子代數(shù)B滿足1B=p和B∈Ω，使得

(1)對于任意的x∈F，||xp-px||<ε。

(2)對于任意的x∈F，pxp∈εB。

(3)[1-p]≤[a][3，5]。

定理1.2如果Ω類對于張量上一個矩陣代數(shù)封閉，且對于有單位元的可傳C*-子代數(shù)也是封閉的，則由Ω中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)類TAΩ，對于張量上一個矩陣代數(shù)封閉，且對于有單位元的可傳C*-子代數(shù)也是封閉的[3，5]。

下面的定理顯然，略去證明。

定理1.3C*-代數(shù)Cuntz半群的投影消去律和弱消去律可以遺傳到張量上一個矩陣代數(shù)和有單位元的可傳的C*-子代數(shù)中。

定義1.4A是一個無限維的可分的有單位元單的C*-代數(shù)，設(shè)α:G→Aut(A)是一個有限群G作用在C*-代數(shù)A上。稱α具有跡Rokhlin性質(zhì)，是指對于任意的有限子集F?A和任意的ε>0，任意的非零正元b∈A和任意的g∈G，存在相互垂直的投影eg∈A滿足

(1)對于任意的g,h∈G，||αg(eh)-egh||<ε。

(2)對于任意的d∈F，g∈G，||egd-deg||<ε。

(3)記e=∑g∈Geg，則投影1-e?b。

(4)||ebe||≥||b||-ε[13]。

2 主要結(jié)果

定理2.1設(shè)Ω是一類穩(wěn)定有限有單位元C*-代數(shù)，如果對于任意的B∈Ω，且B的Cuntz半群W(B)具有投影的消去律，則對于任意有單位元單C*-代數(shù)A∈TAΩ，A的Cuntz半群W(A)具有投影的消去律。

證明:設(shè)a和b是正元，p是投影，都在M∞(A)+中，滿足a⊕p?b⊕p，只要證明對于任意的ε>0，(a-3ε)+?b即可。

由定理1.1知，存在v∈A和δ′>0，滿足

v(diag((p-δ′)+b))v*=p+a

對于F={a,b,p,d,d*}，任意的δ>0，由于A∈TAΩ，存在A的C*-子代數(shù)B和非零投影q∈A，滿足B∈Ω和1B=q，使得

(1)對于任意的x∈F，||xq-qx||<δ。

(2)對于任意的x∈F，qxq∈δB。

由此可知，存在正元a′,b′,d′,d′*∈B，投影p′∈B，正元a″,b″,d″,d″*∈(1-q)A(1-q)和投影p″∈(1-q)A(1-q)，使得||a-a′-a″||<2δ，||b-b′-b″||<2δ，||a′+p′+a″+p″-(d″+d′)(b′+p′+b″+p″)(d′*+d″*)||<4δ。

因此可得到

||a′+p′-d′(b′+p′)d′*||<4δ

||a″+p″-d″(b″+p″)d″*||<4δ

由定理1.1得

(a′+p′-4δ)+?b′+p′

(a″+p″-4δ)+?b″+p″

因為a′,p′,b′,(a′-4δ)+∈B，并且B∈Ω，所以(a′-4δ)+?b′。

③[1-q-r]≤[(a′-4δ)+]。

由①和②可知，存在正元a?,b?,e?∈D，投影p?∈D，正元a″″,b″″,e″″∈(1-q-r)A(1-q-r)和投影p″″∈(1-q-r)A(1-q-r)，使得

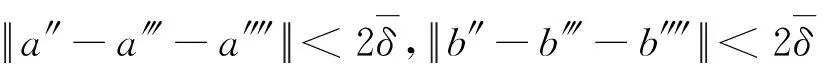
因此

從而有

(a-3ε)+?(a′-ε)++(a″-ε)+?

[p″″]+[c]+(a?-ε/3)++(a″″-ε/3)+?

[p″″]+[c]+b?+(a″″-ε/3)+?

因為ε>0是任意的，所以a?b。

定理2.2設(shè)Ω是一類有單位元的C*-代數(shù)，Ω對于有單位元可傳C*-子代數(shù)和張量上一個矩陣代數(shù)是封閉的。A∈TAΩ是一個無限維的單的有單位元的C*-代數(shù)，設(shè)α:G→Aut(A)是有限群G作用在一個C*-代數(shù)A上，并且作用具有跡Rokhlin性質(zhì)，則交叉積代數(shù)C*(G,A,α)在TAΩ中[14]。

推論2.1設(shè)A是一個穩(wěn)定有限無限維有單位元單的C*-代數(shù)，A的Cuntz半群W(A)具有投影的消去律。設(shè)α:G→Aut(A)是有限群G作用在C*-代數(shù)A上，并且作用具有跡Rokhlin性質(zhì)，則交叉積C*-代數(shù)C*(G,A,α)的Cuntz半群也具有投影的消去律。

定理2.3設(shè)Ω是穩(wěn)定有限有單位元的C*-代數(shù)類，并且對于任意的B∈Ω，B的Cuntz半群W(B)具有弱消去律，則對于任意有單位元單C*-代數(shù)A∈TAΩ，A的Cuntz半群W(A)也具有弱消去律。

證明：設(shè)a、b、c是M∞(A)+中的正元，滿足a⊕c?b⊕(c-δ)+，其中δ>0，則對于任意的ε>0，只要證明(a-3ε)+?b即可。

由定理1.2和定理1.3，不失一般性，假設(shè)a、b、c都在A中，并且ac=bc=0。不妨假設(shè)c是一個純正元，否則cCuntz等價于一個投影，由定理2.1和對于任意的δ>0，(p-δ)+=p，可以得到結(jié)論。

由于c是一個純正元，由定理1.1，存在正元g∈A，對于任意的δ″>0，使得

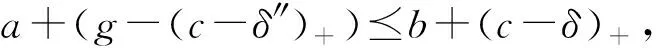
由定理1.1，存在v∈A和δ′>0，使得

由定理1.1，存在一個壓縮元d∈A，使得

對于F={a,b,c,g,d,d*}，任意的η>0，由于A∈TAΩ，存在A的C*-子代數(shù)B和非零的投影q∈A，滿足B∈Ω和1B=q，使得

(1)對于任意的x∈F，||xq-qx||<η。

(2)對于任意的x∈F，qxq∈ηB。

由此可知，存在正元a′,b′,g′,c′,d′,d′*∈B，正元a″,b″,c″,g″,d″,d″*∈(1-q)A(1-q)，使得

||a-a′-a″||<2η

||b-b′-b″||<2η

(c″-δ)+(d′*+d″*)||<6η

因此可以得到

d′(b′+(c′-δ)+)d′*||<6η

d″(b″+(c″-δ)+)d″*||<6η

由定理1.1知

a′+(g′-δ′-2δ″-6η)++c′?b′+(c′-δ)+

由于a′,c′,b′∈B，并且B∈Ω，可以得到a′+(g′-2δ′-δ″-6η)+?b′。

同樣的道理，存在e″∈(1-q)A(1-q)和δ?>0，使得

a″+g″+(c″-2δ′-δ″-2δ?-6η)+=

e″(b″+(c″-δ)+)e″*

③[1-q-r]≤[(g′-2δ′-δ″-6η)+]。

由此可知，存在正元a?,c?,b?∈D和正元a″″,c″″,b″″∈(1-q-r)A(1-q-r)，使得

取δ′,δ″,δ?,η，使得

||a?+g?+(c?-2δ′-δ″-2δ?-6η)++a″″+g″″+

(c″″-2δ′-δ″-2δ?-6η)+-(e?+e″″)(b?+

b″″+(c?-δ)++(c″″-δ)+)(e?+e″″)||<6δ

最后得到

||a?+g?+(c?-2δ′-δ″-2δ?-6η)+-

||a″″+g″″+(c″″-2δ′-δ″-2δ?-6η)+-

由定理1.1知

b?+(c?-δ)+

b″″+(c″″-δ)+)

(a-3ε)+?(a′-ε)++(a″-ε)+?

(g′-2δ′-δ″-6η)++(a′-ε)++(a?-ε/3)+?

因為ε>0是任意的，所以可以得到a?b。

推論2.2設(shè)A是一個無限維有單位元單的C*-代數(shù)，A的Cuntz半群W(A)具有弱消去律。設(shè)α:G→Aut(A)是有限群G作用在C*-代數(shù)A上，且作用具有跡Rokhlin性質(zhì)，則交叉積C*-代數(shù)C*(G,A,α)的Cuntz半群具有弱消去律。

3 結(jié) 論

本文得到了如下的結(jié)論：(1)設(shè)Ω是一類Cuntz半群具有弱消去律的C*-代數(shù)。證明了Cuntz半群的弱消去律可以遺傳到由Ω中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)類TAΩ中。(2)設(shè)Ω是一類Cuntz半群具有投影消去律的C*-代數(shù)。證明了Cuntz半群的投影消去律可以遺傳到由Ω中的C*-代數(shù)跡逼近之后得到的C*-代數(shù)類TAΩ中。

作為上述結(jié)論的應(yīng)用得到了如下結(jié)果：(1)如果A是一個無限維有單位元單的Cuntz半群具有弱消去律性質(zhì)的C*-代數(shù)，且設(shè)α:G→Aut(A)是有限群G作用在C*-代數(shù)A上并且作用具有跡Rokhlin性質(zhì)，則交叉積C*-代數(shù)C*(G,A,α)的Cuntz半群具有弱消去律。(2)如果A是一個無限維有單位元單的Cuntz半群具有投影消去律的C*-代數(shù)，且設(shè)α:G→Aut(A)是有限群G作用在C*-代數(shù)A上并且作用具有跡Rokhlin性質(zhì)，則交叉積C*-代數(shù)C*(G,A,α)的Cuntz半群具有投影消去律。