鋼筋混凝土梁彎曲開裂后有效剛度計算

谷守經(jīng)，張志華

（天津市政工程設(shè)計研究總院有限公司，天津 300392）

鋼筋混凝土具有良好的材料整體性、耐火性、耐久性且施工簡便，所以許多橋梁都采用鋼筋混凝土結(jié)構(gòu)。橋梁在正常使用過程中所發(fā)生的損傷主要是由混凝土或鋼筋性能退化引起的，其中混凝土的開裂[1]是造成結(jié)構(gòu)損傷的主要原因，研究如何準(zhǔn)確評價混凝土結(jié)構(gòu)開裂后的使用性能[2]，具有重要意義。基于黏結(jié)滑移理論、無滑移理論、綜合理論和數(shù)理統(tǒng)計方法，國內(nèi)外學(xué)者對開裂混凝土結(jié)構(gòu)進行了大量的試驗研究及理論推導(dǎo)[3～6]，提出多種關(guān)于混凝土結(jié)構(gòu)荷載裂縫的計算公式[7～8]，在各自的研究范圍內(nèi)，理論值計算結(jié)果均與試驗值吻合較好，極大簡化了混凝土結(jié)構(gòu)荷載裂縫的計算方法[9～10]。但大部分研究的是平均剛度計算公式，不能準(zhǔn)確描述每個梁截面的剛度變化。本文針對鋼筋混凝土受彎開裂情況，基于基本假設(shè)，建立開裂截面平衡方程，求解截面有效慣性矩，提出精確計算開裂截面有效剛度的計算公式并將理論推導(dǎo)計算值與現(xiàn)行規(guī)范計算值進行對比，驗證所提出公式準(zhǔn)確性。

1 理論推導(dǎo)

1.1 基本假設(shè)

1.1.1 本構(gòu)關(guān)系

鋼筋應(yīng)力

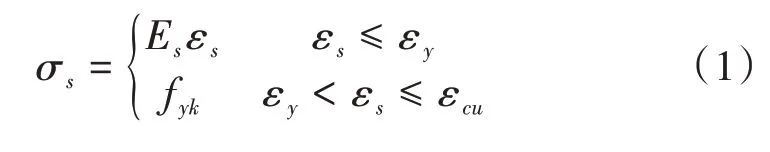
式中：fyk為屈服強度標(biāo)準(zhǔn)值；Es為鋼筋彈性模量；εs為鋼筋應(yīng)變；εy為鋼筋屈服應(yīng)變；εcu為鋼筋極限拉應(yīng)變。

在混凝土梁截面開裂后，考慮受拉區(qū)混凝土的作用，混凝土單軸受拉/受壓應(yīng)力-應(yīng)變關(guān)系采用我國混凝土結(jié)構(gòu)設(shè)計規(guī)范[11]推薦本構(gòu)曲線。見圖1。

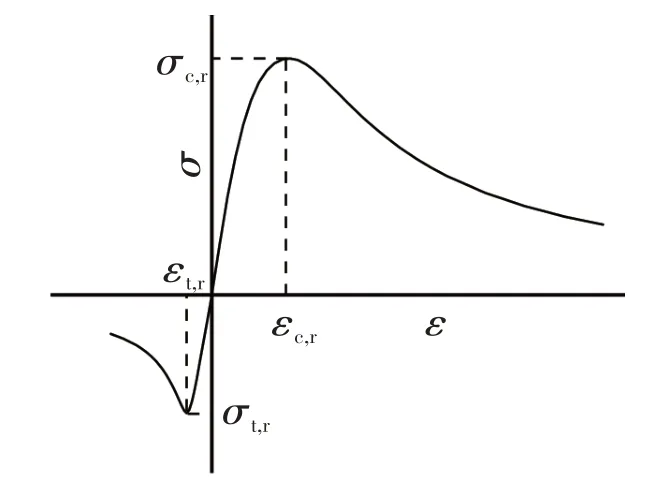
圖1 混凝土單軸受拉/受壓時應(yīng)力-應(yīng)變關(guān)系

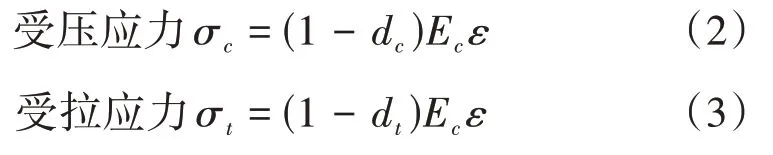
式中：dc為混凝土單軸受壓損傷演化參數(shù)；dt為混凝土單軸受拉損傷演化參數(shù)；ε為混凝土應(yīng)變；Ec為鋼筋彈性模量。

1.1.2 平截面假設(shè)

梁的正截面在受力發(fā)生彎曲變形后，仍保持平截面，平行于梁中和軸的各縱向纖維應(yīng)變與其到中和軸的距離成正比，鋼筋與其同一水平線的混凝土應(yīng)變相等。

1.1.3 應(yīng)力狀態(tài)

鋼筋和混凝土受壓區(qū)應(yīng)力均未達到應(yīng)力曲線峰值，受拉區(qū)邊緣混凝土已達到峰值拉應(yīng)變。

1.2 建立計算方程

當(dāng)荷載達到開裂彎矩以后，截面受壓區(qū)合力

式中：xc為受壓區(qū)高度；b為矩形截面寬度。受壓區(qū)合力至中性軸的距離

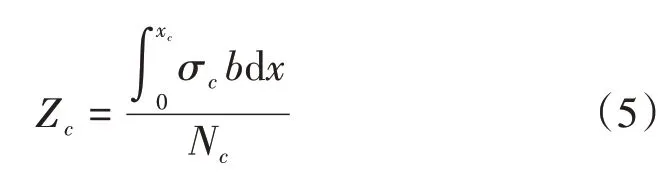
梁截面受拉區(qū)合力

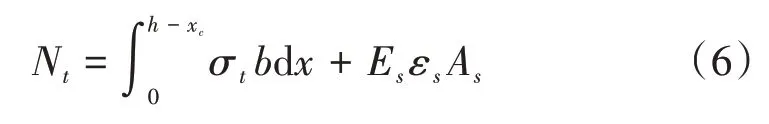
式中：h為矩形截面高度；As為受拉區(qū)配筋面積。

梁截面受拉區(qū)合力至中性軸的距離

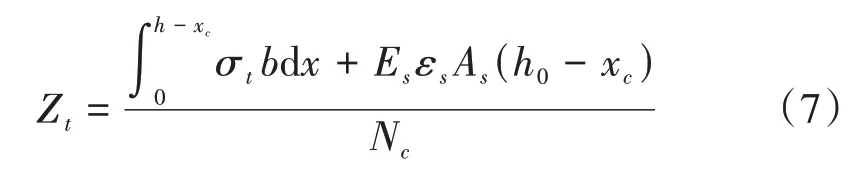
式中：h0為矩形截面有效高度。

建立平衡方程

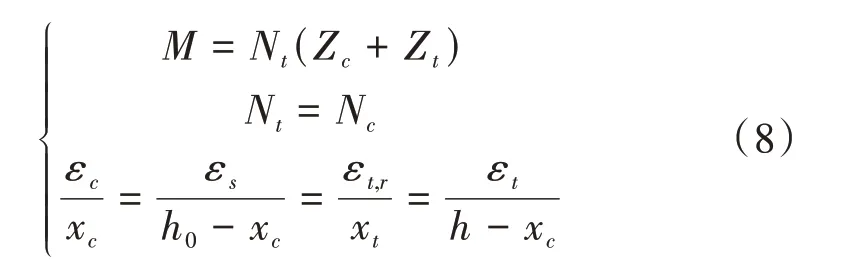
式中：M為截面所受彎矩；?c為受壓區(qū)混凝土邊緣壓應(yīng)變；xt為受拉區(qū)混凝土屈服應(yīng)變位置至中性軸的距離；?tr為混凝土屈服拉應(yīng)變；?t為受拉區(qū)混凝土邊緣拉應(yīng)變。

根據(jù)式（8），計算63種不同配筋率、混凝土強度、高寬比的鋼筋混凝土梁正截面M/Mcr-Ie/I0；Mcr為截面開裂彎矩；Ie為開裂截面有效抗彎慣性矩；I0為未開裂截面抗彎有效慣性矩。見表1和圖2-圖4。

圖2 C30混凝土開裂后截面M/Mcr-Ie/I0計算曲線

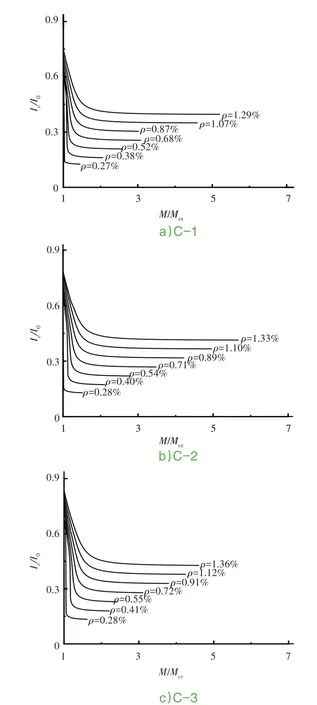
圖4 C50混凝土開裂后截面M/Mcr-Ie/I0計算曲線

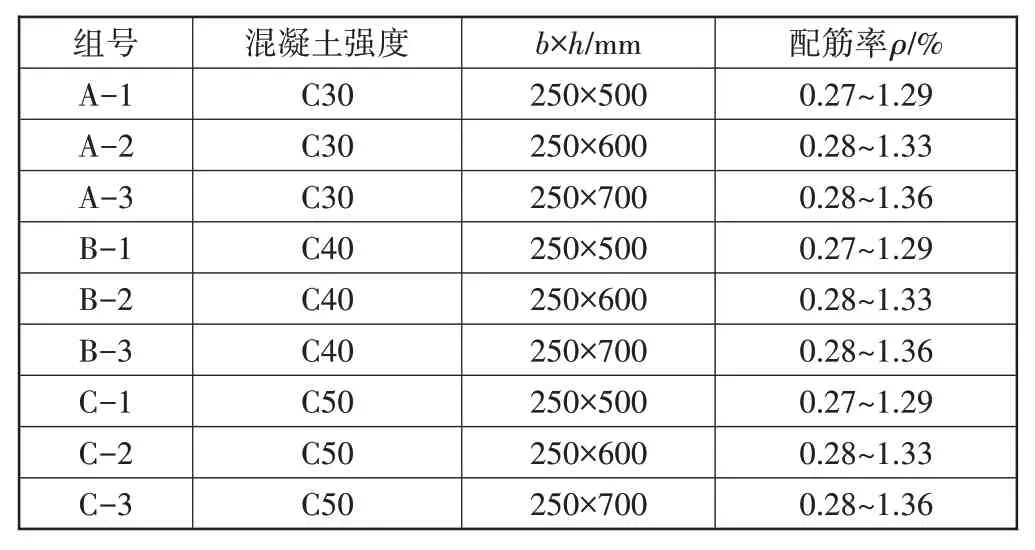
表1 截面計算數(shù)據(jù)

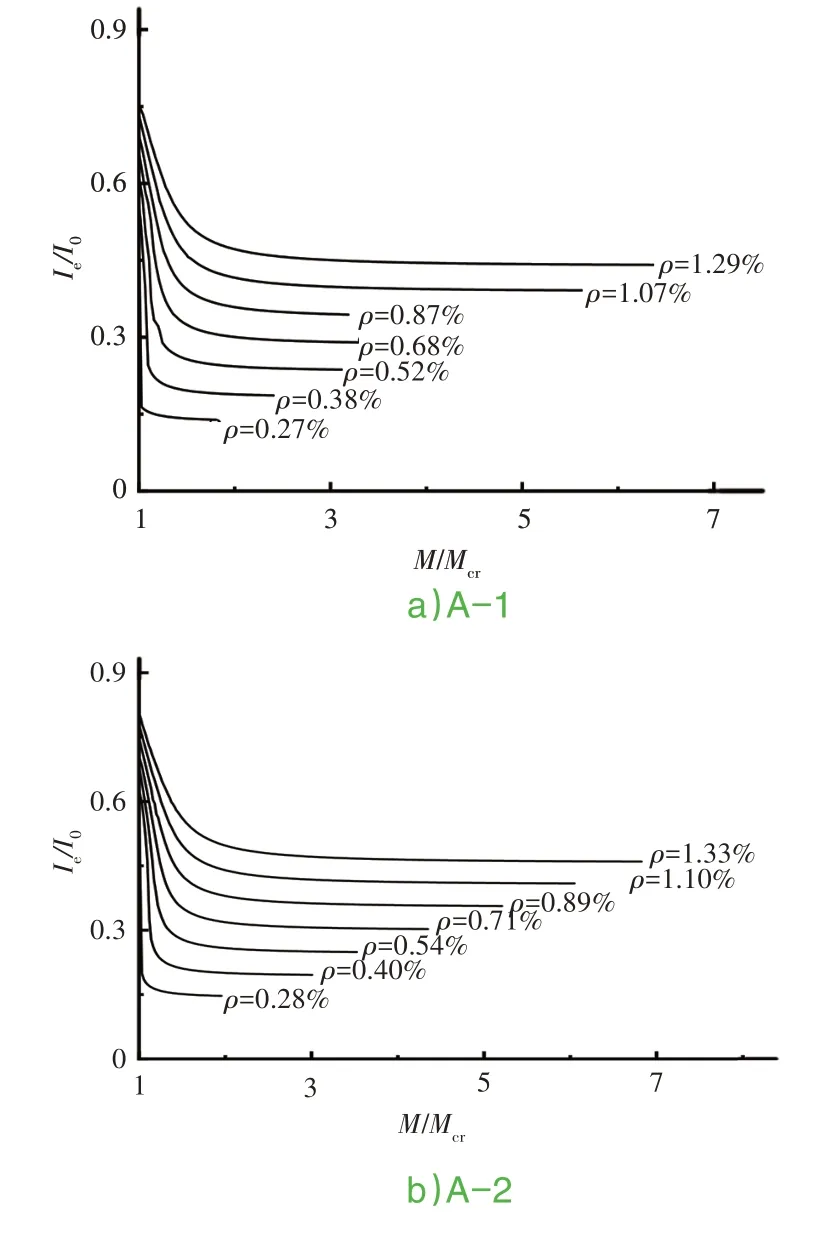
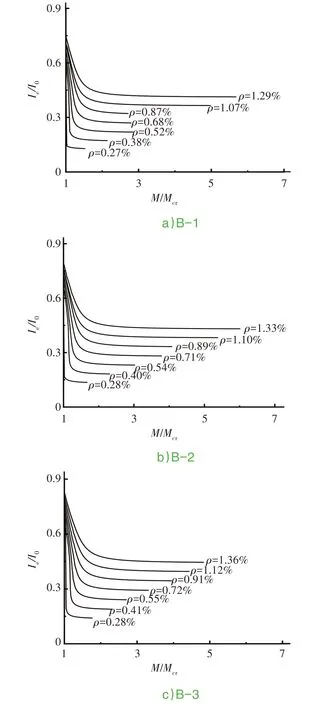
圖3 C40混凝土開裂后截面M/Mcr-Ie/I0計算曲線

1.3 限值計算

由以上計算結(jié)果可知，混凝土梁在達到開裂彎矩時，截面慣性矩已經(jīng)發(fā)生衰減[12]，在受拉鋼筋屈服之后，截面有效慣性矩逐漸趨于穩(wěn)定，故本文規(guī)定當(dāng)M=Mcr時，截面剛度為開裂后有效慣性矩上限值Imax；當(dāng)受拉區(qū)鋼筋屈服時，截面剛度為開裂后有效慣性矩下限值Imin。上限值與混凝土截面高寬比及配筋率有關(guān)，與混凝土強度無關(guān)；下限值與混凝土強度及配筋率有關(guān)，與截面高寬比無關(guān)。根據(jù)計算結(jié)果，建立限值計算基本公式，式中計算參數(shù)由擬合確定。

上限值截面有效慣性矩，當(dāng)M=Mcr時，截面有效慣性矩

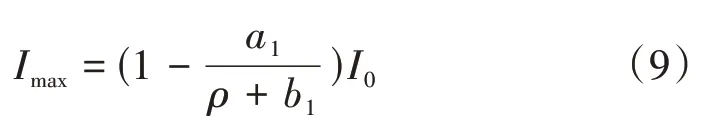
式中：a1與截面高寬比有關(guān),a1=0.56(b/h-0.5)+0.12；b1為計算常數(shù)，取b1=0.77。

當(dāng)Imax/I0＞0.85時，取Imax=0.85。

根據(jù)式（9）計算不同截面開裂后的有效慣性矩上限值Imax，見圖5。

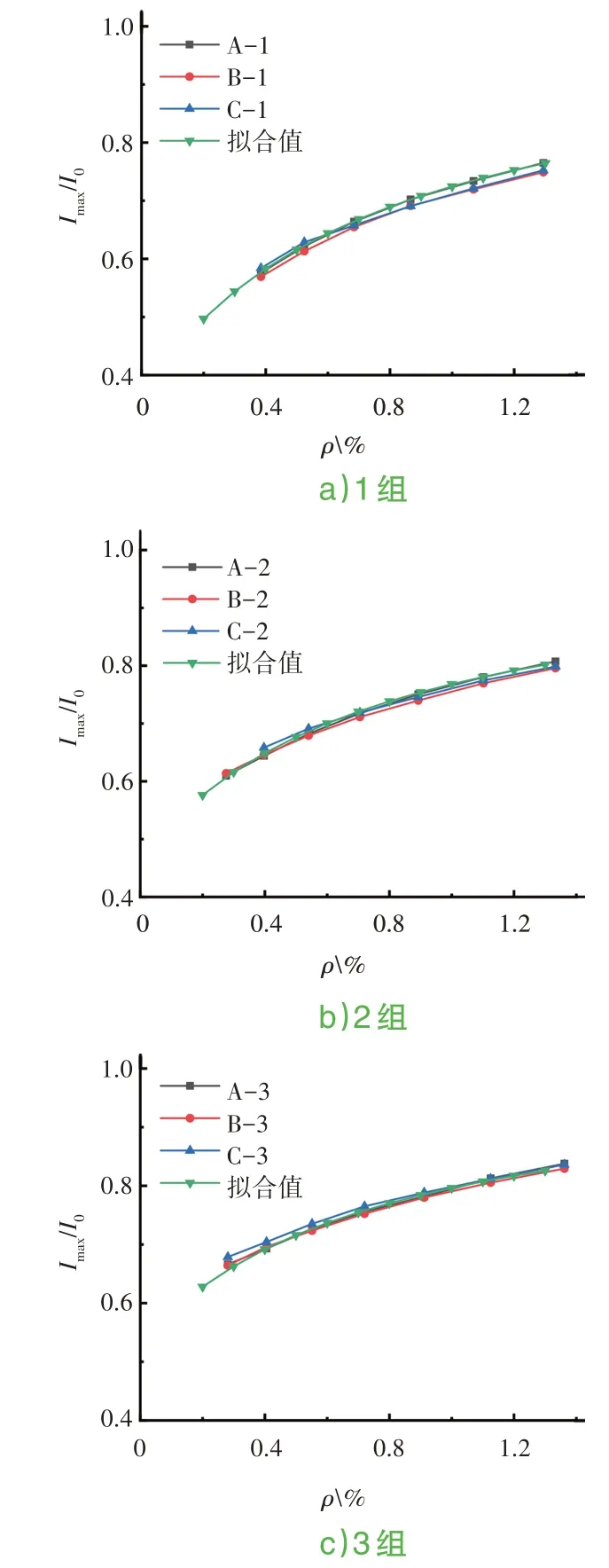
圖5 M=Mcr時Imax/I0與配筋率計算關(guān)系

下限值截面有效慣性矩

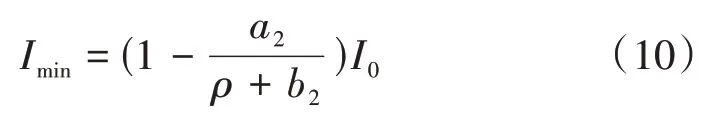
式中：計算參數(shù)a2和b2與混凝土強度有關(guān)，見表2。

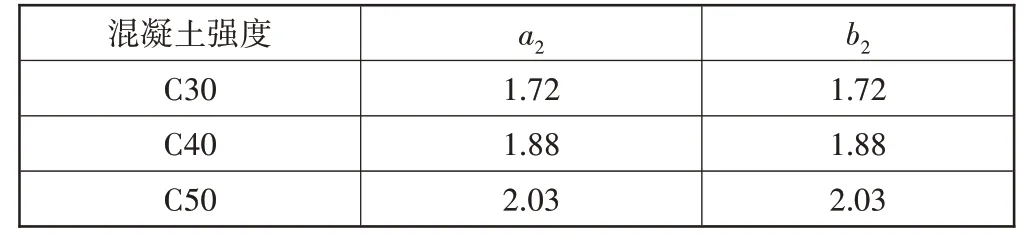
表2 Imax計算參數(shù)取值

根據(jù)式（10）計算不同截面開裂后的Imin，見圖6。

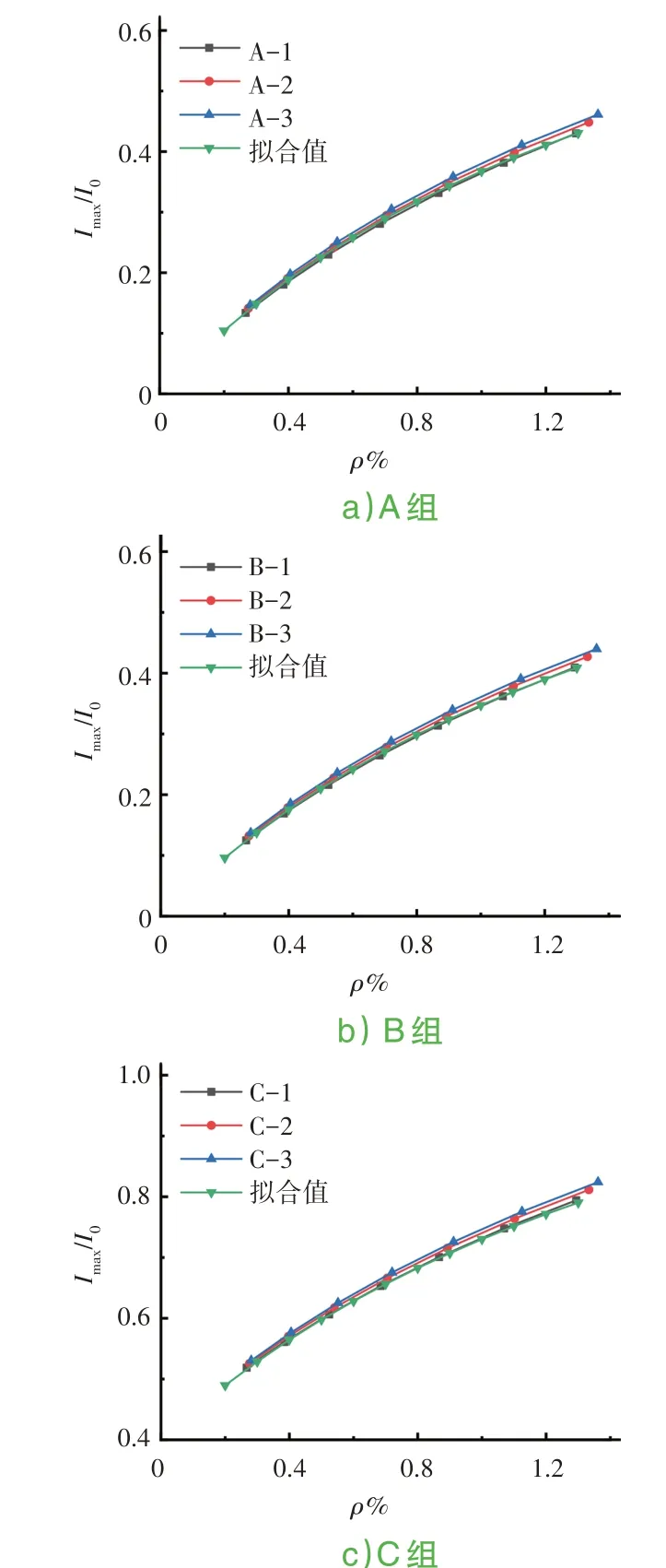
圖6 鋼筋屈曲時Imin/I0與配筋率計算關(guān)系

1.4 混凝土開裂后M/Mcr-Ie/I0關(guān)系計算

鋼筋混凝土梁開裂后，截面有效慣性矩在Imax和Imin之間變化，截面有效慣性矩衰減速率與截面配筋率有關(guān)，對圖2-圖4的計算結(jié)果進行擬合，建立梁截面M-Ie的曲線公式。

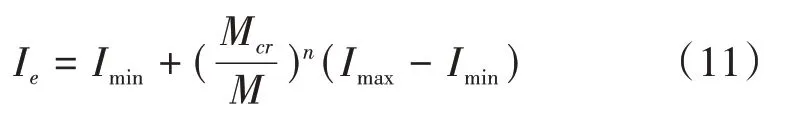
式中：n與截面配筋率有關(guān)；Ie為截面有效抗彎慣性矩。

根據(jù)式（11）計算面開裂后的M/Mcr-Ie/I0，見圖7。

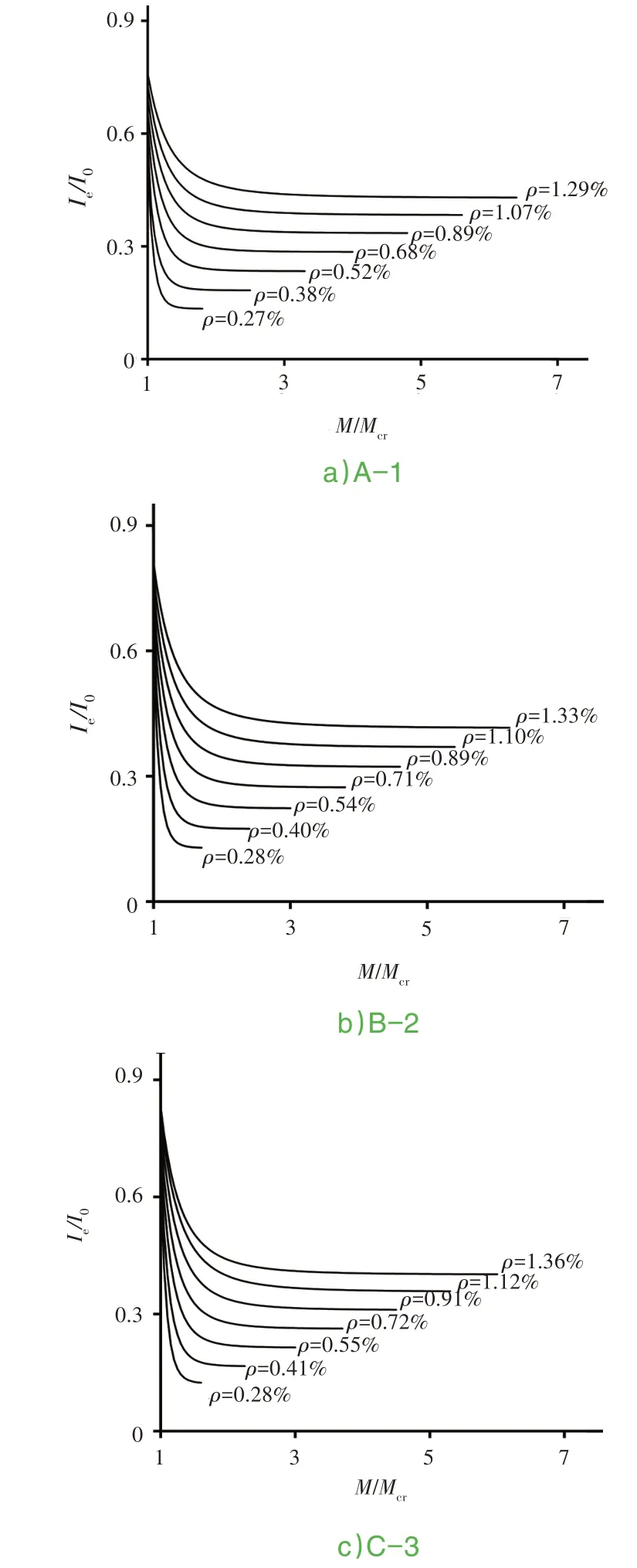
圖7 混凝土開裂后截面M/Mcr-Ie/I0計算曲線

2 算例

進行撓度計算時，鋼筋混凝土簡支梁長L取6 m，進行四點彎曲加載，梁截面取不同高寬比、配筋率、混凝土強度的參數(shù)。見圖8和表3。

圖8 四點彎矩加載計算

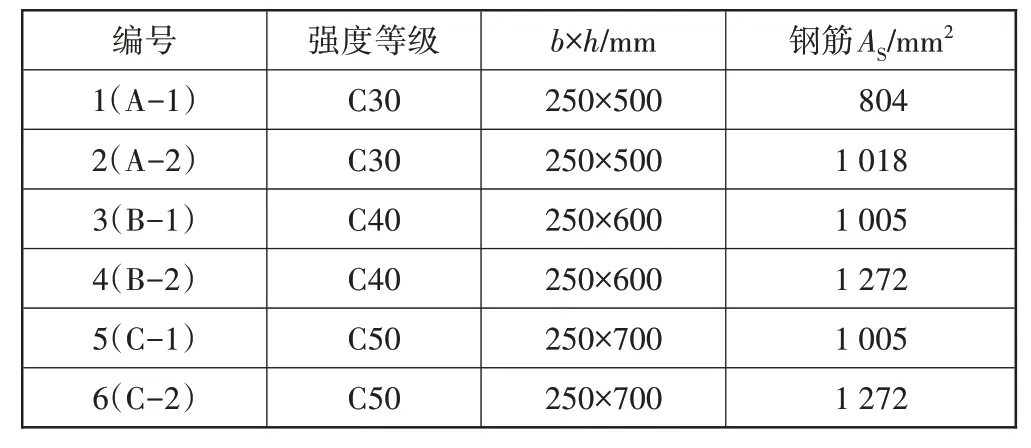
表3 截面計算參數(shù)

計算時,未達到開裂彎矩的梁截面有效剛度B0取0.85EcI0。

采用本文提出的公式與4種規(guī)范[12～15]計算公式及有限元模擬值進行對比，由計算結(jié)果可知，在鋼筋混凝土梁荷載達到開裂彎矩以后，推導(dǎo)計算撓度值與規(guī)范計算撓度值極為接近，說明本文推導(dǎo)公式計算結(jié)果與實際相符，可應(yīng)用到實際工程中。見圖9。

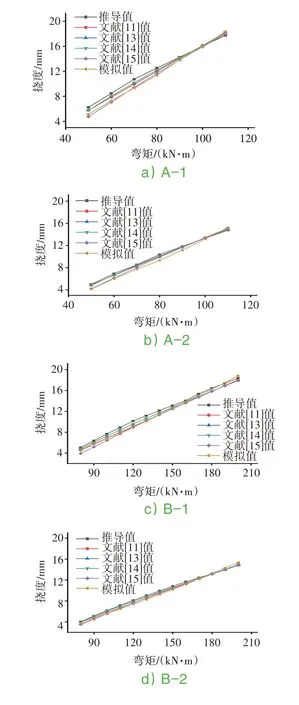
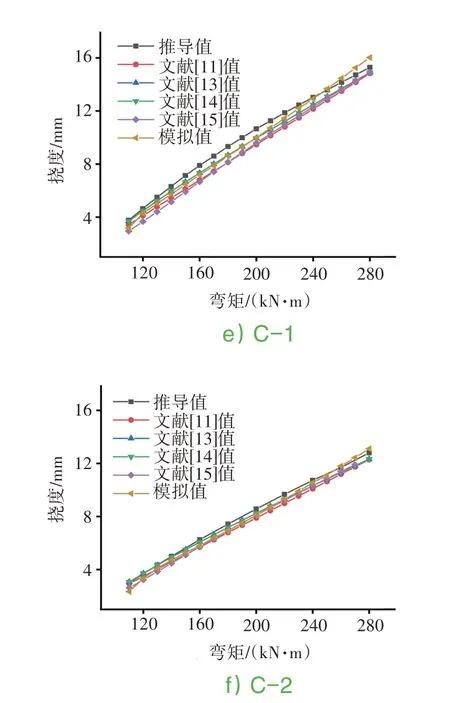
圖9 彎矩-撓度

3 結(jié)論

1）鋼筋混凝土梁所受荷載在達到開裂荷載以前，截面抗彎剛度已經(jīng)發(fā)生了退化。荷載達到開裂荷載時，受拉區(qū)縱向鋼筋配筋率相同時，其有效抗彎剛度剛度上限值（M=Mcr）與截面高寬比有關(guān)，截面b/h越大，其剛度比值Imax/I0越大；剛度下限值（受拉區(qū)鋼筋屈服時）與混凝土強度有關(guān)，混凝土強度越高，其剛度比值Imin/I0越小。

2）鋼筋混凝土梁在達到開裂荷載以后，其有效抗彎剛度值與配筋率有關(guān)，相同截面尺寸條件下，受拉區(qū)縱向鋼筋配筋率越大，其有效抗彎剛度值越大。

3）鋼筋混凝土梁開裂后，隨荷載的進一步增大，抗彎剛度在前期下降迅速，而后期下降逐漸平緩直至趨于穩(wěn)定；截面有效剛度下降速率與受拉區(qū)縱向鋼筋配筋率有關(guān)，配筋率越高，剛度下降速率越慢。

4）利用本文提出鋼筋混凝土梁開裂后有效剛度計算公式進行四點彎曲算例分析，結(jié)果證明了本文提出計算方法的準(zhǔn)確性，所以采用本文計算方法所得數(shù)據(jù)可作為實際工程計算的參考。