Accurate theoretical evaluation of strain energy of all-carboatomic ring(cyclo[2n]carbon),boron nitride ring,and cyclic polyacetylene

Tian Lu(盧天) Zeyu Liu(劉澤玉) and Qinxue Chen(陳沁雪)

1Beijing Kein Research Center for Natural Sciences,Beijing 100024,China

2School of Environmental and Chemical Engineering,Jiangsu University of Science and Technology,Zhenjiang 212100,China

Keywords: strain energy, ring strain, cyclo[18]carbon, boron nitride ring, cyclic polyacetylene, quantum chemistry

1. Introductio n

Strain energy (SE) is a critical property of cyclic molecules,which measures the potential energy released during the transformation of a molecule from its equilibrium cyclic structure to a hypothetical unstressed(strainless)structure. SE is closely related to stability,reactivity,and synthetic accessibility of molecules.[1]Compared to analogous systems,usually the higher the SE of a molecule, the lower its stability, the higher its reactivity, and the more difficult it is to be synthesized. Due to the importance of the concept of SE, it has been widely discussed in studies of cyclic molecules.[2–6]SE can not only be qualitatively anticipated based on molecular structure and common knowledge of chemical theory, but also be quantitatively estimated by various methods based on experimental thermodynamic data or theoretical calculation results.[1,7–10]

Cyclo[18]carbon is a ring molecule consisting of 18 carbon atoms. Its existence was predicted theoretically as early as 1966 by Hoffmann,[11]but it was not observed in the condensed phase until 2019.[12,13]Since cyclo[18]carbon has very different electronic structure and geometric character from common chemical systems, theoretical chemists have extensively investigated its properties by quantum chemical methods, see Refs. [14–23] for examples. We have also conducted comprehensive research on cyclo[18]carbon as well as its derivatives in recent years, including bonding,[24,25]aromaticity,[24,25]electronic excitation,[26,27]nonlinear optical properties,[26–28]vibrational characteristics,[29]intermolecular interactions,[30,31]and so on.[32–35]As far as we know,cyclocarbon molecules larger than cyclo[18]carbon have not been experimentally observed yet;despite this,they are expected to be stably existent at least in vacuum. In Fig.S1 of our recent work,[28]we have showed that average atomization energy of cyclo[2n]carbon systems increases withn. In this regards,cyclocarbons larger than cyclo[18]carbon may be even more stable.

The atoms in all-carboatomic ring systems, namely the cyclocarbons, are in sp-hybrided state. It is evident that the ideal angle consisting of this type of carbon is 180?,so the cyclocarbon systems must show a ring strain effect. An accurate study of SE of the cyclocarbon of different sizes is of great importance for the in-depth understanding of their intrinsic characteristics and the synthesis of their derivatives in the future.However, so far as we know, no systematical study of the SE of the cyclocarbon has been reported. In this work, we will carefully investigate the relationship between SE and ring size based on highly accurate quantum chemistry calculations and reliable estimation model to fill this important gap.In addition,we will also compare the ring strain of cyclocarbon with that of two kinds of interesting systems very closely related to it,namely boron nitride ring(BN ring)and cyclic polyacetylene(c-PA),see Fig.1(a)for their schematics and Fig.1(b)for optimized three-dimensional structures of representative systems.The BN ring containing alternating boron and nitrogen atoms can be regarded as an isoelectronic analogue of cyclocarbon,in particular,B9N9has already received special attentions and has been theoretically studied recently.[36,37]Since electronic structure of BN ring is notably different from that of cyclocarbon, it is expected that their ring strain characteristics should exhibit great difference. c-PA is a novel polymer synthesized in 2021,[38]unlike the widely studied annulene systems,[5,39]which contain bothcisandtransdouble bonds,it was experimentally proven that c-PA shows all-transconfiguration. This structure characteristic implies that c-PA should form a global in-planeπconjugation like the cyclocarbon,while the out-ofplaneπconjugation of cyclocarbon is lacking in c-PA.The difference of ring strain between c-PA and cyclocarbon is an interesting question,we will reveal the answer by studying their SEs in this paper.

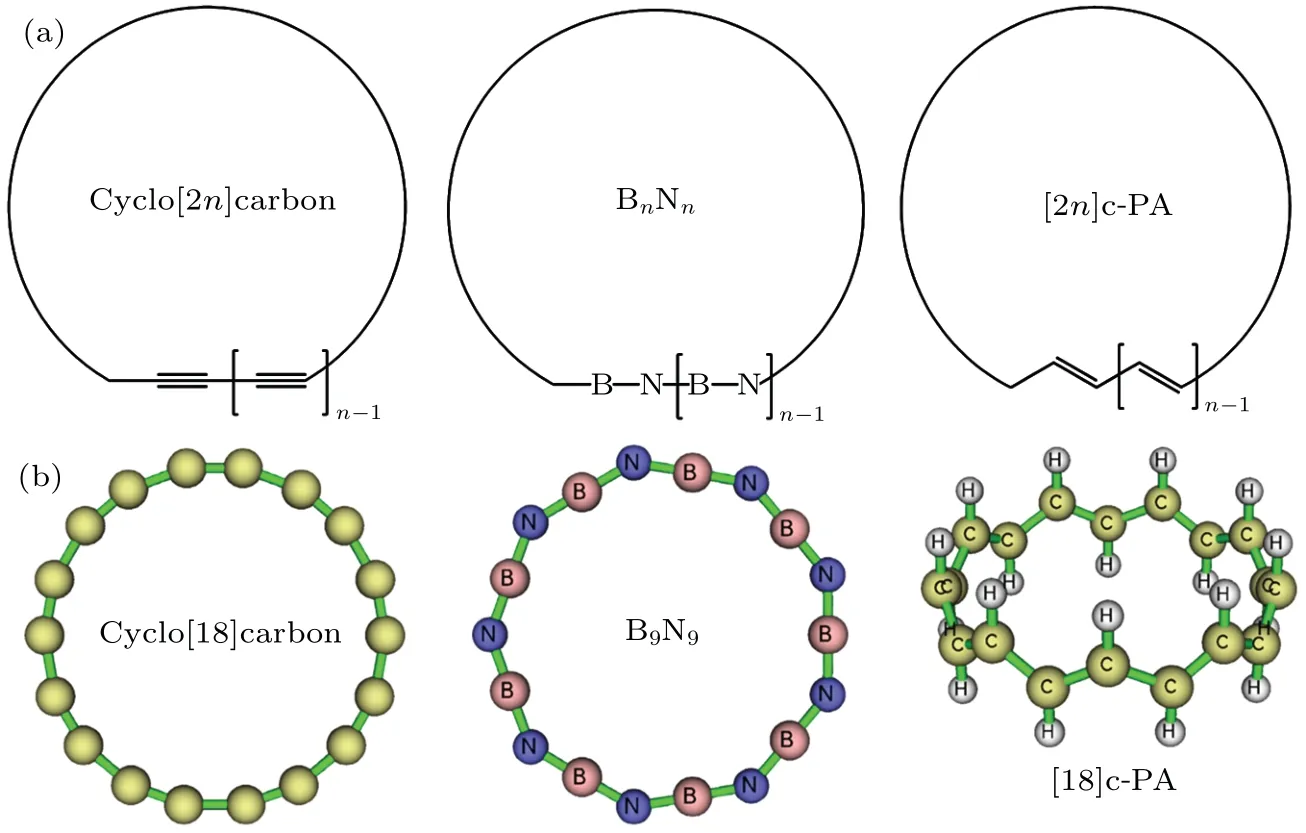
Fig. 1. (a) Scheme of cyclocarbon, BN ring, and c-PA. (b) Geometry of cyclo[18]carbon, B9N9 ring, and [18]c-PA molecules optimized at ωB97XD/def2-TZVP level, all of them correspond to n=9. Note that the cyclocarbon systems do not actually consist of alternating single and triple C–C bonds as illustrated by the Lewis structure in the scheme,see Ref.[24]for detailed analysis of its bonding character. Also,[18]c-PA does not strictly consist of alternating single and double C–C bonds as indicated by the Lewis structure,see the main text for discussion.

In the rest of this article, Section 2 will describe computational details,Section 3 will explore relationship between SE and the number of repeat units for cyclocarbon systems.Sections 4 and 5 will examine SEs of BN ring and c-PA of different sizes, respectively, and meantime similarity and difference of ring strain between them and cyclocarbon will be discussed. In Section 6,we will summarize the whole article.

2. Computational details

All geometries involved in this study were optimized by density functional theory (DFT) method viaωB97XD exchange–correlation functional[40]in combination with the high quality def2-TZVP basis set.[41]We have demonstrated that this computational level is able to well reproduce experimental observation of geometry of cyclo[18]carbon,[24]and the same calculation strategy has been employed by us in investigation of much larger cyclocarbons.[28,29]In addition,ωB97XD was shown to be a good choice for representing wide variety of delocalized systems,[42,43]therefore it is expected to present satisfactory geometries for BN ring and c-PA. After geometry optimizations, frequency analyses were conducted for all systems to confirm that there is no imaginary frequency and thus the obtained geometries indeed correspond to minimum structures. Geometry optimizations and frequency analyses in this work were conducted by Gaussian 16 A.03 program.[44]As already mentioned in Ref.[28],when number of repeat unitsnis large enough(≥8),cyclo[2n]carbon showsDnhsymmetry. All BnNnand [2n]c-PA molecules optimized in this work showDnhandDnsymmetries,respectively.

Obtaining high precision electronic energies is a prerequisite for achieving a reasonable estimation of SE, and this is especially true for systems with unusual electron structure. Unless otherwise specified, all electronic energies involved in this work were calculated by DLPNO-CCSD(T)method with tightPNO setting[45]in combination with ccpVTZ basis set.[46]The DLPNO-CCSD(T) is a well-known low-order scaling variant of the very accurate but extremely expensive CCSD(T)method,it can be applied to significantly larger systems than CCSD(T)without notable sacrifice in accuracy.ORCA 5.0.3 program was used to realize the DLPNOCCSD(T)calculation.[47]

All electronic structure analyses and plots of threedimensional maps were realized by Multiwfn 3.8 program[48]based on wavefunctions and geometries produced atωB97XD/def2-TZVP level.

3. Results and discussion

3.1. Strain energy of cyclo[2n]carbon

First, it should be noted that there is no unique way to evaluate SE of a cyclic system. A popular way to derive SE is building a proper homodesmotic reaction,[1,8,9]so that its reaction energy fully reflects the energy difference between the current cyclic structure and the fictitious status in which geometry distortion caused by the cyclization is fully released.If this method is applied to cyclo[2n]carbon (C2n), then the reaction to be calculated should be

This reaction corresponds to transplanting each repeat unit(CC) of cyclocarbon into a carbyne of finite length saturated by hydrogens at the two ends. The finite carbyne is chosen as the reactant because the atoms in this system also show sp-hybridzation state like the cyclocarbon and meantime this system is free of strain. However, it was shown that the homodesmotic reaction method does not work well for highly conjugated cyclic system such as carbon nanobelt,[1]a main possible reason is the non-negligible difference of chemical environment that the repeat unit felt in the cyclic system and in the product. In addition,from Eq.(1)it is clear that the SE evaluated in the above way must be more or less dependent ofm,while the choice ofmis somewhat arbitrary,so the principle of the homodesmotic reaction method is not rigorous. To illustrate these points, we plotted the variation of SE of cyclo[18]carbon with respect tomas shown in Fig. 2(a), it can be seen that the SE is indeed affected by the choice ofmespecially whenmis small. Moreover, as illustrated by Fig.2(b),irrespective of the choice ofm, the lengths of the short and long C–C bonds in the product molecule HC2m(CC)C2mH always differ from those in cyclo[18]carbon with a nonnegligible extent,implying that the SE evaluated via Eq.(1)must be unexpectedly polluted by additional energy variation caused by change of bonding status. So, equation (1) is far from an ideal way of estimating SE of cyclocarbon.

The regression analysis method extensively employed by Segawa and coworkers in studying SE of conjugated carbon nanobelt[1]is a physically sound way of evaluating SE of cyclocarbons. In common cases, to use this method to obtain SE, one should calculate energy per repeat unit (E·n?1) for a series of cyclic systems of different sizes, and then obtainE·n?1of infinite large ring(strainless ring)by extrapolation,which will be referred to asEinf·n?1later. After that,SE per repeat unit (SE·n?1) for a cyclic system with a specific size can be evaluated by taking difference between itsE·n?1andEinf·n?1, and finally, SE of the system can be calculated by multiplying the SE·n?1by actual number of repeat units in the ring.

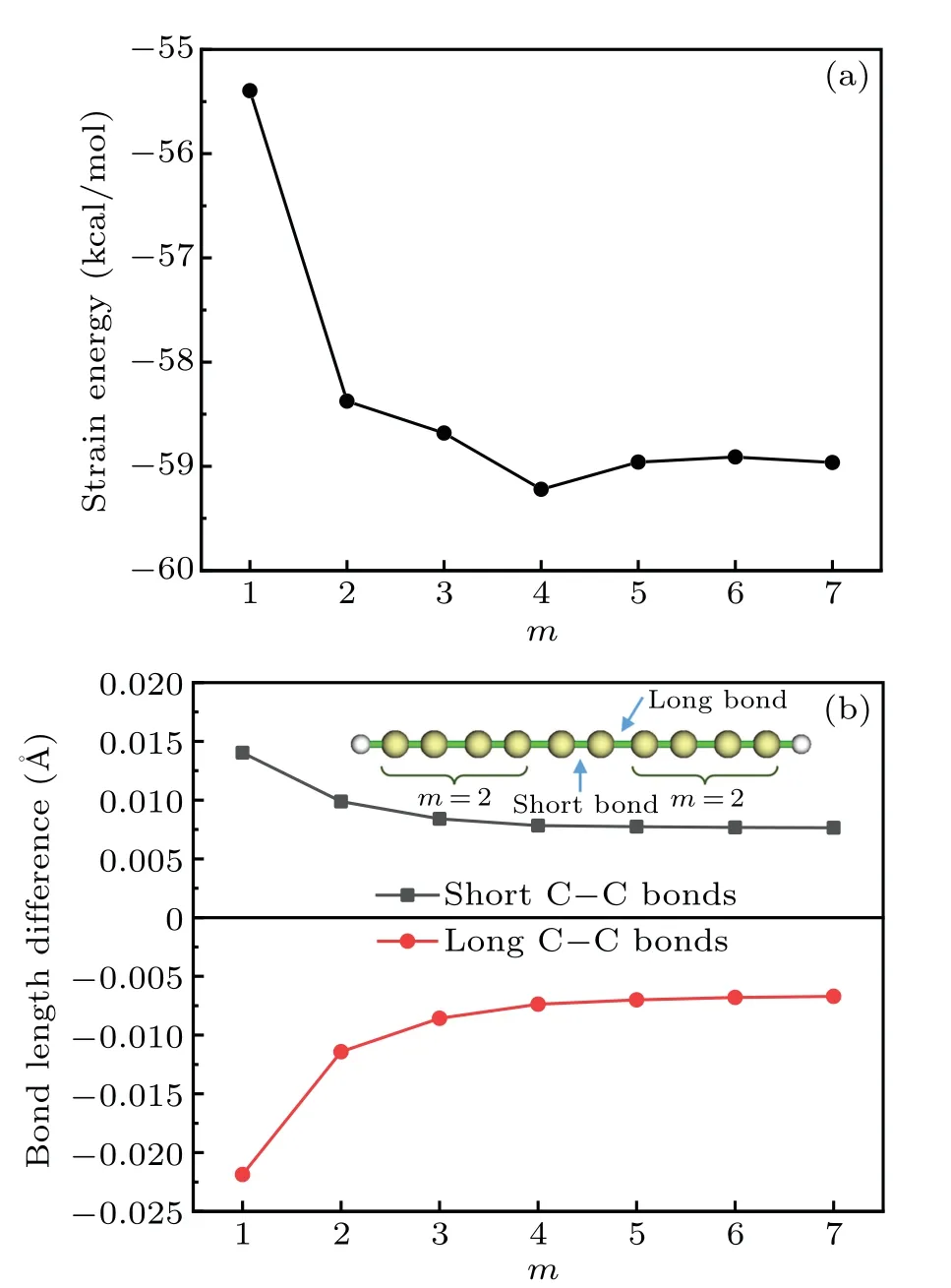
Fig. 2. (a) Strain energy of cyclo[18]carbon evaluated using Eq. (1)with different m. (b) Difference of C–C bond lengths between C18 and HC2m(CC)C2mH with different m. The short and long bonds in the HC2m(CC)C2mH used in calculating bond length differences are indicated in the inset with m=2 as example.

Special attention should be paid when employing the regression analysis to derive SE of cyclocarbons due to their unusual electronic structure. In our viewpoint, there are three factors simultaneously influencingE·n?1: (i) Intramolecular interactions, including steric, dispersion, and electrostatic effects. (ii) Status of electronic structure or bonding character.(iii) Strain effect. In order to strictly derive SE based on regression analysis, only the factor (iii) should play the dominant role for the considered systems. Although the factor (i)can be safely ignored as long as the ring is not very small, a careful examination of factor(ii)should not be overlooked,especially for the systems with globally delocalizedπelectrons like the cyclocarbon.[24]We plotted variation of bond length of cyclo[2n]carbon with respect to the number of repeat unitsnas shown in Fig.3. It can be seen that the bond length fluctuates sharply asnincreases whennis not large, indicating that bonding character is heavily affected bynin this situation. The bond length is basically converged whennis equal to or larger than 13, reflecting essentially identical electronic structure among sufficiently large cyclocarbons. Therefore,in order to exclude the effect of factor(ii)and represent only the factor(iii)in the regression analysis,only cyclo[26]carbon and larger ones should be taken into account.

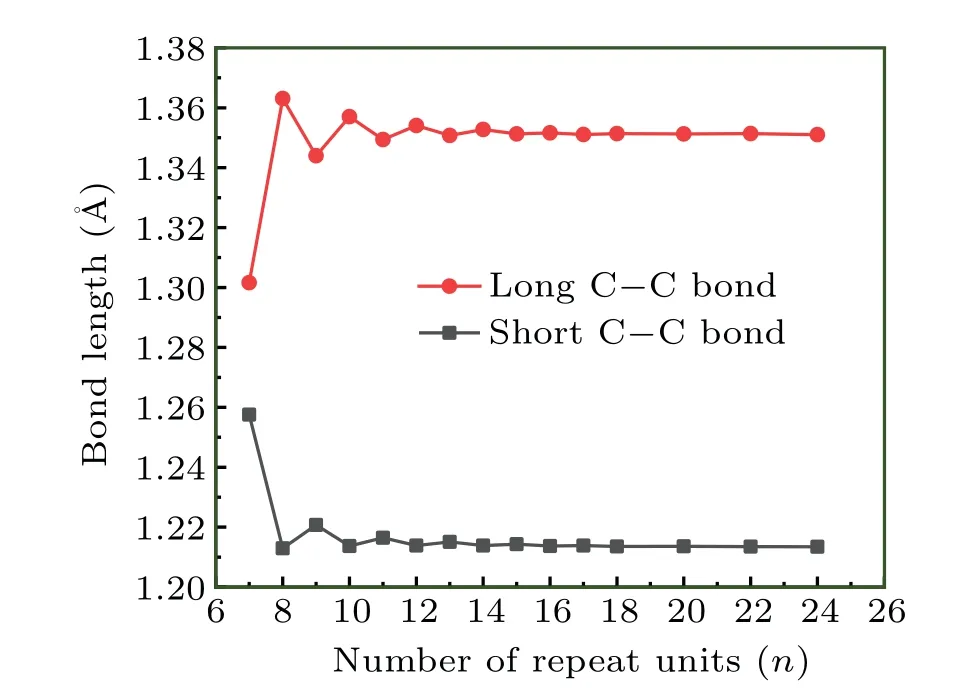
Fig.3. Bond length of cyclo[2n]carbon with different n.

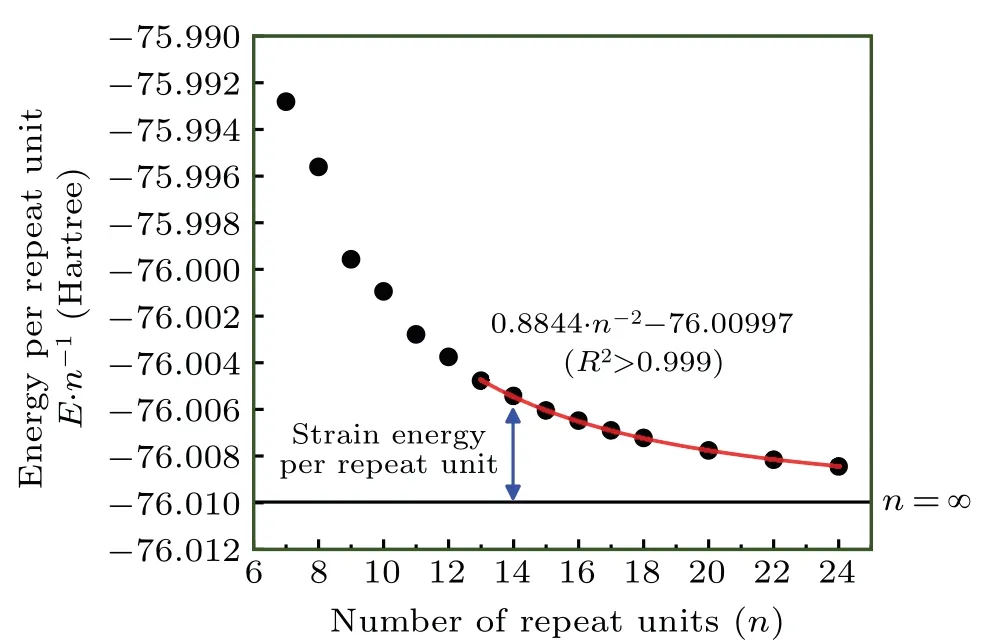
Fig.4. Energy per repeat unit of cyclo[2n]carbon with different n. The red curve portrays the relationship fitted for points of n ≥13.

We calculatedE·n?1for a series of cyclo[2n]carbon systems ranging from a small ring (n=7) to a fairly large ring(n=24), see Fig.4. Due to the aforementioned reason, only the systems withn ≥13 are included in the regression analysis,and regression equationEfit·n?1=A·n?2+Bis adopted.[1]The red curve in Fig. 4 portrayed the fitted relationship, one can see that the fitting quality is perfect, withR2even larger than 0.999. It is evident that the parameterBcan be directly viewed as theEinf·n?1mentioned earlier, while theA·n?2term corresponds to the SE·n?1because of the relation SE·n?1=Efit·n?1?Einf·n?1. It is also obvious that SE of a ring containingnrepeat units is simply equal toA·n1,because SE corresponds to product of SE·n?1andn. From the fitted equation given in Fig.4,we know cyclo[2n]carbon system has SE of 0.8844·n?1Hartree or 555.0·n?1kcal·mol?1. It is noteworthy in passing that the several points on the left side of Fig. 4 do not vary very smoothly with increasingn, and their tendency to deviate from the fitted equation is even visually detectable,which indicates that the electronic structure of these molecules has not yet reached convergence with respect ton.

The red dots in Fig. 5 present the SE of various cyclocarbons estimated using the fitted equation SE = 555.0·n?1kcal·mol?1given above. It can be seen that ring strain decreases smoothly as the ring size increases,and the experimentally observed cyclo[18]carbon has SE of 61.7 kcal·mol?1.It is worth to note that although the SE of cyclo[18]carbon estimated by the aforementioned homodesmotic reaction is evidently less rigorous, the result at a convergedm(about 59 kcal·mol?1) has a similar magnitude with the regression analysis result. This finding suggests that the homodesmotic reaction method is useful as a crude and rapid estimation of SE for a specific cyclic molecule. Compared to the regression analysis,a key advantage of this method is that it does not require the calculations of a number of large-sized ring systems,and hence the calculation cost is conspicuously cheaper.

Although the expense of the very accurate DLPNOCCSD(T)/cc-pVTZ calculation is affordable for the systems involved in the present study,its cost may be formidably high for significantly larger molecules. So, it is worth to examine if theωB97XD/def2-TZVP level, which is considerably cheaper while can also correctly represent cyclocarbon,is also able to give rise to a reasonable estimation of SE. The blue points in Fig.5 correspond to the SE values derived using the regression analysis based onωB97XD/def2-TZVP electronic energies. The accuracy of the results is seen to be acceptable,if one does not care about 1–2 kcal·mol?1error in SE for a medium-size cyclocarbon.

Fig.5.Strain energy of cyclo[2n]carbon with different n estimated using the fitted relationship based on electronic energies of two different calculation levels.

3.2. Strain energy of boron nitride

The regression analysis method employed in the last section is also applied to boron nitride ring to explore the relationship between SE and number of repeat units, the result is shown in Fig.6.From the figure one can see that the regression analysis works well again, with almost perfectR2(>0.999).The N–B–N and B–N–B angles of the optimized boron nitride rings are also plotted in Fig. 6(b). It is seen that the N–B–N angle almost always keeps linear irrespective of size of the ring,while the B–N–B angle increases smoothly with respect to number of repeat units, and its variation curve looks like mirror inversion of SE curve, suggesting that the bending of the B–N–B angle is mostly responsible for the strain effect of the boron nitride rings.

Fig.6. (a) Energy per repeat unit of BnNn with different n. The red curve portrays the relationship fitted for points of n ≥13. (b) Strain energy of BnNn evaluated using the fitted equation.

By comparing the regression equations in Figs. 5 and 6(b), it is found that the ring strain of BnNnsystems is significantly weaker than that of cyclocarbon systems. For example, SE of B9N9is only 16.1 kcal·mol?1, which is much smaller than that of the cyclo[18]carbon with the same number of repeat units (61.7 kcal·mol?1), what is the reason behind this? The reason of the fairly small SE of the BnNnsystems should come from the fact that the B–N–B angles can bend relatively easily. We anticipate that when the system forms a cyclic structure, the nitrogen atoms could form an sp2-like hybridization state without significant increase in energy. The occurrence of the lone pairs revealed by the electron localization function(ELF)[49–51]in Fig.7 provides a direct evidence of the sp2-like hybridization. In contrast, the N–B–N angles are much more rigid and have a very strong tendency to keep linear status. Even in the smallest boron nitride ring considered in this work(B7N7),the N–B–N angle deviates to linearity merely by 2.3?.

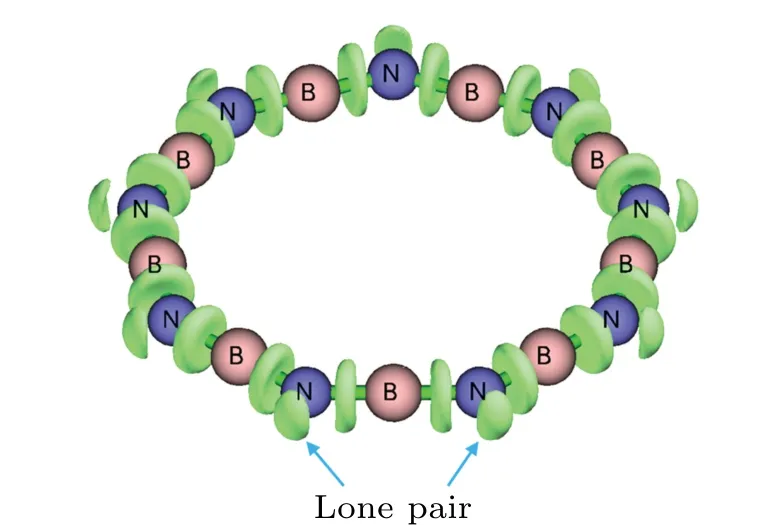
Fig.7. Isosurface of electron localization function of 0.85 a.u. (atomic unit)of B9N9. Wavefunction was generated at ωB97XD/def2-TZVP level.

3.3. Strain energy of cyclic polyacetylene

In this section we study strain effect of c-PA.Before doing this, it is worth to look into its electronic structure first because of its close relationship with ring strain effect. A very useful and intuitive way of revealingπelectron delocalization is localized orbital locator ofπelectrons(LOL-π).[52]The isosurface map of LOL-π=0.4 a.u. plotted by Multiwfn program for [18]c-PA is given in Fig. 8, from which one can clearly find [18]c-PA forms a global in-planeπconjugation.According to the shape of the isosurface, theπinteraction is much stronger over the short C–C bonds than over the long C–C bonds. The existence ofπinteraction can also be well revealed by Laplacian bond order.[53]The values of the short and long C–C bonds are calculated to be 1.71 and 1.35, respectively. Because both of them are evidently larger than 1.0(which corresponds to a typical C–Cσbond),there must be a considerableπcomponent over the bonds, and theπinteraction is distinctly stronger for the short C–C bonds.

We employed the same procedure as the previous sections to calculateE·n?1and fitted the relationship between SE andn, see Fig. 9. It can be seen that the SE of c-PA is slightly larger than that of cyclocarbon with samen,namely SE = 629.8·n?1kcal·mol?1of the formerversusSE=555.0·n?1kcal·mol?1of the latter. The main reason of their comparably large SE should source from the fact that both of them possess analogous in-planeπinteraction between adjacent repeat units,which imposes a strong resistance to the in-plane bending of the angles,as the bending will weaken theπconjugation and thus lead to a great increase in energy. It is noteworthy that although cyclocarbon systems also possess additional out-of-planeπdelocalization over the ring, it has no direct contribution to SE, because forming the cyclic geometry (in other words, in-plane bending the C–C–C angles)does not lead to a notable perturbation on the out-of-planeπconjugation.

Fig. 8. Isosurface map of localized orbital locator of π electrons (LOL-π)of[18]c-PA.Isovalue is chosen to be 0.4 a.u. Lengths of short and long C–C bonds optimized at ωB97XD/def2-TZVP level are labelled.

Fig. 9. (a) Energy per repeat unit of [2n]c-PA with different n. The red curve portrays the relationship fitted for points of n ≥13. (b)Strain energy of c-PA evaluated using the fitted equation.

We noted that the B3LYP exchange–correlation functional[54]in combination with 6-31G(d) basis set[55]was frequently employed in literatures to study SE,[1,7]probably because both the functional and the basis set are very popular, and meantime this level is fairly cheap and thus can be applied to very large systems. Is B3LYP/6-31G(d) really a suitable choice for evaluating SE? Does the more expensiveωB97XD/def2-TZVP level give better result? Since these two questions are important for practical research, we decide to explore them using the c-PA systems with the high quality DLPNO-CCSD(T)/cc-pVTZ data as reference. TheE·n?1calculated for c-PA using the two levels are shown in Fig.10, the employed molecular geometries were also optimized using the corresponding levels. It is found that theE·n?1calculated byωB97XD/def2-TZVP varies smoothly asnincreases like the case of DLPNO-CCSD(T)/cc-pVTZ(Fig. 9) whennis not too small. In contrast, theE·n?1calculated by B3LYP/6-31G(d) shows a sawtooth-like variation withn, which are obviously unreasonable as they show a quite different variation behavior compared to the highprecision DLPNO-CCSD(T)/cc-pVTZ result. As can be seen in Fig. 10, whennchanges from even to odd, which also corresponds to the number ofπelectrons in c-PA changing from satisfying Huckel’s 4neleanti-aromaticity rule to 4nele+2 aromaticity rule,the reduction inE·n?1is extraordinarily remarkable, implying that B3LYP may overestimate the stabilizing effect of aromaticity on the systems. It is noted that some literatures have also reported the inappropriateness of using B3LYP to represent extendedπconjugated systems,[56,57]and it even fully fails to give rise to a qualitatively correct geometry of cyclo[18]carbon.[24]Despite of the problematic representation ofE ·n?1by B3LYP/6-31G(d)and the relatively low fitting quality shown in Fig.10(R2=0.976),the fitted relationship between SE andnis surprisingly satisfactory. The result SE=0.99823·n?1Hartree or 626.4·n?1kcal·mol?1is fairly close to the aforementioned SE = 629.8·n?1kcal·mol?1derived using DLPNOCCSD(T)/cc-pVTZ, and it is even slightly more accurate than the SE = 643.7·n?1kcal·mol?1fitted at the more expensiveωB97XD/def2-TZVP level. However, considering that the seemingly good result of B3LYP/6-31G(d) may largely come from fortuitous error cancellation, it is not recommended by us to evaluate SE of globally conjugated cyclic systems because of its underlying failure in representing theE·n?1, whileωB97XD/def2-TZVP is more worth to recommend since it is more robust and universally applicable.

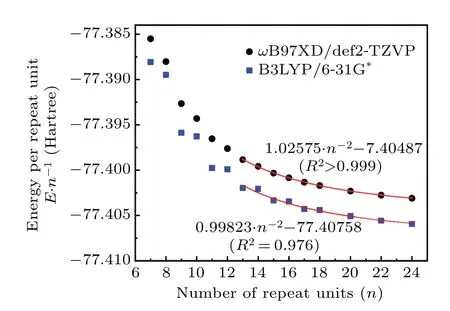
Fig. 10. Energy per repeat unit of [2n]c-PA with different n evaluated at ωB97XD/def2-TZVP and B3LYP/6-31G(d) levels (geometries were also optimized at the corresponding levels). The red curves portray the relationship fitted for points of n ≥13.

4. Summary

In this work, based on very accurate electronic energies evaluated at DLPNO-CCSD(T)/cc-pVTZ level,we conducted systematical research on strain energy (SE) of cyclocarbon,its isoelectronic analogue boron nitride ring, and cyclic polyacetylene(c-PA),which shares similar in-planeπconjugation character with cyclocarbon. The main findings of this work are summarized below.

(i) The general relationship between SE andnof cyclo[2n]carbon, BnNnring, and [2n]c-PA can be successfully built using regression analysis,namely SE=555.0·n?1,145.1·n?1, and 629.8·n?1kcal·mol?1for the three kinds of systems,respectively.

(ii) The harmonic potential of the C–C–C angles in cyclocarbon can be straightforwardly derived using SE data of different ring sizes, and the force constant is found to be 56.23 kcal·mol?1·rad?2.

(iii) The strain effect of BN ring is significantly smaller than that of cyclocarbon due to easily bendable B–N–B angles. c-PA exhibits a similar strength of ring strain with cyclocarbon because both of them possess a comparable in-planeπconjugation character.

(iv) The homodesmotic reaction can also be used to calculate SE of cyclocarbon,and the result does not deviate from regression analysis noticeably. Although this method is obviously less rigorous in principle, it has the advantage that the calculation is much easier and inexpensive.

(v) If DLPNO-CCSD(T)/cc-pVTZ level is too timeconsuming for evaluating the electronic energies of large rings used in regression analysis, thenωB97XD/def2-TZVP is a good alternative. In contrast, the popular and very cheap B3LYP/6-31G(d) level should be used with caution for extended delocalized systems like c-PA.