One-dimensional PT-symmetric acoustic heterostructure

Hai-Xiao Zhang(張海嘯) Wei Xiong(熊威) Ying Cheng(程營) and Xiao-Jun Liu(劉曉峻)

1Department of Physics,MOE Key Laboratory of Modern Acoustics,Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China

2School of Electrical and Information Engineering,Changzhou Institute of Technology,Changzhou 213032,China

3State Key Laboratory of Acoustics,Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China

Keywords: acoustic PT-symmetric heterostructure, anisotropic transmission resonance, occasional bidirectional transmission resonance

1. Introduction

One of the most intriguing developments in quantum mechanics over the past few decades has been the discovery of a non-Hermitian HamiltonianHthat commutes with the parity-time (PT) operator, a property that leads to realenergy eigenvalues.[1–3]Recently, considerable efforts have been further motivated to investigate its classical analogy in photonics,[4–12]acoustics,[13–23]and many more areas[24–27]by means of interleaving balanced loss–gain regions. In contrast to the photonic gain that can be straightforwardly implemented in a locally controlled fashion through stimulated emission, which involves optical (electrical) pumping by an external source or via parametric processes,[28–31]no passive acoustic gain material exists in nature. General physical realizations of acousticPTsymmetry rely on the presence of electromechanical cone loudspeakers,[14–16]forced air flows,[17]or piezoelectric transducers.[19,20]Although the equivalent loss–gain balance can be circumvented by implementing unbalanced loss-only structures,[32,33]the absence of gain gives rise to the intrinsic loss of overall energy. More recently,the implementations of effective acoustic gain through electro-thermoacoustic[34–38]and photo-thermoacoustic[39,40]effects promise versatile routes for the exploration of acousticPTsymmetry.

Up to now,all available designs ofPT-symmetric acoustics are constructed on the basis of balanced gain-loss pair coupled by elaborately configured interlayer, which take advantage of additional coupling mechanism. For example, the unidirectional transmission resonance in Ref. [13] is induced by thePTsymmetry and the Fabry–Perot (FP) resonance of the system.However,the bidirectional transmission resonance in Ref.[21]is the consequence of thePTsymmetry,FP resonance,and periodic structure of the system.Thus,the presence of exceptional points is investigated by varying the distancedbetween the gain and loss components, and their balance is achieved for specific values ofk0d, wherek0stands for the wave number in air. Therefore, the concise heterostructure without interlayer impling entirely disparate physics and design philosophies toPTsymmetry[9]urgently needs to be adequately exploited,according the degree of freedom of acoustic medium, geometry and frequency simultaneously via a generalized theoretical model.

The purpose of this article is to explore the specific properties whenPTsymmetry imposes on the transmission and reflection in arbitrarilyPT-symmetric heterostructure,in both the symmetric and broken-symmetric phases by using an experimental parameter-related transfer matrix in acoustics. We first derive the conservation relations governing the one-dimensional (1D)PT-symmetric acoustic heterostructure, which could be employed to predominantly determine whetherPTsymmetry is achieved in a given physical structure. A set of transmission resonance patterns are demonstrated as a consequence of the derived conservation relations,in which the reflection vanishes only for waves incident from one side of the structure, referred to as anisotropic transmission resonances (ATRs). Last, we demonstrate an occasional bidirectional transmission resonance (OBTR) with bidirectional transparency but vastly different spatial pressure profiles for incidence from opposite sides. The findings may provide substantial support for the development ofPT-symmetric theory and prototype devices with richer acoustic phenomena.

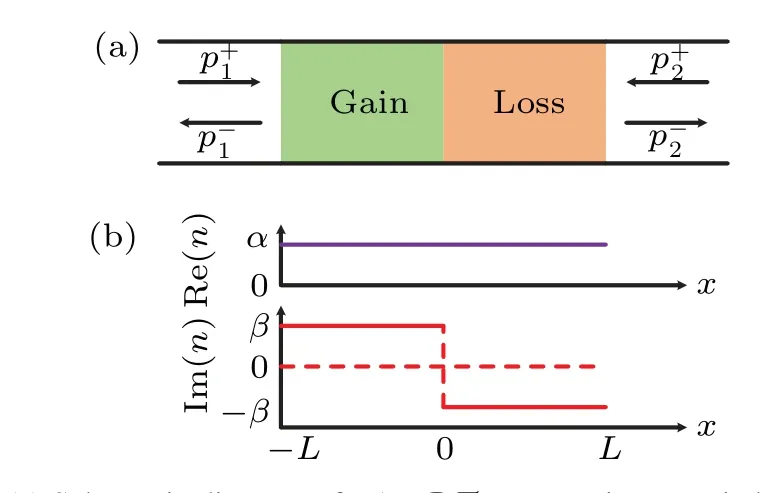
Fig.1. (a)Schematic diagram of a 1D PT-symmetric acoustic heterostructure,constructed by a pair of medium layers that are PT-symmetric about x=0, i.e., n(x)=n?(?x) in panel (b). Green and orange regions indicate gain and loss medium,respectively.

2. Generalized unitary relation

We begin with the scattering matrixSrdefined by[17]

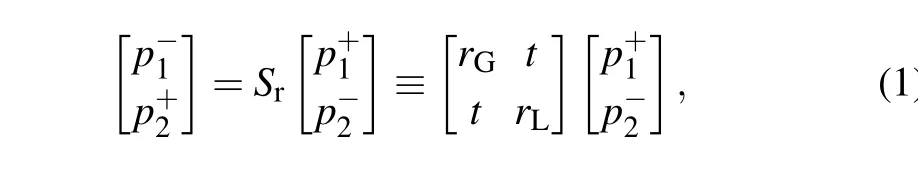
The overall transfer matrixΓ=Γ1Γ2can be obtained,[41]whereΓmis the transfer matrix expressed as

Equations (5) and (6) are valid for all 1D acoustic heterostructures withPTsymmetry as following.

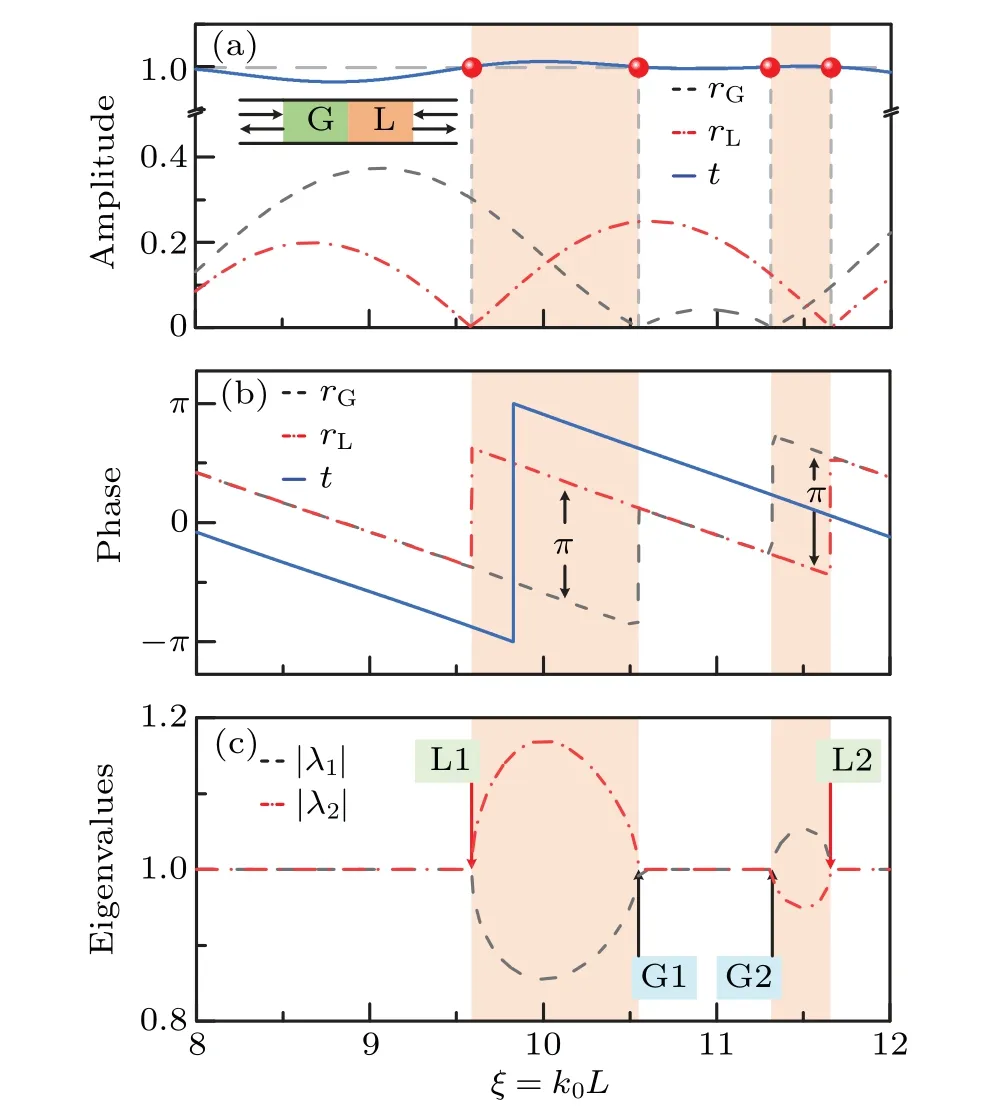
Fig.2. (a)Reflection and transmission spectra of a 1D PT-symmetric heterostructure with index n=0.8±i0.05 and length L. The black dashed,red dashed-dotted, and blue solid curves show |rG|, |rL|, and |t|, respectively. Zeros of the reflections and corresponding anisotropic transmission resonances(|t|=1)are marked by vertical gray dashed lines and red dots.(b) Phases of rG, rL, and t in panel (a), demonstrating the reflection phase jumps at each ATR. (c) Absolute eigenvalues of scattering matrix St. The four resonances marked as modes L1,G1,G2,and L2 from low to high frequency in sequence correspond to the reflection valleys in panel(a)and the phase jump points in panel (b). |λ1| and |λ2| are labeled and indicated by the black dashed and red dashed-dotted curves,respectively. The white and orange backgrounds indicate that the system is in the PT-symmetric phase and broken phase,respectively.

For|t|< 1, we getab> 0 from Eq. (5) and|t|2+|rG||rL| = 1 from Eq. (6). The former refers that?G=?L=?t±π/2, where?G,L,and?tare the phases of reflection and transmission coefficients. The latter is an intriguing generalization of the more familiar conservation relation|t|2+|r|2=1, which applies to a unitary(T-symmetric)matrix for which the left and right reflections (defined asr) are necessarily equal.[42]In thePT-symmetric case,the geometric mean of the two reflectances|rG||rL| replaces the single reflectance|r|2. Therefore, when|t|< 1, the scattering of a single incident wave from one side of the structure is subunitary(some flux is lost)while the scattering from the other side is superunitary(some flux is gained). It should be noted that an accidental degeneracy only appears at|rG|=|rL|, in which case the flux conservation of scattering from both sides cannot be accomplished (δ3/= 0) unless an introducing additional tuning parameter (e.g., the in-between air coupling layer in typicalPT-symmetric setup in Ref.[16]). The above mentioned phenomena are shown by the white background regions in Figs. 2(a) and 2(b), which describe the scattering properties of a 1DPT-symmetric heterostructure with indexn=0.8±i0.05 and lengthL.

In contrast, when|t|> 1, all single-sided scattering processes are superunitary. Thus, we obtainab< 0 from Eq.(5)and the conservation relation of Eq.(6)becomes|t|2?|rG||rL|=1. Similarly,the former indicates that?G??L=πand?G,L=?t±π/2,while the latter describes a class of conservation relations that cannot exist in Hermitian systems. Accidental reflection degeneracies(|rG|=|rL|,requiringδ4=0)are possible in this regime,[42]leading to the usual pseudounitary conservation relation|t|2?|r|2=1, as shown by the orange background in Figs.2(a)and 2(b).

To further explore thePTsymmetry of the structure,we consider the scattering matrix[13]

3. Anisotropic transmission resonance

As noted above,equation(6)implies an considerable interesting phenomenon: there exists a flux-conserving scattering process for incident waves if and only if|t|=1,while only a single one ofrGorrLvanishes. Such process can be referred as an ATR,[9]which is a generalization of the flux-conserving transmission resonances in unitary structures(β=0,|r|=0,and|t|=1)independent of the incidence direction.These ATR modes are marked by red dots in Figs.2(a)and 2(c)as modes L1, G1, G2, and L2 atk0L=9.59, 10.55, 11.32, and 11.66,respectively. It is convenient to distinguish these four modes:(i)Modes G1 and G2 are ATRs at the gain-side reflectionless state(rG=0)corresponding to the gain-side reflection phase jumps,whereas modes L1 and L2 are ATRs at loss-side reflectionless state (rL=0) associated with the loss-side reflection phase jumps. (ii)Modes G1 and L1 arise from a bidirectional transmission resonance(BTR)(β=0,ξ0=μπ/2α,andμis an odd number)of the unitary structure,while modes G2 and L2 arise from the other BTR of the unitary structure (β=0,ξ0=μπ/2α,andμis an even number).

A surprising property of ATRs is that their intensity profile is spatially symmetric. For a spatial profilep(x)of a left-(right-)going transmission resonance,p?(?x)after aPToperation is also a left-(right-)going transmission resonance of the same structure. Since these two states occur at the same frequency,they must be identical(up to a phaseφ)by the requirement of uniqueness:

Hence,the amplitude satisfies|p?(?x)|=|p(x)|. This is consistent with the intuitive expectation that to conserve flux,the acoustic energy must spend an equal amount of time on average in the loss and gain regions of the heterostructure. Except at the ATRs,intensities do exhibit asymmetry for bidirectional incidence,and in particular this is the case for a wave incident from the side with nonvanishing reflection.

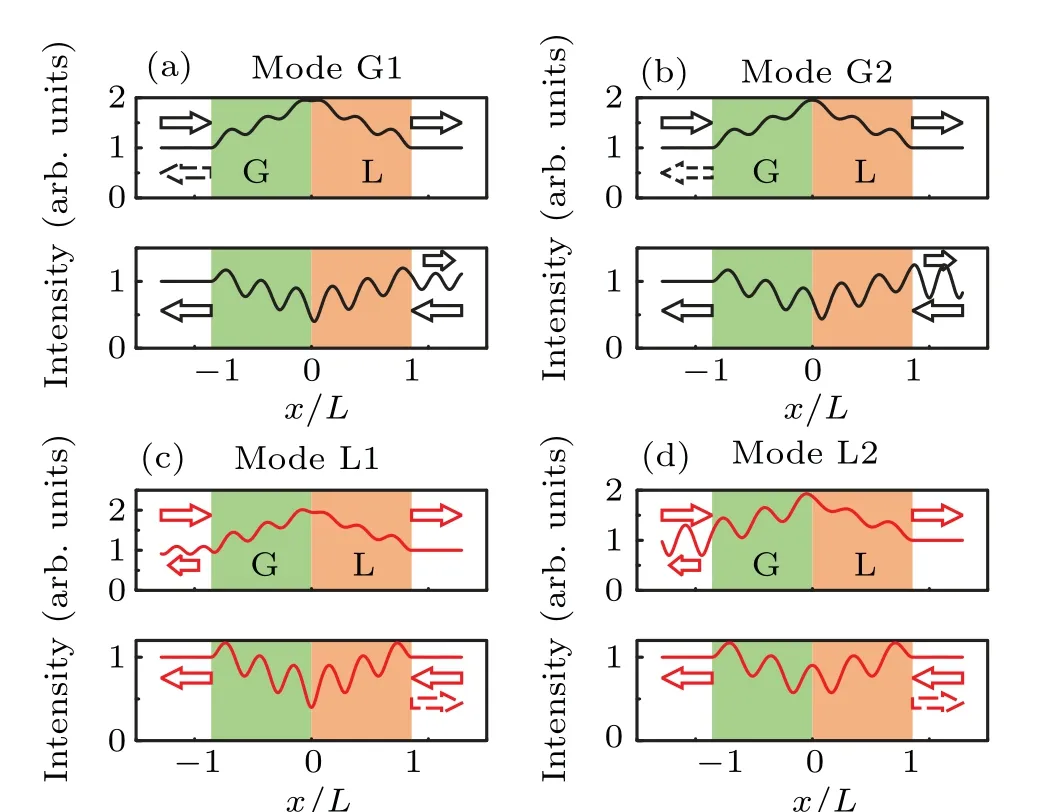
Fig.3. (a)–(b)Spatial profiles of ATR modes G1 and G2,indicating unidirectional reflectionless from the gain side. (c)–(d) Spatial profiles of ATR modes L1 and L2,indicating unidirectional reflectionless from the loss side.The top(bottom)panel shows wave incidence from the gain(loss)side.

The spatial profiles of gain-side invisibilities,corresponding to the aforementioned ATRs of modes G1 and G2, are shown in Figs.3(a)and 3(b).The top panels exhibit the spatial symmetry of their pressure amplitude profile and the bottom panels identify the asymmetry under non-ATR condition. For comparison,figures 3(c)and 3(d)carry out a disparate vision of loss-side invisibilities, associated with the aforementioned ATRs of modes L1 and L2. To our surprise,in modes G1 and L1,the spatial profiles reach minimums at the gain–loss interface,which is consistent with the spatial profile of their corresponding BTR.As expected,modes G2 and L2 have a similar phenomenon, where the spatial profiles reach maximums at the gain-loss interface.

4. Occasional bidirectional transmission resonance

Owing toPTsymmetry,a couple of ATRs therefore arise from the BTR of the unitary structure(β=0),resulting in unidirectional invisibility at different frequencies and incident directions (e.g., modes G1 and L1). Further exploration shows that, there exists a series of occasional bidirectional transmission resonances(OBTRs),which inherit the characteristic scattering properties of the unitary structure at a hand-to-hand frequency, but exhibit obvious differences in the amplitude profiles. The implementation of this phenomenon depends on the precondition ofa=b=0 (δ3=δ4=0), which cannot be demonstrated strictly via the equation evolution. Nevertheless, this phenomenon can still be simulated under approximate conditions: (i)β ?α;(ii)βξ ～0(low normalized frequency); (iii)ξ ～μπ/2α, andμmust be an even number;(iv)β ～0. We illustrate the mathematical and physical mechanisms that underline this phenomenon in detail.

According to the transfer matrix model,provided that the first three conditions are fulfilled, the scattering parameters can be reduced to

It is much more complicated to implement an OBTR in the current case than in the previous case unless 4β/α ～0.

Based on the above four assumptions, we explore the scattering properties and spatial profiles of an OBTR inPTsymmetric heterostructure and its mirrored BTR in a unitary structure. Figures 4(a)–4(c) show the scattering amplitudes,phases, and absolute eigenvalues of thePT-symmetric heterostructure with indexn=1.2±i0.05, while figures 4(d)–4(f) exhibit the corresponding properties of unitary structure with indexn=1.2. Definitely, the OBTR shares an exceptional point (EP) with the initial BTR atξ=2.64 (～π/α),however the scattering behavior near the EP is widely divergent. It is interesting to note that although the bidirectional reflection and transmission coefficients around EP are discrepant,the initial conservation relationship|t|2+|rG||rL|=1 is still maintained, indicating that both structures undergo a symmetric phase [Figs. 4(a) and 4(d)]. This verdict can also be simply caught from the phases of scattering parameters, as shown in Figs. 4(b) and 4(e). Another point worth noting is that when OBTR occurs, the phase of the bidirectional transmission coefficient is?t=0,which has never been demonstrated in a singlePT-symmetric structure but periodic cell units.[43,44]Whereas ATRs achieve unidirectional reflectionless (unitary transmission) in thePT-symmetric heterostructure, OBTR approaches bidirectional invisibility, despite their acoustic pressure amplitude distribution in the gainloss medium being different. Figure 4(c) shows the absolute eigenvalues ofStfor thePT-symmetric structure,and there is a perturbation in the OBTR around the EP,which is consistent with the prediction that the OBTR is an approximate solution.On the contrary, for the unitary structure, the absolute eigenvalues are always one in the whole frequency range,as shown in Fig.4(f).

Figures 4(g) and 4(h) demonstrate the spatial profiles of the EPs of mode “OBTR” in Fig. 4(c) and mode “BTR”in Fig. 4(f), respectively. The results indicate that both thePT-symmetric heterostructure and the unitary structure exhibit unitary transmission at the unidirectional invisibility frequency, regardless of whether the incident wave initially passes through a waveguide with loss or gain. As shown in the top panel of Fig. 4(g), the incident wave with normalized frequencyξ=2.64 passes through the gain portion from the left side, and the amplitude of the acoustic pressure increases to 1.118 (at the gain–loss interface). The amplitude then decreases to 1 in the loss portion. On the other hand, in the bottom panel of Fig. 4(g), the incident wave with identical normalized frequency first passes through the loss portion from the right side, and the amplitude of the acoustic wave decreases to 0.9 (at the loss–gain interface). The amplitude then increases to 1 in the gain portion. The spatially symmetric amplitude of acoustic waves indicates that the energy amplified (absorbed) in the gain (loss) waveguide is completely reproduced in the loss (gain) waveguide at the mirrored position, leading to unitary transmission and reflectionlessness.This is distinct from the manifestation of the initial BTR in a unitary structure,in which the spatial profiles of bidirectional incidence are exactly reciprocal and the intensity at the gain–loss interface is undoubtedly 1[Fig.4(h)].The conclusion further proves that OBTR in aPT-symmetric heterostructure and BTR in unitary structure are two different physical processes,although their scattering matrices are identical,including amplitudes and phases.

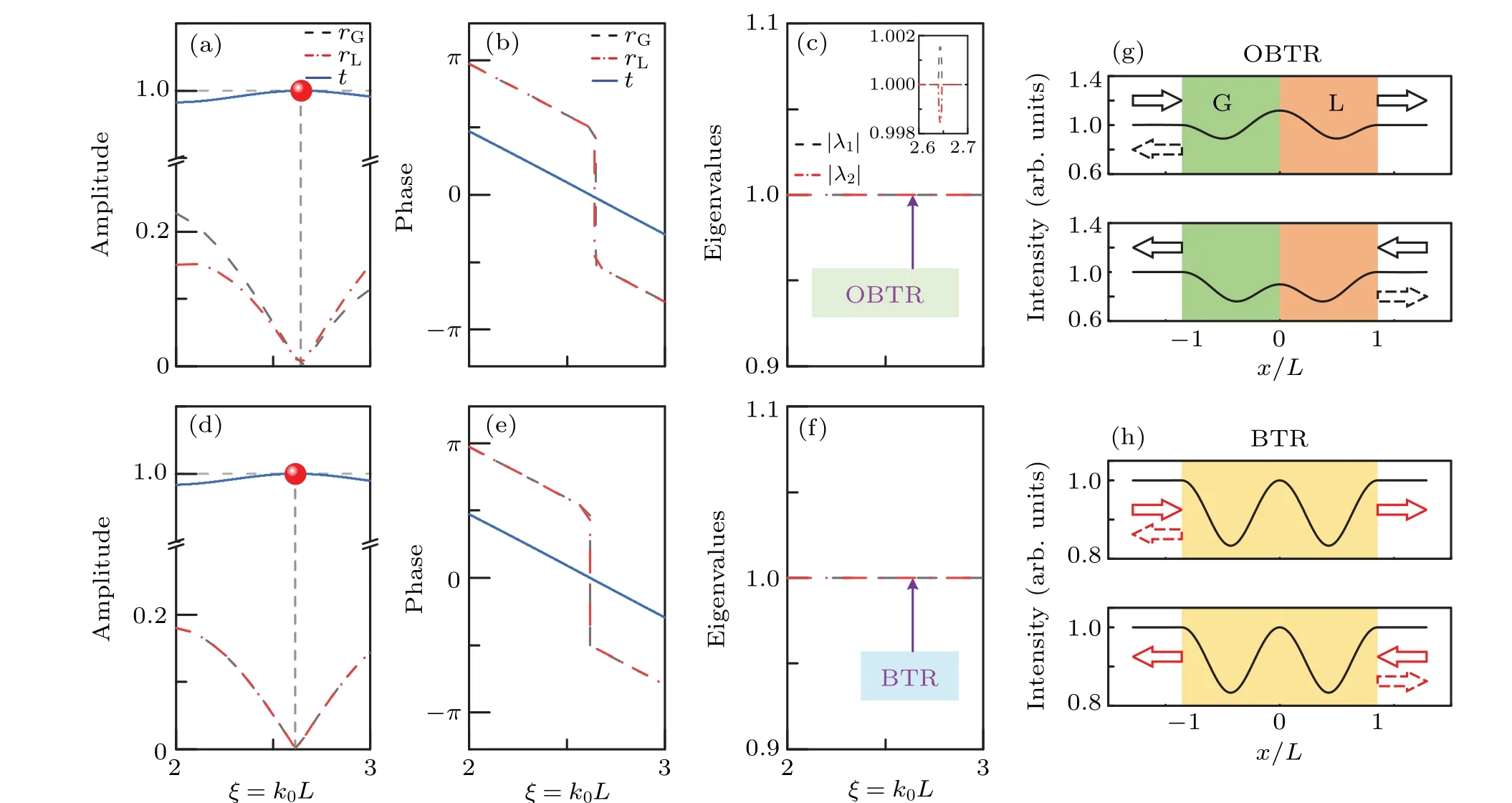
Fig.4. (a)Reflection and transmission spectra of a 1D PT-symmetric heterostructure with index n=1.2±i0.05 and length L. Zero of the reflection corresponding to OBTR are marked by red dots. (b) Phases of rG, rL, and t in panel (a) demonstrate the reflection phase jump at EP. (c) Absolute eigenvalues of scattering matrix λ1,2. The single mode marked as mode“OBTR”corresponds to the reflection valley in panel(a)and the phase jump point in panel(b). Inset:zoomed-in around the OBTR at ξ =2.64. (d)–(f)Same as panels(a)–(c)but for unitary structure with index n=1.2 and length 2L. (g)The unitary nonrecopical transmission resonance of mode“OBTR”labeled in panel(c). (h)The profiles of mode“BTR”labeled in panel(f).

5. Conclusion and discussion

To conclude,we have derived the generalized unitary relation for the scattering matrix of arbitrary 1DPT-symmetric acoustic heterostructure from the transfer matrix, including a conservation relation between the transmission and the gain(loss)side reflection. The conservation relation leads to a simple criterion for identifying the EPs at which thePTsymmetry is spontaneously broken or restored. These EPs are shown to be closely related to thePT-symmetry-breaking transition of the underlying effective Hamiltonian of the structure. In addition,the discovery of four patterns of ATRs has enhanced our physical understanding ofPT-symmetric heterostructure and its scattering EPs. The existence of the OBTR can also provide a theoretical basis for the realization of bidirectional transmission under non-Hermitian conditions and can be used as one of the methods of acoustic gain(loss)discrimination.

In practical realization, both types of components in thePT-symmetric heterostructure can be realized by designing suitable circuits duo to the emergence of the active acoustic metamaterials,[14,16]which manifest the possibility of realizing the metamaterials with the required effective parameters.Our methodology can be applied to relevant fields such as electronics, optics, microwaves, and elastic metamaterials. Especially in recent years,preliminary studies have been made onPTsymmetry in elastic wave system.[45–47]In view of the correlation between elastic and sound waves,elastic metamaterials may also provide potential ideas for experimental realization of acousticPTsymmetry,andvice versa. Our results are useful in predicting the propagation features ofPT-symmetric structures and designing devices of asymmetric responses.

Acknowledgements

Project supported by the National Basic Research Program of China(Grant No.2017YFA0303702)and the National Natural Science Foundation of China (Grant Nos. 12225408,12074183,11922407,11904035,11834008,and 11874215).