基于ADRC的永磁同步電機速度環(huán)控制器設(shè)計方法

陶海莉 高孝君

（1.廣東美的暖通設(shè)備有限公司 佛山 528311；2.佛山鴻威技術(shù)有限公司 佛山 528311）

引言

永磁同步電機具有動態(tài)性能好，效率高等優(yōu)點，在工業(yè)領(lǐng)域、民用領(lǐng)域有著越來越多的應(yīng)用[1]。基于矢量控制方法，將其控制方式等效為直流電機，獲得更好的控制效果和性能。永磁同步電機的控制系統(tǒng)由電流環(huán)和速度環(huán)構(gòu)成，并采用PI控制器結(jié)構(gòu)[2]。PI控制器雖然具有結(jié)構(gòu)簡單，調(diào)試方便等優(yōu)點，但是其本質(zhì)是“基于誤差的反饋來消除誤差”，對于系統(tǒng)的擾動以及模型變化等，其控制性能將受到限制。預(yù)測控制、自適應(yīng)控制等現(xiàn)代控制方法在永磁同步電機控制系統(tǒng)的應(yīng)用受到廣泛的關(guān)注。但是，自適應(yīng)預(yù)測控制算法復(fù)雜，對處理器的性能要求較高；預(yù)測控制算法存在模型預(yù)測精度不高、滾動優(yōu)化策略少、反饋校正方法單調(diào)等問題[3]。

自抗擾控制器（active disturbance rejection controller,ADRC）是一種新型的控制方法。該控制器通過對整個系統(tǒng)的內(nèi)外擾動進行實時估計，并進行動態(tài)補償，結(jié)合設(shè)計合適的控制律，從而使得系統(tǒng)獲得更好的魯棒性和動態(tài)性能[4-7]。雖然自抗擾控制器（ADRC）在永磁同步電機應(yīng)用上存在不少的研究成果[8-12]，但是其控制結(jié)構(gòu)復(fù)雜，參數(shù)整定困難等特點，限制了應(yīng)用范圍。

為了降低自抗擾控制器的設(shè)計難度，本文研究了一種基于ADRC的永磁同步電機速度環(huán)控制器設(shè)計方法。將電機的參數(shù)變化以及內(nèi)外擾動擴張為二階變量，構(gòu)建系統(tǒng)的擴張狀態(tài)觀測器（extended state observer, ESO）。將擾動量前饋補償，使得系統(tǒng)等效為串聯(lián)積分環(huán)節(jié)。基于擾動補償后的系統(tǒng)模型，設(shè)計狀態(tài)誤差反饋控制律（state error feedback control law）。為了提升系統(tǒng)的動態(tài)性能，引入了基于跟蹤微分器（tracking differentiator，TD）的前饋控制器。控制系統(tǒng)的整定參數(shù)依賴于系統(tǒng)轉(zhuǎn)動慣量，本文引入了基于擴張狀態(tài)觀測器的轉(zhuǎn)動慣量辨識方法。

通過MATLABSIMULINK搭建仿真模型和永磁同步電機控制器實驗環(huán)境，驗證控制器設(shè)計方法的有效性，并和PI控制器的矢量控制系統(tǒng)進行對比研究。實驗以及仿真的結(jié)果均表明，ADRC的動態(tài)性能以及抗擾動性能優(yōu)于PI控制器。

1 永磁同步電機動力學模型

基于轉(zhuǎn)子磁鏈定向的矢量控制理論，永磁同步電機在忽略高次諧波影響，并進行同步坐標旋轉(zhuǎn)變換可得電壓-電流方程組如下所示：

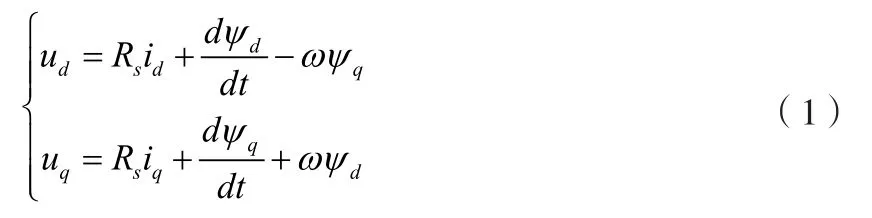
式中：

uq、ud、id、iq—定子側(cè)電壓電流；

Rs—定子電阻；

ω—電氣角速度；

ψd、ψq—磁鏈。

使用d-q電流解耦控制，并基于典I型設(shè)計的電流環(huán)控制器，在考慮控制器以及功率逆變電路上的延時，可以等效為一階慣性環(huán)節(jié)。

式中：

TΣi—電流環(huán)控制器的總延時，包含PWM更新、電流采樣濾波器等；

使用標幺化的運動方程如下所示：

式中：

nN—永磁同步電機的額定轉(zhuǎn)速；

n*—電機轉(zhuǎn)速；

Kt—轉(zhuǎn)矩系數(shù)；

TL—負載轉(zhuǎn)矩；

J—系統(tǒng)的轉(zhuǎn)動慣量；

B—系統(tǒng)粘滯系數(shù)；

2 轉(zhuǎn)速環(huán)自抗擾控制器設(shè)計

由于電流控制帶寬較高，通常采樣PI控制器可以滿足性能要求。速度環(huán)作為外環(huán)，控制帶寬相對較低，且需要面對復(fù)雜的外界工況，結(jié)合自抗擾控制原理，構(gòu)成了如圖1的控制方案。一階自抗擾控制器主要由跟蹤微分器（tracking differentiator，TD）、擴張狀態(tài)觀測器（ESO）以及線性狀態(tài)誤差反饋控制率（state error feedback control law，NLSEF）。自抗擾控制器的跟蹤微分器使系統(tǒng)的過渡過程更加平緩，無超調(diào)。采用擴展狀態(tài)觀測器對系統(tǒng)的擾動及參數(shù)變化進行補償，提升系統(tǒng)的抗擾性能。

圖1 基于ADRC的永磁同步電機速度環(huán)控制框圖

2.1 擴張狀態(tài)觀測器設(shè)計

將式子（3）中的永磁同步電機動力學方程變形成如式子（4）所示。其中a(t)為系統(tǒng)的干擾項，包含了負載轉(zhuǎn)矩以及摩擦力等非線性特性。

將系統(tǒng)擴展成二階，并根據(jù)系統(tǒng)模型設(shè)計擴展觀測器，如下公式（5）所示。

其中b為：

當t→∞時，擴展狀態(tài)觀測器的擴展狀態(tài)z2收斂于如下式所示：

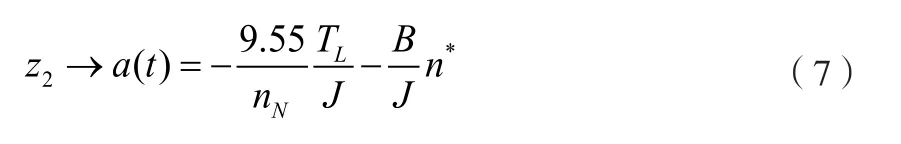
根據(jù)式子（5）所示，擴展狀態(tài)觀測器的輸入值為轉(zhuǎn)速n*和q，輸出值通過狀態(tài)反饋到電流環(huán)的輸入端。

永磁同步電機的電流環(huán)傳遞函數(shù)表達式等效為式（8）所示。

引入擴張狀態(tài)觀測器后，電流環(huán)的控制器輸入將滿足如下關(guān)系是：

電流環(huán)的頻帶寬度遠大于機械環(huán)節(jié)的頻帶寬度。因此在機械環(huán)節(jié)的頻帶寬度內(nèi)，可將電流環(huán)等效為低通濾波器并視為為直通環(huán)節(jié) 結(jié)合式（4）、（8）和（9）表達式，實現(xiàn)對擾動量進行全補償，速度環(huán)的被控對象可以簡化為一階積分環(huán)節(jié)，有助于系統(tǒng)的設(shè)計，提高系統(tǒng)的穩(wěn)定性以及抗擾性能。

使用后向差分方法對轉(zhuǎn)速環(huán)擴張狀態(tài)觀測器進行離散化，有利于在計算機系統(tǒng)上實現(xiàn)。其中h為系統(tǒng)的離散化步長。

對公式（5）進行拉普拉斯變換，并使β1=2ω0，可得式（12）。

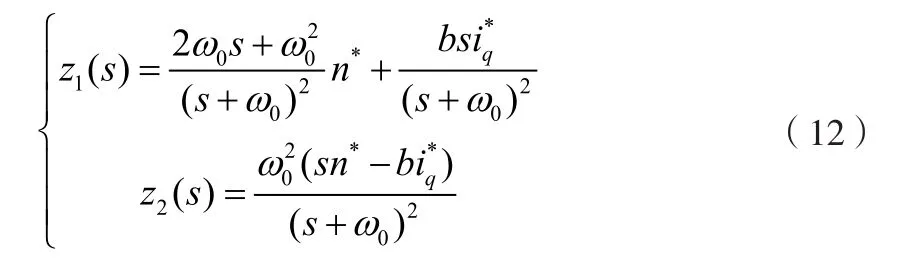
將擴展狀態(tài)觀測器同控制系統(tǒng)結(jié)合后，根據(jù)公式（12）和圖2的結(jié)構(gòu)，系統(tǒng)傳遞函數(shù)模型如圖3所示。其中a(s)為擾動量傳遞函數(shù)表達式。

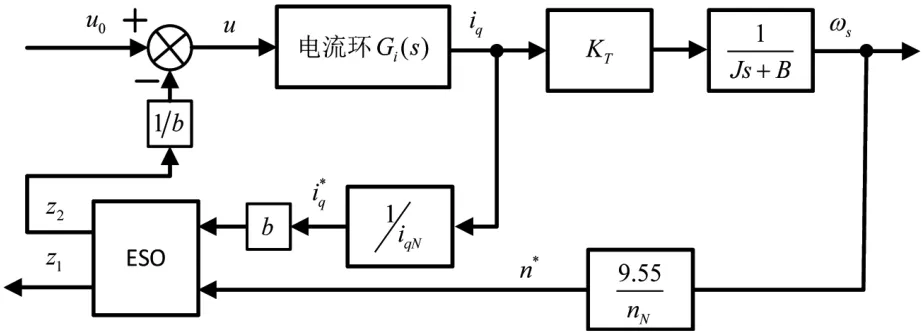
圖2 加入擴張狀態(tài)觀測器的轉(zhuǎn)速環(huán)控制結(jié)構(gòu)圖

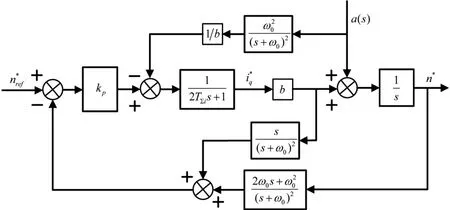
圖3 加入擴張狀態(tài)觀測器后的擾動模型

根據(jù)系統(tǒng)框圖，可得擾動量通道的傳遞函數(shù)表達式為：

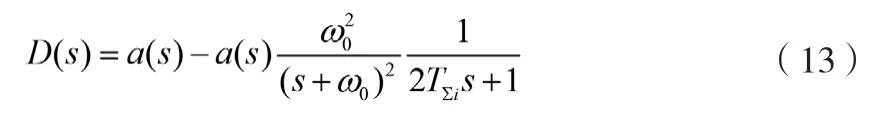
當擾動信號為階躍信號時，式（13）的總擾動量將接近0，如式（14）所示。

當擾動信號為斜坡信號時，系統(tǒng)的總擾動量將存在一個靜態(tài)的誤差值。

不引入擴展狀態(tài)觀測器時，系統(tǒng)的穩(wěn)態(tài)誤差為：

將擴張狀態(tài)觀測器設(shè)計成二階共零點的形式，將保證系統(tǒng)的快速性和穩(wěn)定性。并能夠?qū)τ陔A躍信號擾動保持無靜差跟蹤。根據(jù)以上設(shè)計，提升了系統(tǒng)的抗擾動性能。

2.2 控制器設(shè)計

根據(jù)“分離原理”，速度環(huán)控制器和擴展觀測器單獨設(shè)計，就能夠滿足系統(tǒng)的穩(wěn)定性需求，不存在相互耦合的關(guān)系。

（1）線性狀態(tài)反饋控制律

將電流環(huán)等效成一階慣性環(huán)節(jié)，控制環(huán)路結(jié)構(gòu)簡圖如圖4所示。

圖4 轉(zhuǎn)速環(huán)控制結(jié)構(gòu)簡圖

其中反饋回路上的濾波器為：

式中：

Tfn—轉(zhuǎn)速反饋環(huán)路等效延時。

將永磁同步電機的速度環(huán)為二階系統(tǒng)，將其控制器設(shè)計為典II型。在設(shè)計速度環(huán)控制器過程中，將系統(tǒng)等效成單位反饋，把控制系統(tǒng)的濾波器提入到前向通道中，如圖5所示。將電流環(huán)等效閉環(huán)傳遞函數(shù)同低通濾波器環(huán)節(jié)合并，合并后的時間常數(shù)為：

圖5 轉(zhuǎn)速環(huán)控制框圖等效變換

速度環(huán)控制器的線性反饋率的傳遞函數(shù)如下式所示：

式中：

Kn—比例系數(shù)；

τn為積分時間常數(shù)。

因圖5的中開環(huán)傳遞函數(shù)表達式為：

從公式（18）、（19）、（20）中對比可知，基于線性狀態(tài)反饋控制率的速度環(huán)參數(shù)如式（22）、（23）所示：

2.3 TD跟蹤微分器

引入前饋系統(tǒng)，可以提升系統(tǒng)的動態(tài)響應(yīng)性能，拓寬頻帶寬度。根據(jù)圖4控制系統(tǒng)框圖，系統(tǒng)前饋表達式如公式（24）所示：

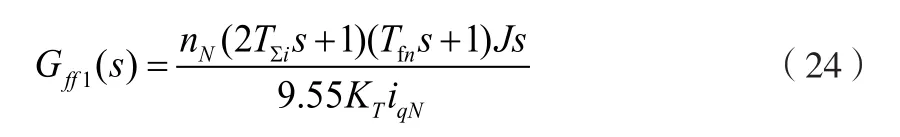
上式（24）是無法通過物理實現(xiàn)分子的階次高于分母的控制系統(tǒng)。雖然可以通過引入三階小慣性環(huán)節(jié)，讓系統(tǒng)變?yōu)榭蓪崿F(xiàn)系統(tǒng)，但是引入速度的三階導(dǎo)數(shù)將帶來大量的高頻干擾，影響系統(tǒng)控制精度，增加系統(tǒng)的損耗。通過忽略高次項，引入一個可調(diào)系數(shù)kff，增加系統(tǒng)的可靠性和穩(wěn)定性，可以控制系統(tǒng)的系統(tǒng)簡化為：

當系統(tǒng)存在模型不準確時，可以通過可調(diào)系數(shù)kff使得控制器達到最佳的控制效果，實現(xiàn)系統(tǒng)的部分動態(tài)補償。

系統(tǒng)模型中存在微分項目，使用跟蹤微分器（TD）代替微分項，更加快速跟蹤微分信號，減少相位滯后，提升噪聲抑制能力。

2.4 總結(jié)

速度環(huán)控制器的結(jié)構(gòu)如圖6所示，使用ADRC的控制器，提升系統(tǒng)的快速性。

圖6 轉(zhuǎn)速環(huán)控制結(jié)構(gòu)框圖

3 基于擴展狀態(tài)觀測器的轉(zhuǎn)動慣量辨識

永磁同步電機的速度環(huán)控制器設(shè)計過程中，都包含轉(zhuǎn)動慣量參數(shù)。在實際應(yīng)用過程中，不同的負載將引起轉(zhuǎn)動慣量變化，進而導(dǎo)致控制對象的變化。引起系統(tǒng)的控制性能下降等。考慮轉(zhuǎn)動慣量的變化量?J，對公式（3）和公式（7）進行重寫，

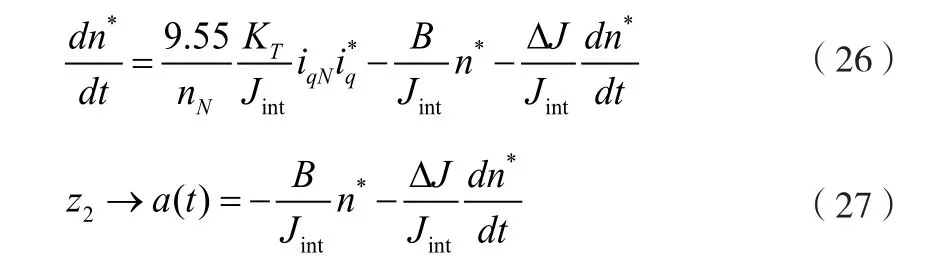
根據(jù)式（24）、（25）可知，給定一個轉(zhuǎn)動慣量的初值Jint，并使負載轉(zhuǎn)矩TL=0，線性擴展狀態(tài)觀測器輸出值，將包含轉(zhuǎn)動慣量變化值。

通過輸入給定的三角波信號源，系統(tǒng)的擴張狀態(tài)觀測器z2的輸出如式（27）所示，輸出值和轉(zhuǎn)速存在一定的關(guān)系。在實際工程中，電機的摩擦系數(shù)相對較小。因此摩擦力等非線性力矩，可以忽略不計。對半個周期內(nèi)的z2進行積分并計算平均值，如式（28）、（29）所示：

將式（28）和式（29）作差，可得：

在給定的三角波信號源中dn*dt的斜率是已知量，對式（30）進行求解，可得：

4 仿真與分析

本文所使用的永磁同步電機的參數(shù)如表1所示。

表1 電機參數(shù)

根據(jù)電機參數(shù)，設(shè)計電機的轉(zhuǎn)速環(huán)以及擴展狀態(tài)觀測器的參數(shù)。并基于此，搭建系統(tǒng)的仿真框圖，如圖7所示。

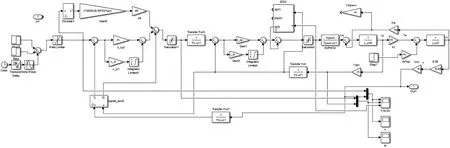
圖7 轉(zhuǎn)速環(huán)傳遞函數(shù)仿真模型

仿真結(jié)果如圖8所示，使用傳統(tǒng)PI控制器，在相同的上升時間，基于自抗擾控制器的速度環(huán)控制器性能優(yōu)于PI控制器，具有更小的超調(diào)量，更強的抗擾動性能。

圖8 速度環(huán)性能仿真對比圖

實驗電機，加入對拖電機后，轉(zhuǎn)動慣量將發(fā)生變化。在仿真系統(tǒng)中，加入轉(zhuǎn)動慣量變化量，輸入轉(zhuǎn)速激勵信號，擴展狀態(tài)觀測器的輸出波形如同圖9（b）所示。最終轉(zhuǎn)動慣量收斂于有真實值。

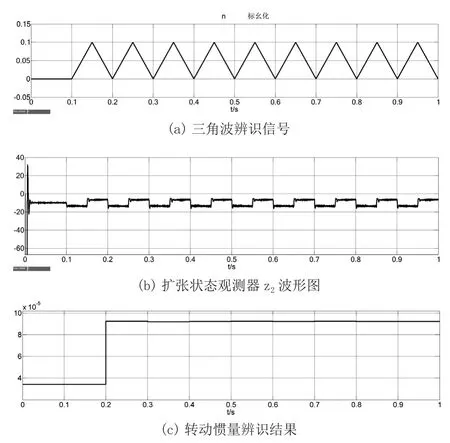
圖9 轉(zhuǎn)動慣量辨識仿真波形圖

5 實驗

本文所使用的實驗平臺如圖10所示。該實驗平臺包含永磁同步電機及其控制系統(tǒng)以及簡易的對拖平臺，被拖動電機為安川400 W電機及其驅(qū)動器，并使用自研的開發(fā)的上位機獲取實驗波形圖。

圖10 永磁同步電機控制系統(tǒng)實驗平臺

實驗平臺上，速度環(huán)的慣量包含了實驗電機、聯(lián)軸器以及對拖電機的轉(zhuǎn)動慣量。速度環(huán)控制器設(shè)計時，需要考慮以上全部慣量值。因此，使用本文提出的轉(zhuǎn)動慣量辨識方法，實驗波形如圖11所示。

圖11 轉(zhuǎn)動慣量辨識實驗波形圖

傳統(tǒng)PI控制器的實驗結(jié)果如圖12（a）所示。啟動過程中，系統(tǒng)存在超調(diào)量，并且恢復(fù)時間更長。在突加負載實驗時，PI控制器的最大調(diào)節(jié)量為3.14 %，轉(zhuǎn)矩變換的時間響應(yīng)為2.42 ms；自抗擾控制器的最大調(diào)節(jié)時間為2.23 %，轉(zhuǎn)矩變換的時間響應(yīng)為1.37 ms，控制系統(tǒng)有更強的抗擾性能。

圖12 速度環(huán)控制器實驗波形圖

6 結(jié)論

本文從理論出發(fā)，通過分析自抗擾控制器的傳遞函數(shù)以及永磁同步電機速度環(huán)的數(shù)學模型，得到了永磁同步電機擴張狀態(tài)觀測器、反饋控制律以及TD微分器的設(shè)計方法。通過仿真與實驗，驗證了設(shè)計方法的有效性和可靠性。通過對比驗證，基于ADRC的永磁同步電機速度環(huán)控制器，具有更快的響應(yīng)性能，更強的抗擾動性能。