二級EMI濾波器磁場近場耦合效應研究

楊湘木 王 會

（珠海格力電器股份有限公司 珠海 519070）

引言

電源EMI（Electromagnetic Interference，電磁干擾）濾波器是抑制傳導電磁干擾常用手段之一。然而，實測電源EMI濾波器，性能與理論預期相差甚遠，造成這種情況的主要原因有：濾波器件的寄生參數，如電容器的引線電感或者電感器的繞組自電容等；印制電路板（PCB）形式的EMI濾波器，板子走線本身的高頻寄生效應[1]； 最后，濾波器布局緊密，器件之間不可避免的存在著較大的近場耦合效應的影響，電磁耦合現象也將影響濾波器的高頻性能。綜上，為了更準確的評估和預測電源EMI濾波器在150 kHz～30 MHz頻率范圍內抑制傳導電磁噪聲的能力，有必要將以上影響因素考慮進設計之中[2]。

目前，對于濾波器的研究主要集中在對關鍵器件的高頻寄生效應研究上，通過提高器件的高頻性能來改善電源EMI濾波器的插入損耗[3]。面向器件之間耦合效應影響的研究相對較少，且大都是基于電路理論，耦合系數的選取具有經驗性、主觀性，無法全面表征材料磁導率、磁飽和特性、線圈形狀尺寸、線圈位置和距離等因素的綜合影響[4]。

本文以二級EMI濾波電路為例，系統研究了器件間近場耦合效應的機理，建立了器件之間耦合的高頻模型，并通過分析器件之間近場耦合量的分布，將器件之間的耦合關系和相互影響通過添加互感系數的方式與整個濾波電路相結合，建立了考慮器件間近場耦合效應的仿真電路模型，避開了人工解耦的繁雜。最后，通過將濾波器插入損耗的仿真計算結果與測試結果相對比，表明近場耦合效應對濾波器性能影響顯著，同時驗證了本文近場耦合建模方法的正確性和可行性。

1 電源EMI濾波器近場耦合的基本原理

1.1 激勵電流下近場耦合分析

近場耦合效應可以在相鄰元器件上產生感應電壓，此感應電壓產生的感應電流可以通過傳導的方式直接耦合到臨近器件，而且，這部分噪聲電流的頻率范圍通常在150 KHz～30 MHz內，因此，傳導干擾預測模型需要將近場耦合的影響考慮進去。

近場耦合包括磁場耦合和電場耦合。研究表明，對于濾波器件間的近場耦合作用，磁場耦合比電場耦合的影響更為嚴重[5]；并且，在實際使用中，用來描述電場耦合作用的等效電容比濾波電感器件自身的寄生電容要小很多[6]，所以，電場耦合效應對濾波性能的影響可以忽略，對于EMI濾波器的近場耦合分析以磁場耦合為主。磁場耦合指的是磁性元件產生的磁場可以在周圍閉合導體上產生感應電壓，此感應電壓產生的感應電流可以通過傳導的方式直接耦合到臨近器件。

本文研究的單相電源EMI濾波器的結構和電路形式如圖1所示，該濾波器為二級濾波，其中，主要濾波元器件有共模扼流圈、跨接于零火線間的X電容和零火線與地之間的Y電容。

圖1 二級電源EMI濾波器

當共模電流流經扼流圈時，由于扼流圈的共模分量較大，共模分量的磁通在磁芯中形成回路，且Y電容的容值一般較小，因而扼流圈與Y電容之間的近場耦合效應可以忽略不計[7]，僅需考慮兩個扼流圈之間的近場耦合效應；當差模電流流經扼流圈時，磁路無法通過環形磁芯閉合，部分磁通通過周邊的空氣形成回路，即產生了漏磁通，且X電容的容值一般較大，因而此時除了扼流圈之間存在耦合作用外，扼流圈與X電容之間的近場耦合效應也將會影響電源EMI濾波器的性能，在實際應用中必須予以考慮。

器件之間存在的耦合特性在電路模型上可以用元件間的互感參數M來表示。綜上，該二級濾波器考慮近場耦合的電路模型如圖2所示。X電容與不相鄰扼流圈之間距離較遠，且有其他器件相隔，二者之間的耦合作用非常弱，為方便分析，在此忽略。

圖2 二階濾波器近場耦合示意圖

1.2 近場耦合電路解耦

互感M存在于兩個元件之間，要分別對它們進行直接測量是不可能的。倘若對包含兩個元件的網絡進行測量，然后從測量的網絡參數數據中推導互感則是可行的[9]。如圖3將X電容與電感解耦模型等效為一個T型網絡，首先測量端口1和端口2的S參數，根據阻抗參數（Z參數）和散射參數（S參數）的變換關系，由測量的S參數計算出電容器支路的阻抗Z3，最終確定M。進一步的，根據表達式（5）求出互感系數K：

圖3 基于S參數解耦示意

其中，為參考阻抗值，一般為50 Ω。

2 電源EMI濾波器的電磁計算模型

2.1 近場磁耦合系數提取

2.1.1 共模扼流圈三維模型的建立

電源EMI濾波器中主要的磁場源是共模扼流圈，首先需要建立扼流圈的三維模型。在以往的設計經驗中，可以通過直接建模，優點是模型能夠最大程度的反應扼流圈螺旋繞多匝漆包線的特征信息，計算精度高，缺點是受限于扼流圈本身的結構特征，直接建模過于復雜，耗時耗力，且由于扼流圈繞組至少幾十匝，導線相對較細，導致有限元網格數量太多，一般不適用于長期的工程應用；另外，對扼流圈還可以簡化建模，主要手段是將多匝線圈合并為完整的幾何結構處理，見圖4。“線包”的處理方式雖然能夠節省建模的難度，并可大大降低電磁仿真計算的要求，但簡化的“線包”模型卻往往不能正確的反應扼流圈的漏磁通影響，由此帶來的誤差很大。

圖4 扼流圈模型的簡化處理

本文中，扼流圈模型的建立采用PEmag軟件包，從軟件自帶的模型庫中取出需要的磁芯形狀及繞組形式等信息來完成二維建模，如圖5所示，陰影部分代表磁芯，綠色部分代表隔離層。本文研究的扼流圈的具體參數見表1，最后根據磁芯的磁化曲線（如圖6）對磁芯材料進行編輯。

圖5 扼流圈二維模型

圖6 磁芯磁化曲線

表1 扼流圈參數信息表

自動生成的扼流圈三維模型如圖7所示。可以看出，Pemag已將扼流圈兩個繞組的螺旋線結構簡化為相同圈數的單匝閉合線圈，兩組繞組在磁芯上形成的包圍角度一致。這種處理方式就能夠真實反映扼流圈漏磁通的情況，保證了仿真的精度，同時使擁有復雜幾何結構的扼流圈模型建立得以簡化。

圖7 扼流圈三維模型

2.1.2 扼流圈之間的互感計算

在Maxwell 3D中建立兩個扼流圈之間的近場耦合模型見圖8所示，將兩個扼流圈分別命名為group1、group2，通過調節激勵方向，分別完成二者之間差模、共模兩種形式的近場耦合量的計算。

圖8 兩個扼流圈互感仿真模型

計算結果如圖9所示。可以看出，差模電流激勵下，兩個器件之間的互感量M=-2401.15 nH；共模電流激勵下，兩個器件之間的互感量為M=-29.76 nH。計算結果中的正、負號分別代表正耦合和負耦合的情況。

圖9 Maxwell中兩個扼流圈互感計算結果

可以看出，共模激勵下扼流圈之間的互感量相對于其自身的磁場特性來說很小，因此不會對實際濾波性能產生影響，為方便計算，共模激勵下扼流圈之間的磁場耦合效應無需考慮。綜上，在建立電源EMI濾波器性能預測模型時，只需要考慮差模模式下磁場耦合效應的影響。本文接下來基于差模濾波特性做進一步分析驗證。

2.1.3 扼流圈與X電容之間的互感計算

當電容器的擺放位置與扼流圈位置較近，電容器的寄生電感就會不可避免的耦合到扼流圈磁芯產生的漏磁場，從而影響其濾波性能。圖10所示是X電容的結構特征，實際能匝鏈外部磁場的面積僅僅是極板底部與引腳之間構成的環路，用陰影表示。這是因為，X電容內部為圈繞結構，鋁箔或銀箔分層交替連接電容兩級，當漏磁方向與電容內部電場方向共面時，該圈繞結構并不在兩極產生電壓；當漏磁方向與電容內部電場方向垂直時，每層金屬箔內部產生環流，也不在兩極感應電壓。因此對該部分模型建立時用等尺寸的金屬塊簡化代替。

圖10 X電容幾何結構

按照電容器結構特性建立如圖11所示的簡化電磁模型，扼流圈與電容器之間相距14 mm。扼流圈繞組和電容器中加入相同的差模電流激勵，并分別命名為group1和current1。完成扼流圈與X電容之間差模激勵下磁場近場耦合計算，如圖12所示，兩個器件之間的互感量為M=25.8 nH。

圖11 扼流圈與X電容互感仿真模型

圖12 扼流圈與X電容互感計算結果

2.2 濾波元件電路模型參數提取

對于濾波元器件的高頻模型，可以基于實驗測量的方法，根據阻抗分析儀的測試結果，結合相應等效電路模型進行參數擬合來建立。

電容器的等效電路模型可簡化為RLC串聯網絡，如圖13所示：ESL為電容器等效串聯電感，它包括電容器的繞線電感、內部引線電感和導線電感；ESR為等效串聯電阻。最終，得到電容的等效電路參數見表2。

圖13 X/Y電容等效電路模型

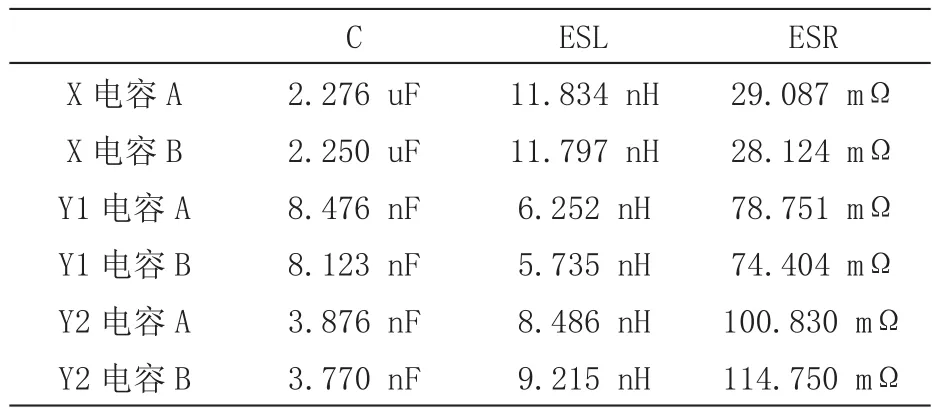
表2 電容模型參數

共模扼流圈的等效差模模型需要考慮線圈的差模電感、繞組交流電阻、電感磁滯和渦流損耗、兩個繞組間的寄生電容以及匝間電容，分別以Ld、Rac、Rd、C2、Cd表示。本文研究的電源濾波器工作電流在20～25 A，選用較粗的線徑（1.6 mm）繞制扼流圈，表面積較大，且出于散熱考慮，導線間距在0.5 mm以上，因此繞組銅線由于趨膚效應和臨近效應導致的交流電阻Rac很小，與感抗相比可忽略不計，最終建立其差模等效電路模型如圖14所示，等效電路參數見表3。

圖14 共模扼流圈差模等效電路模型

表3 共模扼流圈模型參數

因此，根據公式（5），扼流圈之間互感系數K=-0.266；扼流圈與相鄰X電容之間互感系數K=0.08。

2.3 PCB寄生參數提取

電源EMI濾波器的PCB的寄生參數在高頻時對濾波器性能有很大影響，本文通過Q3D Extractor對PCB寄生參數進行數值分析。圖15為由參數提取結果導出的PCB的部分元（PEEC）等效模型，該模型用來反映PCB板布局布線等因素的影響。

圖15 PCB寄生參數的PEEC模型

3 仿真與實驗驗證

3.1 器件間近場耦合量計算方法的驗證

為驗證器件間近場耦合效應電磁計算模型的正確性，本文將濾波器中共模扼流圈和X電容的等效電路模型、元器間近場耦合系數以及PCB寄生參數模型，按照圖16所示的電路結構連接起來，元器件間的近場耦合作用已經通過耦合系數K加載到電路之中，對其端口S參數進行計算，源端和負載端阻抗均為50 ?。

圖16 差模仿真電路模型

利用矢量網絡分析儀測試該結構差模端口下的S參數，如圖17所示。將測試曲線與本文模型進行對比，結果如圖18所示。其中，實線代表實際測量得到的曲線，點線代表未考慮元器件間近場耦合效應的差模仿真曲線，長虛線代表考慮近場耦合效應的差模仿真曲線。通過與測試曲線對比，可以看出，考慮近場耦合效應后的求解結果與實測結果接近，證明本文提出的器件間近場耦合量的計算方法正確可行；同時三條曲線對比后也能看出，考慮器件間近場耦合效應在該結構S參數分析中是非常有必要的。

圖17 扼流圈與X電容濾波結構S參數測試

圖18 計算和實測結果

3.2 電源濾波器差模濾波性能驗證

對于圖1中的典型二級EMI濾波器，為了預測差模插入濾波性能，按照上文分析方法將關鍵濾波器件等效電路模型、元器間近場耦合系數以及PCB寄生參數模型搭建完整的電源濾波器差模模型如圖19所示，并使用矢量網絡分析儀對濾波器測試其端口的差模傳輸特性，源端和負載端阻抗設置為50 ?，最終結果如圖20所示。實線是實測結果，長虛線是考慮近場耦合效應計算結果，點線是未考慮近場耦合效應計算結果。對比可知，在整個傳導干擾測量范圍內150 kHz～30 MHz，近場耦合效應對濾波器差模衰減性能影響非常大，尤其是在1 MHz之前的低頻段，由于耦合引起了諧振效應，由此可見分析近場耦合作用是預測濾波性能的關鍵工作。最后，應用本文提出的方法考慮器件間近場耦合效應后，仿真得到的電源EMI濾波器差模插入損耗與測量結果吻合良好，使得差模插入損耗預測精度提高了約20 dB。

圖19 EMI濾波器差模仿真電路

圖20 濾波器差模計算與實測結果

4 結論

本文深入研究了二級EMI濾波器，通過對磁性器件精確建模，分析其磁場近場耦合效應機理；最終在提取PCB寄生參數及元器件高頻等效電路模型的基礎上，建立了考慮器件之間近場耦合效應的電源EMI濾波器性能預測模型，通過將計算結果與實測結果比較，驗證了該電路模型的正確性與有效性，從而為電源EMI濾波器對電子設備傳導干擾影響的深入研究奠定了基礎。