液態金屬磁流體發電通道特性分析

李永國， 朱秋瑩， 覃 燦， 李祥燕

（1.上海海洋大學 工程學院， 上海 201306； 2.上海海洋可再生能源工程技術研究中心， 上海 201306）

0 引言

隨著我國對可再生能源的開發和利用，波浪能受到了國內外學者的高度關注[1]。 從最初的旋轉式發電機到直驅式發電機，再到液態金屬磁流體 （Liquid Metal Magnetohydrodynamic，LMMHD）直驅式發電機，新的發電機的研究一步步改進了波浪能發電裝置的不足之處。 與傳統波浪能發電裝置相比，直驅式波浪能發電裝置可以直接將波浪能轉化為電能，省去了中間轉化裝置，結構更簡單，波浪能轉化效率更高。 相比于常規的線圈直驅式發電機，液態金屬磁流體發電機是利用導電液體來切割磁感線，當液態金屬流經發電通道時， 鑲嵌在通道兩側的電極上會產生感應電動勢。 液態金屬磁流體發電機具有發電功率高、結構簡單、成本低等優點。 因此，近年來液態金屬磁流體發電機被廣泛應用在波浪能發電裝置研究中。

國外研究磁流體發電的國家主要有美國、俄羅斯、日本等。 Satake S[2]對帶有磁流體（MHD）發電機的自由活塞內燃機進行了研究，并分析計算了液態金屬磁流體的動力學特性。Niwa N[3]研究了具有非對稱方型截面、對稱方型截面、圓形截面的磁流體發電機，發現非對稱方型截面的發電機具有最高的輸出功率。 Yamada K[4]對液態金屬磁流體發電機進行三維數值分析， 闡明了MHD 發電機中電磁場和流體流動的三維結構。Hu L[5]分析了液態金屬磁流體發電系統在汞、U-alloy47 和NaK78 等3 種不同工作流體下的發電性能， 分析結果表明， 具有低密度和高導電性能的液態金屬可以有效提高發電效率。

我國也非常重視對磁流體發電技術的研究。喬凱[6]將LMMHD 與震蕩水翼捕能技術結合，基于Fluent 軟件對發電通道的特性進行分析， 分析結果表明：高寬比越小，端部效應的作用越明顯；電極過長或過寬都會降低發電效果。易仁義[7]研究了相關參數對液態金屬發電機輸出特性的影響，研究結果表明，空載電壓與入口速度、磁感應強度、發電通道寬度成正比，但是發電通道寬度越大，空載電壓的相對誤差就越大。程邦勤[8]對磁流體發電通道進行了數值模擬研究，研究結果表明：增大磁感應強度或電導率可以增加能量的提取率。 趙凌志[9]利用建立的等效電路模型計算了LMMHD 發電機試驗樣機的輸出特性。 張宇磊[10]建立三維矩形截面發電通道模型對LMMHD 發電進行數值模擬分析，分析結果表明：改變發電通道的參數會導致電磁效率和端部效應程度等發生明顯的變化；若保持通道寬度和相互作用參數不變， 則電磁效率和端部效應程度等也基本保持不變。

國內外學者對液態金屬磁流體發電技術進行了許多研究，但是，對于通道參數對液態金屬磁流體發電性能影響的研究還不夠深入，對于液態金屬磁流體發電技術在工程中的應用還缺乏一定的理論數據支撐。 因此，本文通過數值模擬的方式對發電通道參數對液態金屬磁流體發電性能的影響進行研究，從而為發電通道參數的選取提供理論基礎。

1 液態金屬磁流體發電理論

液態金屬磁流體發電機是基于法拉第電磁感應原理建立的。 當導電液態金屬垂直流經磁場，流體切割磁力線從而產生感應電動勢[11]。 在通道的內側裝上正負電極，當接通外接負載時，導電流體產生的能量便可以直接轉換成電能輸出。

液態金屬磁流體發電通常采用具有高電導率、低熔點的液態金屬作為發電工質。常見的液體金屬有鎵銦錫合金、鈉鉀合金和汞，其主要物理性質如表1 所示[12]。 鎵銦錫合金作為導電液態金屬時，其發電性能要優于鈉鉀合金和汞，故本文選取鎵銦錫合金作為磁流體發電介質[10]。

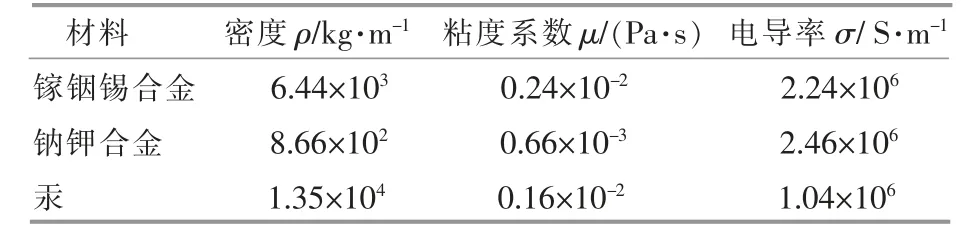
表1 液態金屬的物理性質Table 1 Physical properties of liquid metal

圖1 為液態金屬磁流體發電通道的計算模型（通道寬度為d、高度為h、長度為L）。導電液態金屬以速度v 沿z 軸負方向流進磁流體發電通道內部，磁場方向與流體方向垂直且與y 軸方向相同。在理想條件下，假設電磁場和流場以均勻分布的形式存在于空間中，不考慮誘導磁場的影響，在兩個電極壁面加載負載R 后，可推導出液態金屬磁流體的穩態發電性能參數如下所示[13]。

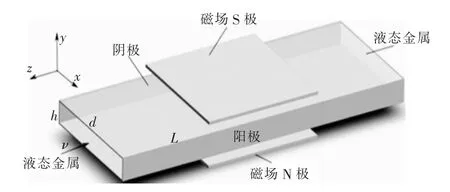
圖1 液態金屬發電通道模型Fig.1 liquid metal power generation channel model

通道內阻r：

2 磁流體發電通道數值模擬討論分析

本文利用Fluent 軟件下的MHD 模塊進行數值模擬計算， 選用鎵銦錫合金作為磁流體發電介質[14]。 空載時選用誘導磁場法進行研究。 有負載時，考慮到磁流體發電通道的基本參數不變，只是負載電壓有所不同，不會引起誘導磁場的變化，因此選用電勢法進行研究。

2.1 邊界條件和初始條件設置

在仿真分析時需要設定磁流體發電通道的邊界條件和初始條件。 本文設定的兩個電極壁面為銅電極導電壁面； 邊界條件需滿足電流可以流過而液體不可以流過， 因此電極與液態金屬的接觸面采用耦合壁面。通道入口需要賦予一定的速度，因此設置速度入口，通道出口則設置為壓力出口，其余的壁面設置為絕緣壁面。在計算時，電極表面產生的電勢值的大小與負載系數的大小有關，正負極的電勢值。

2.2 發電通道數值模擬分析

本文的計算模型見圖1。 該模型為矩形發電通道，通道截面尺寸為0.04 m×0.24 m，通道長度為0.58 m。 如圖1 所示， 電極布設在發電通道中部，材質為銅，長度為0.26 m，寬度為0.04 m。磁場方向沿y 軸，分布區域為電流通過的區域，即與電極作用的區域一致。 發電通道其余壁面均設置為絕緣材質，且采用的液態金屬為鎵銦錫合金。通過對磁流體發電通道的三維模型進行數值模擬計算， 可研究不同負載系數和不同磁感應強度下發電通道內的流動現象。

當磁感應強度B 為0.5 T，負載系數k 分別為0.17，0.33，0.5，0.67 和0.83 時，發電通道內磁流體的速度變化規律如圖2 所示。從圖2 可以看出，在5 種負載系數下， 發電通道內磁流體的速度變化規律是相似的，即經過有效發電段時，邊界層速度急劇增大，負載系數越大，速度增大現象越明顯，且中心層的速度相對變低， 邊界層的速度則有增大的趨勢。

圖2 不同負載系數下的流場分布Fig.2 Flow field distribution under different load coefficients

當k 為0.83，B 分別為1.0 T 和0.5 T 時，近壁面y=0.119 與中心層y=0 的磁流體速度分布如圖3 所示（圖中，x 軸表示沿通道速度入口到出口的距離，0.0 m 處為速度入口，0.6 m 處為速度出口）。由圖3 可以看出，當B=1.0 T 時，邊界處的射流現象更加明顯， 增加磁場強度可以提高邊界處的最大射流速度。 對比近壁面與中心層的速度分布可以看出：在發電通道有效段入口處，中心層的速度迅速下降，近壁面的速度急劇增加；經過發電通道有效段時，由于受到洛倫磁力的影響，中心層的速度減小，近壁面的速度增大；靠近發電有效段出口處，中心層的速度繼續緩慢下降，近壁面的速度急劇增加。從圖3 還可以看出，近壁面處的磁流體在有效發電區間的入口速度和出口速度快速增加，并在有效發電區間x=0.4 m 附近達到最大值，而中心層的速度則相反。 由此表明， 在x=0.4 m 附近，速度剖面的波動程度比較大。通道內部的射流現象表明了液態金屬磁流體發電通道內部的誘導磁場會改變流場的分布。

圖3 不同磁感應強度下近壁面與中心層的速度分布Fig.3 Velocity distribution near wall and central layer under different magnetic field intensity

當磁流體發電機外接負載時， 依據數值模擬數據以及式（5），（6）可以得到如圖4 所示的電流和電壓隨負載系數的變化情況。從圖4 可以看出，隨著負載系數的增加，電壓也逐漸增加，而電流則逐漸減小，這一現象與理論分析相符合。這也充分表明，合理提高電壓可以有效提高發電性能，但負載系數的選定還需要結合其他條件進行綜合考慮。

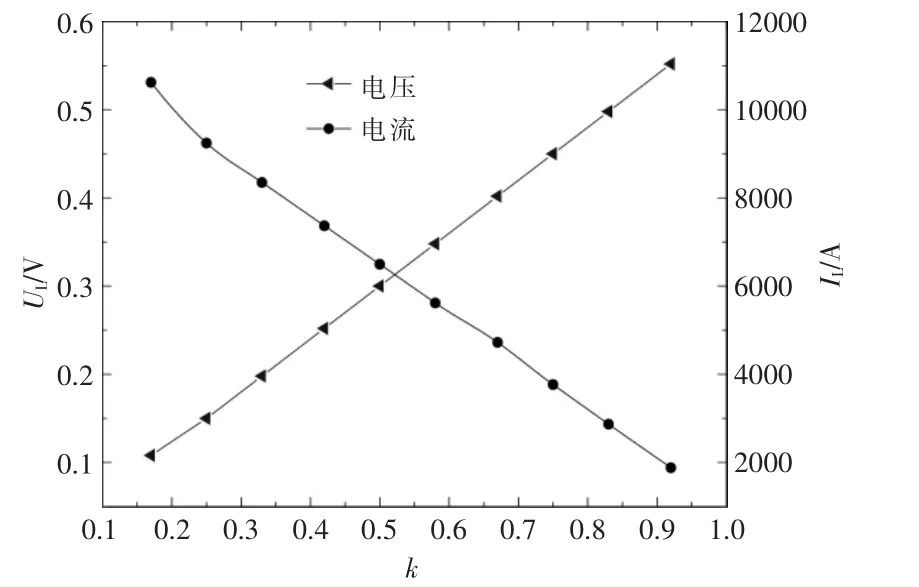
圖4 電流和電壓與負載系數的關系Fig.4 Relationship between current voltage and load factor

根據數值模擬數據和式（7）可以得到如圖5所示的發電通道輸出功率和負載系數的關系圖。從圖5 可以看出；當負載系數約為0.5 時，輸出功率取得最大值，最大值約為1.9 kW；當負載系數超過0.5 后，隨著負載系數的增加，輸出功率有逐漸減小的趨勢。

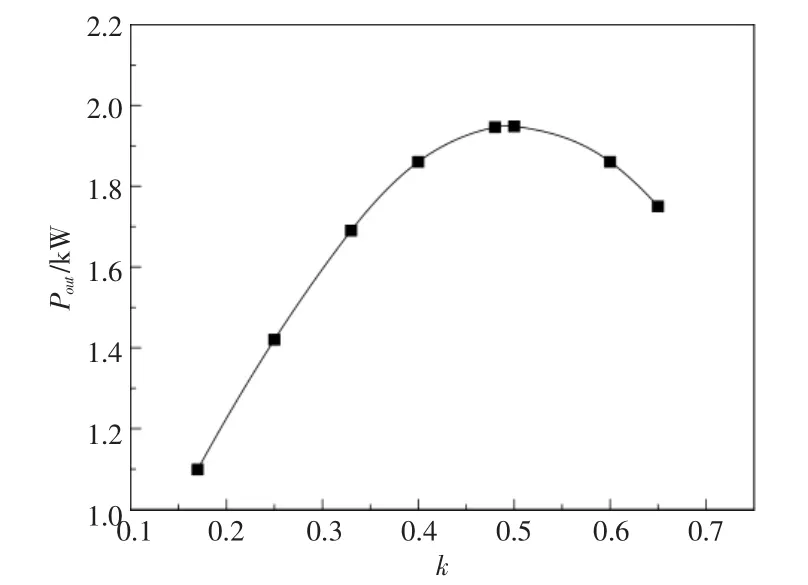
圖5 輸出功率與負載系數的關系Fig.5 Relationship between output power and load factor

根據數值模擬數據以及式（9），可以得到如圖6 所示的發電通道發電效率與負載系數的關系圖。 從圖6 可以看出，隨著負載系數的增加，發電效率先增大后減小， 并在k=0.67 附近取得最大值，最大值為29.2%。

圖6 發電效率與負載系數的關系Fig.6 Relationship between power generation efficiency and load factor

由圖5，6 可知，當負載系數k=0.5 時，輸出功率達到最大，而發電效率在k=0.67 附近取得最大值。 從圖2，3 可知，負載系數越大，發電通道內部磁流體速度的射流現象越明顯，越不利于發電機的發電性能。 因此，經過綜合考慮，筆者認為在負載系數k=0.6 附近， 液態金屬磁流體發電通道的發電性能可達到最好。

2.3 感應電動勢

設定通道寬度d 和入口速度為定值，外加磁感應強度為變量，以此來研究外加磁感應強度變化對發電通道感應電動勢U 的影響。 當d=0.24 m，ν=5 m/s 時， 外加磁感應強度與感應電動勢的關系如圖7 所示。從圖7 可以看出，感應電動勢隨著外加磁感應強度的增大而增大， 兩者呈現出正比例關系。 這一變化規律與理論計算的結果基本保持一致，但是，隨著外加磁感應強度的增加，實驗值與理論值的差值也越來越大。 這是因為隨著外加磁感應強度的增大， 由此產生的誘導磁場的強度也隨之增大， 而誘導磁場又會對電場產生干擾，造成感應電動勢的增幅減小。考慮到工程實際情況以及實驗室的實驗條件， 可取到的最大磁感應強度為0.8 T。

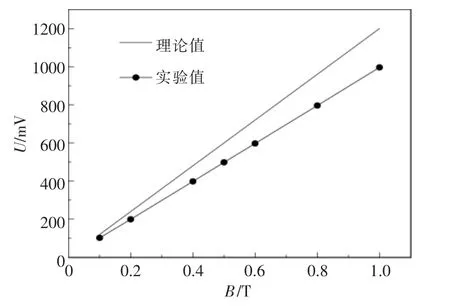
圖7 感應電動勢與外加磁感應強度的關系Fig.7 Relationship between induced electromotive force and applied magnetic field strength

設定通道寬度和外加磁感應強度為定值，入口速度為變量， 以此研究入口速度變化對感應電動勢的影響。當d=0.24 m，B=0.5 T 時，入口速度與發電通道感應電動勢的關系如圖8 所示。

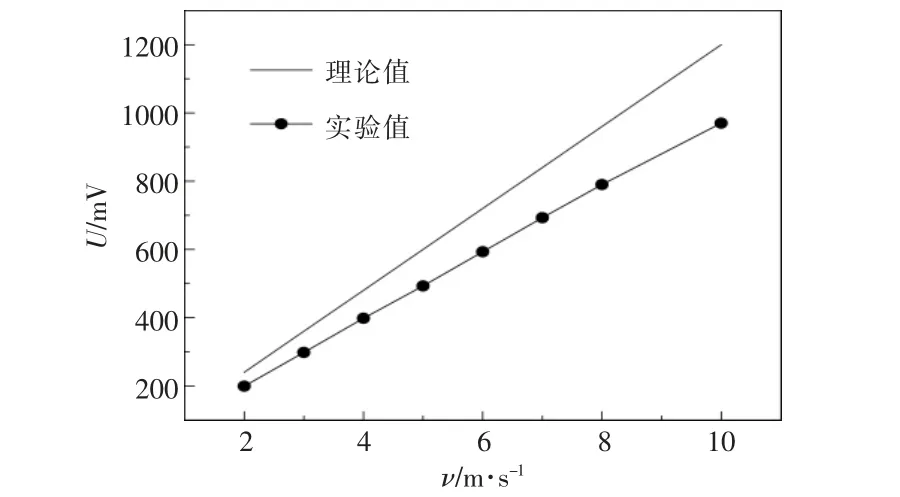
圖8 感應電動勢與入口速度的關系Fig.8 Relationship between induced electromotive force and inlet velocity

從圖8 可以看出：隨著入口速度的增大，感應電動勢近似呈線性增加；當ν＞7 m/s 時，感應電動勢增加的趨勢有減緩的傾向。 這表明當入口速度過大時，會造成感應電動勢的增加幅度減小。從圖8 還可以看出，隨著入口速度的增大，實驗值與理論值的差值也逐漸增大。在實際工程中，磁流體通過發電通道時的速度越快， 對產生感應電動勢越有利，但是，當磁流體的速度超過最適速度之后，這種有利的作用將會減弱。在實際工程中，入口速度越大，需要的成本以及所造成難度都會增大。因此，本文選取ν=7 m/s 作為優化后的入口速度。

當ν=5 m/s，B=0.5 T 時，發電通道感應電動勢隨通道寬度變化的規律如圖9 所示。 從圖9 可以看出：隨著通道寬度的增大，感應電動勢近似呈線性增加， 但是增加的幅度逐漸減緩， 當通道寬度d＞0.9 m 時，感應電動勢實驗值趨于穩定；通道寬度越大，實驗值與理論值的差值也越大。在實際工程中， 可通過不斷增大通道寬度來增加感應電動勢，但是，感應電動勢增加的趨勢會不斷減弱，同時通道寬度的增加會增加材料費用。因此，通道寬度的選取需要綜合考慮。 結合入口速度和外加磁感應強度， 本文選定d=0.9 m 作為優化后的通道寬度。

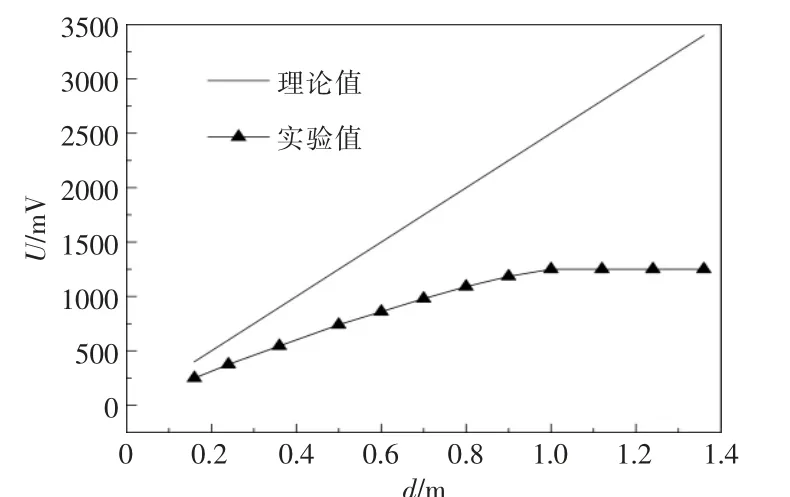
圖9 感應電動勢與通道寬度的關系Fig.9 Relationship between induced electromotive force and channel width

3 結論

①在不同負載系數下， 發電通道內磁流體速度變化的規律是相似的， 均存在經過有效發電段時，邊界層速度急劇增大的現象；負載系數越大，邊界層速度增大的現象越明顯， 且中心層的速度相對變低，邊界層的速度則有增高的趨勢。

②當外接負載時，隨著負載系數的增大，外電壓呈線性增長的趨勢，電流呈線性降低的趨勢；輸出功率和發電效率均隨著負載系數的增大呈現出先增大后減小的變化趨勢；發電效率在k=0.67 附近取得最大值，約為29.2%；輸出功率在k=0.5 附近取得最大值，約為1.9 kW。

③隨著入口速度、 磁感應強度和通道寬度的增大，感應電動勢均有增大的趨勢，但增大的趨勢會逐漸減小。 在已有設計的基礎上對發電通道參數進行優化，最后得到的最優參數為ν=7 m/s，B=0.8 T，d=0.9 m。