純電動汽車電驅動系統耦合動力學研究*

劉長釗，張 鐵，宋 健，尹顯頌，葛帥帥，2

（1.重慶大學，機械傳動國家重點實驗室，重慶 400044；2.重慶理工大學車輛工程學院，重慶 400054）

前言

近年來純電動汽車成為研究的熱點，而電驅動系統作為純電動汽車的心臟，取消了聯軸器和離合器，這不僅提高了系統的傳動效率，還降低了整車體積和質量。但是，電機轉子和齒輪系統直接耦合的方式容易造成齒輪嚙合狀態惡化，產生較大的振動和噪聲。同時，電驅動系統內存在多源復合激勵，如電磁轉矩、時變嚙合剛度、齒輪誤差和箱體柔性等，且電機電磁特性與齒輪內激勵特性存在交互作用，使得電驅動系統的動態特性更加復雜。因此，研究電驅動系統振動產生機理，特別是研究多源復合激勵對電驅動系統動態特性的影響，對提高系統集成設計能力和優化能力具有重要意義。

針對電動汽車齒輪系統，Setiawan等［1］通過建立變速器的數學模型，重點分析了變速器的瞬態動力學響應。Hou等［2］建立了考慮傳動系統柔性的動力學模型，分析了齒輪腹板和輪緣厚度對齒輪動態嚙合力矩的影響。Dabrowski等［3］建立了行星齒輪箱剛柔耦合模型，研究了傳遞誤差和齒輪制造誤差對箱體振動的影響。紀顯奇［4］建立了行星齒輪傳動系統模型，研究了齒輪傳遞誤差對傳動系統振動響應的影響。段元旺［5］利用有限元法研究了兩擋變速器的動力學特性。陶慶等［6］研究了行星齒輪傳動系統在不同齒圈厚度下的固有頻率。以上學者主要研究齒輪傳動系統的固有特性和動態特性，但對機電耦合的研究不足。

針對電機模型，邱家俊等［7］研究了電機啟動時轉子軸在交變電磁力矩作用下的振動特性。Park等［8］利用傳遞矩陣法建立了電機轉子系統動力學模型，研究結果表明機電耦合系統的振動響應幅值比純機械系統的響應幅值大。Mandic等［9］通過主動控制減小了電機轉子系統的扭轉振動。Xiang等［10］研究了在不平衡磁拉力作用下永磁同步電機轉子的穩定性和頻響特性。陳星［11］建立了車用永磁同步電機轉子軸系動力學模型，研究了電磁參數和結構參數對轉子振動的影響規律。左曙光等［12］建立了考慮定子各向異性的永磁同步電機模型，通過優化定子軛的厚度來降低電機振動的峰值。以上研究建立了電機轉子振動機電耦合模型，但對于一體化電驅動系統，電機電磁轉矩通過轉子傳遞到齒輪傳動系統，電機和齒輪系統的耦合作用比單轉子的耦合問題更加復雜，因此需要建立一個計入齒輪傳動系統的機電耦合動力學模型。

針對電動汽車電驅動系統機電耦合特性，于蓬等［13］建立了考慮結構柔性的電動汽車傳動系統機電耦合動力學模型，研究了控制策略對多物理場耦合作用下系統動態特性的影響。Hu等［14］建立了電機和傳動系統耦合的瞬態動力學模型，利用一種主動阻尼控制策略抑制了傳動系的扭轉振動。Fan等［15］建立了雙電機耦合驅動系統（DCDS）的動力學模型，研究了齒輪嚙合剛度和電磁激勵對系統動態特性的影響。Yi等［16］建立了包含電機的多級齒輪傳動系統動力學模型，研究了電磁扭轉剛度對系統固有特性的影響。葛帥帥等［17］建立了電動汽車電驅動系統機電耦合動力學模型，分析了典型工況下齒輪系統扭轉特性和定子電流的動態響應特性，結果表明電機和齒輪系統之間存在強耦合效應。Chen等［18］建立了開關磁阻—行星齒輪電驅動系統模型，研究了萬向節對系統特性的影響，結果表明引入萬向節會增強電機與行星輪系統之間的耦合效應。以上學者的機電耦合動力學特性的研究考慮了齒輪傳動系統和電機系統的內激勵，但齒輪系統與電機系統的動力學模型進行了相應簡化，忽略了軸段、殼體柔性以及電機電磁徑向力的影響。

純電動汽車電驅動系統是高度集成的機電系統，因此本文提出了一種適用于變速等非穩態工況且綜合考慮電磁激勵、齒輪內激勵以及一體化系統結構特性的機電耦合動力學模型，研究了穩態和加速工況下多源激勵對電驅動系統動態特性的影響。

1 電驅動系統耦合動力學建模

圖1為純電動汽車電驅動系統結構簡圖，主要分為永磁同步電機、齒輪傳動系統和箱體3部分。

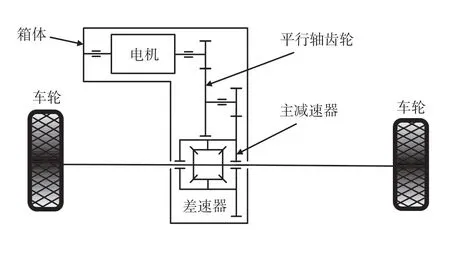
圖1 純電動汽車電驅動系統結構

1.1 永磁同步電機動力學建模

本文采用有限元法建立永磁同步電機模型，首先利用有限元軟件導出電機的徑向和切向磁通密度，然后根據Maxwell應力張量理論，得到徑向和切向電磁力密度p（rθ，t）、p（tθ，t）：

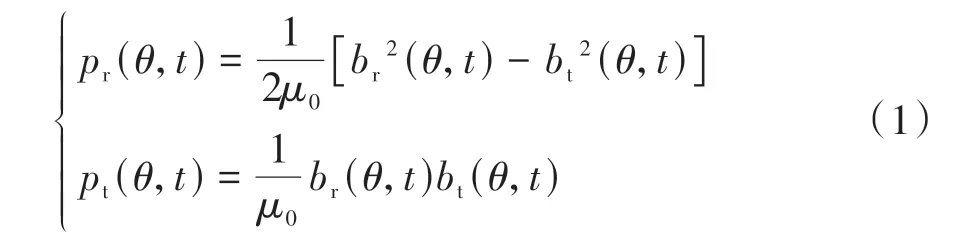
式中：μ0為空氣磁導率，為4π×10-7H/m；br、bt分別為徑向和切向氣隙磁密。圖2為電機的徑向和切向電磁力密度時空分布圖，將得到的電磁力密度在定子齒所在的區間上積分，即可得定子齒所受的集中電磁力。

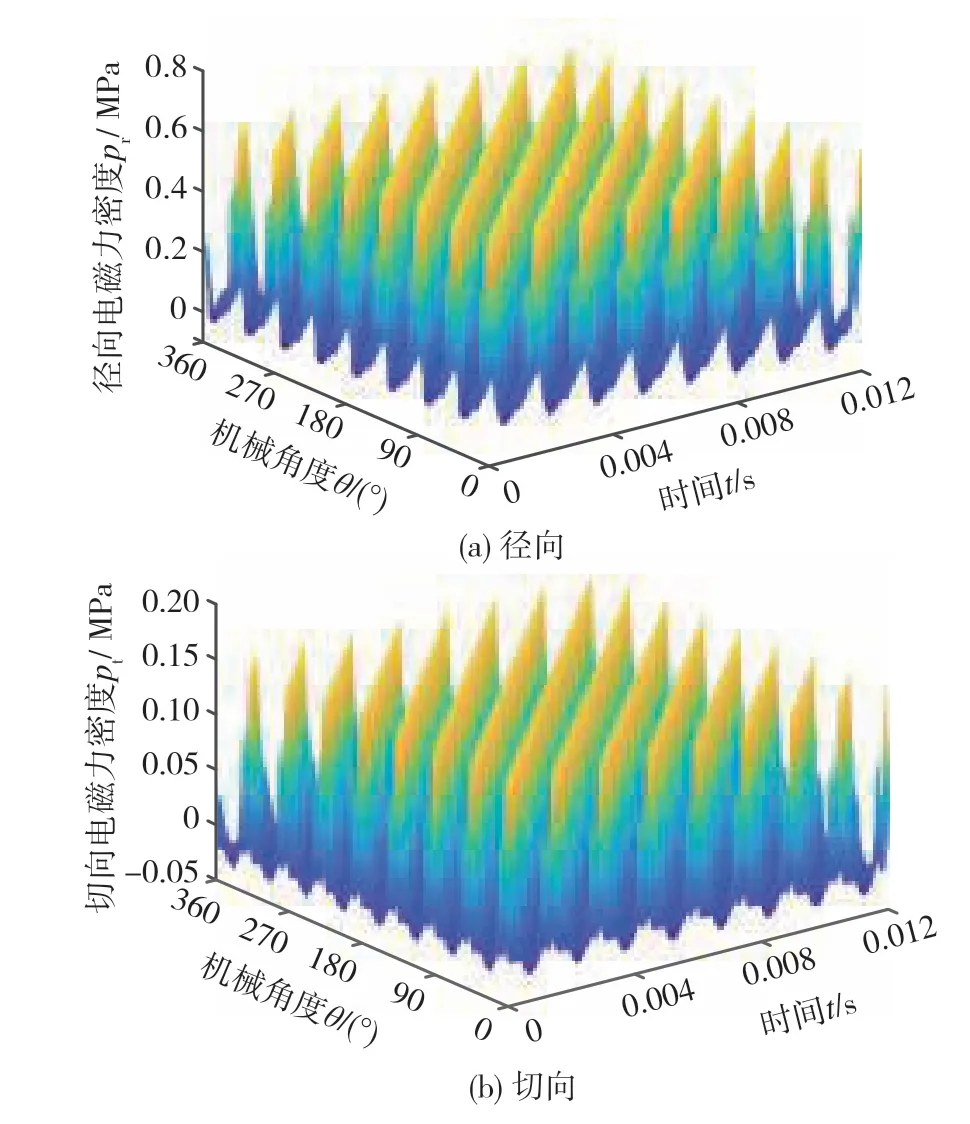
圖2 電機電磁力密度

圖3為第n個定子齒的受力分析圖，為便于與箱體耦合，將集中電磁力轉換到直角坐標系中，坐標變換矩陣如式（2）所示。其中：Frn、Ftn分別為第n個定子齒所受徑向和切向電磁力；Fxn、Fyn、Fzn分別為直角坐標系下x、y、z方向上的力。

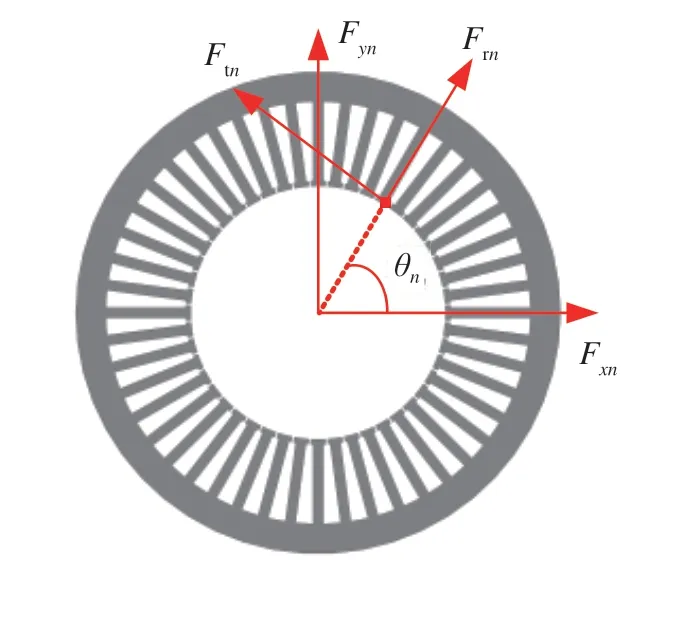
圖3 電機定子齒受力分析

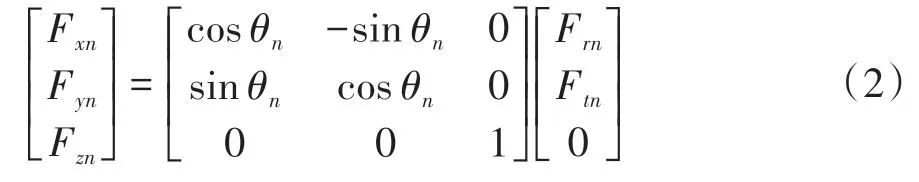
1.2 旋轉構件和箱體有限元縮聚模型

1.2.1 模態縮聚理論

系統的運動方程由式（3）表示，其中：M、Cd、K分別為系統質量、阻尼、剛度矩陣；u為位移矢量；F為載荷矢量。

式（3）可在模態坐標下解耦，如式（4）所示。其中：yj為系統第j階模態坐標；ξj、ωj分別為第j階模態阻尼比和模態頻率；Φj為第j階振型矢量；ndof為總自由度數。

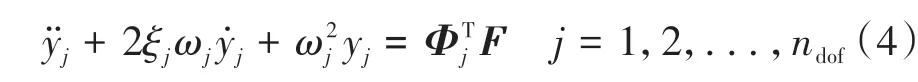
高階模態的影響一般是有限的，為簡化計算，可求解式（4）的前n個方程，則得到狀態方程：

其中：

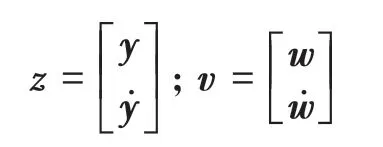
式中：y是模態坐標向量；w是系統的集中節點位移列陣分別是狀態空間矩陣。

1.2.2 有限元縮聚模型

圖4為電機轉子軸集中節點劃分示意圖。其中：轉子縮聚節點用于輸入電磁轉矩；軸頸縮聚節點1、2用于耦合軸承單元；齒輪縮聚節點用于建立嚙合單元。

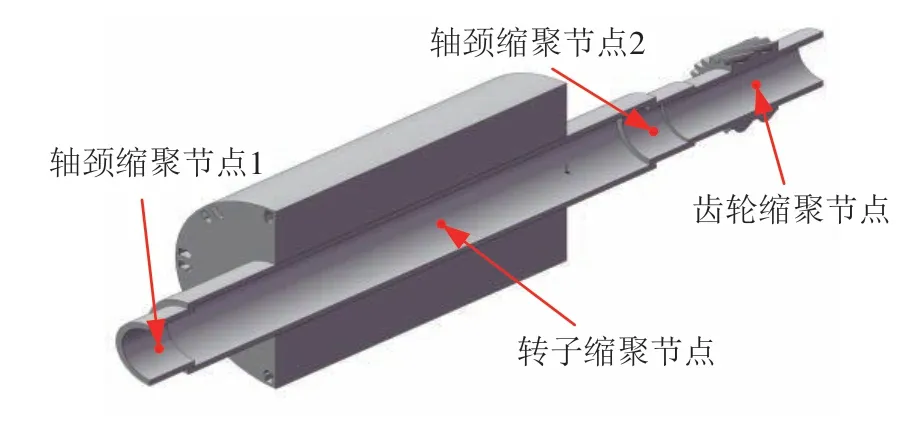
圖4 電機轉子軸縮聚模型主節點劃分

中間軸和差速器殼體集中節點劃分如圖5所示，集中節點分別為軸頸和各齒輪的理論中心。

箱體主要集中節點劃分如圖6所示，箱體通過集中節點和系統其它部件進行耦合。

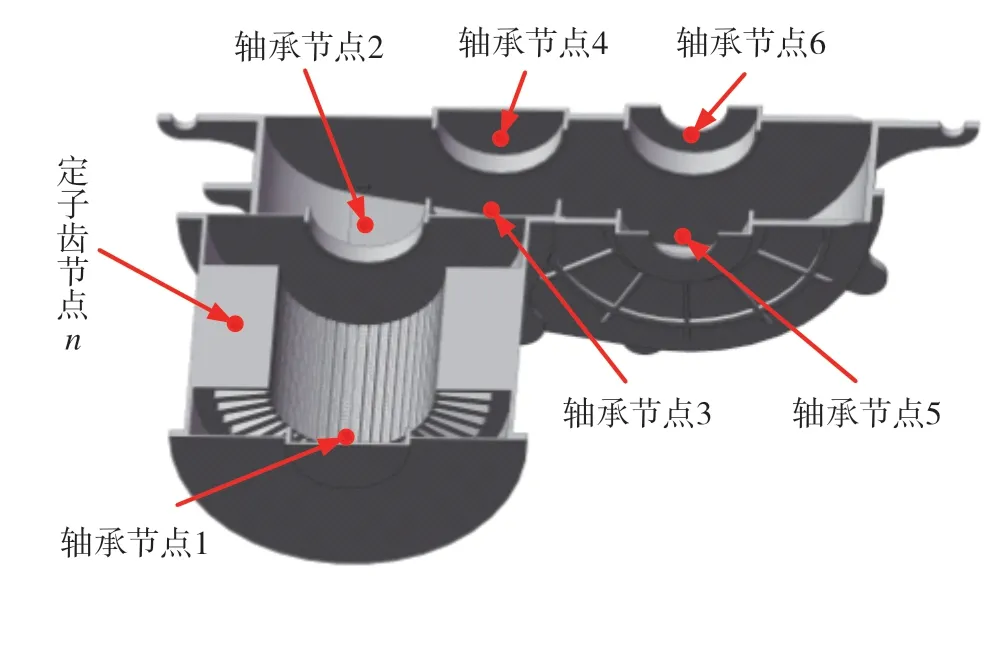
圖6 箱體縮聚模型主節點劃分

1.3 平行軸斜齒輪動力學建模

圖7為主動輪右旋且繞z軸逆時針旋轉的斜齒輪副6自由度動力學模型。齒輪副沿嚙合線方向的總變形δ為

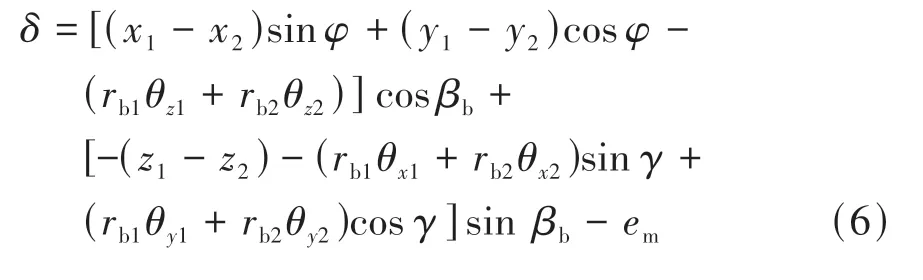
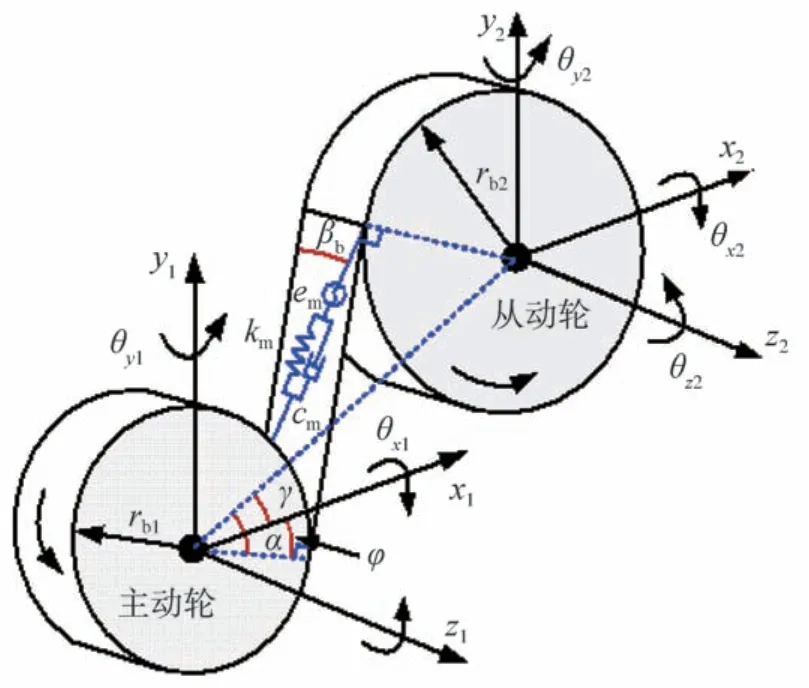
圖7 斜齒輪嚙合模型

式中：xi、yi、zi分別為齒輪（ii=1、2）在x、y、z方向上的平移位移；θxi、θyi、θzi分別為齒輪（ii=1、2）在x、y、z方向上的角位移；φ為主動輪上垂直于嚙合面的半徑與x正方向的夾角；rb1、rb2分別為主、從動輪的基圓半徑；γ為嚙合線與x軸正向的夾角；βb為基圓螺旋角；em為齒輪誤差；km為嚙合剛度。

本文將齒輪副的時變嚙合剛度表達為齒輪角位移的函數，并使之用于變速過程。同時考慮齒輪加工過程中的誤差，用偽隨機數來模擬齒輪誤差激勵，圖8和圖9分別為一級齒輪副的時變嚙合剛度和齒輪誤差激勵。

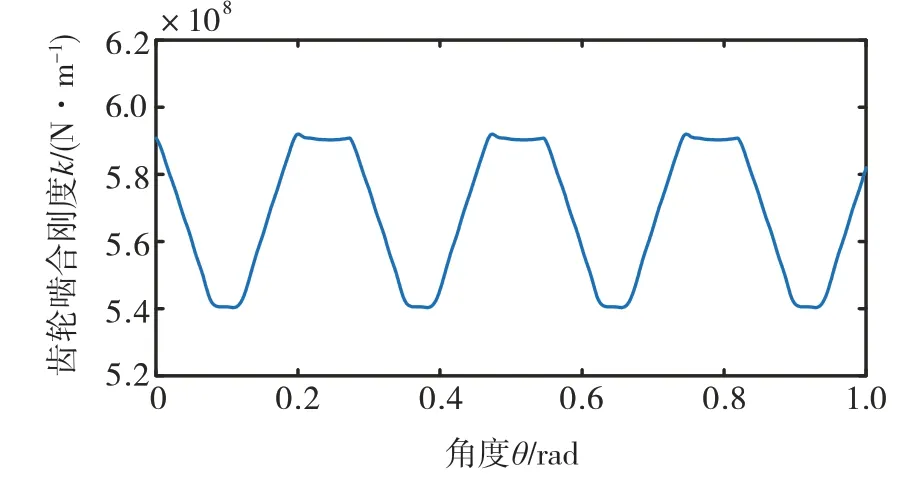
圖8 一級齒輪副時變嚙合剛度

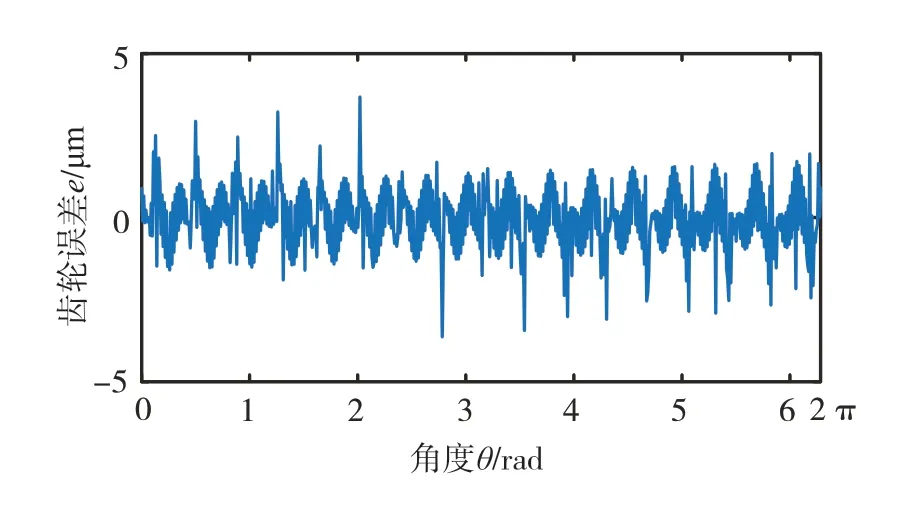
圖9 一級齒輪副齒輪誤差

考慮齒側間隙后齒輪副沿嚙合線方向的總變形如式（7）所示。

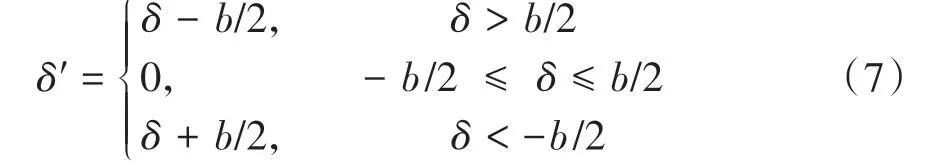
式中：δ、δ′分別為考慮齒側間隙前后齒輪副沿嚙合線方向的總變形；b為齒側間隙。

1.4 差速器動力學建模

直齒錐齒輪副的嚙合模型如圖10所示。其中：rbj是直齒錐齒輪j的嚙合點半徑；δb為錐齒輪節錐角；αn為法面壓力角；k、c、e分別為嚙合剛度、嚙合阻尼、綜合齒輪誤差。

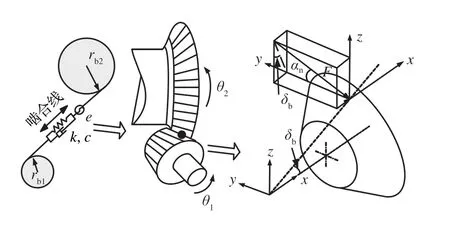
圖10 直齒錐齒輪嚙合模型及受力分析

則直齒錐齒輪副沿嚙合線的相對總變形為

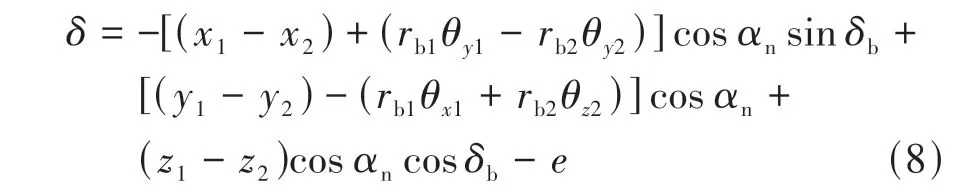
差速器動力學模型如圖11所示。圖中建立了3個坐標系：（1）靜止坐標系OXYZ；（2）隨差速器殼體轉動的動坐標系oxyz；（3）原點位于行星齒輪中心的動坐標系opnxpnypnzp（nn=1，2，…，N，N是行星齒輪個數）。其中：符號x、y、z、θ分別為x、y、z方向上的平移位移和角位移；下標p、b、c分別代表行星齒輪、半軸齒輪、差速器殼體，以上構件各方向上的位移都是在動坐標oxyz中測量的；θc為差速器殼體在靜止坐標系OXYZ中測得的轉角；φn是第n個行星齒輪的位置角，φn=2π（n-1）/N；Tm為作用在第m個半軸齒輪上的阻力矩。

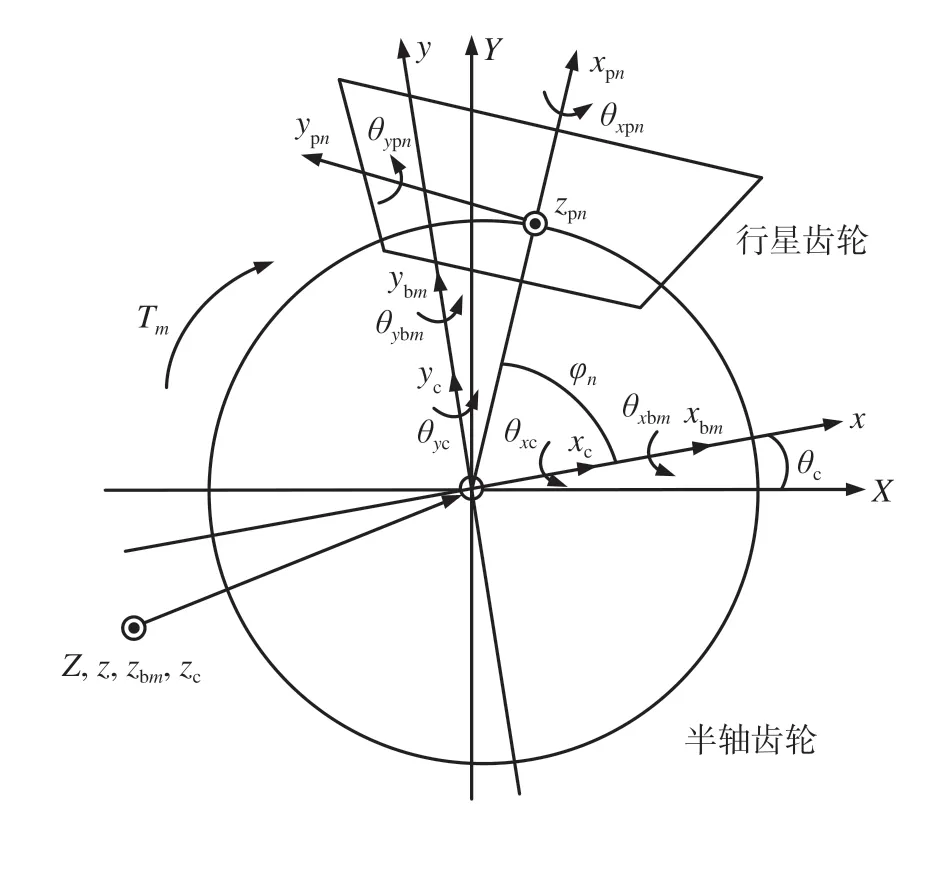
圖11 差速器動力學模型

利用非慣性坐標系的牛頓定律來獲得第m個（m=1，2）半軸齒輪的運動微分方程，如式（9）所示。其中：mb、Jxb、Jyb和Jzb分別是半軸齒輪的質量和繞自身x、y、z軸的轉動慣量；FPB（x，y，z）bnm和MPB（x，y，z）bnm分別為行星齒輪作用在半軸齒輪上的力和力矩；下標n（n=1，2）、m（m=1，2）分別代表第n個行星齒輪和第m個半軸齒輪；kxb、kyb、kzb、ktxb和ktyb分別為半軸齒輪在x、y、z、θxb、θyb向的接觸剛度；cxb、cyb、czb、ctxb和ctyb分別為半軸齒輪在x、y、z、θxb、θyb向的接觸阻尼；δbmcx、δbmcy、δbmcz、θδbmcx和θδbmcy分別表示第m個半軸齒輪與差速器殼體在各個方向的相對位移。

第n個行星齒輪的運動微分方程如式（10）所示，式中各符號含義與式（9）中類似。

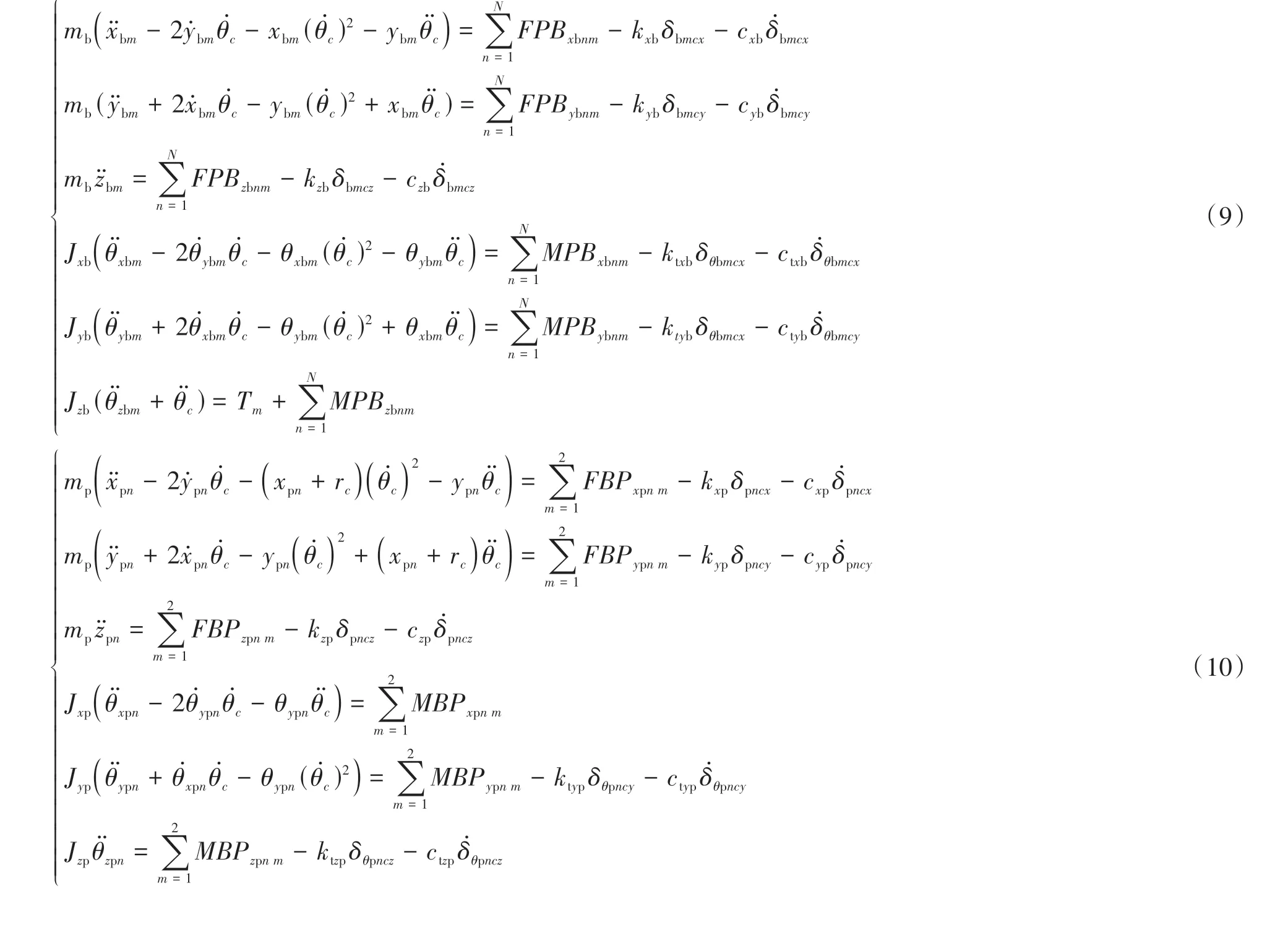
1.5 電驅動系統機電耦合模型

電驅動系統主要參數如表1所示。根據永磁同步電機模型和傳動系統動力學模型，建立電驅動系統機電耦合模型，如圖12所示。

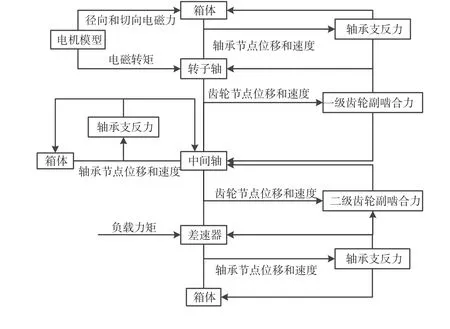
圖12 耦合系統動力學建模流程圖

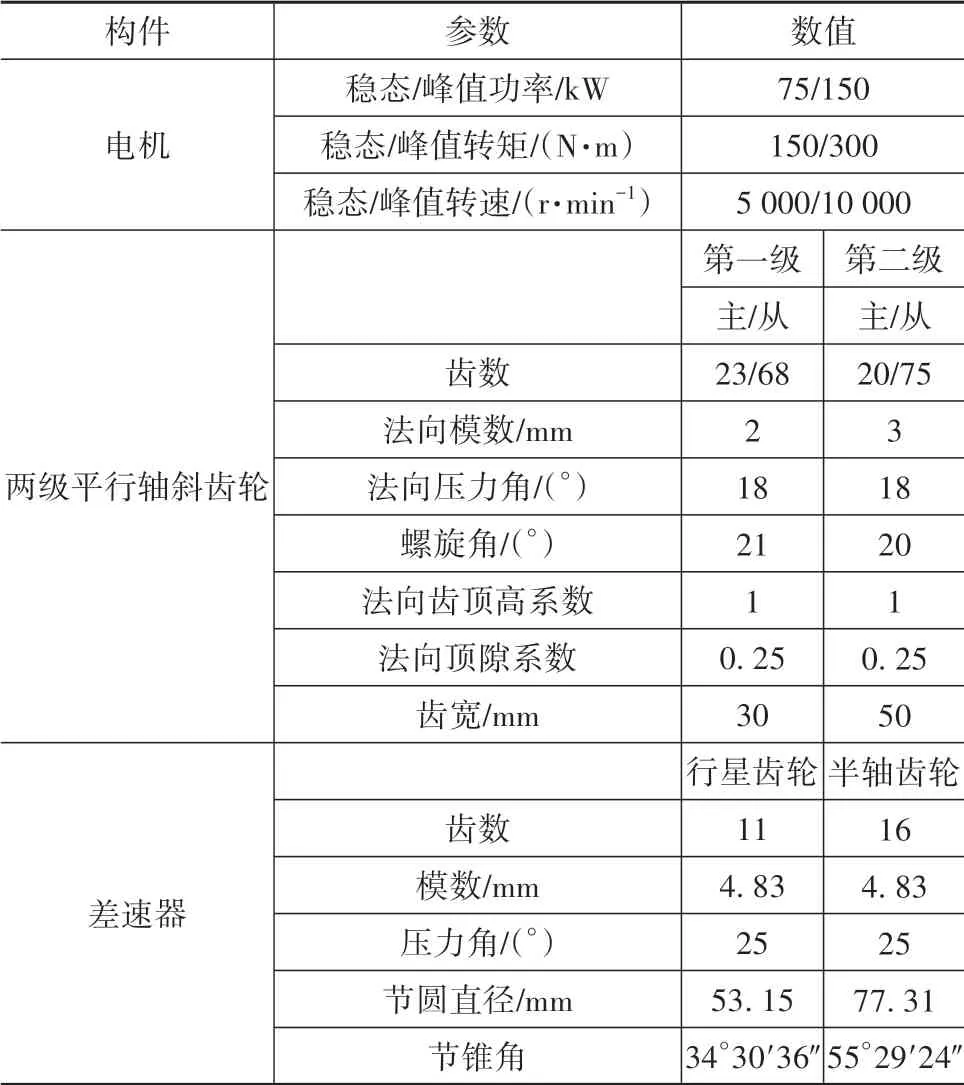
表1 電驅動系統主要參數

系統各構件之間以相互作用力和位移關系進行耦合。電機的電磁轉矩作為驅動力矩作用在轉子軸上，徑向和切向電磁力作用在與箱體耦合的定子齒上，負載力矩作用在差速器上；根據齒輪節點的位移和速度計算齒輪副嚙合力，且通過轉子軸和中間軸上的齒輪傳遞嚙合力；利用旋轉構件和箱體在軸承節點上的相對位移和相對速度來計算軸承的支反力，然后所有軸系通過軸承支反力與箱體耦合。

2 穩態工況下系統動態特性研究

2.1 有限元驗證縮聚模型正確性

為了從動力學角度驗證箱體縮聚模型的正確性，在縮聚模型和有限元軟件中分別對箱體軸承集中節點2（位置見圖6）在X、Y、Z方向施加5 000 N的集中力。有限元軟件中計算得到集中節點2的變形位移其值為687.96 μm。縮聚模型中集中節點2的動態位移如圖13所示，兩者結果的相對誤差為4.38%，說明縮聚模型與有限元模型的計算結果吻合較好。

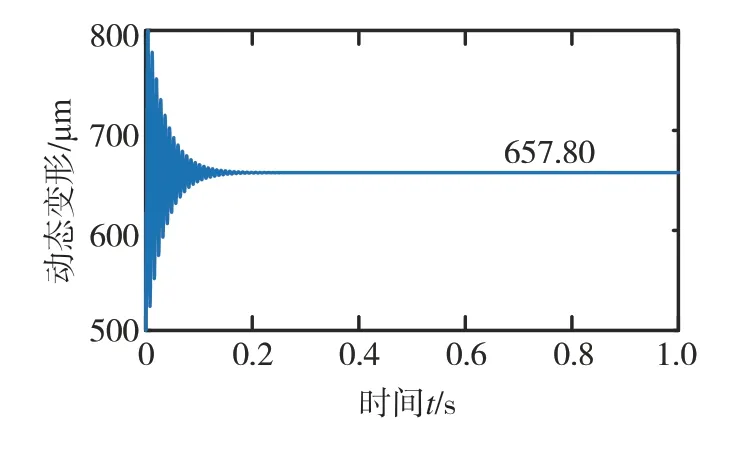
圖13 軸承集中節點2動態位移

在有限元軟件中設轉子軸轉速為1 000 rad/s，提取轉子軸外表面網格節點（節點序號為35818）在徑向的變形位移，其值為2.51 μm，圖14為該轉子網格節點位置示意圖。在縮聚模型中以相同轉速對轉子軸進行動力學仿真，該網格節點在徑向的動態位移如圖15所示。該節點動態位移收斂到2.48 μm，與有限元模型的絕對誤差為0.03 μm，相對誤差為1.2%，結果吻合較好，驗證了所建模型的正確性。

圖14 轉子網格節點選取

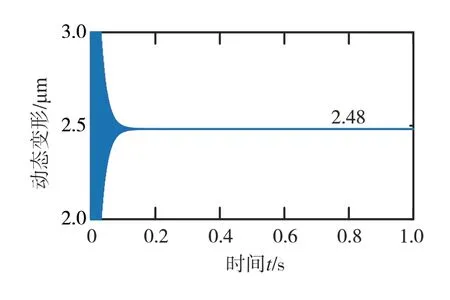
圖15 網格節點徑向動態位移

2.2 內部激勵對系統動態特性的影響

2.2.1 電機轉矩波動的影響

（1）齒輪動態嚙合力矩

圖16為電機輸出轉矩頻譜圖。電機轉矩的頻率成分主要是電機基頻fmb=2000 Hz及其倍頻。

圖16 電機轉矩頻譜

圖17為電機轉矩波動對一級齒輪副動態嚙合力矩影響的時域圖及頻譜圖。由圖可知，恒定電機轉矩時齒輪副動態嚙合力矩波動范圍較小，在考慮電機轉矩波動后，齒輪副動態嚙合力矩均值不變，但波動的幅值明顯增大；頻譜圖上出現了電機轉矩的頻率，主要成分為fmb和2fmb，且2fmb對應的幅值大于齒輪副嚙合頻率的幅值，這表明電機轉矩波動通過轉子軸傳遞到了齒輪系統上，并且對齒輪動態嚙合力矩的影響較大。

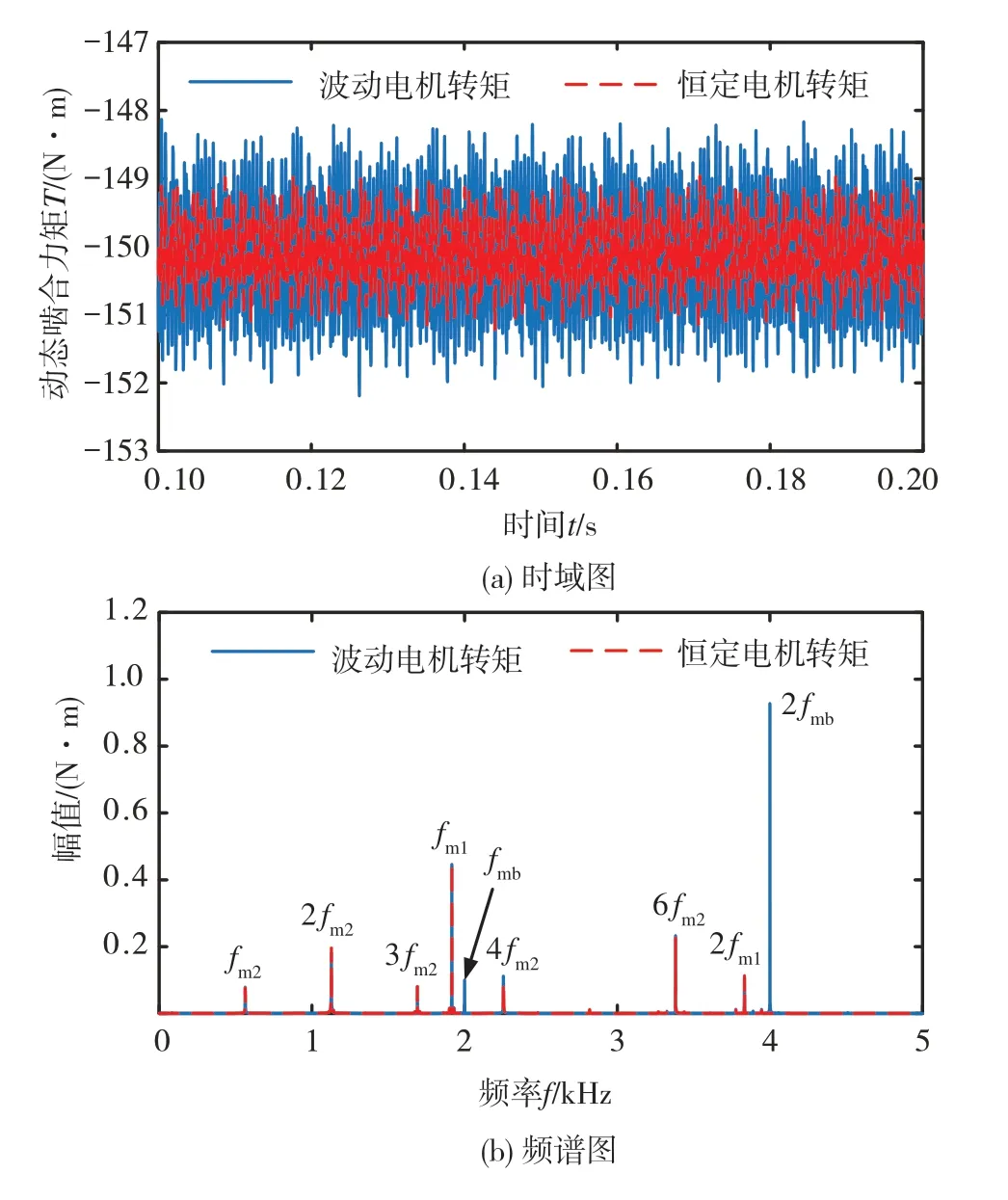
圖17 一級齒輪副動態嚙合力矩時域及頻譜圖

圖18為二級齒輪副動態嚙合力矩時域圖及頻譜圖。由圖18（a）可知：電機轉矩波動對二級齒輪副動態嚙合力矩有影響，但影響較小；頻譜圖上，二級齒輪副中電機轉矩頻率與嚙合頻率幅值的差值顯著減小，但仍然出現了電機電磁頻率成分2fmb。這是因為在嚙合阻尼和結構阻尼的作用下，同時受到傳遞路徑的影響，距離電機較近的構件受到電磁轉矩波動的影響明顯，較遠的構件所受到的影響較小。

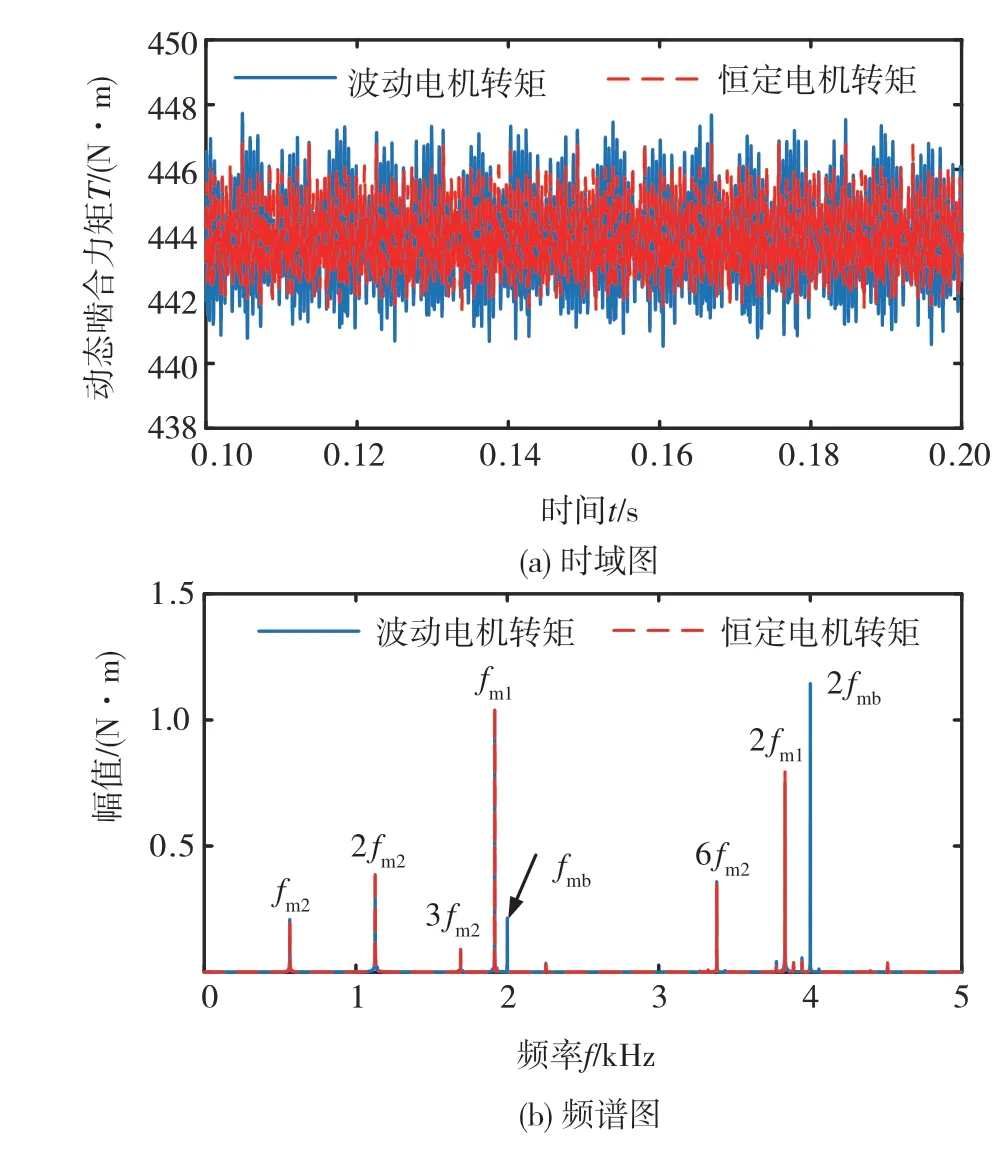
圖18 二級齒輪副動態嚙合力矩時域及頻譜圖

（2）軸承動態支反力

圖19為電機轉矩波動對軸承2（位置為圖6中軸承節點2）動態支反力影響的時域圖及頻譜圖。由此可知，兩條曲線基本重合，主要頻率成分為電機轉頻fr1和齒輪嚙合頻率fm1，而電機轉矩頻率fmb幅值很小，即電機轉矩波動對軸承動態支反力的影響很小。

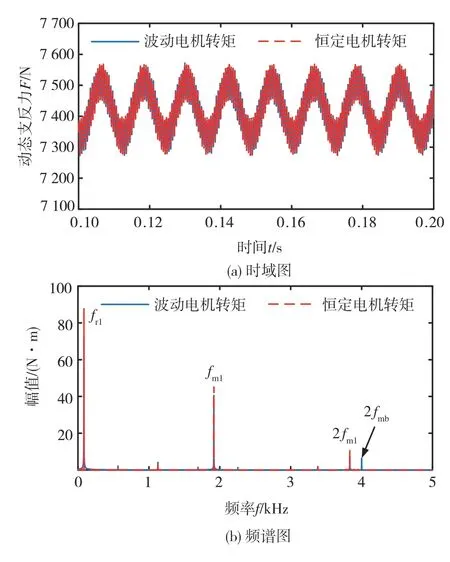
圖19 軸承2動態支反力時域及頻譜圖

2.2.2 齒輪誤差的影響

（1）齒輪動態嚙合力矩

圖20為齒輪誤差對一級齒輪副動態嚙合力矩影響的時域圖。由此可知，齒輪動態嚙合力矩在考慮齒輪誤差后波動幅值顯著增加，遠大于電機轉矩波動對動態嚙合力矩的影響。

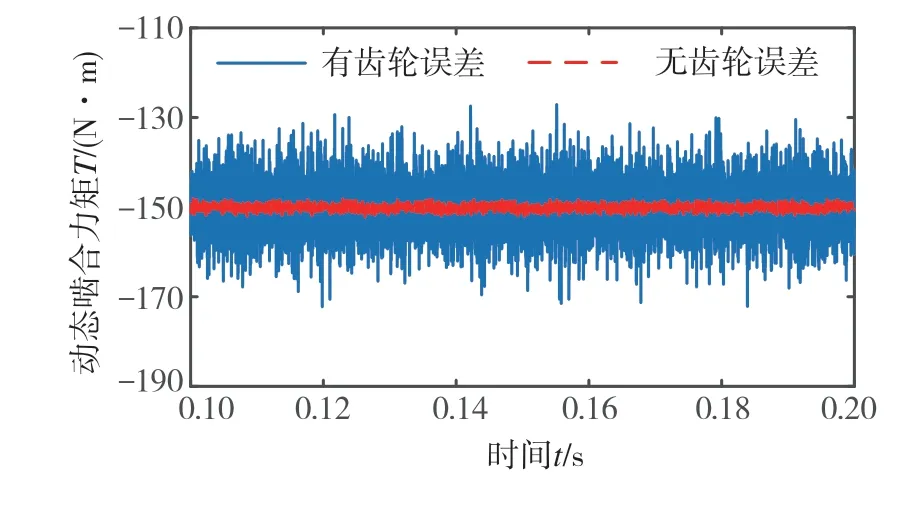
圖20 一級齒輪副動態嚙合力矩

圖21為一級齒輪副齒輪誤差頻譜圖，圖22為一級齒輪副動態嚙合力矩頻譜圖。由圖21可知，頻譜圖上出現了連續的區域，這是因為本文以偽隨機數模擬齒輪誤差，頻率成分復雜。結合圖21和圖22，可以發現在高頻區域中的頻率成分主要來自于齒輪誤差。這說明一級齒輪副動態嚙合力矩的幅值增大，齒輪誤差激勵起到了關鍵性的影響。

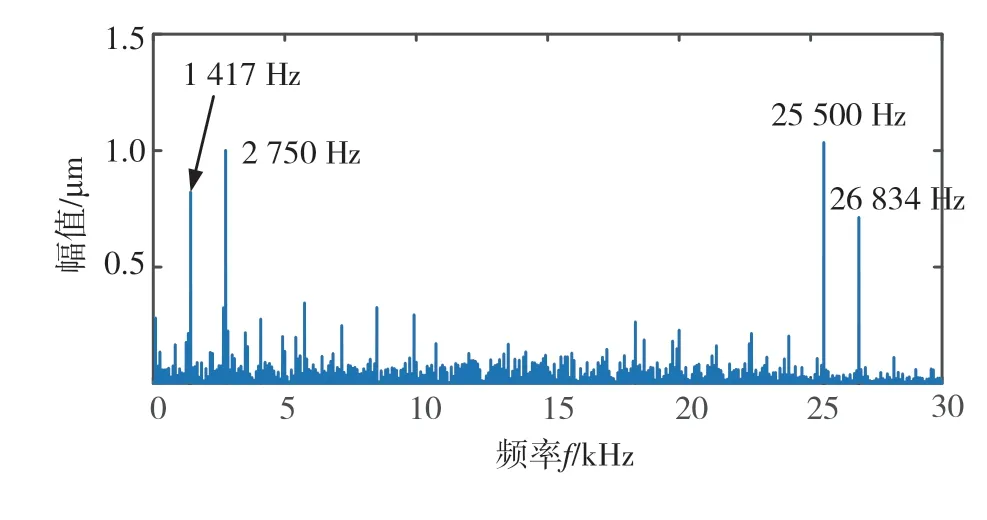
圖21 一級齒輪副齒輪誤差頻譜圖

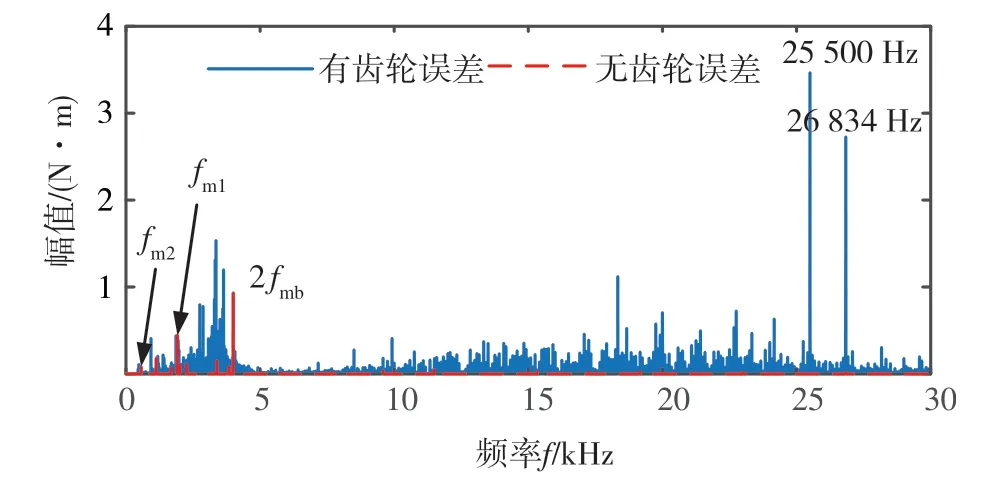
圖22 一級齒輪副動態嚙合力矩頻譜圖

（2）軸承動態支反力

圖23和圖24分別為齒輪誤差對軸承1、2（位置見圖6）動態支反力影響的時域圖及頻譜圖。從圖23中可以看出：考慮齒輪誤差后軸承動態支反力波動明顯增加；頻譜出現了幅值較大的成分1 417 Hz，該頻率可以在圖21中找到，這表明了齒輪誤差激勵作用在齒輪副上，然后通過傳動軸傳遞到了軸承上。

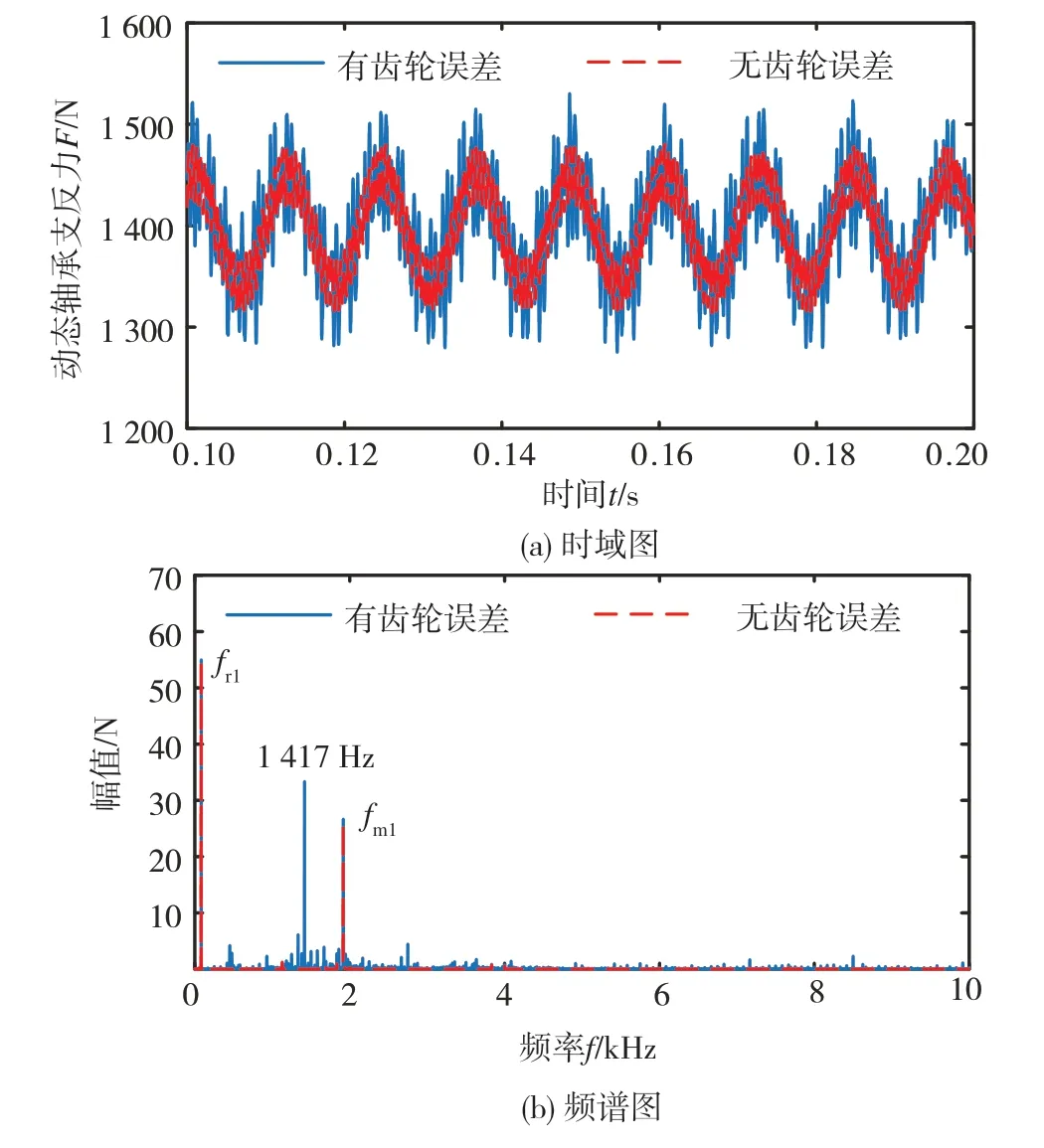
圖23 軸承1動態支反力時域及其頻譜圖

對比圖23和圖24，發現軸承2的動態支反力頻譜范圍更寬，頻率成分更復雜，這是因為軸承2的安裝位置離齒輪副更近，由齒輪嚙合產生的激勵力傳遞到軸承2處，對軸承2的影響更加明顯。由圖24可知，軸承2的動態支反力頻率范圍主要集中在0～15 000 Hz，引入齒輪誤差后產生的高頻成分如25 500 Hz和26 834 Hz的幅值較小，這表明高頻成分對軸承支反力的影響不大。

圖24 軸承2動態支反力時域及其頻譜圖

2.2.3 箱體對系統動態特性的影響

（1）齒輪動態嚙合力矩

圖25為耦合箱體前后一級齒輪副動態嚙合力矩時域圖和頻譜圖。可以看出耦合箱體前后齒輪副動態嚙合力矩的均值和振幅基本不變，且頻率成分變化也較小，說明耦合箱體對齒輪動態嚙合力矩的影響不大。這是因為齒輪副動態嚙合力矩主要受外載荷、齒輪嚙合剛度和齒輪誤差等因素的影響，而耦合箱體前后外載荷、嚙合剛度和齒輪誤差基本不變，故耦合箱體后齒輪動態嚙合力矩的變化不大。

圖25 一級齒輪副動態嚙合力矩時域及頻譜圖

（2）軸承動態支反力

圖26為耦合箱體前后軸承1、2的動態支反力時域圖。可以看出耦合箱體后軸承1的動態支反力均值變小，而軸承2的動態支反力均值則略微增大，這是因為在不同軸承位置處薄壁箱體的壁厚及結構設計不同，導致等效支撐剛度也不同。因此耦合箱體后集中節點處的動態位移將發生變化，導致軸承力隨之而改變。耦合箱體后，軸承1的等效支撐剛度變化更大，故其動態支反力變化也更大。

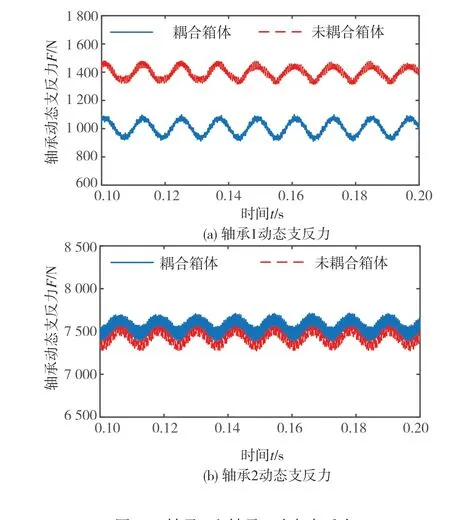
圖26 軸承1和軸承2動態支反力

3 加速工況下系統動態特性研究

當路面擁堵時，汽車頻繁起停和加速，導致驅動電機長時間運行在變速工況下。在電驅動系統調速過程中，當內外部激勵頻率跨越系統固有頻率時，系統可能發生共振，這會影響到汽車行駛過程的可靠性和安全性。因此本節分析了加速過程下系統的共振情況。本節將一體化電驅動系統分為耦合系統（耦合箱體）和齒輪傳動系統（不耦合箱體），并對兩者展開研究。

3.1 加速工況下齒輪傳動系統共振分析

3.1.1 齒輪傳動系統特征值計算

特征值反映了系統的穩定性，因此在進行共振分析之前，需要先計算系統的特征值。特征值的實部表示系統衰減系數，虛部對應固有頻率。對于具有一般阻尼的系統，其特征值可能為實數，也可能是具有負實部的復數，復特征值將成對存在，且會出現虛部為0的特征值，因此表2只給出虛部絕對值大于零的部分階數特征值。

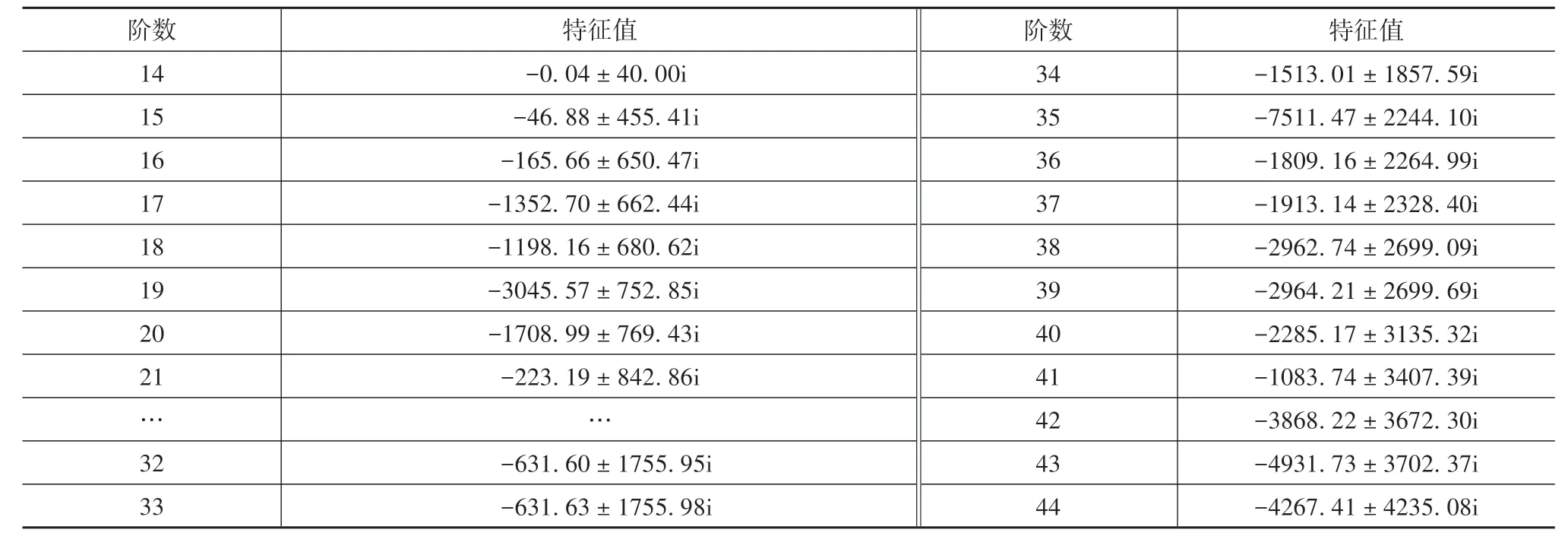
表2 不耦合箱體下系統特征值

分析可得：（1）特征值實部全為負實數，表明系統趨于穩定；（2）在某些相鄰的階數，如32階和33階、38階和39階等特征值十分接近，這是因為系統中軸承支撐剛度在水平和豎直方向的數值相同，均等于徑向支撐剛度。

3.1.2 齒輪傳動系統共振分析

為分析系統的共振，讓驅動電機的轉速從0勻速上升到10 000 r/min，圖27為加速過程中電機轉速及轉矩激勵時域圖。為使圖片清晰，轉矩激勵時域圖只給出了仿真前0.2 s的數據。

圖27 電機轉速及轉矩激勵

（1）不考慮齒輪誤差

圖28為系統在不考慮齒輪誤差時一級齒輪副動態嚙合力矩時域圖，為了消除仿真初始的瞬態波動，仿真前0.3 s的數據未采用。可以看出，在0.44、0.88、1.70和3.70 s附近，動態嚙合力矩的振幅明顯增大，表明這幾個時刻所對應的電機轉速為系統的共振轉速。

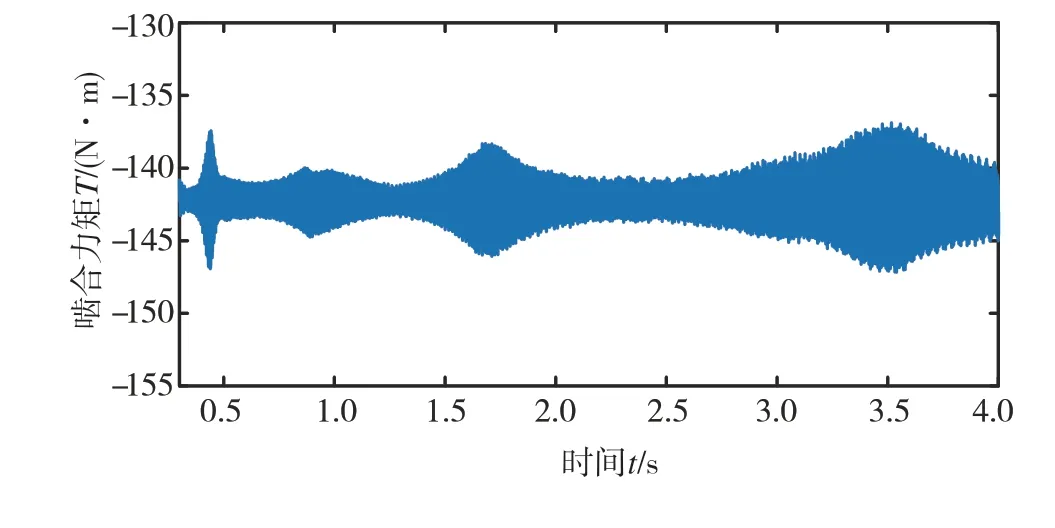
圖28 一級齒輪副動態嚙合力矩時域圖

采用短時傅里葉變換（STFT）獲得如圖29所示的動態嚙合力矩時頻圖，與橫坐標平行的直線代表系統固有頻率，紅色斜線代表激勵頻率。

圖29 一級齒輪副動態嚙合力矩時頻圖

可以看到，導致系統共振的主要激勵頻率成分為電機轉矩頻率fmb、齒輪副嚙合頻率fm1和fm2。

（2）考慮齒輪誤差

圖30為加速過程中考慮齒輪誤差時一級齒輪副動態嚙合力矩時域圖。可以看出，考慮齒輪誤差后齒輪副動態嚙合力矩均值不變，但是波動幅值明顯增大，這與穩態工況下的結論類似。同時，共振峰難以從時域圖上識別，必須從頻域分析。

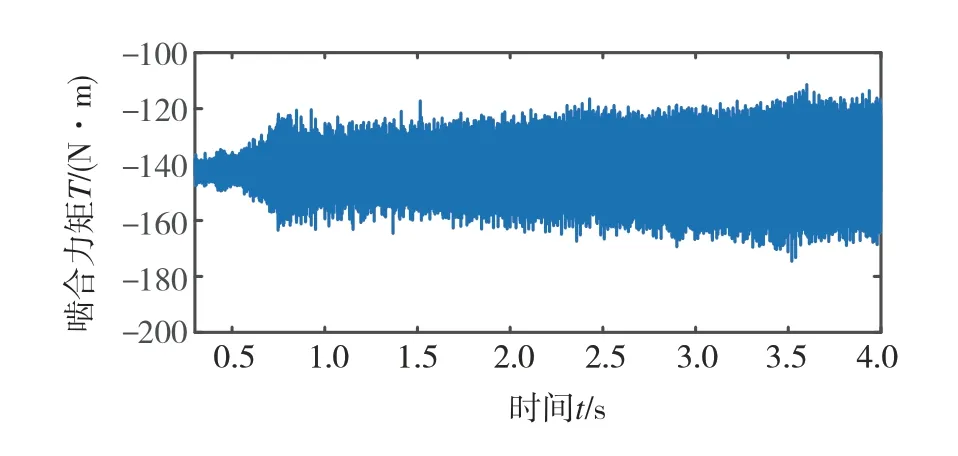
圖30 一級齒輪副動態嚙合力矩時域圖

圖31為加速過程中考慮齒輪誤差時一級齒輪副動態嚙合力矩時頻圖。可以看出導致系統發生共振的激勵頻率同樣是fmb、fm1和fm2，但還出現一些高頻成分，如3fm1、11fm2和16fm2。

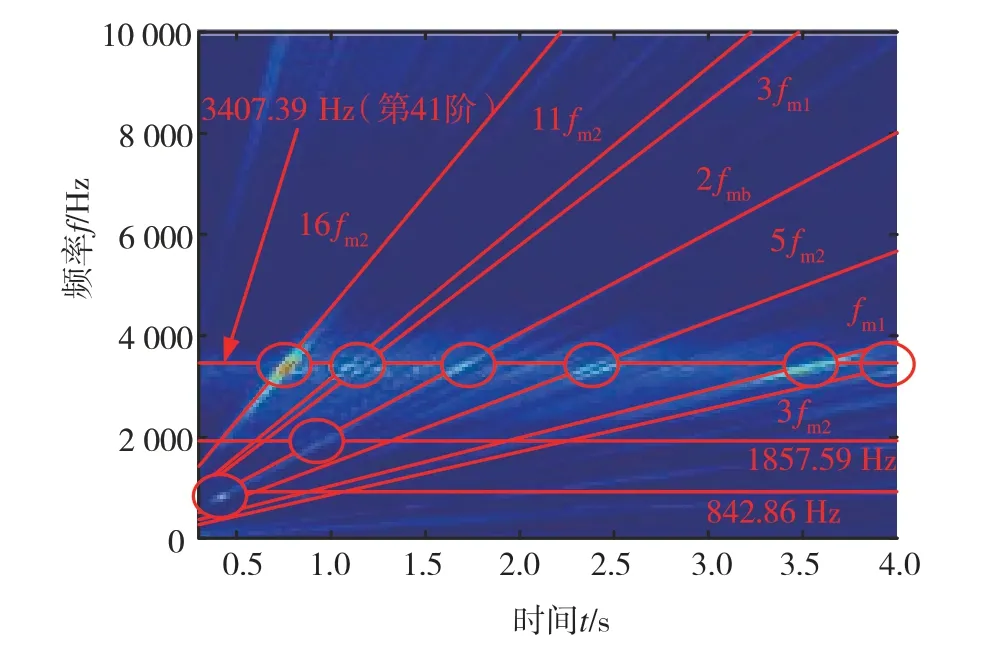
圖31 一級齒輪副動態嚙合力矩時頻圖

齒輪誤差對系統共振影響的結果如表3所示，本文只給出了最危險的3個電機轉速及其對應的共振頻率。分析可知，考慮齒輪誤差后時頻圖的頻率成分更加復雜，出現一些由齒輪嚙合頻率的高倍頻如3fm1、11fm2和16fm2引起的共振，且主要共振轉速也發生改變。這是因為齒輪誤差的頻率成分復雜，頻率分布范圍廣，更容易激發系統共振。從表3還可以看出第41階固有頻率3 407.39 Hz比較容易被激發，應重點關注。

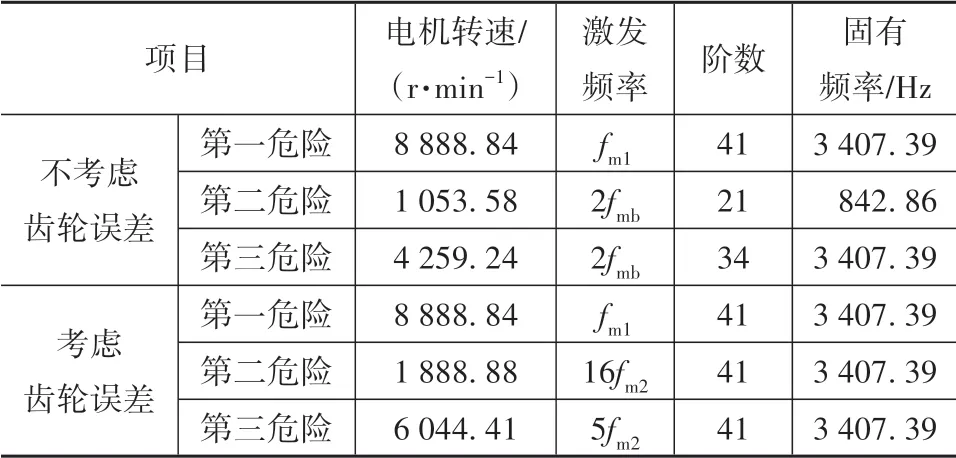
表3 齒輪誤差對系統共振影響

3.2 加速工況下耦合系統共振分析

3.2.1 耦合系統特征值計算

圖32為耦合箱體前后系統前80階固有頻率對比，可以看出耦合箱體后系統固有頻率明顯降低，這是因為耦合箱體后系統的柔性增加。

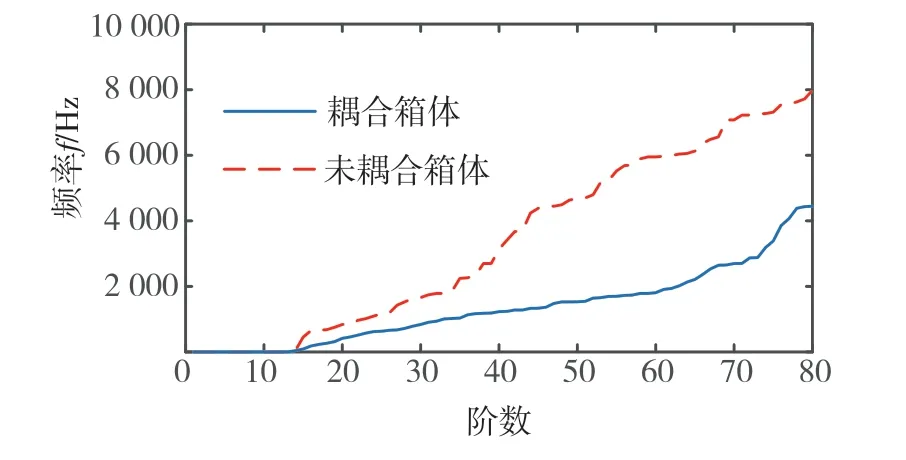
圖32 固有頻率對比

表4為耦合箱體下，虛部絕對值大于零的部分階數特征值。

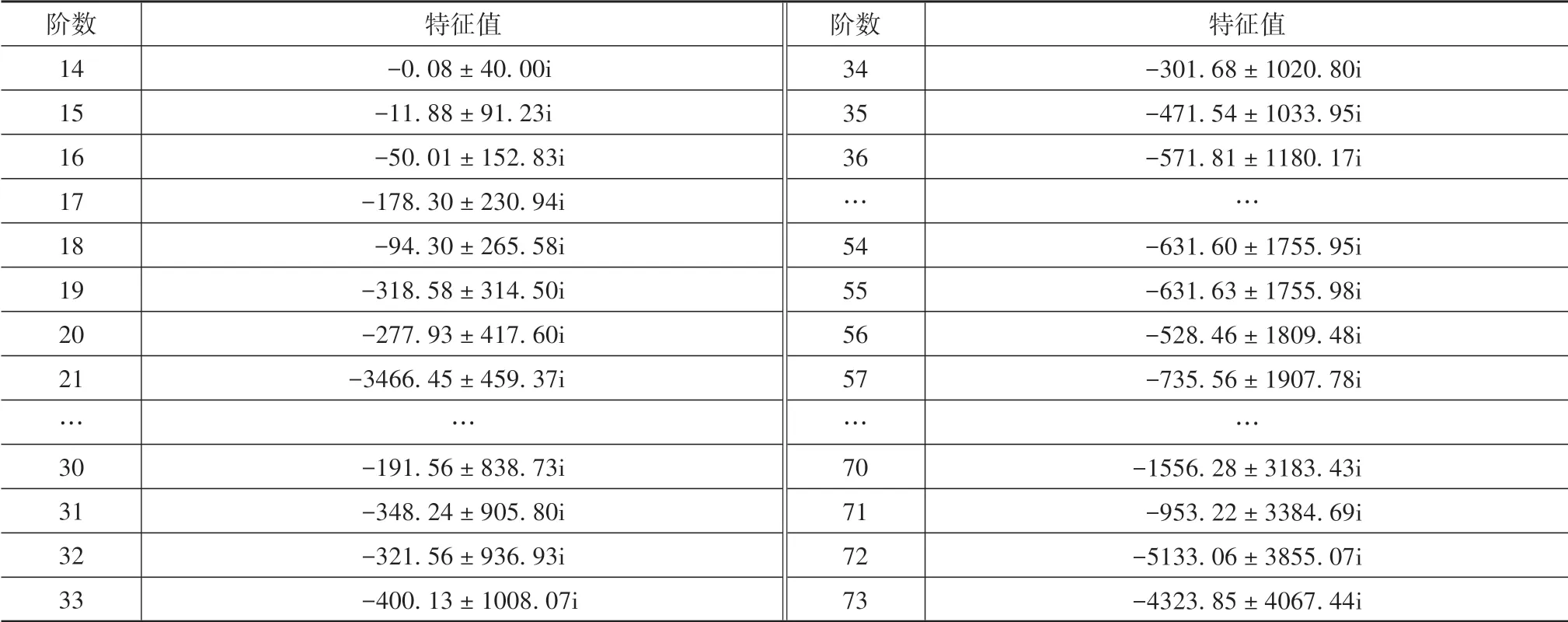
表4 耦合箱體下系統特征值

3.2.2 耦合系統共振分析

圖33為耦合箱體前后一級齒輪副動態嚙合力矩的時域圖。可以看出：耦合箱體前后前3個主共振峰幅值波動的差異不大；但耦合箱體后，動態嚙合力矩在3.7 s左右波動幅值明顯變大。

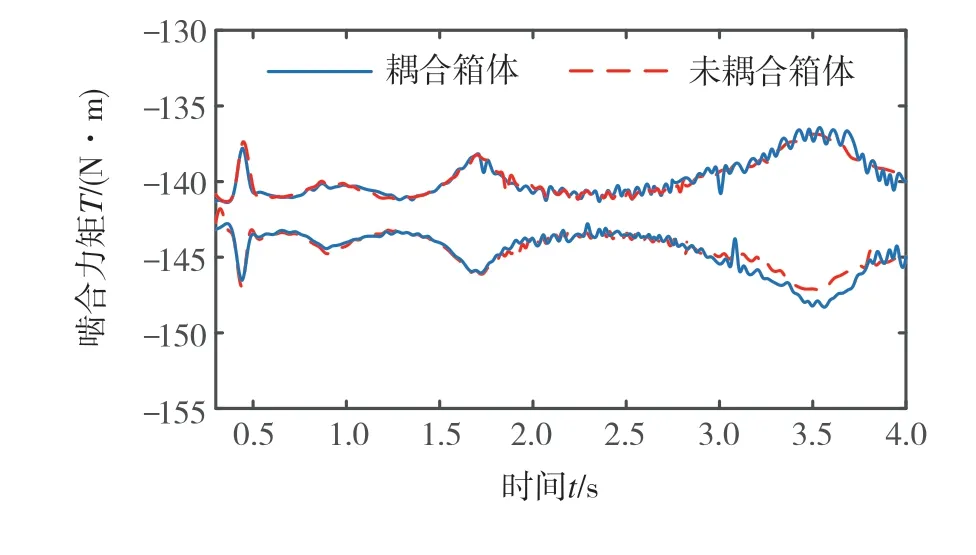
圖33 一級齒輪副齒輪動態嚙合力矩

圖34為耦合箱體后一級齒輪副動態嚙合力矩的時頻圖。可以看出，導致系統發生共振的激勵頻率主要為fmb、fm1和fm2，同時還出現了由電機轉頻fr1引起的共振。箱體對系統共振影響的結果如表5所示。

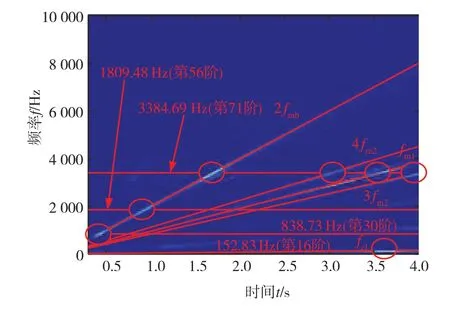
圖34 一級齒輪副動態嚙合力矩時頻圖

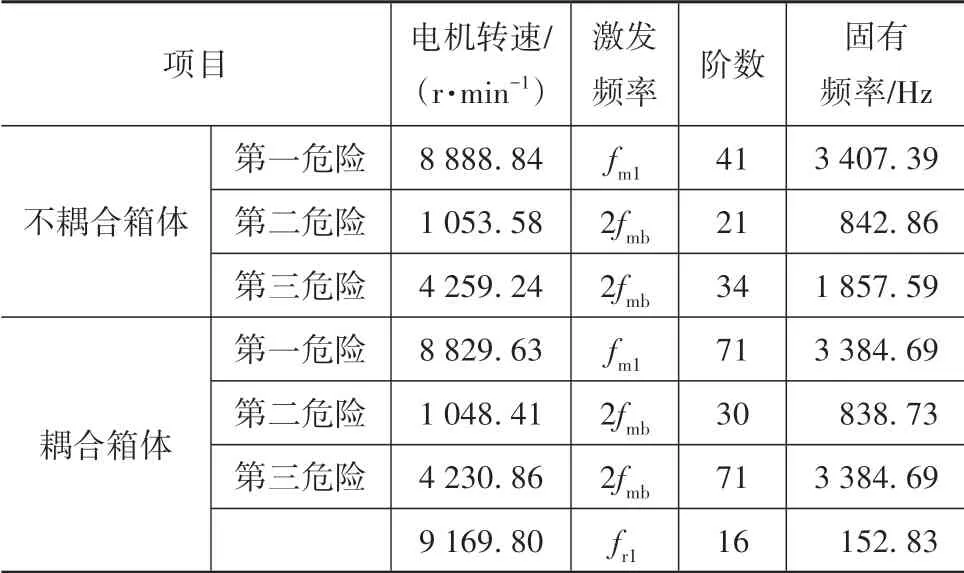
表5 箱體對系統共振影響

對比耦合箱體前后系統的共振轉速和共振頻率，發現耦合箱體后系統共振轉速和共振頻率都有所降低。這是因為引入箱體柔性后，系統的固有頻率降低，導致共振頻率和共振轉速均降低。對比表2和表3發現，耦合箱體后出現了原來沒有的頻率成分152.83 Hz，該頻率為計入箱體后的模態頻率。當電機轉速為9 169.80 r/min時，轉頻fr1激發了耦合箱體后系統的第16階固有頻率152.83 Hz，導致3.7 s左右齒輪嚙合力矩波動幅值明顯變大，同時該轉速下fm1激發了系統第71階固有頻率，出現了2階固有頻率共同作用的共振現象，該現象將結合圖35進行討論。

下面將從軸承動態支反力的角度驗證上述結論。圖35為耦合箱體前后軸承2的動態支反力時域圖。可以看到在3.7 s時耦合箱體后的軸承力幅值顯著增大，出現了明顯的共振峰，這表明耦合箱體后系統在該共振峰對應的轉速附近發生了共振，主要激勵頻率為fr1。綜上分析可得：耦合箱體后電驅動系統的共振轉速和共振固有頻率均降低，且容易激發與轉頻相關的低階共振。

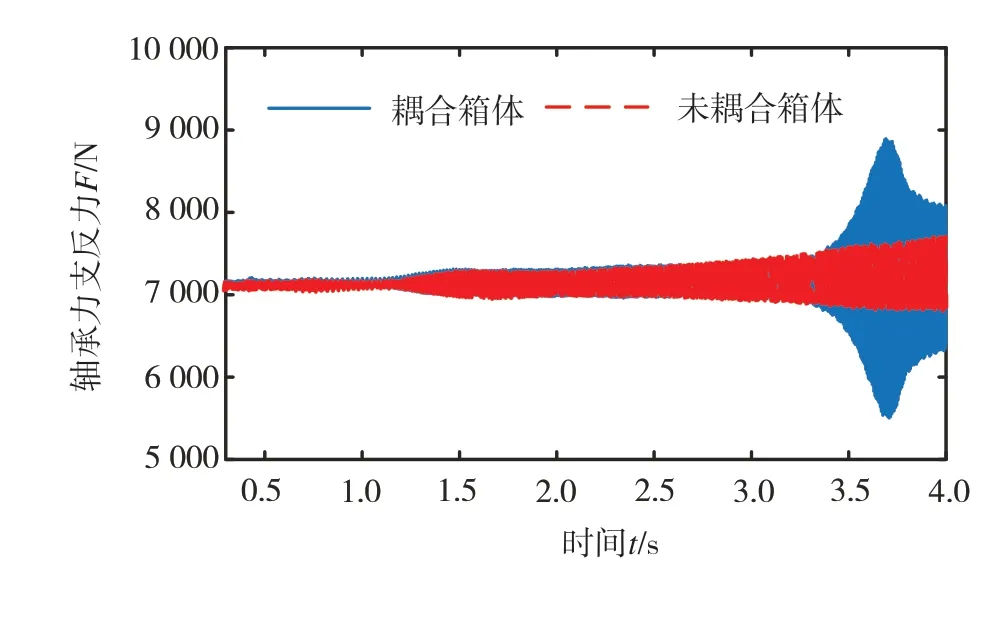
圖35 軸承2動態支反力

4 結論

本文以純電動汽車電驅動系統為對象，建立了一種適用于變速工況且考慮電磁力時空分布和系統結構柔性的一體化電驅動系統機電耦合動力學模型，分析了在穩態和加速工況下電機轉矩波動、齒輪誤差和箱體柔性對系統動態特性的影響規律。

（1）穩態工況下電機波動轉矩、齒輪誤差、柔性箱體對系統動力學特性的影響體現在：電機轉矩波動會增大齒輪動態嚙合力矩的幅值，對距離電機較近位置處的嚙合副影響顯著，較遠位置處的嚙合副影響較小，但電機轉矩波動對軸承力的影響不明顯；齒輪誤差會顯著增加齒輪動態嚙合力矩和軸承支反力的幅值；齒輪誤差的高頻成分對軸承支反力的影響不大；箱體柔性對齒輪動態嚙合力矩的影響較小，箱體對軸承支反力的影響顯著，但不同位置處的影響效果不同。

（2）加速工況下進行了共振分析，研究了齒輪誤差和箱體對系統動力學特性的影響：導致系統共振的頻率主要包括電機轉矩頻率fmb、齒輪副嚙合頻率fm1和fm2，齒輪誤差容易激起系統高頻成分的共振，如3fm1、11fm2和16fm2；耦合箱體后電驅動系統的固有頻率顯著降低，并且共振轉速和固有頻率均降低，耦合箱體后容易激發與轉頻相關的低階共振。