基于遺傳算法優化BP神經網絡的集裝箱吞吐量預測

0 引言

集裝箱運輸具有減少貨損貨差率、綠色環保、提高裝卸效率、可多式聯運等優點，集裝箱運輸逐漸取代了傳統的散貨運輸方式，成為主要貿易運輸方式[1-2]。

根據交通運輸部統計，2021年全國港口集裝箱吞吐量達2.83億TEU，在新冠疫情影響下實現逆勢同比增長7.0%。在集裝箱運輸蓬勃發展的同時，伴隨而來的是港口建設產能過剩、資源配置效率低等問題[3]。港口的需求是港口投資建設與運營的重要依據[4]，而港口基礎投資具有高風險、不可逆轉的性質[5]，因此準確的對港口集裝箱吞吐量需求進行預測對提高港口投資效率、指導港口發展方向、規劃港口整體布局、制定日常生產作業計劃具有重要意義。

自20世紀80年代以來，集裝箱吞吐量預測是一個比較熱門的研究領域，目前國內外學者針對港口集裝箱吞吐量預測的主要方法可分為單一模型和混合模型[6]。單一模型又可分為時間序列模型和非線性模型[7]，時間序列模型如指數平滑（Exponential Smoothing,ES）、季節性自回歸綜合移動平均（Seasonal Autoregressive Integrated Moving Average Model,SARIMA）和灰色預測模型（Grey Forecasting Model,GM）等。例如，陳寧等[8]提出利用對數二次指數平滑方法預測港口吞吐量，結果表明對數二次指數平滑方法適用于快速成長的港口的吞吐量預測。Ghaderi等[9]應用ES方法對澳大利亞主要港口集裝箱吞吐量的變化趨勢進行預測。王向前等[10]提出一個ARIMAX-SVR預測方法對天津港吞吐量進行預測，改進后的模型精度為0.43%，提高了預測精度。董潔霜等[11]采用SARIMA模型對上海港集裝箱吞吐量的季節性變化規律進行分析，并給出月度數據預測值。上述模型大多基于線性假設,不能很好地刻畫原始數據中的非線性特征，集裝箱吞吐量受到腹地經濟、政策環境等因素的影響,其時間序列具有高度非線性[7,12]。隨著計算機技術的進步，逐漸開發出人工智能技術為基礎的非線性模型，主要包括反向傳播（Back Propagation,BP）神經網絡、遺傳規劃（GP）和支持向量機（SVM）。如吳利清[13]以歷史前三年的集裝箱吞吐量作為輸入樣本建立BP神經網絡預測模型并對驗證集進行驗證發現精度良好，驗證模型可行性后對福州港集裝箱吞吐量進行預測。Tang等[14]在分析上海港和連云港的集裝箱吞吐量變化時,發現BP模型的預測效果優于GM、三重指數平滑和多元線性回歸等時間序列模型。黃安強等[15]首次將遺傳規劃算法（GP）應用于集成預測問題的研究，并使用最小二乘估計算法（LSE）對經典遺傳規劃算法進行改進預測青島港集裝箱吞吐量，結果表明基于GP-LSE的非線性集成預測方法在預測數值準確度和方向準確度兩個維度都顯著優于時間序列模型。宋長利等[16]構建了基于支持向量機模型的多步混合預測方法，并通過對大連港66個月吞吐量樣本數據進行了實證分析，結果表明集裝箱的預測值與實際值的平均相對誤差為2.8%。

集裝箱吞吐量受眾多因素影響，由于單一模型方法本身的限制，單一模型存在各種缺陷。眾多學者提出使用各種混合模型進行預測，如李長安等[17]為提高模型精度，通過蟻群算法優化BP神經網絡后進行預測，結果表明混合模型的精度優于其他單一模型。高偉等[18]通過熵值法確定各指標的影響權重，結合BP神經網絡方法對機場旅客吞吐量進行預測，證明上述方法可減小誤差。謝新連等[19]建立基于隨機森林（Random Forest,RF）算法的預測模型，以大連港為案例進行驗證，并與三次指數平滑、多元回歸分析和BP神經網絡三種方法預測進行對比，結果表明隨機森林算法預測準確性更高。孫曉聰等[20]提出基于隨機森林與雙向長短期記憶網絡（Long Short-Term Memory Network,LSTM）結合的集裝箱吞吐量預測方法對青島港集裝箱吞吐量進行預測，結果顯示RF-雙向LSTM預測精度顯著高于其他模型。He和Wang[21]將GM 1,()1和BP神經網絡相結合結果表明，組合模型分別優于其他單一模型，具有更高的預測精度。

BP神經網絡具有良好的非線性擬合能力，適合應用于集裝箱吞吐量預測[22]。但網絡輸入變量的合理選擇對預測效果至關重要。目前在使用BP神經網絡進行集裝箱吞吐量的預測研究中，大部分學者使用歷史集裝箱吞吐量作為輸入變量進行預測，如吳利清、陳錦文、曹杰等人[13,23-24]均采用歷史集裝箱吞吐量數據作為輸入變量進行預測。影響集裝箱吞吐量的重要因素同時還應包括腹地GDP和腹地貨運量[25]，等等。本文采用歷史前三年集裝箱吞吐量、腹地GDP、腹地貨運量作為輸入變量，遺傳算法適用于解決復雜的非線性和多維空間尋優問題[26]，利用遺傳算法（GA）來彌補BP神經網絡連接權值和閾值選擇上的隨機性缺陷，建立GA-BP預測模型。

1 遺傳算法優化的BP神經網絡

1.1 BP神經網絡

BP神經網絡是一種按照誤差逆向傳播算法訓練的多層前饋神經網絡。BP神經網絡能學習和存貯大量的輸入輸出模式映射關系，網絡由輸入層、隱含層、輸出層組成，其結構如圖1所示。

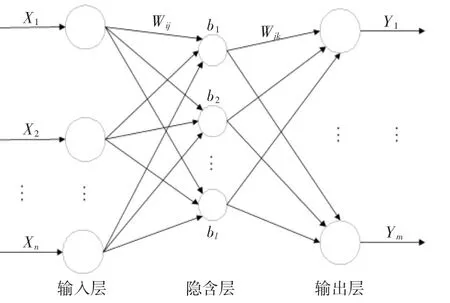
圖1 BP神經網絡結構圖

圖1中，X1,X2,…,Xn是網絡的輸入；Y1,Y2,…,Ym是網絡的輸出；Wij和Wjk是網絡的權值；l是隱藏神經元的個數。目前如何設置隱含層神經元個數沒有完整的理論指導，依靠經驗公式[27]試驗確定。

式（1）中：m為輸入層節點個數，n為輸出層節點個數，a是自取的任意值，一般范圍在1到10之間；b1,b2…,bn是網絡的閾值。

BP神經網絡的主要特點是信號前向傳播，誤差反向傳播。設定期望輸出值，網絡根據預測輸出與期望輸出的誤差對比結果進行反向傳播，調整各神經元的權值和閾值。整個過程反復進行，直到網絡樣本輸出誤差E＜ε（ε為期望誤差精度）或訓練達到最大迭代次數為止。

1.2 遺傳算法

遺傳算法是模擬自然界生物進化機制的一種算法。在遺傳算法中，通過編碼組成初始群體后，遺傳操作對群體的個體按照它們對環境適應度施加一定的操作，從而實現優勝劣汰的進化過程。從優化搜索的角度而言，遺傳操作可使問題的解一代又一代地優化，并逼近最優解。遺傳操作包括以下三個基本操作：選擇、交叉和變異。

（1）選擇

從群體中選擇優勝的個體，淘汰劣質個體的操作叫選擇。輪盤賭選擇法是最簡單也是最常用的選擇方法，在該方法中個體的選擇概率與其適應度值成比例。設群體大小為n，其中個體i的適應度為fi，則i被選擇的概率為：

（2）交叉

交叉是指把兩個父代個體的部分結構加以替換重組而生成新的個體的操作。

（3）變異

變異的基本內容是對群體中的個體串的某些基因座上的基因值做變動產生新的個體。

1.3 GA-BP模型

遺傳算法優化BP神經網絡的步驟如下：

（1）確定BP神經網絡拓撲結構從而確定網絡的權值和閾值數。

（2）設定GA的相關網絡參數。

（3）GA初始值編碼并根據BP網絡訓練誤差進行迭代。

（4）用GA迭代得到最優個體并賦值給BP神經網絡，運行BP神經網絡得到預測結果。

遺傳算法優化BP神經網絡的流程如圖2所示。

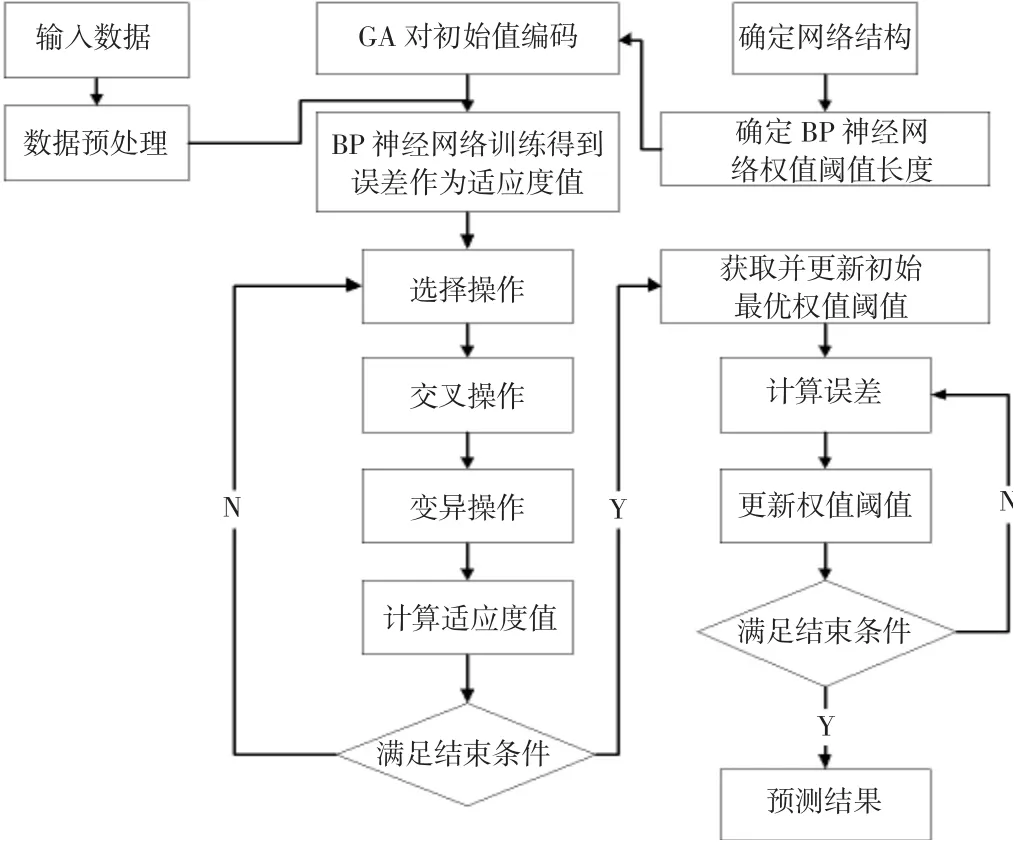
圖2 GA-BP神經網絡流程圖

2 集裝箱吞吐量預測

2.1 數據預處理

選取福州港2008—2020年的腹地GDP、腹地貨運量、歷史前三年的吞吐量數據作為訓練樣本，考慮數據樣本較少，同時設定2008—2020年的相關數據為測試樣本，以便進行驗證。根據姜云飛的研究[28]，福州港腹地GDP=（福州GDP）*95%+（三明GDP）*25%+（南平GDP）*25%+（寧德GDP）*20%+（莆田GDP）*10%。具體數據如表1所示。

表1中，X1為腹地GDP（單位：億元），X2為腹地貨運量（單位：萬噸），X3為當年的前三年集裝箱吞吐量（單位：萬TEU），X4為當年的前2年集裝箱吞吐量（單位：萬TEU），X5為當年的前1年集裝箱吞吐量（單位：萬TEU）。Yi為當年實際集裝箱吞吐量（單位：萬TEU）。

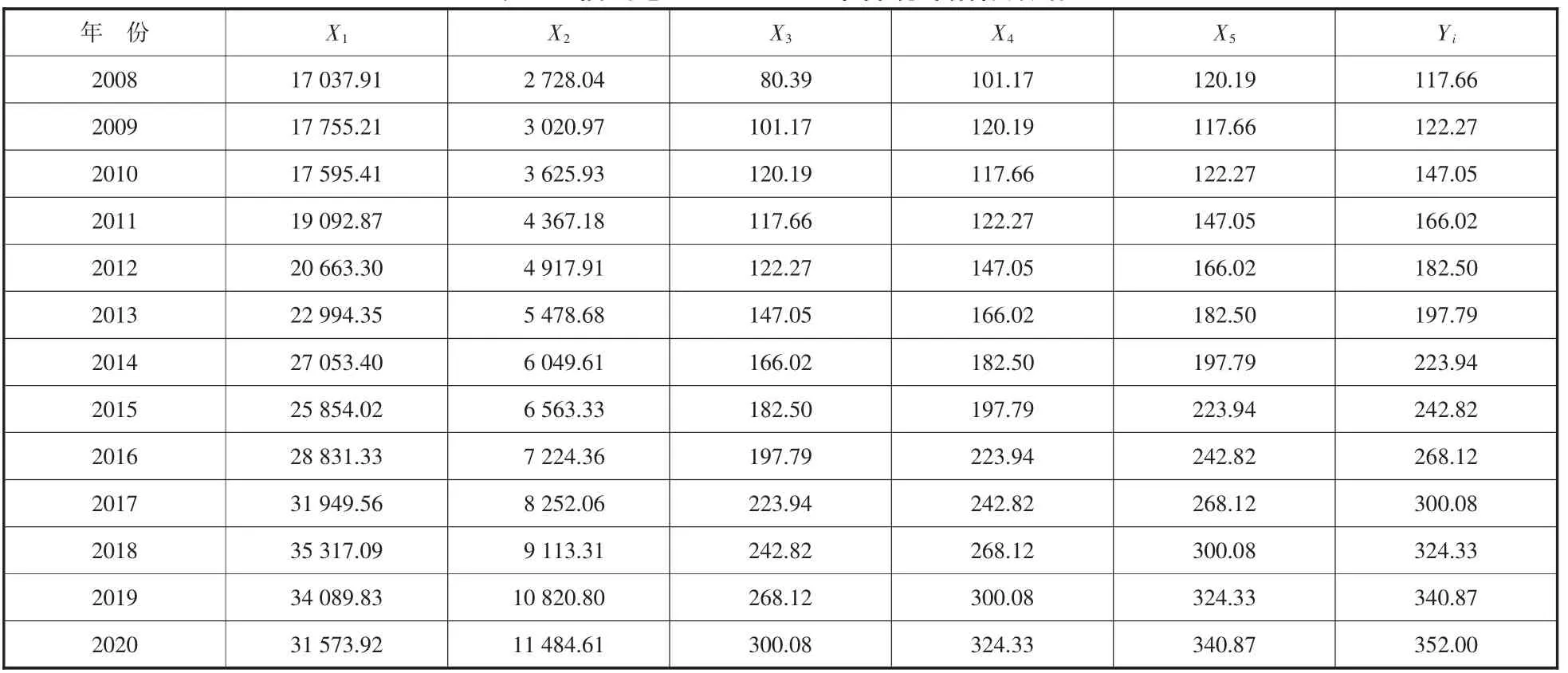
表1 福州港2008—2018年各統計指標數據

2.2 網絡參數的設置

遺傳算法相關參數：初始種群規模為30，最大進化代數為50，交叉概率為0.8，變異概率為0.2。

BP神經網絡相關參數：最大訓練次數為1 000，學習速率為0.01，學習最小誤差為1×10-6，采用3層結構的網絡進行訓練，輸入層節點為5，輸出層節點為1，根據試驗法確定隱含層神經元個數，經過大量訓練，隱含層神經元個數為4時訓練效果較好。

2.3 評價指標

本文選取MAE和MAPE作為模型的評價指標：

其中：m為測試集的個數，xi、yi分別為預測值與實際值。

2.4 仿真結果

通過Matlab R2019a軟件仿真，2008—2020年福州港集裝箱實際吞吐量、BP神經網絡預測值與GA-BP網絡預測值以及預測相對誤差如表2、圖3所示。

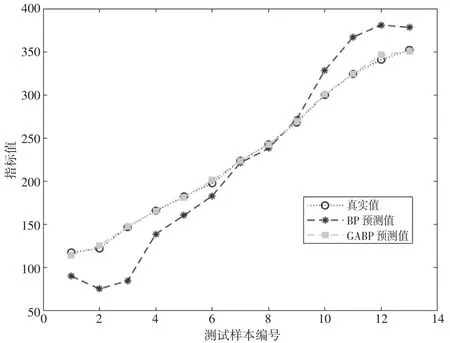
圖3 BP神經網絡與GA-BP預測值對比

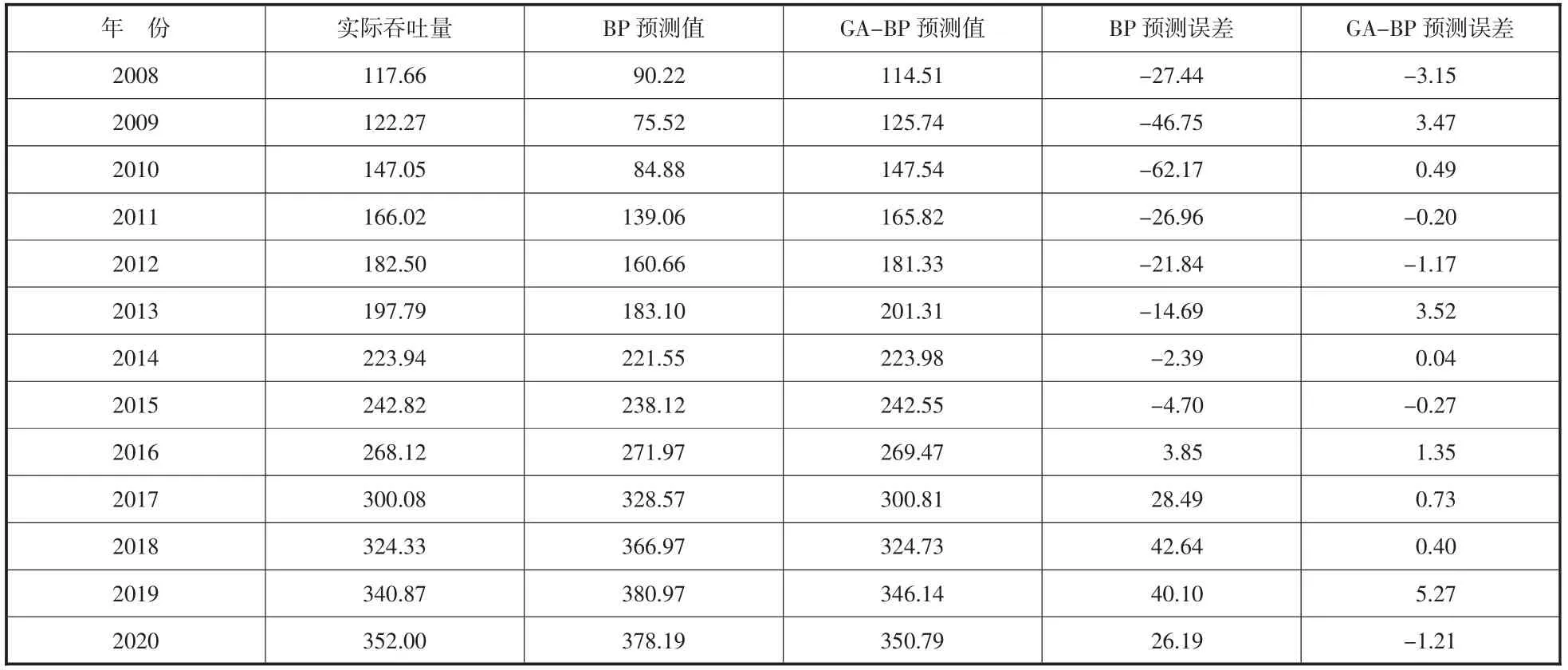
表2 福州港2008—2020年預測值對比

通過測試樣本的仿真結果，BP神經網絡平均絕對誤差MAE為26.78，GA-BP模型平均絕對誤差MAE為1.636，BP神經網絡平均絕對百分比誤差MAPE為14.28%，GA-BP模型平均絕對百分比誤差MAPE為0.87%，表明GA-BP模型精度更高，同時對比吳利清[13]以歷史集裝箱吞吐量為輸入變量對福州港2012—2020集裝箱吞吐量的驗證集預測，MAE和MAPE分別為6.27和2.1%，本文同時期測試集的MAE和MAPE分別為1.55和0.59%，顯著低于其結果，表明本文的輸入變量更合理。

2.5 集裝箱吞吐量預測

通過測試集的仿真結果，驗證了GA-BP模型進行預測的有效性。根據前文建立的GA-BP預測模型對福州港2021—2025年集裝箱吞吐量進行預測。首先采用線性回歸預測方法預測腹地貨運量，其擬合函數及R2值如圖4所示。

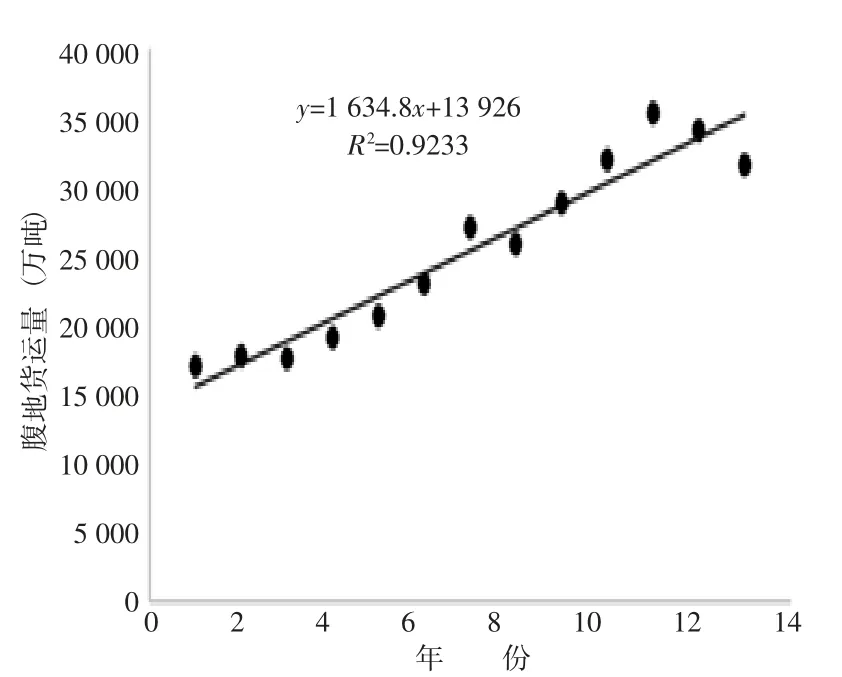
圖4 線性回歸方法預測腹地貨運量

根據所得線性擬合函數預測歷年貨運量值如表3所示。

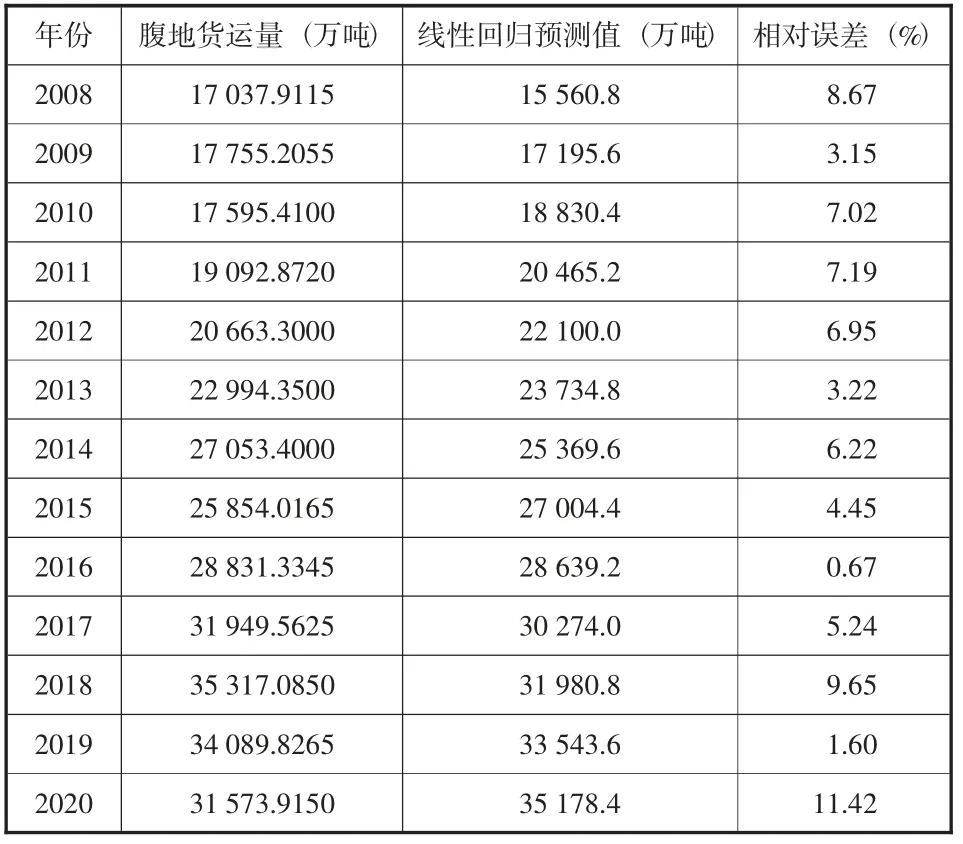
表3 線性回歸方法預測腹地貨運量

分析線性擬合函數的結果，平均相對誤差MAPE為5.8%，效果良好。同時采用指數回歸預測方法預測腹地GDP，其擬合函數及R2值如圖5所示。

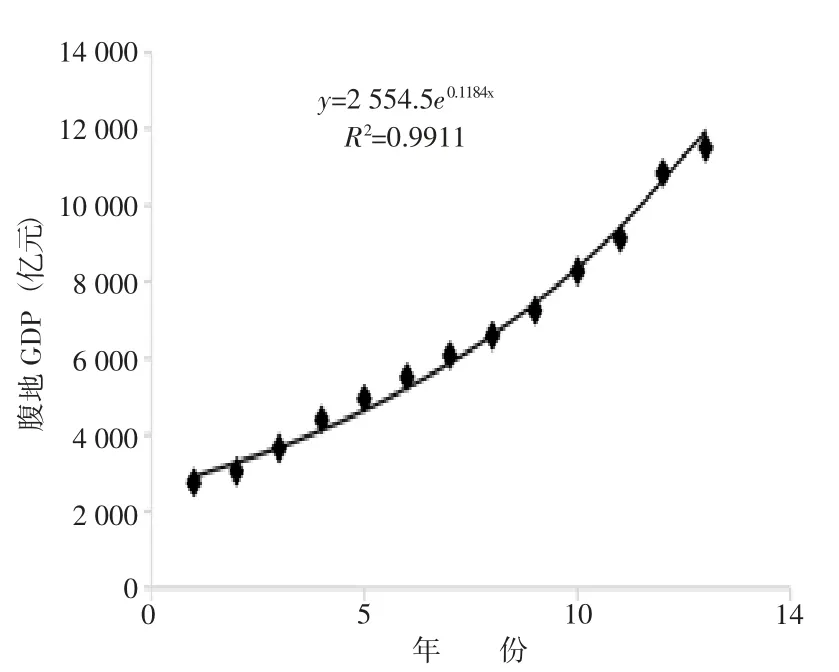
圖5 指數回歸方法預測腹地GDP

根據所得指數擬合函數預測歷年GDP如表4所示。

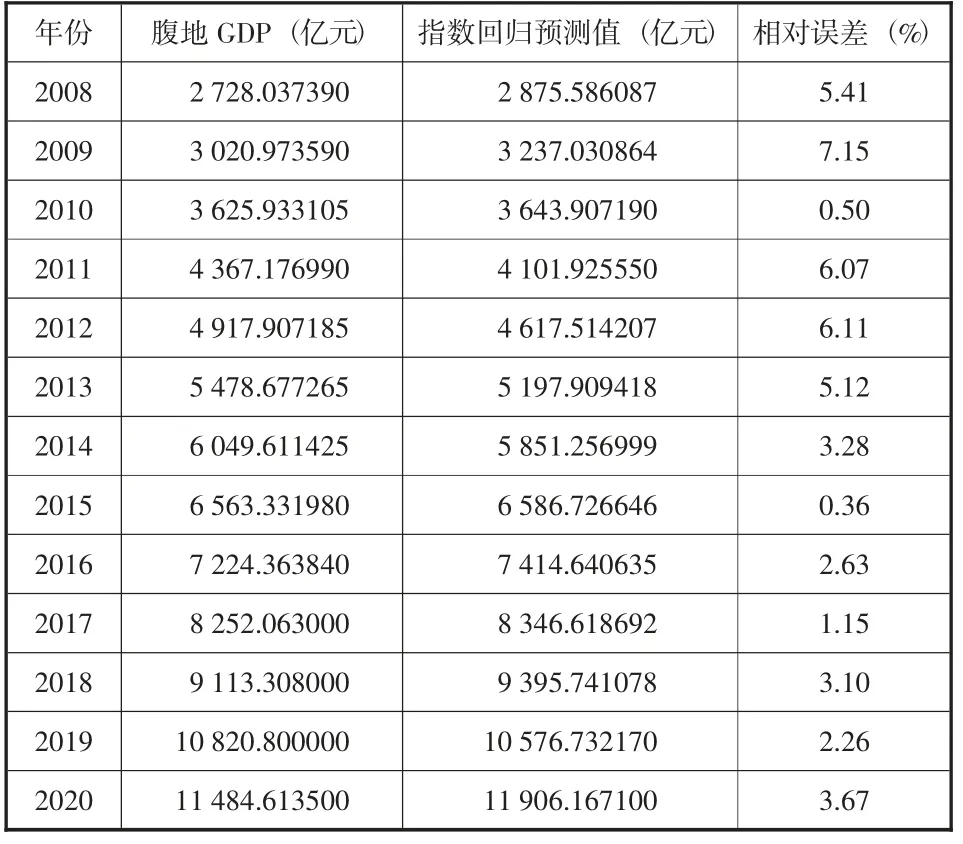
表4 指數回歸方法預測腹地GDP

分析指數擬合函數的結果，平均相對誤差MAPE為3.6%。由此得到2021—2025年福州港腹地貨運量與腹地GDP如表5所示。

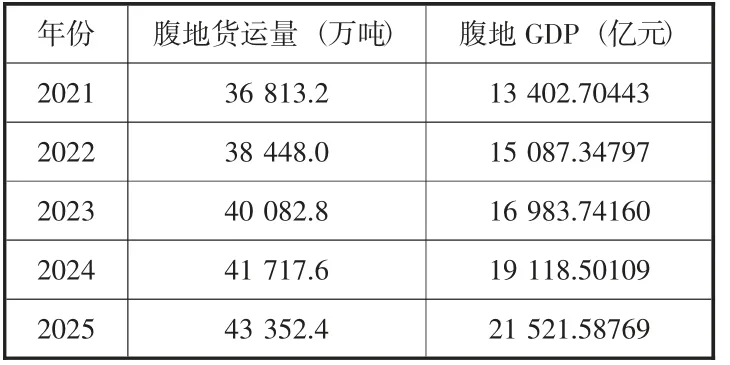
表5 2021—2025年腹地貨運量與腹地GDP預測值

利用GA-BP預測模型預測各年的集裝箱吞吐量，預測數據及過程如表6所示。

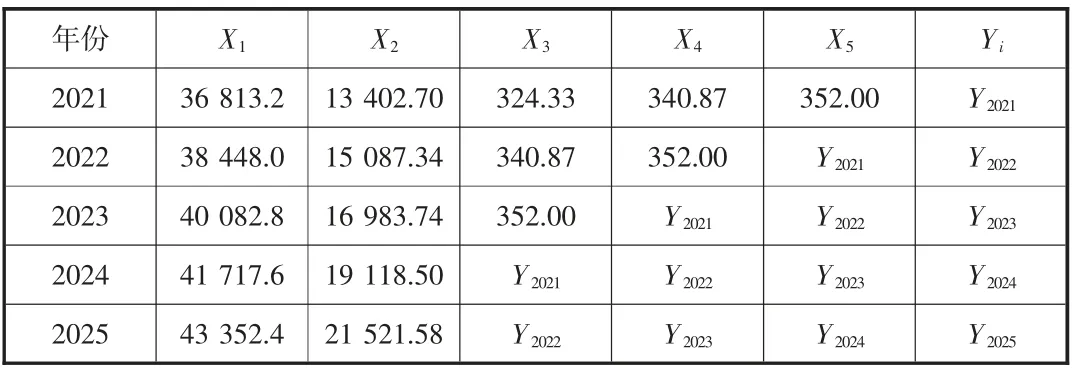
表6 2021—2025年福州港集裝箱吞吐量預測

其中：Yi分別為2021—2025年GA-BP模型的集裝箱吞吐量預測值。通過Matlab R2019a仿真，福州港2021—2025年集裝箱吞吐量預測值如表7所示。

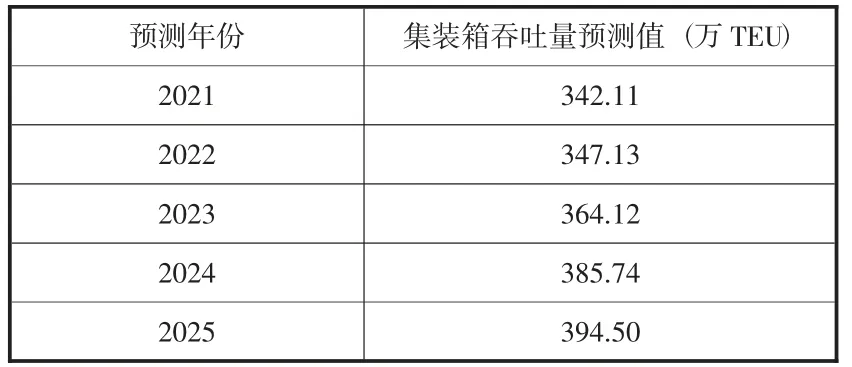
表7 2021—2025年福州港集裝箱吞吐量預測值

2021年福州港實際集裝箱吞吐量為345萬TEU，預測值為342.11萬TEU，再次驗證了預測模型的有效性。

3 結束語

本文通過提出腹地GDP、腹地貨運量、歷史前三年的集裝箱吞吐量作為網絡輸入建立了BP神經網絡預測模型，并利用遺傳算法優化BP神經網絡的初始權值和閾值，從而建立了GA-BP預測模型并進行了驗證和預測。通過仿真結果表明，與BP神經網絡和以歷史集裝箱吞吐量數據為輸入相比，本文基于腹地GDP、腹地貨運量、歷史前三年的集裝箱吞吐量建立的GA-BP預測模型具備更高的預測精度和合理性，為港口集裝箱吞吐量預測提供了一定的參考。