武夷山丘陵茶園紅壤土壤可蝕性近似計(jì)算初探
楊辰叢海, 陳志強(qiáng)
(福建師范大學(xué) 地理科學(xué)學(xué)院, 福州 350107)
土壤侵蝕指土壤及其母質(zhì)在外營力作用下被破壞、剝蝕、搬運(yùn)及堆積的過程,是人類面臨的最普遍、持續(xù)性最強(qiáng)的一種地質(zhì)災(zāi)害[1]。持續(xù)的土壤侵蝕對(duì)社會(huì)經(jīng)濟(jì)發(fā)展、農(nóng)業(yè)耕作發(fā)展及生態(tài)環(huán)境保護(hù)均會(huì)造成不利影響[2]。土壤可蝕性因子K值是土壤侵蝕的內(nèi)營力因素,其反映土壤對(duì)外界外營力剝蝕與搬運(yùn)的敏感性[3],是土壤侵蝕模型中的重要參數(shù),與土壤侵蝕嚴(yán)重程度呈正相關(guān)關(guān)系,其值越高則代表土壤抗沖蝕能力越弱,被侵蝕的可能性越強(qiáng)[4]。分析土壤可蝕性,可準(zhǔn)確進(jìn)行水土流失預(yù)報(bào),評(píng)價(jià)土地生產(chǎn)力[5]。
國內(nèi)外土壤可蝕性因子研究始于20世紀(jì)30年代。Bouyoucos[6]、Middleton[7]等眾多學(xué)者通過分析土壤粒徑分布、化學(xué)組成、滲水率等因素提出不同角度土壤可蝕性定量化方法。Wischmeier等[8]通過人工降雨模擬侵蝕,選定土壤指標(biāo)進(jìn)行回歸分析,得出土壤可蝕性因子經(jīng)驗(yàn)計(jì)算方程。美國水土保持局提出的通用土壤流失方程(Universal Soil Loss Equation,USLE)及其修正形式(RUSLE),廣泛運(yùn)用于水土流失預(yù)報(bào)[9]。1984年Williams等[10]從土壤不同粒級(jí)機(jī)械組成百分比出發(fā)提出的土壤侵蝕—土地生產(chǎn)力可蝕性計(jì)算模型(Erosion-Productivity Impact Calculator,EPIC),因其測(cè)量的便捷性、可比性與定量化,成為我國學(xué)者計(jì)算土壤可蝕性因子K值較為主流的方法之一。近年來,F(xiàn)arshad Kiani[11]、Selen Deviren[12]等對(duì)伊朗、土耳其等地區(qū)土壤進(jìn)行研究,發(fā)現(xiàn)干旱區(qū)土壤K值影響因素往往更為復(fù)雜。在我國,楊玉盛等[13]將土壤分散特性、團(tuán)粒結(jié)構(gòu)特性等引入土壤可蝕性因素進(jìn)行考慮;朱顯謨[14]基于黃土高原特性,對(duì)當(dāng)?shù)赝寥揽箾_性與滲透性進(jìn)行研究。基于土壤可蝕性定量化研究方法,眾多學(xué)者對(duì)中國不同地區(qū)土壤可蝕性開展了大量研究,研究成果頗豐。然而,現(xiàn)有土壤可蝕性因子計(jì)算存在計(jì)算過程繁瑣,所需數(shù)據(jù)較多的缺憾。就相對(duì)簡(jiǎn)單且經(jīng)典EPIC模型而言,方程內(nèi)有砂粒、粉粒、黏粒及有機(jī)碳含量4種自變量,利用其計(jì)算可蝕性,需測(cè)定對(duì)應(yīng)的4種參數(shù),在實(shí)驗(yàn)室條件較差的情況下,測(cè)量相關(guān)參數(shù)特別是有機(jī)碳含量難度大,且若以常用的沉降法測(cè)量機(jī)械組成,要測(cè)得粒徑細(xì)小的黏粒,需靜置沉降等待約7 h(20℃)[15],時(shí)間成本較高。砂粒是土壤中粒徑最大的部分,在野外通過干測(cè)法就可估算其大致百分比含量,且在實(shí)驗(yàn)室中,砂粒沉降僅需1 min左右,沉降速度快,遠(yuǎn)低于黏粒沉降時(shí)間。若針對(duì)某一特定地區(qū)土壤質(zhì)地特點(diǎn),建立相關(guān)擬合方程,通過某一粒級(jí)含量求出對(duì)應(yīng)地區(qū)土壤可蝕性K值的近似值,將大大方便其計(jì)算及可蝕性的戶外比較,節(jié)省時(shí)間成本。然而,對(duì)通過土壤中某一粒級(jí)含量求取可蝕性K值近似值的研究尚屬少見。
本文以福建省武夷山市為研究區(qū)域,利用EPIC公式定量化計(jì)算武夷山丘陵地區(qū)典型茶園土壤可蝕性K值大小,并求取不同粒級(jí)土粒含量百分比與K值的相關(guān)關(guān)系,探討擬合建立單變量近似方程以求出近似K值的途徑,以期為武夷山市茶園紅壤提供簡(jiǎn)便且較精確的K值計(jì)算方法,助力水土保持及土壤侵蝕研究工作的開展。
1 研究區(qū)概況
武夷山市隸屬福建省南平市,位于閩贛交界部位,經(jīng)緯度為北緯27°27′—28°04′,東經(jīng)117°37′—118°19′。武夷山山脈平均海拔高度1 000~1 100 m,地勢(shì)起伏大[16],隨著海拔上升,土壤垂直分異明顯,丘陵地區(qū)地帶性土壤為紅壤。區(qū)內(nèi)屬亞熱帶季風(fēng)氣候,夏季炎熱多雨,冬季溫和少雨,年均溫約18.9℃[17],年降水量約2 000 mm,相對(duì)濕度85%。茶業(yè)是武夷山市支柱性產(chǎn)業(yè),在其經(jīng)濟(jì)發(fā)展中具有不可替代的作用。2018年,全市茶園面積達(dá)98.6 km2,產(chǎn)值21.12億元,涉茶人口達(dá)8萬人,占全市人口的34%[18],武夷巖茶享譽(yù)全球,其中武夷大紅袍更是中國十大名茶之一[19]。因森林覆蓋率高,武夷山市土壤侵蝕現(xiàn)狀尚不嚴(yán)重,土壤保持量高,但由于山地內(nèi)部海拔高、部分地區(qū)植被覆蓋度差、降水侵蝕性高及潛在的茶園土壤酸化等因素[20],土壤可蝕性在部分地區(qū)較高,有發(fā)生嚴(yán)重水土流失的可能。
2 材料與方法
2.1 數(shù)據(jù)來源
本文土壤有關(guān)數(shù)據(jù)來源于2020年10月戶外采集的武夷山星村、溪前、黃坑、黃溪口茶園紅壤16個(gè)樣點(diǎn)共32組土樣數(shù)據(jù),均位于海拔小于500 m,即250 m左右的丘陵地區(qū)。按土樣深度、剖面特征及耕作程度分為耕作層及非耕作層,耕作層長期受人類耕作活動(dòng)影響,非耕作層受人類活動(dòng)影響相對(duì)較小,在實(shí)際采樣中,以是否可明顯觀察到植物根系作為劃分耕作層與非耕作層的依據(jù),可明顯觀察到根系為耕作層。采集耕作層土樣16組,非耕作層土樣16組,全部為紅壤,是當(dāng)?shù)厍鹆甑貐^(qū)茶葉種植的代表性土壤。為方便表述,在下文中,以“M層”指代耕作層,“N層”指代非耕作層。
2.2 研究方法
2.2.1K值計(jì)算與擬合方法 本研究中,土壤機(jī)械組成由沉降法測(cè)定,pH值采用電位法測(cè)定,土壤有機(jī)碳含量以丘林法測(cè)定,見公式(1)。
(1)
可蝕性因子K值計(jì)算采用Williams等[10]在EPIC模型中提出的土壤侵蝕方程經(jīng)驗(yàn)公式(2),粒徑分級(jí)按美國農(nóng)部制分級(jí)法,0.05~2 mm為砂粒(SAN),0.002~0.05 mm為粉粒(SIL),0.002 mm以下為黏粒(CLA)。
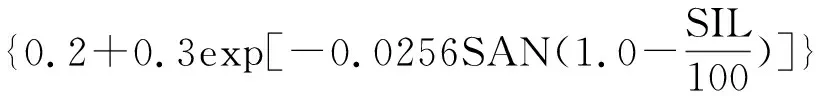
(2)
式中:SAN,SIL,CLA及C分別代表砂粒、粉粒、黏粒及有機(jī)碳含量(%),SNI=1—SAN/100。據(jù)公式(2)計(jì)算得武夷山丘陵茶園紅壤K值。
計(jì)算得K值后,將相關(guān)系數(shù)高、相關(guān)性較顯著的粒級(jí)作為自變量,K值作為因變量,采用最小二乘法作為基本擬合方法,導(dǎo)入MATLAB進(jìn)行線性最小二乘直線擬合及非線性最小二乘曲線擬合。為防止擬合多項(xiàng)式次數(shù)過高而產(chǎn)生rouge現(xiàn)象,非線性最小二乘使用冪函數(shù)及二次多項(xiàng)式進(jìn)行。
2.2.2 擬合效果衡量指標(biāo)選取 通過最小二乘法擬合得到近似方程后,導(dǎo)入SPSS 25進(jìn)行相關(guān)指標(biāo)計(jì)算。本文選用擬合優(yōu)度(R2)、顯著度(sig)、均方根誤差(root mean square error,RMSE)及平均相對(duì)誤差(mean relative error,MRE)4個(gè)指標(biāo)以衡量擬合的合理性。其中,sig,RMSE是基本合格性指標(biāo),反映擬合方程是否具有基本的可信度。顯著度(sig)方面,通常認(rèn)為其在95%的置信區(qū)間下小于0.05,則具有可信度。RMSE表示擬合結(jié)果總體的離散程度,其值越高代表擬合數(shù)據(jù)越離散,在不同的預(yù)報(bào)區(qū)間偏差較大,易出現(xiàn)較極端的偏差。MRE反映擬合結(jié)果與實(shí)際值偏差大小的百分比,其值越小代表預(yù)測(cè)數(shù)值越逼近實(shí)際數(shù)值,擬合效果越好,是考量近似方程能否逼近真實(shí)數(shù)值的重要指標(biāo),反映擬合方程是否優(yōu)秀。本文將MRE作為衡量擬合效果的主要指標(biāo)。MRE具體計(jì)算方式如式(3)。
(3)
式中:Xn為通過擬合方程所求K預(yù)測(cè)值;XK為由EPIC經(jīng)驗(yàn)公式所求標(biāo)準(zhǔn)K值;n為樣本個(gè)數(shù)(下同)。
2.2.3 平均絕對(duì)偏差多次迭代修正 在求出初步擬合方程的基礎(chǔ)上,若將一定的修正常數(shù)加入原方程對(duì)其進(jìn)行修正,往往能使平均相對(duì)誤差進(jìn)一步下降,但若采用窮舉法“猜”得該常數(shù),往往要耗費(fèi)大量時(shí)間。本文采用多次迭代求取平均絕對(duì)偏差來求出該修正常數(shù)值,對(duì)產(chǎn)生的擬合方程進(jìn)行修正。其原理為通過相減的方式比較預(yù)報(bào)值與實(shí)際值,求得預(yù)報(bào)值與實(shí)際值的偏差大小,并對(duì)所有偏差值之和取平均數(shù)得到平均絕對(duì)偏差值,并重復(fù)迭代運(yùn)行該計(jì)算過程,在MRE最小時(shí)取得理想修正常數(shù),并將其加入原方程,使得擬合方程誤差進(jìn)一步縮小。其計(jì)算方法如下:
(4)
式中:θi為平均絕對(duì)偏差。求出平均絕對(duì)偏差后,將其通過以下途徑修正:
Yi+1(X)=Yi(X)+θi
(5)
式中:Yi+1(X)為本輪修正所得函數(shù);Yi(X)為上輪修正所得函數(shù)。
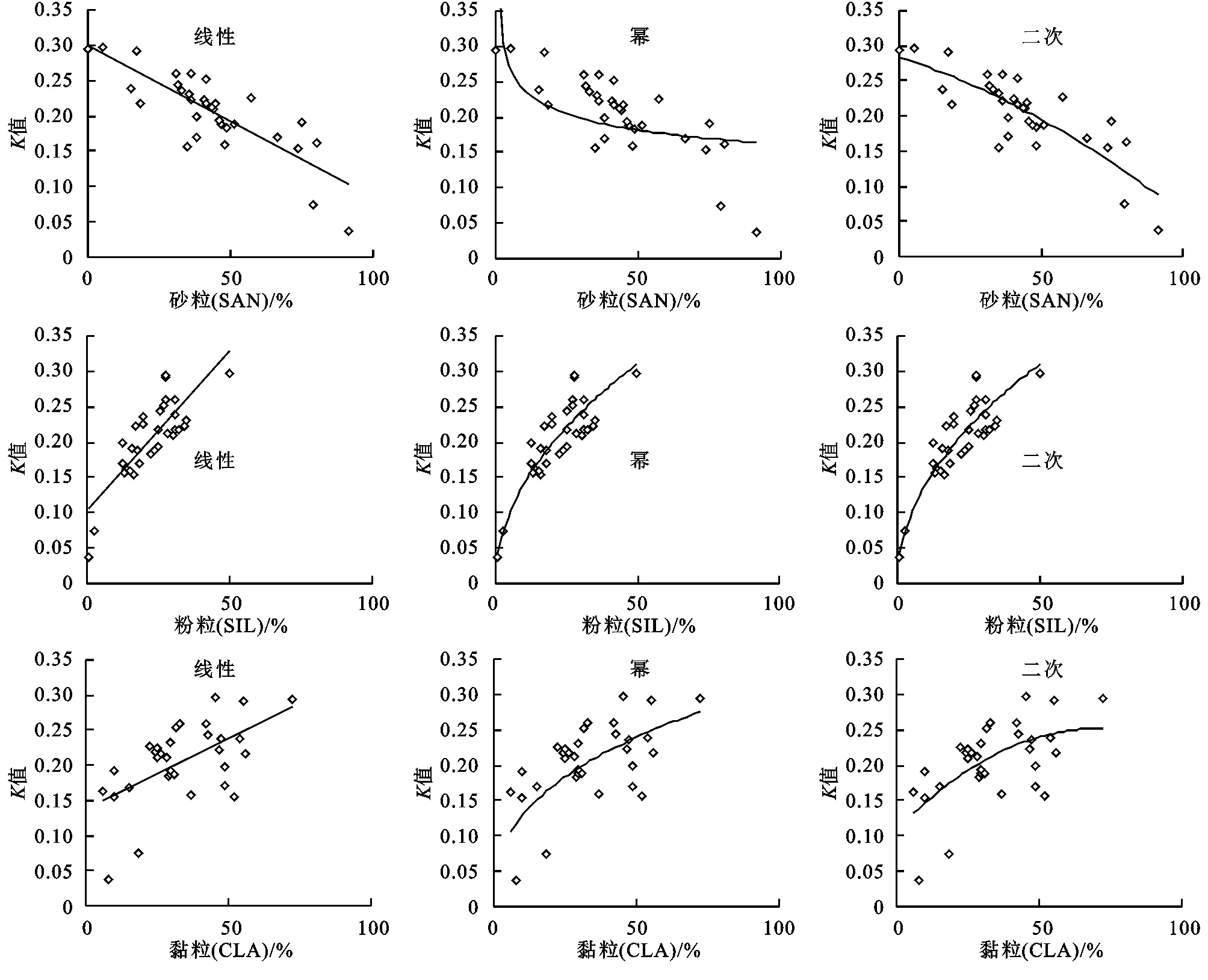
該修正步驟可以重復(fù)迭代進(jìn)行(圖1)。該圖中,MREi代表上一輪迭代的MRE,MREi+1代表本輪迭代的結(jié)果。迭代重復(fù)進(jìn)行至所糾正方程的MRE較上一輪方程更大為止,即若MREi 圖1 平均絕對(duì)偏差多次迭代修正流程示意圖 據(jù)測(cè)量與計(jì)算結(jié)果(表1),茶園紅壤砂粒、粉粒、黏粒含量百分比分別為43.5%,22.8%,33.7%,即茶園紅壤整體上主要以砂粒為主,黏粒次之,粉粒最少,且集中于砂粒與黏粒,質(zhì)地偏向于黏壤土;有機(jī)碳含量平均為2.45%。據(jù)朱鶴健[21]研究,武夷山受人工影響少的自然山地土壤有機(jī)碳含量平均為4.71%,茶園土壤有機(jī)碳含量顯著低于自然山地土壤,這可能與茶園長期耕作導(dǎo)致的有機(jī)質(zhì)流失有關(guān)。 表1 茶園紅壤剖面粒徑平均值及土壤可蝕性K值 對(duì)比M,N層,M層砂粒、粉粒、黏粒3種粒級(jí)平均百分比分別為45.4%,24.0%,30.6%,N層為41.6%,21.7%,36.8%,M層砂粒含量更高,粒徑相對(duì)更大,質(zhì)地偏向于砂質(zhì)黏壤土;N層黏粒含量更高,粒徑相對(duì)小。M層有機(jī)碳含量平均為3.41%,N層為1.38%,差異性顯著(sig<0.05)。有機(jī)質(zhì)更集中于M層,N層有機(jī)質(zhì)相對(duì)較少,其原因可能是N層深度相對(duì)深,日常耕作中施肥的有機(jī)肥類肥料難以深入到達(dá),導(dǎo)致其有機(jī)質(zhì)含量相對(duì)偏低。土壤可蝕性方面,M層K值平均為0.196,N層為0.215,兩者存在明顯差異(sig<0.05)。N層K值較高,發(fā)生水土流失危險(xiǎn)性更大,若M層受降雨等外力侵蝕而被剝離,則暴露的N層由于本身抗侵蝕性較弱,則更易發(fā)生嚴(yán)重的水土流失。 pH值方面,平均pH值M層為4.28,N層為4.62,兩組數(shù)據(jù)存在顯著差異(sig<0.05)。M層土壤相對(duì)N層更酸,pH值更低。其原因是鋁離子為南方紅壤重要的酸性來源,茶本身對(duì)鋁具有特殊的絡(luò)合作用,并以枯枝落葉的形式將鋁離子返還給土壤。N層深度相對(duì)更深,距離表層有一定距離,鋁離子下滲受到的土壤顆粒物阻礙,下滲量較低,到達(dá)N層的鋁離子少,pH值相對(duì)較高,M層由于深度相對(duì)較淺,有較多的鋁離子富集,因此pH值較低。 砂粒(SAN)與K值呈極顯著負(fù)相關(guān)關(guān)系,相關(guān)系數(shù)為-0.819;粉粒(SIL)含量百分比與K值呈極顯著正相關(guān)關(guān)系,相關(guān)系數(shù)達(dá)0.812;砂粒含量與K的相關(guān)性略高于粉粒含量與K的相關(guān)性。黏粒(CLA)含量與K也有極顯著的正相關(guān)性,相關(guān)系數(shù)低于砂粒與砂粒,為0.579。有機(jī)碳(C)與K相關(guān)性不顯著。 表2 不同粒徑土壤含量百分比與土壤可蝕性K值相關(guān)性(R)分析 3.3.1 線性擬合及非線性擬合R2分析 舍棄相關(guān)系數(shù)低的有機(jī)碳數(shù)據(jù),選擇與K值相關(guān)性顯著的砂粒、粉粒與黏粒進(jìn)行曲線擬合。對(duì)3類曲線作函數(shù)圖像(圖2)并求擬合優(yōu)度(R2)(表3)。總體上看,冪函數(shù)在針對(duì)粉粒(SIL)使用時(shí)其擬合優(yōu)度最高,為0.894,顯著優(yōu)于其他8種擬合方程。但在其他兩種變量的擬合中,冪函數(shù)表現(xiàn)相對(duì)不佳。二次多項(xiàng)式在砂粒與黏粒的擬合中表現(xiàn)良好,為相應(yīng)兩種粒級(jí)的最優(yōu)擬合方式,在粉粒擬合中也有較優(yōu)秀的擬合優(yōu)度。 表3 3種函數(shù)擬合方程與擬合優(yōu)度R2分析 圖2 茶園紅壤砂粒、粉粒、黏粒含量百分比與K值擬合結(jié)果 在變量對(duì)比中,粉粒是3種變量中擬合優(yōu)度R2最高的自變量,其平均擬合優(yōu)度為0.764,砂粒的平均R2為0.523,黏粒為0.346,粉粒的擬合優(yōu)度顯著高于砂粒與黏粒。在3種擬合形式中,黏粒的擬合優(yōu)度表現(xiàn)均相對(duì)較差,這可能與其本身相關(guān)性相對(duì)較低有關(guān)。 3.3.2 擬合優(yōu)度與信度分析 進(jìn)一步舍棄擬合優(yōu)度顯著較低的CLA黏粒相關(guān)的擬合方程,將 SAN砂粒、SIL粉粒的3種擬合方程擬合得出的K值與標(biāo)準(zhǔn)K值使用sig,RMSE,MRE進(jìn)行比較(表4)。在顯著度(sig)方面,除SAN一次以外,各個(gè)擬合結(jié)果的顯著度在95%的置信區(qū)間,且顯著性低于0.03,達(dá)到0.02的置信區(qū)間,具有中度顯著性。RMSE中,SAN冪函數(shù)的置信度較差,高于0.05,其余擬合方式置信度在0.03附近波動(dòng),平均值為0.03,總體置信度較為良好,粉粒的擬合結(jié)果在RMSE方面較砂粒更優(yōu)秀。 表4 各函數(shù)擬合效果各指標(biāo)分析 體現(xiàn)數(shù)值逼近程度的MRE(%)方面,各個(gè)方程相差較大。SIL冪函數(shù)是絕對(duì)數(shù)值最逼近的擬合方程,其平均偏差為10.840,較其他擬合方式優(yōu)勢(shì)較為明顯。SAN的3種擬合方式中,二次多項(xiàng)式誤差較小且置信度較高。結(jié)合sig,RMSE,MRE及擬合優(yōu)度R2對(duì)比結(jié)果,在3種不同擬合方式中,對(duì)于不同變量有不同的最優(yōu)擬合方案,對(duì)砂粒而言,二次多項(xiàng)式為最優(yōu)方式,而對(duì)粉粒而言最優(yōu)方式則為冪函數(shù)。且在所有方程中,SIL冪函數(shù)擬合為偏差最小的擬合方程。 綜合上文,最優(yōu)擬合分別在SAN取多項(xiàng)式及SIL取冪函數(shù)時(shí)取得。對(duì)于砂粒(SAN),其最優(yōu)擬合方程為y=-9E-06x2-0.0013x+0.2835;對(duì)于粉粒(SIL),其最優(yōu)擬合方程為y=0.0457x^0.489。但兩種方程仍與K值存在不可忽視的誤差。聯(lián)合兩種擬合方程,先通過SPSS多元線性回歸分析求出各個(gè)方程對(duì)K值影響程度的標(biāo)準(zhǔn)化系數(shù)β,并對(duì)其進(jìn)行歸一化處理得到影響權(quán)重系數(shù),建立初步擬合方程,再進(jìn)一步使用平均絕對(duì)偏差多次迭代修正的方法對(duì)K值進(jìn)行修正。根據(jù)各個(gè)單一變量方程的誤差與置信度表現(xiàn),選擇SIL冪函數(shù)和SAN二次、SIL冪函數(shù)與SIL二次多項(xiàng)式進(jìn)行組合。 以SIL冪函數(shù)結(jié)合SAN二次為例,先將單一變量方程所求K值與實(shí)際K值進(jìn)行多元回歸分析,求得各個(gè)方程對(duì)K值的貢獻(xiàn)率,即標(biāo)準(zhǔn)化系數(shù)β: βSIL冪函數(shù)=0.562βSAN多項(xiàng)式=0.416 (6) 對(duì)其進(jìn)行歸一化處理,將其轉(zhuǎn)化為方程權(quán)重系數(shù): αSIL冪函數(shù)=0.575αSAN多項(xiàng)式=0.425 (7) 得未多次迭代修正原始方程K1: 0.2835)+0.575×(0.0457x20.489) (8) 該方程在迭代五次后得到最優(yōu)修正常數(shù): θK1=-0.0159 (9) 得迭代修正方程: 0.2835)+0.575(0.0457x20.489)-0.0159 (10) 式中:x1為砂粒(SAN)含量百分比(%);x2為粉粒(SIL)含量百分比(%);K為土壤可蝕性因子(下同)。同理,對(duì)SIL冪函數(shù)結(jié)合SIL二次多項(xiàng)式進(jìn)行相同處理,得未修正方程K3;該方程最優(yōu)修正常數(shù)在迭代三次后取得,進(jìn)一步推得擬合方程K4: αSIL冪函數(shù)=0.777αSIL多項(xiàng)式=0.223 (11) 0.777(0.0457x20.489) (12) θK3=-0.0077 (13) 0.777(0.0457x20.489)-0.0077 (14) 各個(gè)方程擬合效果與單一變量方程對(duì)比見表5。各個(gè)方程顯著度sig都較優(yōu)秀。實(shí)際運(yùn)行證明,平均絕對(duì)誤差多次迭代修正具有降低相對(duì)誤差值的能力,但對(duì)于不同的擬合方程,其修正能力差別較大,若在“拐點(diǎn)”前迭代次數(shù)越多,則最終修正值絕對(duì)值越大,修正效果越好,MRE降低的幅度也越高。且在實(shí)際運(yùn)行中發(fā)現(xiàn),若在拐點(diǎn)前迭代的輪數(shù)越高,則得到的單輪修正常數(shù)也越大,也越容易使迭代過程接近或超過拐點(diǎn)。對(duì)于SIL冪函數(shù)結(jié)合SAN二次而言,迭代過程運(yùn)行了5輪,最終求得的修正常數(shù)絕對(duì)值也較大,且將MRE由11.716降為9.673,誤差下降2.043,修正效果明顯;但對(duì)于SIL冪函數(shù)結(jié)合SIL二次而言,其迭代輪數(shù)較低,只運(yùn)行了3輪,修正效果相對(duì)較差,只將MRE由11.064降低為10.606。另外,該修正方法具有加劇數(shù)據(jù)離散程度的副作用,對(duì)于不同方程其加劇程度不同,如對(duì)于K3而言,其將RMSE由0.027提升至0.123,造成了較大的數(shù)值波動(dòng),但對(duì)于K1而言,其副作用又相對(duì)較小,這可能與前期方程組合形式及權(quán)重系數(shù)的不同有關(guān)。 表5 各擬合方程擬合效果對(duì)比 綜合上文,K2的整體誤差下降較多,預(yù)報(bào)精度提升較大,且其MRE值低于最優(yōu)的單因子擬合方程SIL冪函數(shù),較適合作為最終的擬合方程。該方程對(duì)于不同層次的土壤,預(yù)報(bào)精度差異也較大。對(duì)于M層,其MRE值為7.542,對(duì)于N層則為11.805,N層顯著高于M層。對(duì)于M層而言該方程MRE小于10%,預(yù)報(bào)精度相對(duì)優(yōu)秀,所以該方程較適合針對(duì)淺層土壤使用。 結(jié)合實(shí)際運(yùn)用,單因素?cái)M合方程中,SIL冪函數(shù)擬合效果最好,誤差小,但粉粒(SIL)在實(shí)際測(cè)量實(shí)踐中往往是通過扣除砂粒與粉粒的百分比獲得,實(shí)際運(yùn)用較為不便;砂粒(SAN)在實(shí)際測(cè)量中較方便,但其擬合方程誤差較高,預(yù)報(bào)值與實(shí)際值偏離較大,可能可以用于戶外采樣土壤K值的初步比較,單因素方程的運(yùn)用潛力有待商榷。但若測(cè)得兩種粒徑百分比數(shù)據(jù),使用雙因素方程(K2),則可獲得較良好的預(yù)報(bào)效果,此時(shí)該方程的運(yùn)用意義是略去了有機(jī)碳的測(cè)量,為缺乏試驗(yàn)條件的地區(qū)提供一定計(jì)算途徑。 (1)武夷山丘陵茶園紅壤粒級(jí)構(gòu)成以砂粒及黏粒為主,粉粒含量較少,土壤質(zhì)地偏向黏壤土,其中M層砂粒更多,N層黏粒更多,N層有機(jī)質(zhì)較M層更少,N層pH值較M層更高。非耕作層較耕作層更易被侵蝕,應(yīng)尤其注重對(duì)非耕作層的保護(hù)。 (2)該地丘陵茶園紅壤砂粒含量百分比與K值呈極顯著負(fù)相關(guān)關(guān)系,粉粒及黏粒含量百分比與K值呈極顯著正相關(guān)關(guān)系,有機(jī)碳含量與K值相關(guān)性不顯著。 (3)砂粒、粉粒通過線性、冪函數(shù)與二次多項(xiàng)式3種擬合方式,可與K值建立較顯著的擬合方程。綜合評(píng)估3種擬合方式,不同變量條件下最優(yōu)擬合方式不同,二次多項(xiàng)式對(duì)砂粒最優(yōu),冪函數(shù)對(duì)粉粒最優(yōu),且冪函數(shù)擬合效果MRE值顯著較小,能較好貼合K值變化特征。粉粒擬合效果優(yōu)于砂粒,黏粒的擬合效果相對(duì)較差。聯(lián)系兩種方程,通過二元線性回歸計(jì)算賦予權(quán)重系數(shù),并結(jié)合平均絕對(duì)誤差多次迭代修正,可進(jìn)一步降低方程平均相對(duì)誤差,使預(yù)報(bào)值更接近實(shí)際值。同時(shí),本文所求擬合方程對(duì)M層的預(yù)報(bào)精度顯著高于N層,較適合針對(duì)M層土壤使用。 (4)根據(jù)不同單因素?cái)M合方程對(duì)K值的貢獻(xiàn)率,賦予不同的權(quán)重系數(shù),并結(jié)合平均絕對(duì)誤差多次迭代修正,可作為降低擬合方程誤差的一種可能途徑進(jìn)行研究。 本研究受限于可獲取的數(shù)據(jù)量與數(shù)據(jù)代表性,僅針對(duì)武夷山丘陵茶園這一特定地區(qū)提出特定方程擬合的可能可行方法,有一定局限性,擬合方程誤差整體偏大,且對(duì)于平均絕對(duì)誤差多次迭代修正的內(nèi)在機(jī)制并未完全明晰。在后續(xù)研究中,可將從單一因子建立擬合方程求取近似值的思路運(yùn)用至其他地區(qū)以推而廣之,對(duì)平均絕對(duì)誤差多次迭代修正的合理性與可行性及其內(nèi)在機(jī)制進(jìn)行進(jìn)一步驗(yàn)證,并從統(tǒng)計(jì)數(shù)學(xué)角度采取其他方法進(jìn)一步降低方程誤差,以提高擬合精度。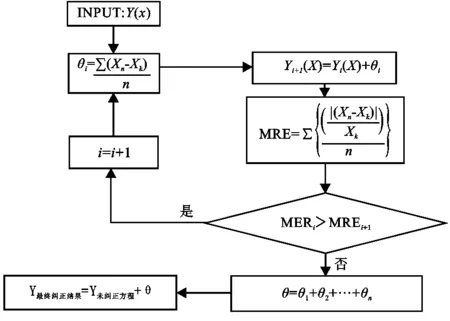
3 結(jié)果與分析
3.1 不同深度土壤總體特征比較
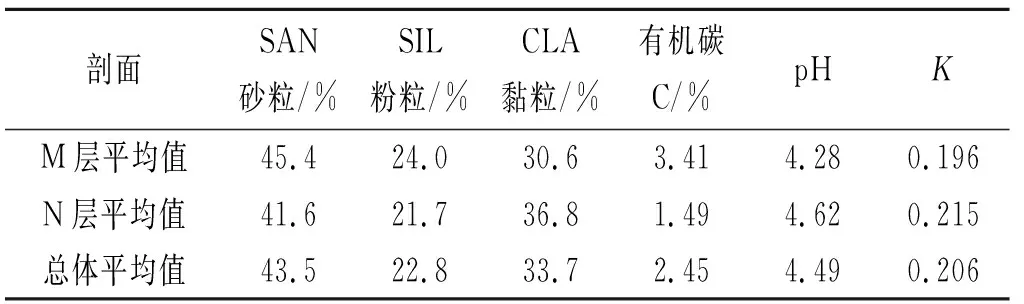
3.2 土壤顆粒粒徑與土壤可蝕性K值相關(guān)關(guān)系比較

3.3 砂粒(SAN)、粉粒(SIL)與K值擬合方程建立


3.4 武夷山茶園紅壤可蝕性近似方程的優(yōu)化
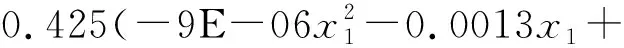
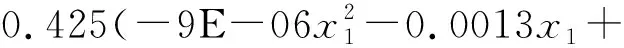



4 結(jié) 論

