具有Robin 邊界條件的時間分?jǐn)?shù)階擴(kuò)散方程的源項辨識問題研究*

崔建譞， 石成鑫， 柳 冕， 程 浩

（江南大學(xué) 理學(xué)院，江蘇 無錫 214122）

引 言

近幾十年來，分?jǐn)?shù)階微分方程被廣泛應(yīng)用在地震波勘探、黏彈性、反常擴(kuò)散、生物材料和混沌動力學(xué)等許多領(lǐng)域，已經(jīng)成為數(shù)學(xué)和物理學(xué)的熱門研究課題之一.相較于整數(shù)階微分方程，分?jǐn)?shù)階微分方程具有記憶和遺傳性質(zhì)，使得其在描述反常擴(kuò)散現(xiàn)象時更有效，因此受到了學(xué)者們的廣泛關(guān)注，而分?jǐn)?shù)階擴(kuò)散方程就是其中一類重要的分?jǐn)?shù)階微分方程.

目前關(guān)于分?jǐn)?shù)階擴(kuò)散方程正問題的研究已經(jīng)相對完善，包括極值原理[1]、解的存在唯一性理論[2]、有限差分法[3-4]、有限元法[5]和譜方法[6]等，但是關(guān)于分?jǐn)?shù)階擴(kuò)散方程反問題的研究結(jié)果還相對較少，源項辨識問題是分?jǐn)?shù)階擴(kuò)散方程反問題的一個重要分支.許多學(xué)者使用不同方法研究了分?jǐn)?shù)階擴(kuò)散方程源項辨識問題：Zhang 等[7]通過解析延拓和Laplace 變換證明解的唯一性，并運(yùn)用Tikhonov 正則化方法進(jìn)行數(shù)值求解；Tuan 等[8]在Dirichlet 邊界條件下考慮了源項辨識問題，得到了精確解與正則近似解之間的先驗誤差估計；Wei 等[9]考慮了一種變系數(shù)的時間分?jǐn)?shù)階擴(kuò)散方程，并用一種修正的擬邊界方法辨識了源項；Yang 等[10]利用Landweber 迭代正則化方法，分別給出了先驗和后驗正則化參數(shù)選擇規(guī)則下的收斂性誤差估計；Wang 等[11]考慮了二維時間分?jǐn)?shù)階擴(kuò)散方程，提出了一種新的數(shù)值方法，給出了正則近似解.上述研究結(jié)果大多考慮的是Dirichlet 或Neumann 邊界條件下的分?jǐn)?shù)階方程的源項辨識問題，然而Robin 邊界條件的物理模型在描述邊界上熱流變化與界面內(nèi)外溫度差之間的關(guān)系上有著廣泛的應(yīng)用背景.因此，本文考慮更為一般的Robin 邊界條件下的時間分?jǐn)?shù)階擴(kuò)散方程：

該源項辨識問題是不適定的，因此需要進(jìn)行正則化處理.我們使用迭代正則化方法解決不適定問題，同時給出先驗和后驗正則化參數(shù)選取規(guī)則，以及正則近似解和精確解之間的誤差估計，并給出了數(shù)值算例.

本文主要結(jié)構(gòu)如下：第1 節(jié)給出了正問題的求解過程并分析了反問題的不適定性；第2 節(jié)介紹了正則化方法，并給出了先驗和后驗參數(shù)選取規(guī)則下的誤差估計；第3 節(jié)通過數(shù)值算例說明了該方法的有效性；最后一節(jié)給出了全文的總結(jié).

1 問題求解與不適定性分析

為了便于計算，將問題（1）中的非齊次邊界條件轉(zhuǎn)化為齊次邊界條件，做如下變換：

2 正則化方法與誤差估計

對于不適定問題的求解，經(jīng)典的方法有Tikhonov 正則化和Landweber 迭代方法[17].本文給出了三種Landweber 迭代型正則化方法求解反問題（2）.首先給出經(jīng)典的Landweber 迭代方法：

2.1 先驗誤差估計

結(jié)合式（8）和（9），并選取m=[(E/δ)2/(p+1)]，證畢.

2.2 后驗誤差估計

在上一小節(jié)中，我們給出了先驗規(guī)則下的正則化參數(shù)m=[(E/δ)2/(p+1)]，但事實上先驗界E是很難獲得的，因此下面我們將考慮不依賴任何先驗信息的后驗參數(shù)選取規(guī)則.

采用偏差原理，正則化參數(shù)m的 選取滿足

其中ω ＞1是一個常數(shù).

定理3 假設(shè)f(x)是 反問題（2）的精確解，fm,δ(x)是由式（5）給出的正則近似解，噪聲估計（6）和先驗界條件（7）成立，正則化參數(shù)m由偏差原理（10）給出，則有以下誤差估計：

結(jié)合式（11）和（12），證畢.

3 數(shù) 值 算 例

在這一節(jié)中，我們將給出數(shù)值算例來驗證迭代型正則化方法的有效性.由于正問題（1）的精確解很難獲得，我們使用有限差分法求解正問題（即假定F(x,t)=r(t)f(x)+Z(x,t)、 初值條件 ?(x)以及Robin 邊界條件μ1(t) 和μ2(t)已 知）來獲得終值數(shù)據(jù)g(x).

在數(shù)值實驗中，空間和時間離散點數(shù)分別為H+1,N+1， 相應(yīng)的步長分別為h=L/H， τ=T/N，并記xi=ih(i=0,1,···,H)，tn=nτ(n=0,1,···,N)， 令uni=u(xi,tn)，F(xiàn)in=F(xi,tn)為網(wǎng)格點處的值.

正問題（1）中的時間項導(dǎo)數(shù)可以通過Caputo 分?jǐn)?shù)階導(dǎo)數(shù)的L1插值逼近[19]來近似得到：

圖1 ～ 3 中圖（a）采用先驗參數(shù)選取規(guī)則計算正則近似解；圖1 ～ 3 中圖（b）采用后驗參數(shù)選取規(guī)則計算正則近似解.表1～3 給出了在不同誤差水平下精確解和正則近似解的絕對誤差和相對誤差.

從圖1 ～ 3 可以看出，先驗和后驗正則化參數(shù)選取規(guī)則下計算的源項正則近似解與精確解之間的逼近效果都較好，而且當(dāng)解的光滑性變好時，數(shù)值結(jié)果也會變好.從表1 ～ 3 可以看出，隨著 ε的增大，絕對誤差和相對誤差都會增大，這與理論結(jié)果相符合.還可以看出，后驗正則化參數(shù)選取規(guī)則下的數(shù)值結(jié)果幾乎可以媲美先驗正則化參數(shù)選取規(guī)則下的數(shù)值結(jié)果，這說明了本文的方法是有效的.

表1 算例1 在不同誤差水平下的絕對誤差和相對誤差Table 1 Absolute errors and relative errors under different error levels of example 1

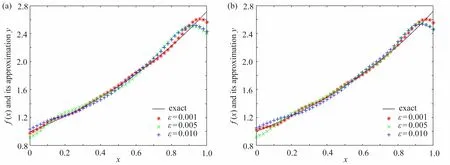
圖1 算例1 的精確解及其正則近似解：(a)先驗規(guī)則；(b)后驗規(guī)則Fig. 1 The exact solution and its regularized approximate solution of example 1: (a) the priori rule; (b) the posteriori rule

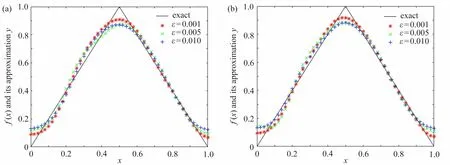
圖2 算例2 的精確解及其正則近似解：(a)先驗規(guī)則；(b)后驗規(guī)則Fig. 2 The exact solution and its regularized approximate solution of example 2: (a) the priori rule; (b) the posteriori rule

圖3 算例3 的精確解及其正則近似解：(a)先驗規(guī)則；(b)后驗規(guī)則Fig. 3 The exact solution and its regularized approximate solution of example 3: (a) the priori rule; (b) the posteriori rule

表2 算例2 在不同誤差水平下的絕對誤差和相對誤差Table 2 Absolute errors and relative errors under different error levels of example 2

表3 算例3 在不同誤差水平下的絕對誤差和相對誤差Table 3 Absolute errors and relative errors under different error levels of example 3

4 結(jié) 論

本文考慮了Robin 邊界條件下的時間分?jǐn)?shù)階擴(kuò)散方程源項辨識問題，給出了三種Landweber 型正則化方法，以TSVD 正則化與分?jǐn)?shù)階Landweber 迭代方法相結(jié)合的方法為例，給出了正則近似解和精確解在不同參數(shù)選取規(guī)則下的誤差估計，數(shù)值部分驗證了方法的有效性.此外該方法還可以推廣到其他反問題，如多項分?jǐn)?shù)階反問題和高維方程反問題等，還有待于進(jìn)一步研究.

參考文獻(xiàn)（ References ） ：

［1］LUCHKO Y. Maximum principle and its application for the time-fractional diffusion equations[J].Fractional Calculus and Applied Analysis, 2011, 14（1）: 110-124.

［2］YAMAMOTO M. Weak solutions to non-homogeneous boundary value problems for time-fractional diffusion equations[J].Journal of Mathematical Analysis and Applications, 2018, 460（1）: 365-381.

［3］LANGLANDS T A M, HENRY B I. The accuracy and stability of an implicit solution method for the fractional diffusion equation[J].Journal of Computational Physics, 2005, 205（2）: 719-736.

［4］ZHUANG P, LIU F. Implicit difference approximation for the time fractional diffusion equation[J].Journal of Applied Mathematics and Computing, 2006, 22（3）: 87-99.

［5］DENG W H. Finite element method for the space and time fractional Fokker-Planck equation[J].SIAM Journal on Numerical Analysis, 2009, 47（1）: 204-226.

［6］SONG F Y, XU C J. Spectral direction splitting methods for two-dimensional space fractional diffusion equations[J].Journal of Computational Physics, 2015, 299: 196-214.

［7］ZHANG Y, XU X. Inverse source problem for a fractional diffusion equation[J].Inverse Problems, 2011, 27（3）:035010.

［8］TUAN N H, LONG L D, THINH N V. Regularized solution of an inverse source problem for a time fractional diffusion equation[J].Applied Mathematical Modelling, 2016, 40（19/20）: 8244-8264.

［9］WEI T, WANG J G. A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation[J].Applied Numerical Mathematics, 2014, 78: 95-111.

［10］YANG F, LIU X, LI X X, et al. Landweber iterative regularization method for identifying the unknown source of the time-fractional diffusion equation[J].Advances in Difference Equations, 2017, 2017: 388-403.

［11］WANG W, YAMAMOTO M, HAN B. Numerical method in reproducing kernel space for an inverse source problem for the fractional diffusion equation[J].Inverse Problems, 2013, 29（9）: 095009.

［12］PODLUBNY I.Fractional Differential Equations[M]. San Diego: Academic Press, 1999.

［13］ 顧樵. 數(shù)學(xué)物理方法[M]. 北京: 科學(xué)出版社, 2012. （GU Qiao.Mathematical Methods for Physics[M]. Beijing: Science Press, 2012. （in Chinese））

［14］MA Y K, PRAKASH P, DEIVEEGAN A. Generalized Tikhonov methods for an inverse source problem of the time-fractional diffusion equation[J].Chaos,Solitons & Fractals, 2018, 108: 39-48.

［15］KLANN E, RAMLAU R. Regularization by fractional filter methods and data smoothing[J].Inverse Problems,2008, 24（2）: 025018.

［16］DENG Y, LIU Z. Iteration methods on sideways parabolic equations[J].Inverse Problem, 2009, 25（9）: 095004.

［17］KIRSCH A.An Introduction to the Mathematical Theory of Inverse Problem[M]. New York: Springer, 1996.

［18］ 于寧. 求解時間分?jǐn)?shù)階擴(kuò)散方程反源問題的分?jǐn)?shù)階Landweber正則化方法[D]. 碩士學(xué)位論文. 濟(jì)南: 山東大學(xué), 2020.（YU Ning. The fractional Landweber regularization method for solving inverse source problem of time-fractional diffusion equation[D]. Master Thesis. Jinan: Shandong University, 2020. （in Chinese））

［19］ 孫志忠, 高廣花. 分?jǐn)?shù)階微分方程的有限差分方法[M]. 北京: 科學(xué)出版社, 2015. （SUN Zhizhong, GAO Guanghua.Finite Difference Method for Fractional Differential Equation[M]. Beijing: Science Press, 2015. （in Chinese））