基于準ARX 模型和SVR 算法的非線性系統切換控制*

王 蘭， 董宜平， 曹進德

（1. 無錫職業技術學院 基礎課部，江蘇 無錫 214121；2. 中科芯集成電路有限公司，江蘇 無錫 214063；3. 東南大學 數學學院，南京 211189）

引 言

非線性系統的自適應控制問題一直是控制領域的研究重點. 部分研究者基于局部線性化的思想，即將非線性系統分解為線性系統，提出了非線性系統的自適應控制方法[1-5]. 然而，局部線性化的方法并不能很好地表達系統的非線性特性，因此該模型面臨著精確性問題. 近年來，機器學習網絡由于其可以無限逼近于非線性函數而吸引了越來越多的研究者關注[6-12]. 非參數化和參數化模型的界限一直比較模糊，機器學習的方法弱化了模型類型的區別，并作為一種基于輸入輸出數據的一般性學習算法在建模及參數估計方面得到了研究和發展，例如基于核函數的辨識方法[8]、基于神經網絡的辨識方法[7,12]、基于模糊邏輯[1,5]的辨識方法等. 然而，在設計和使用該類控制系統的過程中，必須充分考慮參數辨識、控制律推導以及控制系統穩定性和魯棒性等問題.

為了解決這些問題，一種特殊的模塊化模型：含有外部輸入項的準線性自回歸(autoregressive with eXogenous inputs, ARX) 模型被提出. 文獻[1]對該模型的建立和特點進行了詳細說明. 近年來，該模型已成功應用于非線性系統的控制器設計、真實系統的辨識與控制、時序預測等領域[5,8,13]. 準ARX 模型通過模型的多模塊來實現不同功能并表達系統特性，主要優勢在于將模型線性和非線性分離于不同模塊中，從而使得模型穩定性可通過線性部分來確保. 因為可以通過切換機制提高線性控制的精度，同時又可以給非線性控制提供穩定性保障，所以控制切換的思想在很多文獻中被采用[11,14-15]. 文獻[11]提出了一種包含切換機制的準ARX 網絡模型，基于模型的線性部分和非線性部分的預測誤差，建立了切換判定函數. 基于該模型的切換控制系統既可以保障控制的精度，又可以解決穩定性問題.

然而，該控制系統仍然面臨三個挑戰：基于神經網絡的準ARX 模型的參數并沒有充分利用先驗知識，其參數沒有可用的解釋；當系統具有較大的擾動時，原有的控制器設計方法并不具有很好的魯棒性；切換機制引入預測系統，基于預測模型設計的控制器還是多個.

基于上述討論，本文采用徑向基函數(radial basis function, RBF) 網絡代替準線性ARX 模型中非線性部分的神經網絡.RBF 網絡具有簡單的拓撲結構和計算精度高等優點，被廣泛用于非線性系統控制.同時，采用近鄰傳播聚類(affinity propagation, AP)聚類方法生成系統的數據分布信息，每個RBF 網絡的參數根據距離其他中心的距離來設置，從而為準ARX 模型提供一種可解釋的辨識方法.引入切換機制，設計一個基于線性部分和非線性部分誤差的切換控制器，給出穩定性說明.支持向量回歸(support vector regression, SVR)在模式識別和函數估計中可以確保參數的穩健性，尤其是控制對象存在很大的擾動時[16-17].為了提高控制系統的魯棒性，利用一個線性SVR 算法取代最小二乘算法算法.

本文的結構如下：第1 節進行了問題的描述；第2 節提出了一種改進的準ARX 切換模型；第3 節給出了模型參數辨識方法；第4 節基于預測模型設計了系統的控制器，并分析了其穩定性，同時通過仿真例子說明了模型的有效性；第5 節給出了全文的總結.

1 問 題 描 述

本文研究如下單輸入單輸出(SISO)非線性時不變系統[18]，其輸入輸出關系記作

其中 φ (t)=[y(t-1) ···y(t-n)u(t-d) ···u(t-m-d+1)]T,u(t)∈R,y(t)∈R，v(t)∈R 分別是t時刻系統的輸入、輸出以及零均值的隨機噪聲；m和n分別為未知的輸入、輸出最大時滯，d為已知的整數時延； φ(t)∈Rs，s=n+m是對應的回歸變量；g(·) 是非線性函數.給出如下假設[1]：

假設1 (ⅰ)g(·) 是一個連續函數, 在 φ (t)=0 處是C∞連續；(ⅱ) 系統具有全局一致漸近穩定的零動態特性；(ⅲ) 系統是可控的，且存在一個控制器可以表示為：u(t)=ρ(ξ(t)), 其中ξ(t)=[y(t) ···y(t-n)u(t-1) ···u(t-m)y*(t+1) ···y*(t+1-l)]T(y*(t) 表示參考輸出).

2 改進的準 ARX 預測模型

2.1 回歸表示

在假設條件下，系統(1)的函數g(·)在 φ (t)=0 鄰域內進行Taylor 展開，可以得到

2.2 d-步預測器

基于文獻[1]中的推導方法，得到預測器的表達式為

2.3 基于RBF 的準ARX 模型

其中 Ωj={λj,Zj} 是RBF 網絡的參數集；Zj為網絡的中心； λj表示基函數的寬度參數；算子 ‖ ·‖2表示向量的2 范數；M代表基函數的個數； ξ (t),χ(t) 是RBF 網絡的輸入項，在前面已經定義.

3 模型參數辨識

模型 (11)的參數分為兩類：線性部分參數 Θ 以及非線性部分參數 ? ,Ωj.分別采用不同的參數辨識方法進行.

3.1 線性部分參數

3.2 非線性部分參數

3.2.1 聚類方法

中心參數的選擇對RBF 型網絡的性能起著重要的作用.本文中，該部分參數是通過聚類方法利用先驗知識得到而不是通過最小化訓練誤差的均方來估計的.需要指出的是，在RBF 網絡中使用聚類方法來初始化中心參數并不是一個新的思路，而本文采用的參數辨識方法，具有有意義的解釋[8].

通過聚類算法生成數據的局部線性信息，其中簇的數目（線性子空間）等于RBF 基函數的數目M，并且每個聚類中心被設置為相關RBF 的中心參數Zj.為了適當地確定每個局部線性子模型的操作區域，設置每個RBF 的寬度 λj以很好地覆蓋相應的子空間.本文采用系數 ρ 乘以訓練數據之間最大距離.

3.2.2 支持向量回歸方法

該優化問題可以變換為尋找相關Lagrange 函數的鞍點問題：

3.3 切換律

4 控 制 仿 真

4.1 控制器設計

該部分非線性系統的控制器設計包含兩個步驟：第一步辨識改進的準ARX 預測模型；第二步控制序列的推導和實施.通過前面的推導，我們可以得到被辨識的預測模型為

基于文獻[19]的方法，分析可得非線性系統(3)的自適應控制器(23)的穩定性：輸入輸出信號在閉環系統內是有界的.此外，當選取合適的徑向基函數網絡時，系統的跟蹤誤差收斂于0.

4.2 仿真例子

考慮非線性系統表達式如下：

其中噪聲函數v(t) 為v(t)=(1+0.3q-1)e(t),e(t)∈N(0,0.02) 為白噪聲.

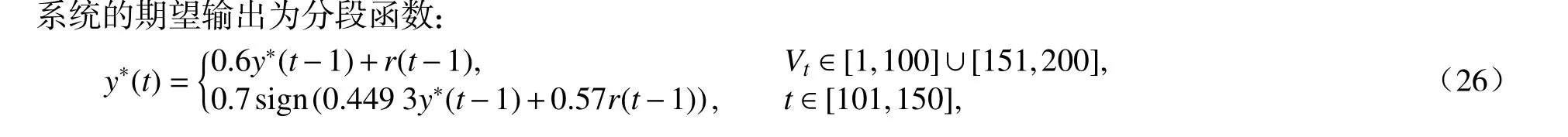
其中r(t)=sin(2πt/25).

基于該例子的仿真，將本節提供的切換控制方法，與線性控制方法(linear control)、基于神經網絡的控制方法(NN control)[19]以及非切換自適應控制方法(third control)進行比較. 非線性部分的徑向基函數網絡參數選為M=6, ρ=0.2， 參數 Ωj則利用聚類算法進行離線訓練得到. 利用線性SVR 算法每10 步計算一次參數?. 切換判別函數中的參數選為c=2.4，N=3.

圖 1 給出了控制結果的展示. 其中，圖1(a) 給出了控制輸出，實線為控制輸出y(t)， 虛線為期望輸出y*(t)；圖1(b) 給出了控制輸入u(t)； 圖1(c)中為切換序列 χ(t). 顯而易見，所提供的控制方法可以很好地在任意時刻實現對期望輸出的追蹤.

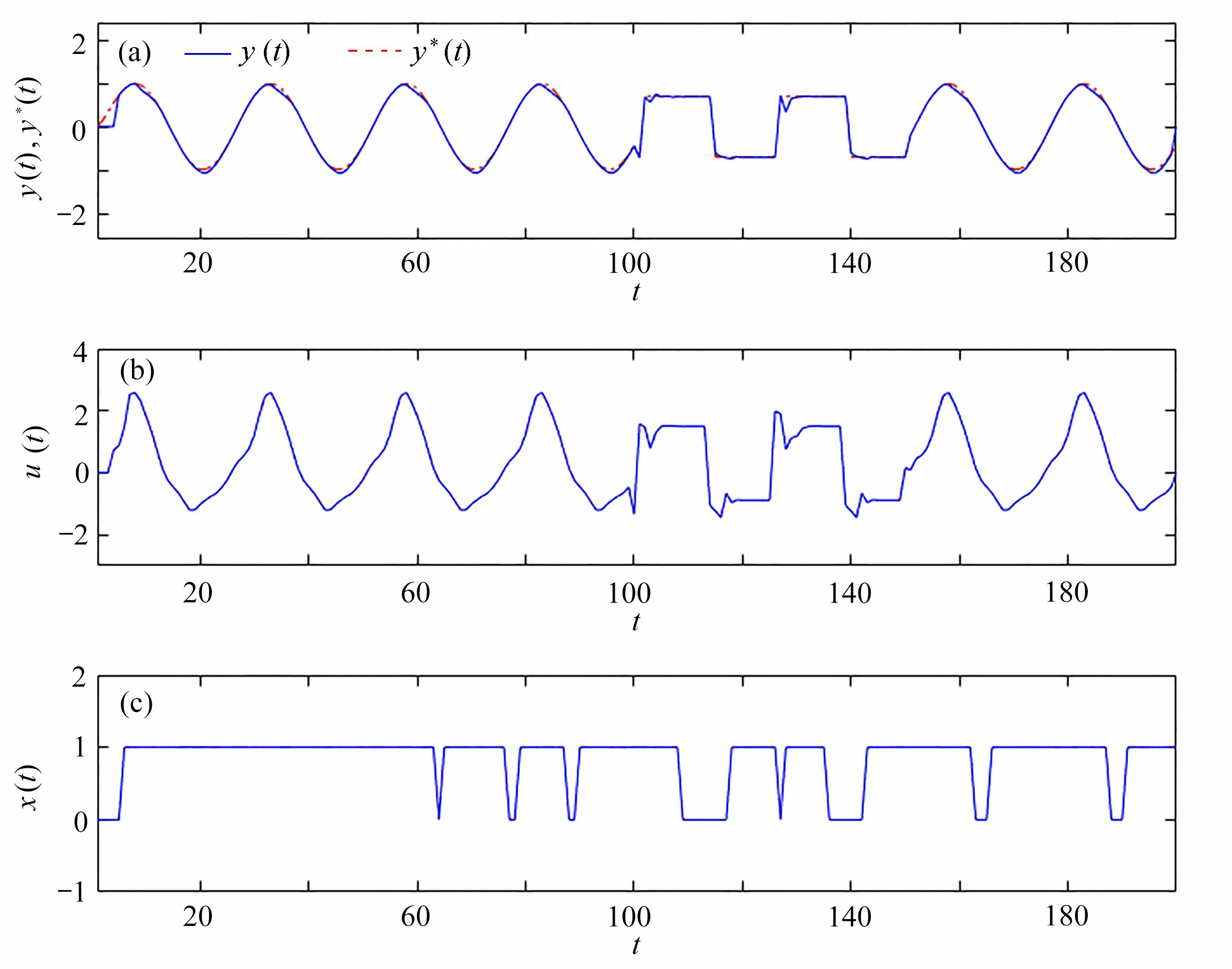
圖1 仿真例子的控制結果圖：(a) 控制輸出 y (t)， 期望輸出 y *(t) ；(b) 輸入序列 u (t) ；(c)切換序列χ(t)Fig. 1 Control results of the example: (a) control output y (t) and desired output y *(t) ; (b) control input u (t) ; (c) switching sequenceχ(t)

表 1 給出了4 種控制方法誤差的均值和方差數據，通過對比可以看出，本文所研究的切換自適應控制在噪聲較大情況下，效果比其他方法控制效果更好.

表1 基于噪聲v (t)情 況下控制誤差對比表v(t)Table 1 Comparison of errors with the noise

5 總 結

本文提出了一種基于改進的準ARX RBF 預測模型的新型非線性系統自適應切換控制器. 一方面，采用聚類方法來揭示預測模型非線性部分的局部線性信息. 雖然在RBF 網絡的參數估計中出現了類似的方法，但對于準ARX 模型的非線性參數給出了有意義的解釋. 另一方面，將SVR 用于模型的線性參數估計. 與基于神經網絡的控制系統不同的是，所提出的控制模型，參數可以通過先驗知識確定，并且對于較大的擾動具有魯棒性. 最后，通過仿真體現所提供的控制方法的有效性.

參考文獻（ References ） ：

［1］H U J, HIRASAWA K, KUMAMARU K. A neurofuzzy-based adaptive predictor for control of nonlinear systems[J].Transactions of the Society of Instrument and Control Engineers, 1999, 35（8）: 1060-1068.

［2］ 趙 瑋, 任鳳麗. 基于自適應控制的四元數時滯神經網絡的有限時間同步[J]. 應用數學和力學, 2022, 43（1）: 94-103.（ZHAO Wei, REN Fengli. Finite time adaptive synchronization of quaternion-value neural networks with time delays[J].Applied Mathematics and Mechanics, 2022, 43（1）: 94-103.（in Chinese））

［3］Y OUNG P C, MCKENNA P, BRUUN J. Identification of non-linear stochastic systems by state dependent parameter estimation[J].International Journal of Control, 2001, 74（18）: 1837-1857.

［4］X I Y G, LI D W, LIN S. Model predictive control-status and challenges[J].Acta Automatica Sinica, 2013, 39（3）:222-236.

［5］ 王 蘭, 謝達, 董宜平, 等. 基于準 ARX 多層學習網絡模型的非線性系統自適應控制[J]. 應用數學和力學, 2019,40（11）: 1214-1223. （WANG Lan, XIE Da, DONG Yiping, et al. Adaptive control of nonlinear systems based on quasi-ARX multilayer learning network models[J].Applied Mathematics and Mechanics, 2019, 40（11）: 1214-1223.（in Chinese））

［6］N ARENDRA K S, PARTHASARATHY K. Identification and control of dynamical systems using neural networks[J].IEEE Transactions on Neural Networks, 1990, 1（1）: 4-27.

［7］L I D P, LIU Y J, TONG S C, et al. Neural networks-based adaptive control for nonlinear state constrained systems with input delay[J].IEEE Transactions on Cybernetics, 2019, 49（4）: 1249-1258.

［8］W ANG L, CHENG Y, HU J, et al. Nonlinear system identification using quasi-ARX RBFN models with a parameter-classified scheme[J].Complexity, 2017, 2017: 1-12.

［9］W U J, SUN W, SU S F, et al. Neural-based adaptive control for nonlinear systems with quantized input and the output constraint[J].Applied Mathematics and Computation, 2022, 413: 126637.

［10］B ILLINGS S A, WEI H L. A new class of wavelet networks for nonlinear system identification[J].IEEE Transactions on Neural Networks, 2005, 16（4）: 862-874.

［11］W ANG L, CHENG Y, HU J. Stabilizing switching control for nonlinear system based on quasi-ARX RBFN model[J].IEEJ Transactions on Electrical and Electronic Engineering, 2012, 7（4）: 390-396.

［12］C HENG L, WANG Z, JIANG F, et al. Adaptive neural network control of nonlinear systems with unknown dynamics[J].Advances in Space Research, 2021, 67（3）: 1114-1123.

［13］J ANOT A, YOUNG P C, GAUTIER M. Identification and control of electro-mechanical systems using state-dependent parameter estimation[J].International Journal of Control, 2017, 90（4）: 643-660.

［14］Y ANG D, LI X, QIU J. Output tracking control of delayed switched systems via state-dependent switching and dynamic output feedback[J].Nonlinear Analysis: Hybrid Systems, 2019, 32: 294-305.

［15］B ECHLIOULIS C P, ROVITHAKIS G A. Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems[J].IEEE Transactions on Automatic Control, 2010, 55（5）: 1220-1226.

［16］A WAD M, KHANNA R.Support Vector Regression[M]//Efficient Learning Machines.Berkeley: Apress, 2015:67-80.

［17］T OIVONEN H T, T?TTERMAN S, ?KESSON B M. Identification of state-dependent parameter models with support vector regression[J].International Journal of Control, 2007, 80（9）: 1454-1470.

［18］G OOGWIN G C, SIN K S.Adaptive Filtering Prediction and Control[M]. Dover Publications, 1984.

［19］W ANG L, CHENG Y, HU J. A quasi-ARX neural network with switching mechanism to adaptive control of nonlinear systems[J].SICE Journal of Control, Measurement, and System Integration, 2010, 3（4）: 246-252.