相變材料耦合冷板電池熱管理系統的優化設計*

黃 欽， 余凌峰， 陳 凱

（華南理工大學 化學與化工學院 傳熱強化與過程節能教育部重點實驗室，廣州 510640）

引 言

隨著全球經濟高速發展，能源危機和環境污染問題日益突出，各國都在倡導綠色環保的低碳交通方式，電動汽車得以蓬勃發展.動力電池作為電動汽車三大組件之一，是電動汽車的驅動核心.電動汽車動力性能和續航里程的提升，對電池比容量、高倍率充放電提出了更高的要求，電池充放電過程是一個產熱過程，若產生的熱量無法及時散出，將引起電池溫度上升，導致熱失控[1].因此需要對動力電池進行熱管理，保證其在合適的溫度范圍內工作，以維持電動汽車安全穩定運行.

目前，電池熱管理技術有空氣冷卻[2]、液體冷卻[3]、相變材料（PCM）冷卻[4]、熱管冷卻[5]以及不同方式的耦合冷卻[6-8].其中，基于相變材料和冷板的耦合冷卻方式，可以綜合液冷換熱系數高與相變材料均溫性好的優點，實現電池組最高溫度的降低和溫差的減小，是一種非常有應用前景的復合熱管理方式.學者們對相變材料耦合冷板（PCM-LC）熱管理系統的性能開展了大量研究.喻寰[9]研究了系統的運行參數及復合相變材料成分配比對系統冷卻性能的影響，結果表明冷卻液入口流速為0.15 m/s，膨脹石墨質量分數為20%復合相變材料組成的系統能夠達到較好的熱管理效果；Cao 等[10]通過實驗發現液冷進水溫度接近環境溫度可以獲得較優的熱管理性能，在相變材料總質量不變的情況下，相變材料潛熱值比導熱系數的影響更大；Liu 等[11]通過調節運行參數對電池組冷卻模塊進行控溫，結果表明當電池組的冷卻要求不高時，改變進水流量比改變進水溫度更節能；Bai 等[12]研究發現液冷板越靠近電極區域，對電池降溫效果越顯著，而相鄰電池間距增加可以提高系統溫度的均勻性，但對電池最高溫度影響不大；Zhu 等[13]通過對系統運行參數和結構參數進行單因素分析，發現結構參數是影響系統性能的關鍵參數.

為了進一步提高系統性能，學者們對耦合熱管理系統的結構進行優化設計.Li 等[14]研究了系統單側液冷板與雙側液冷板的冷卻性能，結果表明雙側液冷板可顯著降低電池組溫差，并使電池在4 C 高倍率放電結束后最高溫度低于50 ℃.Wang 等[15]也比較了單側與雙側液冷板情況下的系統性能，發現雙側液冷板使5 C 倍率放電結束后的電池組最高溫度從64 ℃降低到46.3 ℃.Molaeimanesh 等[16]在保證系統體積不變的情況下，改變相變材料與多個液冷板的布局方式對電池模塊進行冷卻，降低了電池組的最高溫度并改善了其溫度均勻性；Cao 等[17]優化了相變材料耦合液冷系統中冷板的內流道布置，結果表明增大流道間距并將相鄰流道內的液體反向流動可以有效減少電池組的徑向溫差.

現有研究表明，相變材料耦合冷板系統的結構顯著影響系統的冷卻性能.而對于耦合系統結構的優化方法，主要通過枚舉設計不同系統結構進行模擬實驗，分析各自的溫度特性從而局部尋優，帶入的經驗性阻礙了系統性能的進一步提高.針對上述問題，本文以相變材料耦合冷板系統為研究對象，采用數值方法研究進口工質流量對系統冷卻性能的影響規律.隨后，采用優化策略對耦合系統中相變材料的厚度分布進行優化設計，在保證系統體積不變的情況下，降低電池組最高溫度并改善其溫度均勻性.

1 數 值 模 型

1.1 物理模型

圖1 為本文研究的相變材料耦合冷板電池熱管理系統.其中，系統中的電池組包含8 × 2 個方形電池，液冷板分別與電池兩個側面緊密貼合，沿著液冷板內并行流道方向上，相鄰電池之間填充相變材料.其中相鄰電池的相變材料厚度為4 mm，冷板進口和出口附近相變材料厚度為2 mm.引入文獻[18-19]中的電池和石蠟/EG 復合相變材料，其中電池尺寸為18 mm × 65 mm × 90 mm.采用文獻[20]中的微通道冷板，其尺寸為176 mm ×130 mm × 2 mm，進、出口長度為65 mm，冷板內流道的厚度為0.6 mm，內部包含五條并行流道，流道寬度為12 mm.冷板的材質為鋁，冷卻工質為水，鋁、水、相變材料和電池的物性參數如表1 所示.

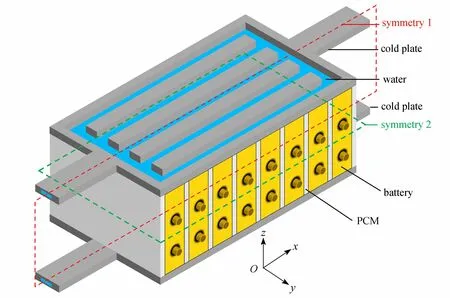
圖1 相變材料耦合冷板系統示意圖Fig. 1 Schematic diagram of the PCM coupled cold plate system

表1 系統中各種材料物性參數Table 1 Physical property parameters of various materials in the system

1.2 控制方程

本文建立了耦合電池熱管理系統的三維數值模型，采用數值方法計算系統的速度場和溫度場.計算過程中假設相變材料不受重力作用，在熔化過程只有熱傳導，無自然流動；忽略各材料之間的接觸熱阻；系統中各物性參數視為常數，速度場和溫度場計算可以解耦.電池組在放電過程為非穩態產熱過程，采用瞬態能量方程進行模擬；相變材料經歷融化凝固過程，使用焓法進行模擬；冷板中工質采用計算流體力學方法[21]進行模擬.因此，系統各部分的控制方程如下：

電池

其中，I為電池放電電流，Rb為 5 C 放電倍率過程中電池單體的等效電阻，Vb是電池體積，du/dT是電化學量熱法得到電壓溫度系數，值為-0.22 mV/K[22].

相變材料

其中，cp,p是相變材料的比熱容，β表示相變材料的液相率，γ 為相變材料的相變焓，T0表示初始溫度，Ts為固相點溫度，Tl為液相點溫度.

水

其中，ρw為水的密度，ui和uj為Reynolds 平均速度分量，P是Reynolds 平均壓力，ηw為水的動力黏度，cp,w為水的比熱容，λw為水的熱導率，Tw為水的溫度.

冷板

其中，ρc為冷板的密度，cp,c為冷板的比熱容，λc為冷板的熱導率，Tc為冷板的溫度.

1.3 邊界條件及網格無關性驗證

為了求解控制方程，采用以下邊界條件：冷卻水進口邊界設置為質量流量進口，進口溫度和環境溫度為恒定溫度，出口設置為壓力出口；由于忽略了各材料之間的接觸熱阻，不同材料接觸界面設置為溫度連續的無滑移邊界；系統為對稱結構，因此取系統四分之一區域作為計算域，對稱面1 和對稱面2（圖1 所示）均設置為對稱邊界，其余表面均設置為無滑移絕熱邊界.控制方程和邊界條件通過有限體積法離散化[23]，方程中的擴散項由中心差分法離散化.

系統采用結構化網格進行離散，在流固接觸壁面上加密網格保證流動邊界層的計算精度.為了確定合適的網格數，進行了網格無關性驗證.結果表明，當網格數量大于1.5 × 106時，電池組最高溫度和溫差的變化幅度均小于0.1 K.因此，下面將采用類似的網格尺寸對系統進行離散.

2 耦合系統熱管理性能

采用第1 節的數值方法計算相變材料耦合液冷板系統的速度場和溫度場.進口冷卻水流量設置為5 g/s，進口溫度和環境溫度設置為303.15 K.圖2(a)給出了放電結束后系統對稱面1 的溫度云圖.可以看到，電池產生的熱量一部分被周圍的相變材料吸收，一部分被冷板中的冷卻水帶走.冷板中冷卻水在往下游流動過程中不斷吸收電池產熱，溫度逐漸升高.上游冷卻水溫度較低，附近電池產熱更多通過冷卻水帶走；下游冷卻水溫度較高，下游電池更多熱量通過相變材料吸收.圖2(b)給出了放電結束后系統對稱面1 的液相分數（相變率）云圖；可以看到，沿冷卻水流動方向，相變材料的熔化率逐漸升高，下游靠近電池中部附近的相變材料基本熔化，最終導致下游電池溫度較高.因此，沿冷卻水流動方向電池的平均溫度呈現上升趨勢.放電結束后，電池最高溫度Tmax為322.5 K，電池組間溫差ΔT為4.9 K.進一步，考慮不同的進口冷卻水流量m0（5 g/s, 6 g/s, 7 g/s，8 g/s），計算結果如圖3 所示.可以看到，隨著冷卻水流量增加，電池組Tmax和ΔT均減小，但是液冷板系統功耗Wp顯著增加.因此，通過增加冷板進口流量難以有效地提高相變材料耦合冷板系統的冷卻性能.

圖2 放電結束時對稱面1 的計算結果：(a)溫度云圖；(b)相變率云圖Fig. 2 Numerical results of symmetry 1 when the discharge process is finished: (a) the temperature nephogram; (b) the liquid fraction nephogram

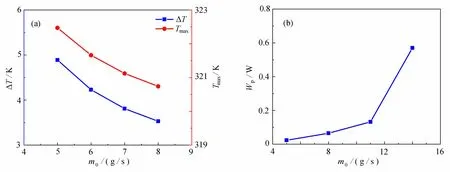
圖3 系統性能指標隨冷卻水流量的變化關系：(a) 電池組Tmax 和ΔT；(b) 系統功耗Fig. 3 System performance with the flow rate of cooling water: (a) Tmax and ΔT of the battery pack; (b) power consumption of the system

3 耦合系統優化設計

在耦合系統中，冷卻液流經并行流道帶走電池產生的熱量，其溫度沿流向逐漸升高，從而造成上下游電池的溫度差異，最終導致靠近冷板進口的上游相變材料熔化速率較慢，利用率較低；靠近冷板出口的下游相變材料熔化速率快，利用率較高.長時間放電后，因相變材料相變率差異而導致電池組出現較大溫差.在已有研究中，Chen 等[19]針對相變材料耦合熱管冷卻系統，采用調整策略改變相變材料的厚度分布，從而調控不同位置相變材料的熔化速率，達到了改善熱管理系統冷卻性能的目標.本文采用類似的思想，引入文獻中的優化策略調整系統中相變材料的厚度分布，調控不同位置相變材料的利用效率，從而降低電池組溫差.圖4 給出了耦合系統的主視圖.為了方便識別調整區域位置，將相變材料的厚度分布記為L=[L1，L2，···，Li，···，LN，LN+1]，其中，N為電池個數，Li為第i個相變材料的厚度.采用以下優化策略對L進行優化：

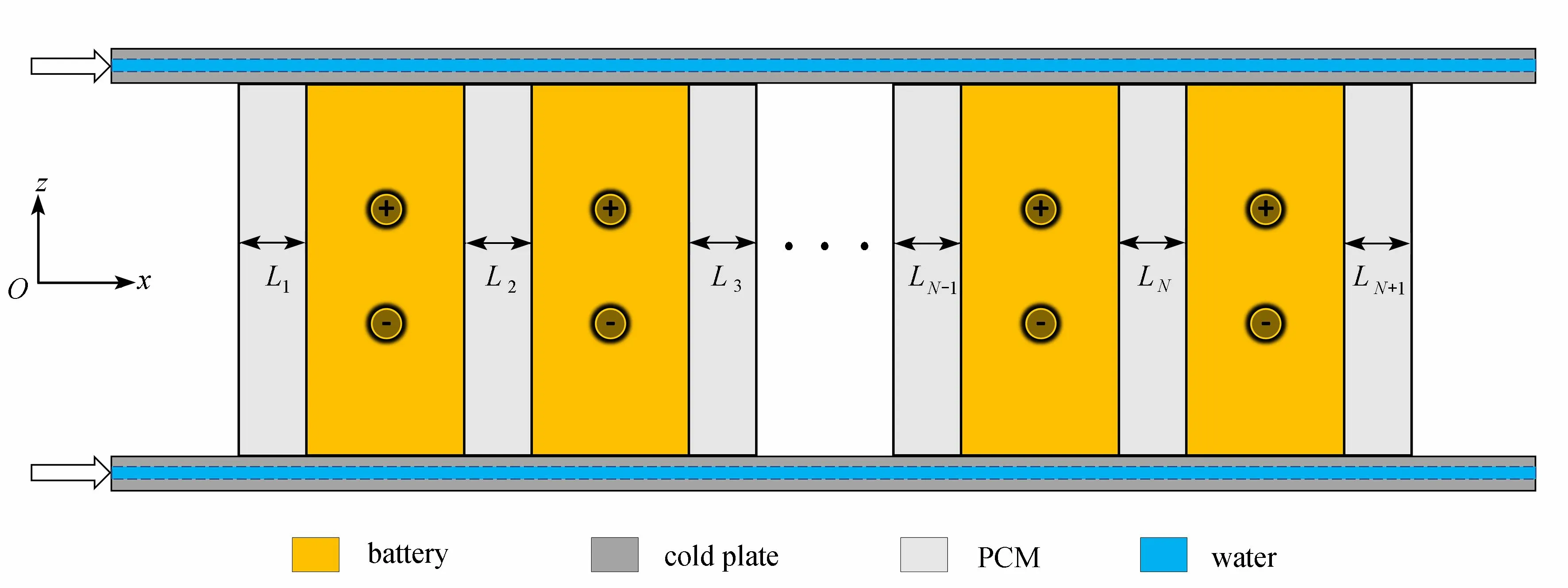
圖4 相變材料耦合冷板系統的主視圖Fig. 4 The main view of the PCM coupled cold plate system

1） 設置相變材料厚度調整步長為ΔL，最小值為Lmin，相變率閾值為 φlim，假設初始時刻電池之間的相變材料厚度相同.

2） 計算耦合系統的溫度場，得到每個電池的平均溫度Tk和電池組溫差ΔT，記錄此時電池間隙分布為最佳分布Lopt，對應的電池組溫差為最佳溫差ΔTopt.

3） 尋找平均溫度最高的電池，標記為i，若i=N，將LN+1增加ΔL；若i≠N，比較第i-1 個電池與第i+ 1 個電池的平均溫度Ti-1和Ti+1，若Ti-1≥Ti+1，將Li增加ΔL，若Ti-1＜Ti+1，將Li+1增加ΔL；若所選相變材料調整區域的相變率低于 φlim，則該區域不作為調整區域，此時尋找平均溫度次高的電池作為參考依據，將其標記為i，按照調整方法繼續調整.

4） 尋找平均溫度最低的電池，標記為j，若j=1，將L1減少ΔL；若j≠1，比較第j-1 個電池與第j+ 1 個電池的平均溫度Tj-1和Tj+1，若Tj-1≤Tj+1，將Lj減少ΔL，若Tj-1＞Tj+1，將Lj+1減少ΔL；若所選相變材料調整區域達到厚度最小值Lmin，則該區域不作為調整區域，此時尋找平均溫度次低的電池作為參考依據，將其標記為j，按照調整方法繼續調整.

5） 再次計算當前系統中每個電池的平均溫度及電池組溫差ΔT，若ΔT＜ ΔTopt，則將當前相變材料分布記為最佳分布Lopt，將當前溫差記為最佳溫差ΔTopt；回到步驟3），重復上述過程，直到ΔT不隨調整步數增加而減小.此時優化過程結束，當前相變材料分布為優化結果.

4 優化結果分析

采用上述優化策略對第2 節的耦合系統進行厚度分布調整.其中，相變材料的初始分布為L=[2，4，4，4，4，4，4，4，2] mm，ΔL，Lmin和 φlim分別設為2 mm，2 mm 和20%.圖5 給出了優化系統溫度特性.電池組Tmax和ΔT隨相變材料厚度調整次數的變化規律如圖5(a)所示.可以看到，隨著調整次數的增加，電池組Tmax和ΔT先逐漸減小，到達最小值后逐漸增加；當調整次數為5 次時，ΔT達到最小值，此時對應的相變材料厚度優化分布為Lopt=[2，2，2，2，2，2，4，10，6] mm.

圖5 優化系統溫度特性：(a)電池組Tmax 和ΔT 隨調整次數的變化；(b)優化前后電池溫度的比較Fig. 5 Temperature characteristics of the optimized system: (a) changes of Tmax and ΔT of the battery pack with adjustment steps;(b) battery temperatures before and after optimization

采用數值方法評估優化后系統的性能，得到放電結束后優化系統的對稱面計算域溫度云圖，如圖6(a)所示.可以看出，與優化前系統相比，優化后下游的相變材料厚度增大，彌補了因下游冷卻水溫度升高造成的冷卻能力下降的問題，因此下游高溫區域有所減少，電池組溫度分布更加均勻（圖5(b)）.圖6(b)顯示了放電結束后優化系統對稱面1 的相變材料液相分數（相變率）云圖.可以看出，相比于優化前系統（圖2(b)），優化后上游的相變材料熔化率上升，下游的相變材料熔化率下降，沿冷卻水流動方向的各相變材料熔化比例更加接近，使相變材料的潛熱得到更充分的利用，而上下游相變材料熔化率差異的減小有利于提升系統的溫控性能.放電結束時，優化系統中電池組Tmax和ΔT分別為321.4 K 和3.5 K，相比優化前系統分別減小了1.1 K 和29%.由圖3(a)可知，優化前系統要保證放電結束時電池組ΔT為3.5 K，冷卻水流量需要由5 g/s 增大到8 g/s，此時冷板功耗由0.023 4 W 增加到0.065 0 W.因此，采用優化策略對相變材料厚度分布進行優化后，在同等冷卻性能下，優化系統的功耗可以降低64%.

圖6 優化系統對稱面1 的計算結果：(a)溫度云圖；(b)相變率云圖Fig. 6 Numerical results of symmetry 1 in the optimized system: (a) the temperature nephogram; (b) the liquid fraction nephogram

5 結 論

本文針對相變材料耦合冷板熱電池管理系統，采用數值方法研究了系統的冷卻性能以及進口流量的影響規律；進一步采用一種優化策略對系統中相變材料的厚度分布進行了調整.通過研究，主要得到了以下結論：優化策略可在較少調整步數情況下得到優化的相變材料厚度分布；典型算例結果表明，相比于優化前耦合系統，優化后電池組Tmax減小了1.1 K，ΔT減小了29%；在同等冷卻能力情況下，優化后系統所需的功耗減小了64%.采用的厚度優化策略為相變材料耦合冷板電池熱管理系統的設計提供了有效指導.

參考文獻（ References ） ：

［1］LU L, HAN X, LI J, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J].Journal of Power Sources, 2013, 226: 272-288.

［2］SAECHAN P, DHUCHAKALLAYA I. Numerical investigation of air cooling system for a densely packed battery to enhance the cooling performance through cell arrangement strategy[J].International Journal of Energy Research, 2021, 49（14）: 20670-20684.

［3］DING Y, WEI M, LIU R. Channel parameters for the temperature distribution of a battery thermal management system with liquid cooling[J].Applied Thermal Engineering, 2021, 186: 116494.

［4］HUANG Y H, CHENG W L, ZHAO R. Thermal management of Li-ion battery pack with the application of flexible form-stable composite phase change materials[J].Energy Conversion and Management, 2019, 182: 9-20.

［5］VUDATA S P, BHATTACHARYYA D. Thermal management of a high temperature sodium sulphur battery stack[J].International Journal of Heat and Mass Transfer, 2021, 181: 122025.

［6］JIANG Z Y, QU Z G. Lithium-ion battery thermal management using heat pipe and phase change material during discharge-charge cycle: a comprehensive numerical study[J].Applied Energy, 2019, 242: 378-392.

［7］LING Z Y, WANG F X, FANG X M, et al. A hybrid thermal management system for lithium-ion batteries combining phase change materials with forced-air cooling[J].Applied Energy, 2015, 148: 403-409.

［8］SONG L, ZHANG H, YANG C. Thermal analysis of conjugated cooling configurations using phase change material and liquid cooling techniques for a battery module[J].International Journal of Heat and Mass Transfer, 2019,133: 827-841.

［9］ 喻寰. 相變材料與液冷耦合的鋰電池熱管理系統研究[D]. 碩士學位論文. 長沙: 湖南大學, 2019. （YU Huan. Study on lithium battery thermal management system based on coupling of phase change materials and liquid cooling[D]. Master Thesis. Changsha: Hunan University, 2019. （in Chinese））

［10］CAO J, LUO M, FANG X, et al. Liquid cooling with phase change materials for cylindrical Li-ion batteries: an experimental and numerical study[J].Energy, 2020, 191: 116565.

［11］LIU Z, HUANG J, CAO M, et al. Experimental study on the thermal management of batteries based on the coupling of composite phase change materials and liquid cooling[J].Applied Thermal Engineering, 2021, 185:116415.

［12］BAI F, CHEN M, SONG W, et al. Thermal management performances of PCM/water cooling-plate using for lithium-ion battery module based on non-uniform internal heat source[J].Applied Thermal Engineering, 2017,126: 17-27.

［13］ZHU Z, WU X, ZHANG H, et al. Multi-objective optimization of a liquid cooled battery module with collaborative heat dissipation in both axial and radial directions[J].International Journal of Heat and Mass Transfer,2020, 155: 119701.

［14］LI J W, ZHANG H Y. Thermal characteristics of power battery module with composite phase change material and external liquid cooling[J].International Journal of Heat and Mass Transfer, 2020, 156: 119820.

［15］WANG R, LIANG Z, SOURI M, et al. Numerical analysis of lithium-ion battery thermal management system using phase change material assisted by liquid cooling method[J].International Journal of Heat and Mass Transfer, 2022, 183: 122095.

［16］MOLAEIMANESH G R, MIRFALLAH N S M, DAHMARDEH M. Impact of configuration on the performance of a hybrid thermal management system including phase change material and water-cooling channels for Li-ion batteries[J].Applied Thermal Engineering, 2020, 181: 116028.

［17］CAO J, LING Z, FANG X, et al. Delayed liquid cooling strategy with phase change material to achieve high temperature uniformity of Li-ion battery under high-rate discharge[J].Journal of Power Sources, 2020, 450:227673.

［18］CHEN Y, CHEN K, DONG Y, et al. Bidirectional symmetrical parallel mini-channel cold plate for energy efficient cooling of large battery packs[J].Energy, 2022, 242: 122553.

［19］CHEN K, HOU J, SONG M, et al. Design of battery thermal management system based on phase change material and heat pipe[J].Applied Thermal Engineering, 2021, 188: 116665.

［20］CHEN K, CHEN Y, SONG M, et al. Multi-parameter structure design of parallel mini-channel cold plate for battery thermal management[J].International Journal of Energy Research, 2020, 44（6）: 4321-4334.

［21］ 白羽, 方慧靈, 張艷. Oldroyd-B流體繞拉伸楔形體的非穩態滑移流動與傳熱分析[J]. 應用數學和力學, 2022, 43（3）:272-280. （BAI Yu, FANG Huiling, ZHANG Yan. Unsteady slip flow and heat transfer analysis of Oldroyd-B fluid over the stretching wedge[J].Applied Mathematics and Mechanics, 2022, 43（3）: 272-280.（in Chinese））

［22］WU W, WU W, WANG S. Thermal management optimization of a prismatic battery with shape-stabilized phase change material[J].International Journal of Heat and Mass Transfer, 2018, 121: 967-977.

［23］ 彭世彬, 郭瑞, 馮上升, 等. 主動冷卻點陣夾層防熱結構溫度響應計算模型[J]. 應用數學和力學, 2022, 43（5）: 477-489. （PENG Shibin, GUO Rui, FENG Shangsheng, et al. A calculation model for temperature responses of active cooling lattice sandwich structures for thermal protection[J].Applied Mathematics and Mechanics, 2022,43（5）: 477-489.（in Chinese））