具有自然年齡和染病年齡的SIQS傳染病模型的穩定性

王時雯，由守科

(新疆大學 數學與系統科學學院， 烏魯木齊 830017)

0 引言

隔離是切斷傳染病傳播途徑的最直接和有效的措施，對防控SARS、COVID-19等惡性傳染病有重要作用[1-3]。近年來，人們建立了許多帶有隔離的微分方程SIQS傳染病模型，并對這些模型的閾值理論或解的持久性進行了研究[4-9]。 然而，這些模型大多沒有考慮自然年齡和染病年齡因素對傳染病傳播的影響，并不能準確反映乙肝、艾滋病等具有較長染病周期的傳染病的傳播。因此，傳染病模型研究中綜合考慮自然年齡、染病年齡和隔離措施是必要的。

1974年，Hoppensteadt[10]綜合考慮隔離、人口遷移、類年齡因素對傳染病傳播的影響，建立了一類自然年齡和染病年齡并存的SIQR傳染病模型，但由于模型結構復雜，該模型解的閾值問題至今未得到解決。之后，相對簡單的自然年齡和染病年齡結構的SIR、SIQR、SEIS、SEIR等傳染病模型解的適定性得到證明[11-14]，但關于平衡解的閾值理論的研究結果較少。至今，自然年齡和染病年齡結構并存的傳染病模型的閾值理論尚無一般結論，只有一些針對具體模型閾值理論的研究結果[15-16]。

1 模型

根據Kermack和Mckendric的傳染病倉室模型思想[17-18]，文獻[19]中建立的一類自然年齡和染病年齡結構并存的SIS模型增加隔離類人群，將人群分為易感類、染病類和隔離類，并假設傳染病無垂直傳染性，建立如下SIQS傳染病模型：

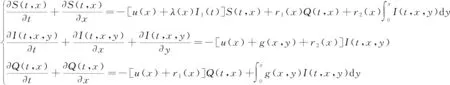
(1)

定解條件為

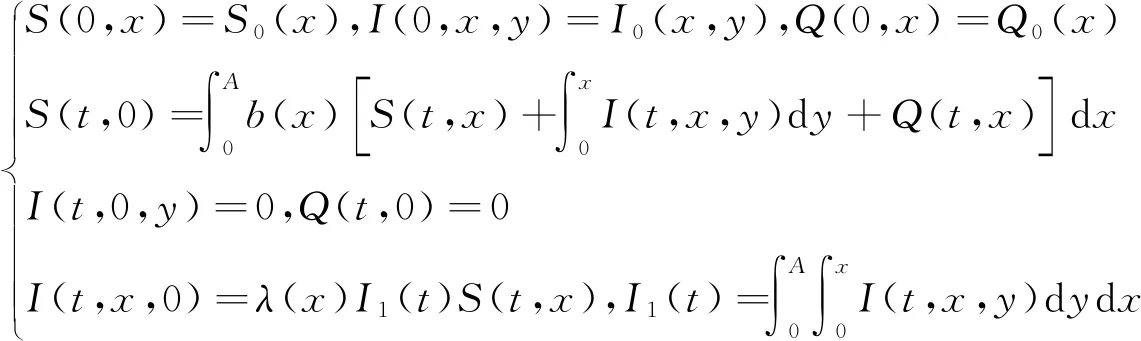
(2)

模型中未知函數S(t,x)、I(t,x,y)、Q(t,x)依次表示易感類、染病類及隔離類人群關于時間t、自然年齡x和染病年齡y的分布密度函數。A為最大年齡，0≤x,y≤A，且y>x時I(t,x,y)=0。參數u(x)、b(x)、λ(x)、g(x,y)依次表示死亡率、出生率、發病率、隔離率函數。r1(x)、r2(x)分別表示隔離類和染病類人群的治愈率函數。S0(x)、I0(x,y)、Q0(x)分別表示3類人群的初始分布密度函數。另外，假設模型中相關函數滿足：

(H1)：S0(x),I0(x,y),Q0(x)在x,y∈[0,A)上是非負連續的有界函數，且S0(x),Q0(x)∈L1((0,A);R)，I0(x,y)∈L1((0,A)×(0,A);R)。

(H2)：r1(x),r2(x),b(x),λ(x),g(x,y)在x,y∈[0,A)上是非負連續的有界函數，u(x)連續且

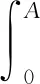
模型(1)和(2)是非線性雙曲方程組，利用壓縮映射原理和先驗估計的標準性方法[20]可以證明非負解的存在性。本文將證明該模型無病平衡解的穩定性和地方病平衡解的存在性。

2 等價模型

聯合模型(1)-(2)得到總人口分布密度函數為

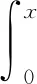
滿足定解問題

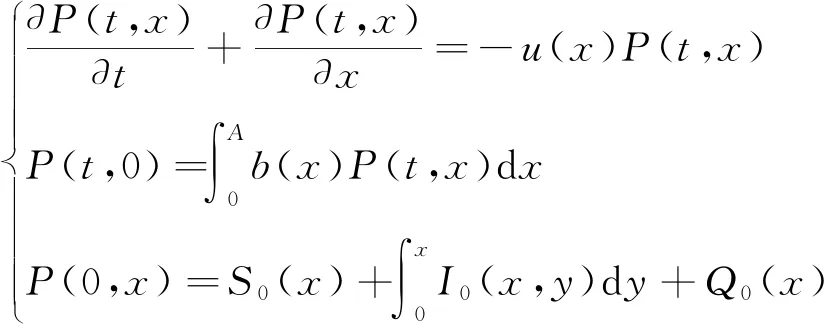
(3)

根據文獻[21]，如果假設

成立，則定解問題(3)存在平衡解

其中

令

S(t,x)=s(t,x)P∞(x),I(t,x,y)=i(t,x,y)P∞(x),Q(t,x)=q(t,x)P∞(x)

代入模型(1)和(2)可得方程

(4)

及定解條件

(5)

其中

從而，對模型(1)和(2)平衡解的研究可歸結為對模型(4)和(5)平衡解的研究。

3 無病平衡解穩定性分析

假設(s*(x),i*(x,y),q*(x))為模型(4)和(5)的平衡解，則

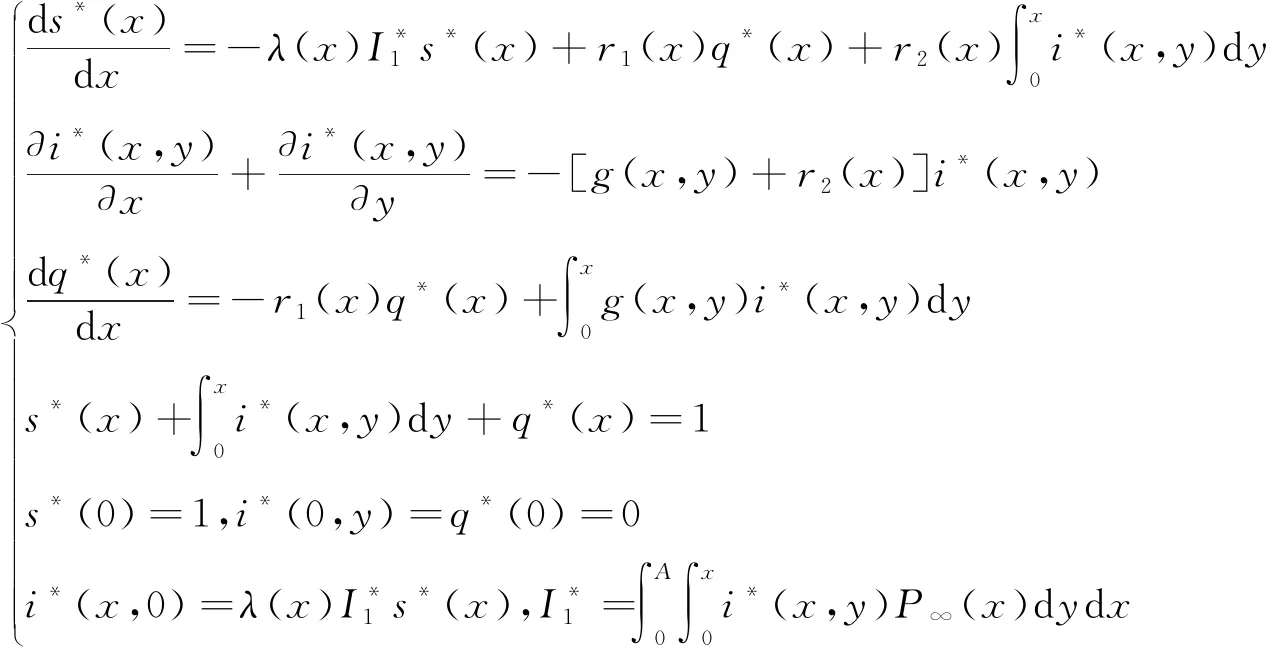
(6)

顯然

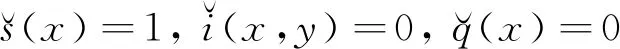
(7)

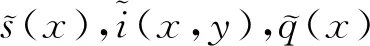
其中

簡單計算可得

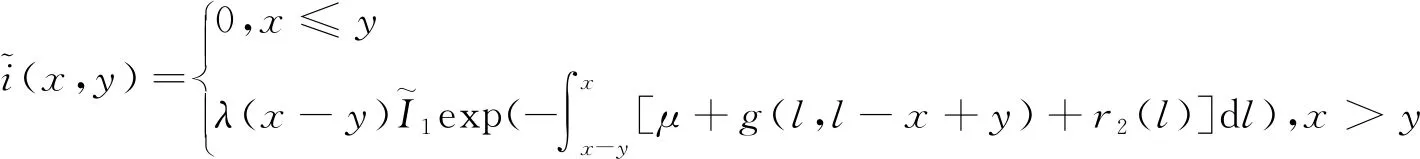
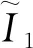
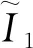
令R=F(0)，即

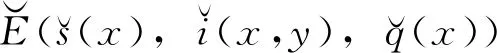
證明令J(μ)=F(μ)-1，則J(μ)為μ的單調遞減連續函數。當R>1時，J(0)=R-1>0，且

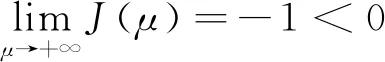
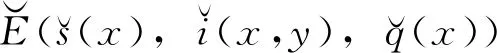
F(μ*)=1=|F(a+ib)|≤F(a)

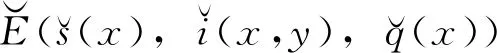
證明利用特征線方法解得模型(4)和(5)的解為

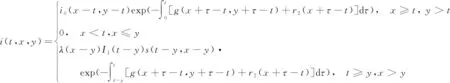
(8)

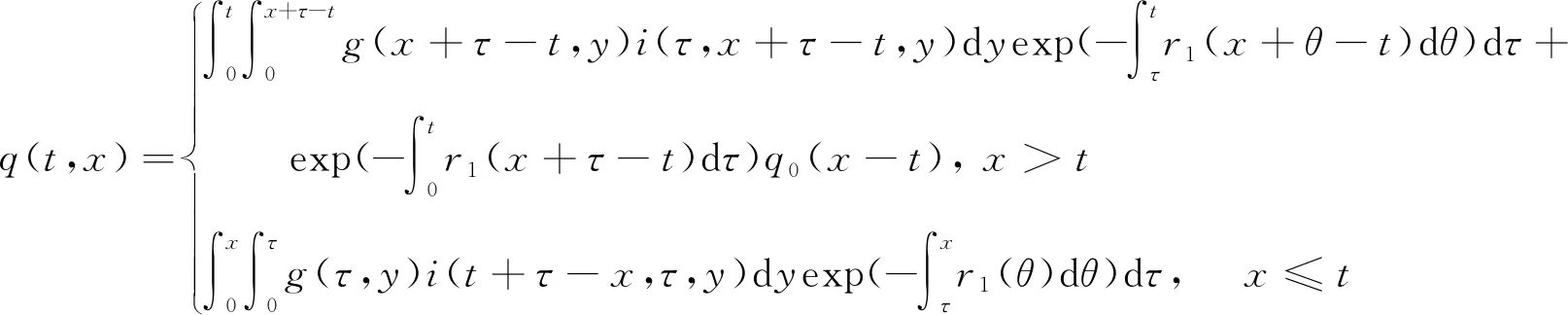
(9)

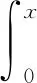
(10)

令h(t,x)=λ(x)I1(t)s(t,x)，由于0≤s(t,x)≤1，故當t>A時

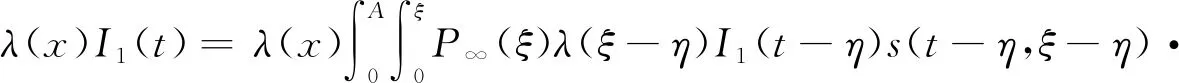
即

(11)

(12)

其中

從而

又因為R<1，則M=0。于是，根據式(12)可得

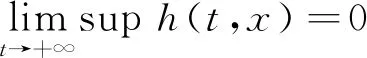
(13)

聯合式(8)—(10)和式(13)得

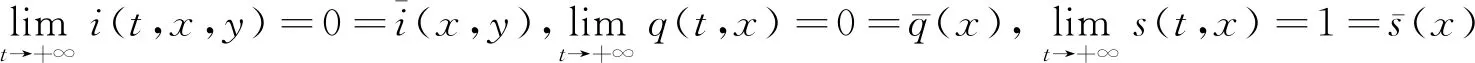
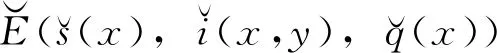
4 地方病平衡解的存在性

當R>1時，受文獻[21-22]的啟發，利用Volterra積分方程理論，可得地方病平衡解存在性定理。

定理3當R>1時，模型(4)和(5)至少存在1個地方病平衡解。

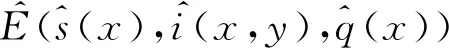
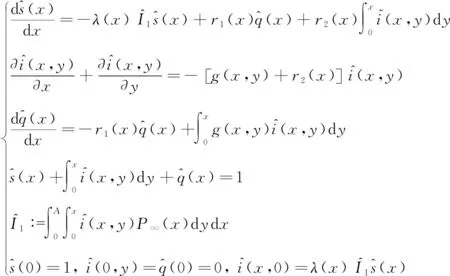
(14)

由式(14)計算得

(15)

(16)

(17)

其中

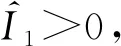
綜上，當R>1時模型(4)和(5)存在地方病平衡解。證畢。

5 結論

討論了一類帶有隔離和染病年齡的SIQS偏微分傳染病模型的閾值理論，得到了閾值R，給出了無病平衡解穩定性和地方病平衡解存在性的條件。從模型的閾值R的表示看，對染病類人群的隔離和治愈是控制疾病傳播的關鍵因素，這在防控SARS和COVID-19疫情中已得到體現。地方病平衡解的唯一性與穩定性問題是后續研究的內容。