2019年揚(yáng)州市中考數(shù)學(xué)壓軸題的解法探究與啟示

張 雪

江蘇省揚(yáng)州市文津中學(xué) 225002

原題呈現(xiàn)

2019年（揚(yáng)州中考·數(shù)學(xué)）第28題：如圖1，已知等邊△ABC的邊長為8，點P是AB邊上的一個動點（與點A，B不重合）.直線l是經(jīng)過點P的一條直線，把△ABC沿直線l折疊，點B的對應(yīng)點是點B′.

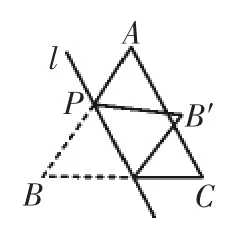
圖1

（1）如圖2，當(dāng)PB=4時，若點B′恰好在AC邊上，則AB′的長度為______；

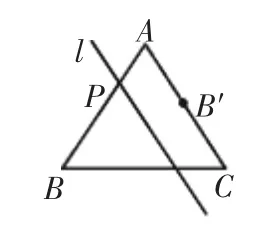
圖2

（2）如圖3，當(dāng)PB=5時，若直線l∥AC，則BB′的長度為______；

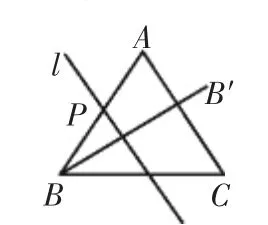
圖3

（3）如圖4，點P在AB邊上運(yùn)動過程中，若直線l始終垂直于AC，△ACB′的面積是否變化？若變化，說明理由；若不變化，求出面積；

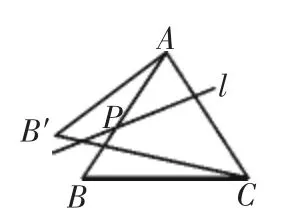
圖4

（4）當(dāng)PB=6時，在直線l變化過程中，求△ACB′面積的最大值.

試題解法探究

（一）對于第（1）問的解法探究

思考方向1：

由題目已知條件可以得到：如圖5，當(dāng)PB=4時，點P是邊AB的中點，由折疊的性質(zhì)可以知道PB=PA=PB′；當(dāng)點B′在邊AC上時，△APB′是等腰三角形，再由△ABC是等邊三角形可知∠A=60°，這樣就可知△APB′是等邊三角形，所以AB′的長度為4.

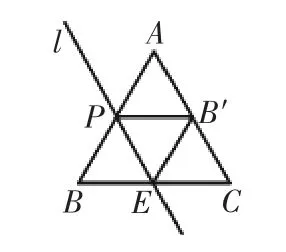
圖5

思考方向2：

由題目已知條件可以得到：如圖6，當(dāng)PB=4時，點P是邊AB的中點，由折疊的性質(zhì)可以知道PB=PA=PB′；因此由圓的集合定義可以知道點A，B，B′在以點P 為圓心，AB 長為直徑的圓上，連接BB′，由直徑所對的圓周角為直角可以知道∠BB′A=90°；再由△ABC是等邊三角形可知∠A=60°，可以知道△BB′A是一個含有60°的直角三角形，由特殊角的三角函數(shù)可以求解AB′=AB=4.

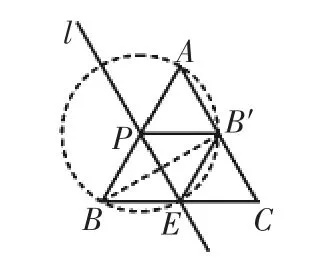
圖6

方法感悟本小題雖是動態(tài)幾何的基礎(chǔ)，但因動點P的位置確定，而轉(zhuǎn)化成了“靜態(tài)”幾何.學(xué)生需要準(zhǔn)確地畫出符合條件的圖形，并依據(jù)軸對稱的性質(zhì)、等邊三角形的性質(zhì)、圓的集合定義、60°角的三角函數(shù)來求解.關(guān)鍵之處是抓住了“折疊出等腰”、借助折疊不變性，如對應(yīng)邊相等、對應(yīng)角相等，實現(xiàn)導(dǎo)角轉(zhuǎn)化，輕松獲解.

（二）對于第（2）問的解法探究

思考方向1：

由l∥AC 可知△BPE∽△BAC，即△ABC與△PBE都是等邊三角形.由折疊不變性可知△PB′E也是等邊三角形，PB=PB′，所以∠BPB′=120°，再由PB=5，頂角為120°的等腰三角形的腰∶底=可得：BB′=5.（如圖7）

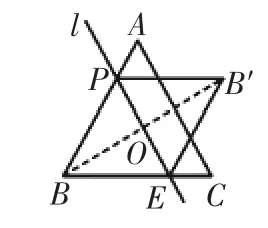
圖7

思考方向2：

如圖7，由“對稱點的連線被折痕垂直平分”可得BB′=2OB.再由l∥AC可知△BPE∽△BAC，即△ABC與△PBE都是等邊三角形，所以∠BPO=60°，結(jié)合PB=5，在Rt△OBP中運(yùn)用60°角的正弦可以求出BO=，所以BB′=5

方法感悟本小題是抓住動直線l與AC平行時，△ABC與△PBE相似，兩個三角形都是等邊三角形.再根據(jù)“折疊不變性” 得到△BPB′是一個頂角為120°的等腰三角形.當(dāng)BP=5長度確定時，根據(jù)“定角定比”巧施比例，直接求解.也可以借助“折疊的性質(zhì)”得到BB′=2OB，當(dāng)BP=5長度確定時，Rt△OBP就是確定的，并通過解直角三角形求解OB，間接求解BB′.學(xué)生抓住了在動點變化中不變的圖形性質(zhì)以及某些變量確定時帶來的新的變量確定，巧妙地定性分析.然后再結(jié)合基本圖形的性質(zhì)來解答，比如含有120°角的等腰三角形底與腰的特殊比、解直角三角形等.

（三）對于第（3）問的解法探究

思考方向：

由本小題條件可知雖然點P位置不確定，但是過點P的直線l始終都滿足：l⊥AC（如圖8）.再由“對稱點的連線被折痕垂直平分”可以得到l⊥BB′，所以BB′∥AC.依據(jù)平行線之間的距離處處相等，再由“同底等高”可知△ACB′面積不變，即S△ACB′=S△ACB=

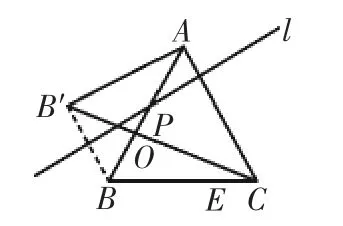
圖8

方法感悟本小題中因為點P的位置不確定，所以過點P的直線l有無數(shù)條.但都滿足l⊥AC，因此直線l是一組互相平行的線，同時點B′隨著直線l 位置的變化而變化，點B′也有無數(shù)個，由“對稱點的連線被折痕垂直平分”可知始終都有：BB′⊥l，所以BB′∥AC，即點B與點B′到AC邊的距離相等，所以學(xué)生會發(fā)現(xiàn)雖然△ACB′的形狀不能確定，但是根據(jù)“同底等高” 可以知道△ACB′面積不變.學(xué)生在思考本小題的解決方法時，可緊扣“變中有恒”，巧妙轉(zhuǎn)化，化未知為已知.

（四）對于第（4）問的解法探究

思考方向：

本題中點P位置確定，BP=6，根據(jù)“折疊不變性” 可得PB′=PB=6.所以根據(jù)圓的集合定義可知：點B′始終在以點P為圓心，6為半徑的定圓上（如圖9）.需要求當(dāng)過點P的直線l在變化過程中，△ACB′面積的最大值，因AC邊長度為8，所以當(dāng)點B′到直線AC的距離最大時，△ACB′面積最大.當(dāng)B′P⊥AC時，垂足為點H，此時距離最大，最大值為B′H（如圖10）.借助于Rt△APH中60°正弦可以求解PH=，所以S△ACB′最大值=

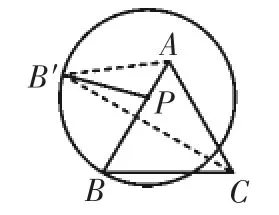
圖9

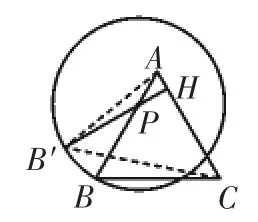
圖10

方法感悟本小題在點P確定的前提下，結(jié)合了點B′的軌跡是圓的思想，及“折疊出隱圓”，從而將問題轉(zhuǎn)化為“在圓上找一點到直線AC的距離最大”.而圓上一點到已知直線的距離最大是圓學(xué)習(xí)中常見的基本圖形，在求解過程中又利用基本圖形——直角三角形，通過三角函數(shù)求解邊的長度.

本考題中涉及動點P、過P點的直線l、定點關(guān)于動直線l的對稱點B′，有三個不確定的量，并且彼此之間有著內(nèi)在的聯(lián)系.第（1）問中確定了點P，B′的位置；第（2）問確定了點P，直線l 的位置都是將“動”變?yōu)椤办o”，利用折疊不變性解決問題；第（3）問直線l隨著點P的運(yùn)動而運(yùn)動，但是始終與邊AC垂直，要求學(xué)生能夠“動中求靜”，分析在變化過程中圖形存在的不變的本質(zhì)性質(zhì)是什么.學(xué)生可以設(shè)想“靜態(tài)”下圖形的特征，研究“靜態(tài)”之下圖形存在的性質(zhì)；第（3）問中抓住了雖然在變化過程中B′的位置不確定，但是BB′與直線l垂直，即BB′始終與AC平行，發(fā)現(xiàn)高不變，進(jìn)而解決問題；第（4）問中點P位置確定但其他都在變化，透過“動態(tài)”現(xiàn)象看本質(zhì)，尋找不變的關(guān)系：PB′=6，可得知點B′的軌跡是圓.再將面積最大值問題轉(zhuǎn)化為點到直線的距離最大.在整個解答過程中，數(shù)學(xué)轉(zhuǎn)化思想被發(fā)揮得淋漓盡致.

幾何教學(xué)啟示

（一）注重夯實基礎(chǔ)，培養(yǎng)學(xué)生運(yùn)用圖形運(yùn)動的思維分析幾何圖形的習(xí)慣

新課標(biāo)提出，注重培養(yǎng)學(xué)生的“四基”：基礎(chǔ)知識、基本技能、基本思想、基本活動經(jīng)驗.

圖形與幾何中的三大圖形變換：圖形平移、旋轉(zhuǎn)、軸對稱（翻折）.在教學(xué)中，既要關(guān)注學(xué)生對這一部分基本知識、基本性質(zhì)的掌握，又要注重培養(yǎng)學(xué)生學(xué)以致用的能力.教師要注重數(shù)學(xué)基本思想和方法在教學(xué)過程中的滲透與梳理，鼓勵學(xué)生大膽嘗試，尋找數(shù)學(xué)本質(zhì)，達(dá)到舉一反三、觸類旁通的學(xué)習(xí)效果.幾何折疊是近幾年中考中的高頻考題，在平時的復(fù)習(xí)教學(xué)中，教師要讓學(xué)生關(guān)注折疊變化、深究折疊本質(zhì)——折疊前后的圖形是全等的，可以導(dǎo)出等角、等邊等結(jié)論.學(xué)生遇到折疊問題時常常會以直角三角形、等腰（邊）三角形、特殊的四邊形、圓等圖形為背景進(jìn)行操作，教學(xué)中教師要注重培養(yǎng)學(xué)生從圖中提煉特殊圖形，并會應(yīng)用特殊圖形的性質(zhì)解決問題的能力，引導(dǎo)學(xué)生注重知識之間的關(guān)聯(lián)，學(xué)會從復(fù)雜圖形中分解出簡單基本的圖形，學(xué)會將復(fù)雜問題簡單化.

（二）關(guān)注專題研究，培養(yǎng)學(xué)生數(shù)學(xué)學(xué)科的核心素養(yǎng)，高效組織中考專題復(fù)習(xí)

數(shù)學(xué)新課標(biāo)倡導(dǎo)積極主動、勇于探索的學(xué)習(xí)方法，注重培養(yǎng)學(xué)生的抽象思維和推理能力，注重培養(yǎng)學(xué)生的創(chuàng)新意識和實踐能力.課程內(nèi)容的呈現(xiàn)應(yīng)注意層次性和多樣性，在平時的中考復(fù)習(xí)教學(xué)過程中多開展“拓展與反思”，讓學(xué)生在經(jīng)歷探究知識的過程中，感悟相關(guān)的數(shù)學(xué)思想，積累數(shù)學(xué)活動經(jīng)驗，從而達(dá)到提高學(xué)生數(shù)學(xué)學(xué)習(xí)能力、培養(yǎng)學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng)這一總目標(biāo).為了避免過度注重數(shù)學(xué)模型的反復(fù)機(jī)械的模仿訓(xùn)練，教師在挑選專題復(fù)習(xí)時，在緊扣教學(xué)大綱的前提下要學(xué)會創(chuàng)造性地使用教材以及各地具有代表性的中考試題等，并進(jìn)行有機(jī)整合，分解題干中的條件和結(jié)論，將零散的條件以問題串的形式出現(xiàn)，讓學(xué)生主動參與、合作探究、歸納總結(jié)，引發(fā)學(xué)生的數(shù)學(xué)思考，給每位學(xué)生足夠的時間和空間進(jìn)行深度思考和學(xué)習(xí)，在時間緊、任務(wù)重的前提下提高中考復(fù)習(xí)的效率.