小學(xué)數(shù)學(xué)“動手操作”教學(xué)路徑

☉宋明珠

伴隨基礎(chǔ)教育改革日益深化，以基本知識、基礎(chǔ)技能為目標的“雙基”教學(xué)正向以基本知識、基本技能、基本思想、基本活動經(jīng)驗為目標的“四基”教學(xué)方向轉(zhuǎn)變。《義務(wù)教育數(shù)學(xué)課程標準（2011年版）》（下簡稱：新課標）指出：數(shù)學(xué)課程不僅要著眼培養(yǎng)學(xué)生掌握必備基礎(chǔ)知識與基本技能，更需要培養(yǎng)學(xué)生抽象思維、推理能力、創(chuàng)新意識、實踐能力等，促進學(xué)生在情感態(tài)度與價值觀等方面發(fā)展。小學(xué)數(shù)學(xué)教學(xué)要從學(xué)生認知規(guī)律出發(fā)，圍繞活動實踐展開教學(xué)設(shè)計，從而有助于促進學(xué)生自主思考與探究，在體驗中加深對數(shù)學(xué)知識理解，最終實現(xiàn)全面提升數(shù)學(xué)核心素養(yǎng)。［1］“動手操作”是小學(xué)階段數(shù)學(xué)教學(xué)的重要方式，借助教具學(xué)具，通過圖形圖表等引導(dǎo)學(xué)生動手操作或參與，將抽象的數(shù)學(xué)知識轉(zhuǎn)化為具體直觀學(xué)習(xí)內(nèi)容。下面從“深度學(xué)習(xí)”角度出發(fā)，談?wù)勑W(xué)數(shù)學(xué)課堂“動手操作”教學(xué)路徑。

一、興趣導(dǎo)入——在“動手操作”中增強數(shù)學(xué)認知

小學(xué)階段數(shù)學(xué)教學(xué)的重要任務(wù)之一，在于喚醒學(xué)生對數(shù)學(xué)的濃郁興趣。深入淺出的教學(xué)設(shè)計，有助于增強學(xué)生的學(xué)習(xí)興趣，喚醒學(xué)生的課堂參與，為進一步深化教學(xué)提供良好教學(xué)基礎(chǔ)。在課堂實踐中，教師要善用“動手操作”教學(xué)設(shè)計，巧借時機為學(xué)生提供動手操作機會，讓其在親身參與中增加對數(shù)學(xué)知識的理解，提升他們的數(shù)學(xué)學(xué)習(xí)興趣。［2］以《認識千克》教學(xué)為例，筆者編排了如下課堂活動，以激發(fā)學(xué)生數(shù)學(xué)興趣。

（一）稱一稱。事先準備一袋標重為1 千克的砂糖，讓同學(xué)們到講臺前用秤稱一下重量，初步感知“千克”數(shù)學(xué)概念。

（二）掂一掂。安排同學(xué)們每人用手掂一掂1 千克砂糖重量，切身體會“千克”實際意義。

（三）估一估。拿出事先準備的橘子，讓學(xué)生掂一掂每個橘子的重量后，估計一下需要幾個橘子才能湊成1 千克，然后稱一稱，驗證學(xué)生的估計。

（四）找一找。將全班同學(xué)分組，要求各組在教室內(nèi)尋找重量與1 千克較為接近的物品，并說一說各組的選擇依據(jù)與理由。

（五）議一議。導(dǎo)入“1 千克棉花重還是1 千克鐵重”話題，引導(dǎo)學(xué)生圍繞其展開討論，讓學(xué)生明白物體重量與物體體積之間沒有直接關(guān)系。

類似課堂設(shè)計有助于引導(dǎo)學(xué)生全程參與，樂在其中，興致盎然。以興趣為導(dǎo)向的“動手操作”教學(xué)活動不僅可以促進學(xué)生對數(shù)學(xué)概念認知與理解，更增強學(xué)生主動探究、自主思考課堂習(xí)慣養(yǎng)成。在“深度學(xué)習(xí)”理念引導(dǎo)下能自覺構(gòu)建起數(shù)學(xué)教與學(xué)之間的親密關(guān)系，便于學(xué)生在數(shù)學(xué)知識與生活經(jīng)驗之間進行良好互動，進一步加深對數(shù)學(xué)知識理解，增強數(shù)學(xué)課程吸引力。

二、情境創(chuàng)設(shè)——在“動手操作”中培養(yǎng)數(shù)學(xué)能力

小學(xué)階段數(shù)學(xué)能力培養(yǎng)涵蓋運算、推理、概括、分析等多個方面。傳統(tǒng)數(shù)學(xué)課堂強調(diào)以教師為主導(dǎo)教學(xué)模式，教師控制著課堂教學(xué)的全部，學(xué)生只是被動參與，成為數(shù)學(xué)知識被動接受者。長此以往，不僅嚴重挫傷了學(xué)生主觀能動性，更對學(xué)生數(shù)學(xué)發(fā)現(xiàn)和提出問題能力、分析和解決問題能力造成嚴重傷害，不利于數(shù)學(xué)能力的生成與發(fā)展。“深度學(xué)習(xí)”強調(diào)新舊知識間的相互交融，主張在新學(xué)內(nèi)容與已有知識中構(gòu)建融洽的教學(xué)情境，以促進學(xué)生主動參與，提升數(shù)學(xué)能力。在教學(xué)實踐中，教師可通過“動手操作”情境介入數(shù)學(xué)課堂，在體驗式教學(xué)中滲透對學(xué)生數(shù)學(xué)能力培養(yǎng)的教學(xué)設(shè)計。以《10 以內(nèi)加法和減法》教學(xué)為例。筆者進行了如下的教學(xué)情境構(gòu)建，通過“動手操作”來促進課堂參與，深化學(xué)生對本課學(xué)習(xí)內(nèi)容理解，并促進學(xué)生數(shù)學(xué)推理能力、分析能力、概括能力提升。讓學(xué)生找出一些數(shù)學(xué)信息。

師：同學(xué)們經(jīng)過之前的學(xué)習(xí)，我們知道了兩個小的數(shù)相加可以得到一個大數(shù)，那么，如果了“1”，以此類推，就把表格填寫完了。

師：很好。大家懂得通過觀察、分析，去探尋問題解決辦法。大家再來試一試，下面這個表格應(yīng)該怎么填？（出示表2，留出時間讓學(xué)生獨立完成）我們將一個大數(shù)，分成兩個小數(shù)，該怎么分呢？（出示表1，留出時間讓學(xué)生獨立完成）

表1 已知大數(shù)情況下的兩個小數(shù)相加

表2 大數(shù)未知情況下的兩個小數(shù)相加

師：哪些同學(xué)完成了？談一談自己填寫的理由。

生1：通過觀察，我發(fā)現(xiàn)8 ＋1 ＝9，所以在表中“8”下面填

生：（按照表1 的內(nèi)容，展開思考，動手填寫）

生：（按照表2 的內(nèi)容，展開思考，動手填寫）

師：哪位同學(xué)可以說一說，表2 該怎么填寫？

生2：我通過表2 中的第8列中的“7”“1”，推斷出這個大數(shù)應(yīng)該是7 ＋1 ＝8，所以，第一列應(yīng)填寫數(shù)字“8”。大數(shù)找到了，下面就好填了。

師：很好。大家通過尋找線索來計算“大數(shù)”具體值，確定了問題中的關(guān)鍵點，接下來所有問題迎刃而解。

……

類似“動手操作”教學(xué)情境的巧妙設(shè)置，促使學(xué)生在數(shù)學(xué)問題解決中獲得深刻體驗，學(xué)生在探究中自覺運用以往的數(shù)學(xué)知識，通過主動思考，將新舊知識完美串聯(lián)，體現(xiàn)了“深度學(xué)習(xí)”理論中“主動”“高投入”“理解”為特征的學(xué)習(xí)行為。學(xué)生在自覺思考、探尋問題解決方法的過程中，不僅促成數(shù)學(xué)知識的深度理解，數(shù)學(xué)能力的提升，而且在問題探究過程中逐漸體會到學(xué)習(xí)成功的喜悅與樂趣，增強了學(xué)習(xí)自信心，品味到了數(shù)學(xué)的無窮魅力。

三、師生互動——在“動手操作”中發(fā)展數(shù)學(xué)思維

小學(xué)數(shù)學(xué)著眼于數(shù)量關(guān)系與空間形式研究，對學(xué)生數(shù)學(xué)思維培養(yǎng)提出了相應(yīng)的教學(xué)要求。新課標將發(fā)展學(xué)生數(shù)感、符號意識、空間觀念、數(shù)據(jù)分析觀念及模型思想等納入課程教學(xué)，體現(xiàn)對學(xué)生數(shù)學(xué)思維能力的全面培養(yǎng)。艾根在其“深度學(xué)習(xí)”理論中提到“充分深度（Sufficient Depth）”觀點，強調(diào)在知識理解中建立學(xué)習(xí)認知方式，以反思學(xué)習(xí)行為，發(fā)展思維品質(zhì)。“動手操作”看似是數(shù)學(xué)教學(xué)的一種方式，實則在教學(xué)中體現(xiàn)對認知資源的融合設(shè)計，意在引導(dǎo)學(xué)生在與學(xué)習(xí)資源充分交流互動中，啟發(fā)批判性思考生成，促進數(shù)學(xué)思維全面提升。以下是筆者在某堂數(shù)學(xué)課上組織的“動手操作”教學(xué)活動。

師：一條大河分南北兩岸，河上沒有橋，行人要靠小船擺渡才能到對岸。現(xiàn)在小船停靠在南岸，擺渡1 次后，就到達了北岸，再擺渡1 次，到達了南岸。請問，擺渡4 次后，小船在南岸還是北岸？擺渡9 次呢？大家能否用畫圖的方式解決這個問題，并告訴我答案。

生：（通過畫圖，很快找到了答案）（詳見圖1）

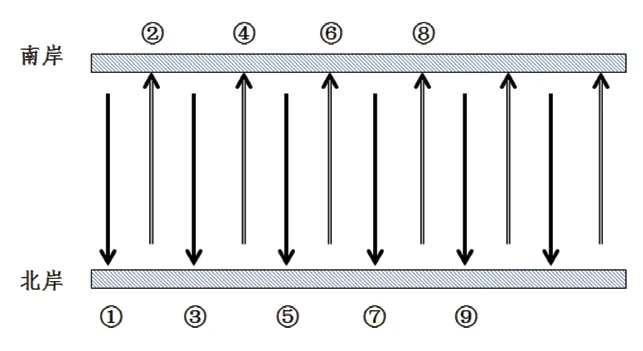
圖1 “動手操作”提升數(shù)學(xué)思維——小船擺渡

師：如果小船擺渡了37 次，船在河的哪個岸邊呢？看看誰先找到正確答案。

生：（有的同學(xué)接著畫圖，有的同學(xué)則在一旁討論。不一會，便有學(xué)生舉手）

生1：是在北岸。

師：為什么呢？

生1：因為往返是2 次，回到原地。37 是18 個往返還余1 次，相當于擺渡1 次。所以在北岸。

師：不錯，很好。其他同學(xué)還有什么不同的解法嗎？

生2：我的答案也是北岸。但我發(fā)現(xiàn)：凡是擺渡次數(shù)是奇數(shù)的，如1，3，5，7 等，都停在北岸，偶數(shù)的，如2、4、6、8 等都停在南岸。37 是奇數(shù)，所以，停在北岸。

師：很好。那么，如果小船擺渡了398 次，請問它最終會停在哪個岸邊？

生：（齊聲）南岸，因為398是偶數(shù)。

通過上述“動手操作”教學(xué)設(shè)計，引導(dǎo)學(xué)生以畫圖方式解決數(shù)學(xué)問題的思維方式，滲透對“數(shù)形結(jié)合”數(shù)學(xué)思維的啟發(fā)。而通過具體畫圖行為（形象思維）來解決簡單數(shù)學(xué)問題，到借助分析概括（抽象思維）來解決復(fù)雜數(shù)學(xué)問題，體現(xiàn)了思維的跨越，有助于引導(dǎo)學(xué)生在學(xué)習(xí)中反思，不斷深化數(shù)學(xué)認知，促進數(shù)學(xué)思維的“充分深度”發(fā)展。

四、加強引導(dǎo)——在“動手操作”中促進數(shù)學(xué)應(yīng)用

小學(xué)階段的數(shù)學(xué)應(yīng)用核心在“問題解決”能力培養(yǎng)，“動手操作”讓學(xué)生從實踐角度發(fā)現(xiàn)問題及提出問題，并借助數(shù)學(xué)知識的綜合運用，有能力解決數(shù)學(xué)問題，從而增強了學(xué)生的應(yīng)用意識，促進創(chuàng)新思維養(yǎng)成。［3］在此過程中，教師不僅是課堂教學(xué)活動的設(shè)計者，更應(yīng)做好學(xué)生自主探究的支持者，全程參與學(xué)生動手環(huán)節(jié)，鼓勵和引導(dǎo)學(xué)生在“動手操作”中提升數(shù)學(xué)能力，完善邏輯思維體系，深層體會數(shù)學(xué)應(yīng)用的無窮魅力。以《分數(shù)的加法》教學(xué)為例，筆者進行了如下教學(xué)設(shè)計。

師：大家來看這道數(shù)學(xué)題，能有什么方法解決？

生1：可以利用通分，將分式中的6 個分數(shù)的分母全部換成64，分式變?yōu)椋?/p>

然后分母不變，分子相加，得出結(jié)果：63/64。

師：很好，還有其他方法嗎？生2：可將上面的分式，進行轉(zhuǎn)化，形成如下算式：

前后抵消，最終分式化簡為1－1/64，結(jié)果為63/64。

師：很好。該同學(xué)通過觀察分數(shù)之間、分母之間內(nèi)在規(guī)律，察覺到后一個分數(shù)恰好等于前兩個分數(shù)相減的結(jié)果，以相互抵消的巧妙方式，簡化了常規(guī)通分計算步驟，簡便了計算過程。還有其他方法嗎？

生：（思考中）

師：請大家拿出一張A4 紙，先對折，然后沿著折痕剪（撕）下來。然后，其中一份留在一邊（1/2），將另一份對折，沿著折痕剪（撕）下來；還是將其中一份放一邊（1/4），將另一份對折裁剪；再將其中一份放一邊（1/8），另一份裁剪；將裁剪后的兩份再留一份（1/16），最后將其中另一份對折裁剪；得到的兩份中其中一份放一邊（1/64），另一份放在自己口袋里。大家桌面上，現(xiàn)在有多少張紙片？

生：6 張。

師：每一張是原先A4 紙的幾分之幾？請寫在紙片上。

生：（按照紙張大小，依次在每張紙片上寫上1/2、1/4、1/8、1/16、1/32、1/64）。

師：把這6 張紙片組合起來，看看是什么情況？

生：（組合后，見圖2）少了一角。

圖2 “動手操作”發(fā)展數(shù)學(xué)應(yīng)用——折紙與運算

師：組合的過程，如果用數(shù)學(xué)計算來理解的話，是什么關(guān)系？

生：相加。

師：那么，剛才組合過程，用算式表達是什么？

生：是將6 個分數(shù)進行相加，即：

師：缺的那個角，大小是多少？

生：1/64。

師：所以，上述分數(shù)相加之后的結(jié)果是什么？

生：1－1/64 ＝63/64。

綜上所述，“動手操作”有助于增強課堂趣味性與參與度，增強學(xué)生對數(shù)學(xué)知識結(jié)構(gòu)的構(gòu)建，形成良好的數(shù)學(xué)思維。“動手操作”教學(xué)設(shè)計要以“深度學(xué)習(xí)”為旨來靈活展開，在此過程中教師要進行積極引導(dǎo)，圍繞學(xué)習(xí)主體設(shè)定，以多樣化教學(xué)形式組織教學(xué)，以充分發(fā)掘?qū)W生學(xué)習(xí)的主觀能動性，促進數(shù)學(xué)深層學(xué)習(xí)意識養(yǎng)成，在充分提升數(shù)學(xué)素養(yǎng)的同時，實現(xiàn)“四基”教學(xué)目標的達成。